薄壳结构的向量式有限元屈曲行为分析

王震，赵阳，杨学林



薄壳结构的向量式有限元屈曲行为分析

王震1, 2，赵阳1，杨学林2

(1. 浙江大学空间结构研究中心，浙江杭州，310058；2. 浙江省建筑设计研究院，浙江杭州，310006)

基于向量式有限元三角形薄壳单元的基本理论，推导力控制法和位移控制法的基本原理及在向量式有限元中的处理方式，以实现薄壳结构的屈曲和后屈曲行为分析。在此基础上编制薄壳结构的屈曲计算分析程序，并通过算例验证。研究结果表明：所编制的向量式有限元薄壳单元程序可以用于薄壳结构的静、动力屈曲和后屈曲分析，验证了理论推导和所编制程序的有效性和正确性。无需进行特殊处理，采用位移控制法可有效越过屈曲极值点，跟踪获得薄壳结构大位移大转动、屈曲及后屈曲运动变形的全过程。

薄壳结构；向量式有限元；三角形薄壳单元；屈曲和后屈曲；位移控制；力控制

屈曲和后屈曲是薄壳结构分析中的一类典型问题，即研究薄壳结构在外荷载作用下产生变形以至丧失原有平衡和承载能力的过程，常伴随有极强的几何非线性效应。目前对于规则形状薄壳结构的屈曲问题已有较多的理论研究成果[1−2]。根据结构失稳时平衡状态的变化特征可分为分枝点失稳和极值点失稳，根据加载特性又可分为静力失稳和动力失稳；传统有限元中用于薄壳结构失稳全过程跟踪分析的主要方法有力控制法、位移控制法和弧长法。ALAMATIAN[3]基于位移增量控制方式并结合动力松弛方法，可获得精确的结构屈曲荷载和后屈曲行为，数值分析表明其具有较好的收敛速度和计算精度。刘正兴等[4]提出交替使用载荷、位移参数确定屈曲路径、临界荷载的数值分析方法，避免了一般方法中存在的极值点处刚度矩阵奇异性的影响。LEE等[5]在结构屈曲路径的预测和校正2个步骤同时引入隐式和显式的Newton−Raphson算法，提出了改进的隐−显和显−隐混合弧长法，并跟踪获得半刚性弹塑性空间框架的后屈曲平衡路径。ZHOU等[6]通过将不平衡荷载向量分解成2个正交向量提出了修正的弧长法，并推导新的约束方程来求解获得当前荷载步长因子，解决了结构屈曲和材料软化的非线性分析。梁珂等[7]基于Koiter的初始后屈曲理论和Newton法的增量迭代技术，通过在降阶模型中引入摄动载荷和主路径上的变形位移，提出能够在非线性屈曲平衡路径上的任意位置展开摄动求解从而实现自动跟踪的降阶方法。向量式有限元(vector form intrinsic finite element，VFIFE)[8−10]以点值描述和向量力学理论为基础，通过牛顿第二定律描述质点运动过程来获得结构的变形和应力。该理论本身不存在几何线性和非线性的区分，克服了传统有限元中容易产生的刚度矩阵奇异和非线性方程迭代不收敛问题，适用于结构大位移大转动、机构运动及复杂结构不连续行为预测分析。对于结构屈曲问题，利用中央差分数值求解质点牛顿运动方程时，无需进行特殊处理即可越过极值点，通过结构构形的步步更新来跟踪获得其屈曲和后屈曲行为。本文作者基于向量式有限元三角形薄壳单元基本理论，分别采用力控制法和位移控制法来跟踪获得薄壳结构屈曲和后屈曲变形的全过程；在此基础上编制薄壳结构屈曲计算分析程序，通过静力和动力屈曲算例分析验证理论推导和所编制程序的有效性和正确性，并对这2种控制方法的特点及其应用范围进行探讨。

1 向量式有限元薄壳单元基本理论

向量式有限元中结构质量集中于质点上，质点间则为无质量的单元连接，本文所用三角形薄壳单元为三角形CST薄膜单元和三角形DKT薄板单元的线性叠加组成。质点运动满足平动微分方程和转动微分 方程：

式中：和分别为质点的质量矩阵和惯量矩阵；和分别为线位移和角位移向量；为阻尼参数；和分别为质点合力和合力矩向量，下标ext和int分别表示外力(矩)和内 力(矩)。

通过中央差分数值求解质点运动式(1)时，需将其转化为差分形式。

连续时，差分形式为

不连续时，差分形式为

式中：Δ为时间步长，−1=1/，，。

以下给出向量式有限元三角形薄壳单元的主要求解过程，详细推导可参考文献[11]。

1.1 单元节点纯变形线(角)位移计算

采用逆向运动方法扣除单元节点全位移中的刚体平移和刚体转动，从而获得节点纯变形线(角)位移，如式(4)所示。刚体平移可取一参考节点的总位移；刚体转动包括面外和面内转动，可通过单元面外(内)刚体转动向量和对应面外(内)逆向转动矩阵来换算获得。对于三角形薄壳单元，质点位移的合并和分离为：变形坐标系下单元面内的节点线位移分量作为膜元部分的位移分量，面外节点线位移和角位移分量作为板元部分的位移分量。

1.2 单元节点内力(矩)计算

基于薄壳单元的变形虚功方程，由单元节点纯变形线(角)位移求解单元节点内力(矩)，如式(5)所示。引入单元变形坐标系和传统有限元单元形函数，在单元平面上求解单元节点内力(矩)向量；通过坐标转换和面外(内)正向转动矩阵，进而转换为整体坐标系下内力(矩)向量；最后反向作用于质点上并进行集成即得到单元传给质点的内力(矩)向量。对于三角形薄壳单元，质点内力的合并和分离为：节点线位移和用于膜元部分的节点内力计算，节点角位移和用于板元部分的节点内力计算。

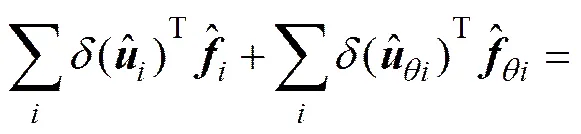
1.3 应力应变转换计算

仅当对结构应力、应变进行输出时才需进行应力应变转换计算，如式(6)所示。对于每个时间步，应力增量均是基于各自不同的变形坐标系下获得，因而上一步末变形坐标系下应力需通过坐标转换矩阵和面外(内)正向转动矩阵，转换到整体坐标系下，再转换到下一步初变形坐标系下，以实现应力的逐步循环计算。对于三角形薄壳单元，需根据膜元部分和板元部分的应力应变性质进行应力应变的合并和分离。

2 力控制法和位移控制法的处理

力控制法和位移控制法是跟踪获得薄壳结构屈曲和后屈曲全过程的2种基本方法，以下给出其基本原理及在向量式有限元中的实现方式。

2.1 力控制法

力控制法以力的变化作为自变量，遵循已知结构外力求解位移反应的一般思路。在施加已知变化的外力后，通过求解质点运动式(1)可直接获得外力作用点或其他位置点的位移变化情况，中央差分位移式(2)和(3)即为力控制方程：

2.2 位移控制法

位移控制法以位移的变化作为自变量，与力控制法相反，其遵循已知结构位移求解外力的逆向思路。在结构位移控制点处假设存在支座，施加已知变化的支座位移后，需另外通过式(2)和(3)的逆形式来获得支座反力(即对应外力)，不连续时该逆形式即为位移控制方程：

在每个循环分析步骤中，通过控制位移控制点处支座位移()的逐步增大，求出结构在该分析步的外力()。初始位移增量可取小于单元厚度t的量级(如t/10)以满足单元小变形大变位假定，从而可避免单元纯变形过大而导致的变形计算失真。

3 程序实现及算例分析

在传统有限元中，结构屈曲和后屈曲过程一般会出现大位移、大转动或大应变，求解平衡方程时为考虑变形的影响应以变形后形状为基本构形，即作为几何非线性问题来处理。而向量式有限元方法并不存在几何线性和非线性的区分，在每一时间子步内均为小变形大变位过程，因而均以变形前形状为基本构形，对于结构屈曲问题无需进行特殊处理，采用显式时间积分进行步步更新便可获得结构的应力和变形。

基于向量式有限元三角形薄壳单元基本理论和位移(力)控制处理方法，本文采用Matlab编制了薄壳结构的屈曲计算分析程序，并分别通过静力和动力屈曲算例分析验证理论推导和所编制程序在薄壳结构静力和动力屈曲分析领域的有效性和正确性，程序实现流程如图1所示。

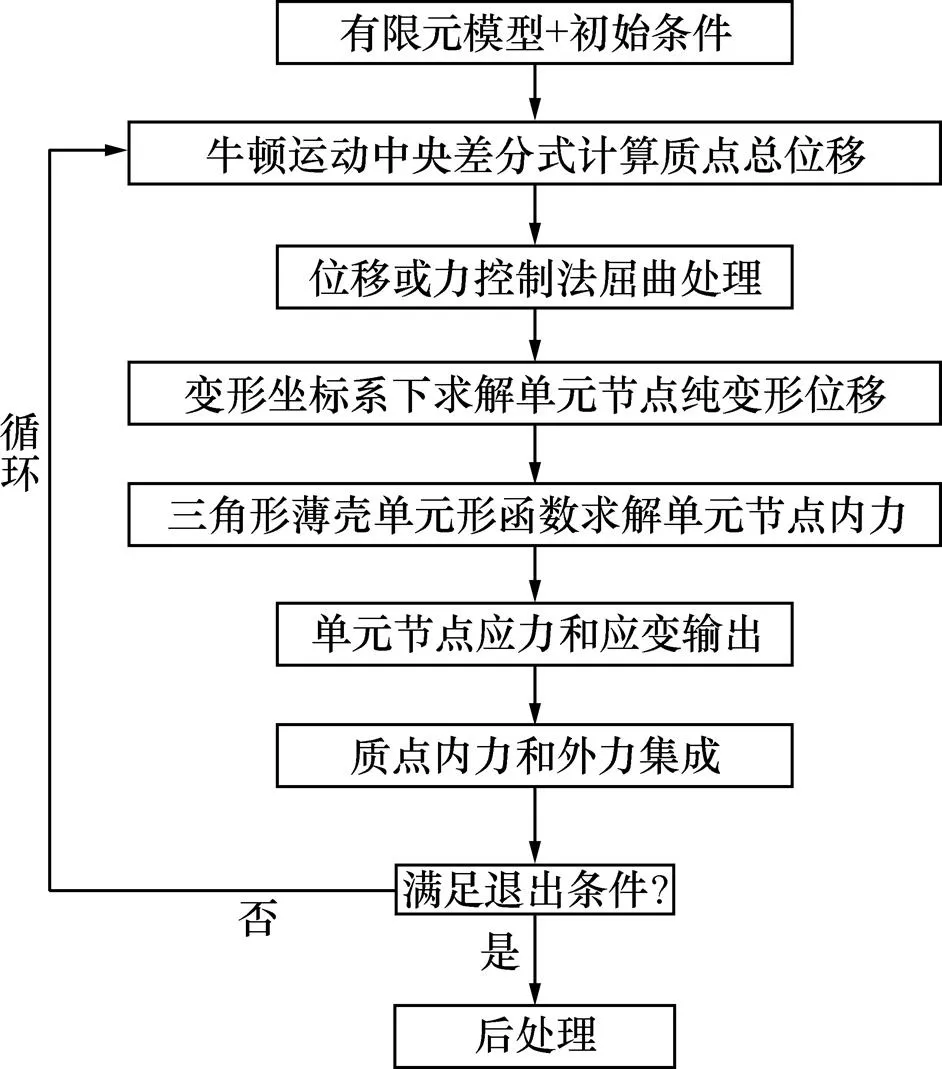
图1 薄壳结构屈曲分析流程图

3.1 柱面壳的静力屈曲分析

两边简支的柱面壳结构是分析跃越失稳问题的经典算例[7, 12]，采用位移控制法和力控制法跟踪薄壳结构屈曲和后屈曲变形的全过程。柱面壳的半径= 2.54 m，两纵向边边长=0.508 m，厚度t=12.7 mm，曲边弧度角为=0.2 rad；初始两纵向边简支、两圆弧曲边自由，中心受竖向集中荷载作用；壳体的弹性模量=3.102 75 GPa，泊松比=0.3，密度=2 500 kg/m3。采用三角形薄壳单元网格，共计200个单元和121个节点，结构模型如图2所示。分析时间步长取=2.0×10−5s，阻尼参数取=36(由文献[13]方法计算获得)。

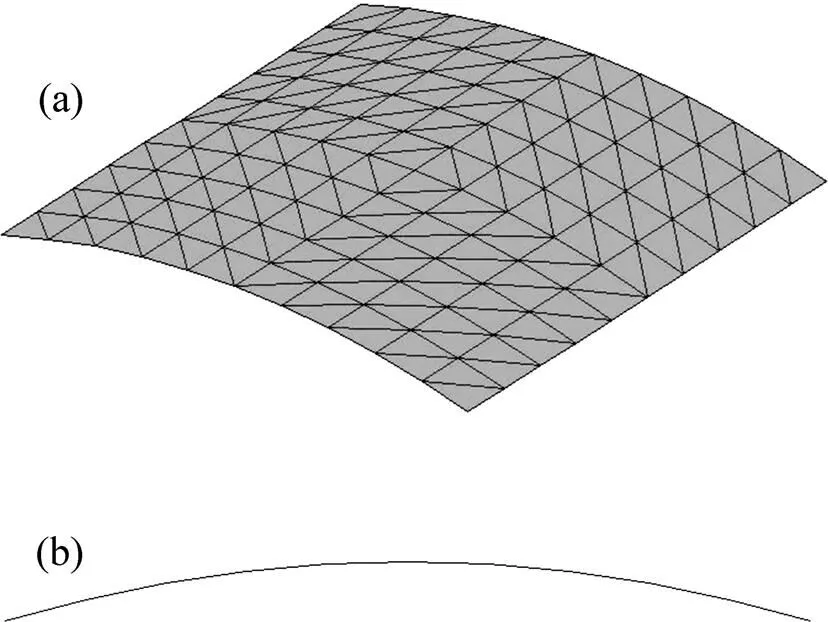
(a) 三维图；(b) 侧视图

图3所示为外荷载随顶部中心节点竖向位移的变化曲线，并与文献[12]结果进行比较。由图3可见：位移控制法结果与文献结果符合较好，成功获得柱面壳大位移大转动、屈曲及后屈曲的全过程变化曲线，包括屈曲前上升段、屈曲后下降段及后屈曲承载上升段；本文方法所获得上、下临界极限荷载分别为2.23 kN和0.53 kN，与文献[12]结果(2.21 kN和0.56 kN)的相对误差仅为0.90%和5.36%。力控制法的屈曲和后屈曲上升段均与文献结果符合，而屈曲后下降段由于荷载的逐步递增施加表现为快速递增跳过(无法获得精确的临界极限荷载)；且跳过下降段后由于该段位移变化过快，在后屈曲上升初始还存在小幅振荡效应。

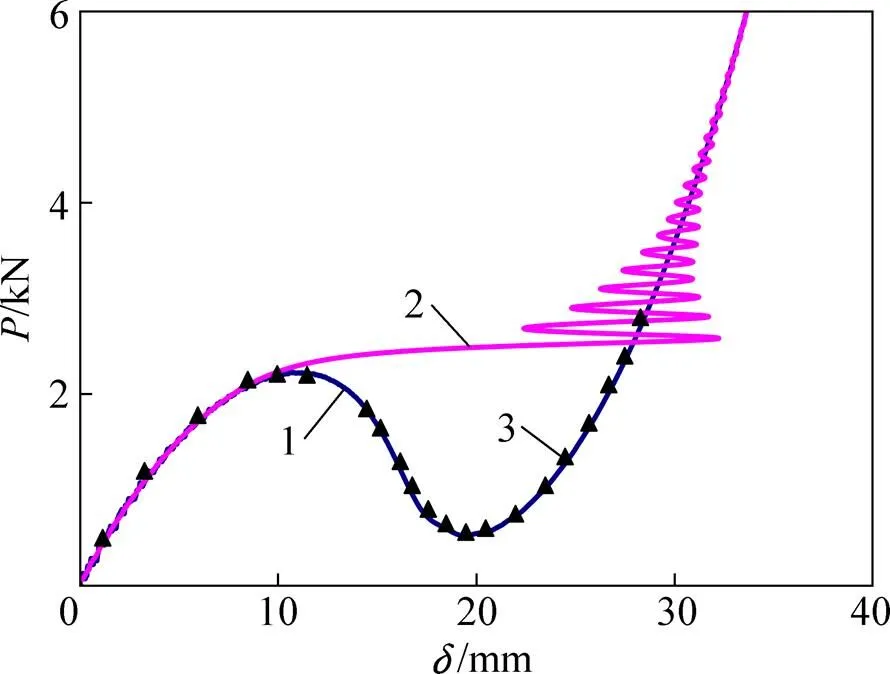
1—位移控制；2—力控制；3—文献[12]结果。

图4所示为几个典型时刻柱面壳屈曲和后屈曲的变形和Mises应力分布云图(Matlab后处理中自行编制程序绘制获得)，以更加直观地观察其应力变化及变形发展情况。可见：随着控制位移的递增施加，柱面壳中心的变形也逐渐增大，位移为10.8 mm时达到极值点而出现屈曲；随后开始发生快速翻转(对应荷载−位移的下降段)，位移为19.4 mm到达下降段的极小值点；之后，柱面壳变形再次缓慢增大(对应后屈曲的上升段)。

中心节点竖向位移/mm：(a) 10.8(屈曲)；(b) 19.4(屈曲后下临界极限)；(c) 25；(d) 30

3.2 圆柱壳的动力屈曲分析

本算例采用位移控制法分析圆柱薄壳结构在轴压荷载作用下的动力屈曲和后屈曲问题[14−15]。圆柱壳的半径=0.1 m，轴向长度=0.5 m，厚度t=2.0 mm，初始底端固定，顶端仅有轴向自由度并按强制性位移控制形式进行加载，使该端截面以40 m/s的速度沿轴向发生压缩位移；壳体的弹性模量=201 GPa，泊松比=0.3，密度=7 850 kg/m3；采用三角形薄壳单元网格，共计2 560个单元和1 320个节点，结构模型如图5所示。分析时间步长取=1.0×10−6s(对应位移增量步长为4.0×10−5 m)，阻尼参数取=0(即不考虑阻尼效应)。

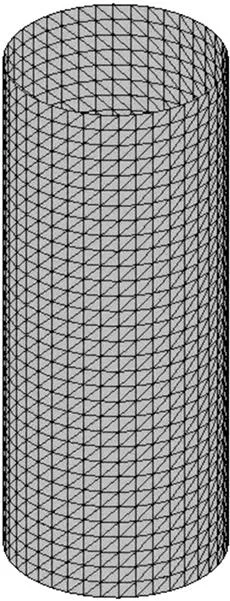
图5 圆柱薄壳模型及其网格划分

图6所示为顶端的总轴压荷载随轴向位移的变化曲线，并与ABAQUS计算结果进行比较。由图6可见：位移控制法的前3次屈曲情况均与ABAQU符合较好；第3次屈曲之后开始出现差异，但总的变化趋势仍基本一致。本文方法获得的前3次屈曲荷载分别为2 286.9，6 125.0和6 888.7 kN，与ABAQUS结果(分别为2 252.7，5 565.0和6 870.1 kN)的相对误差仅为1.50%，9.14%和0.27%；验证了本文方法在薄壳结构动力屈曲分析中的有效性和准确性。

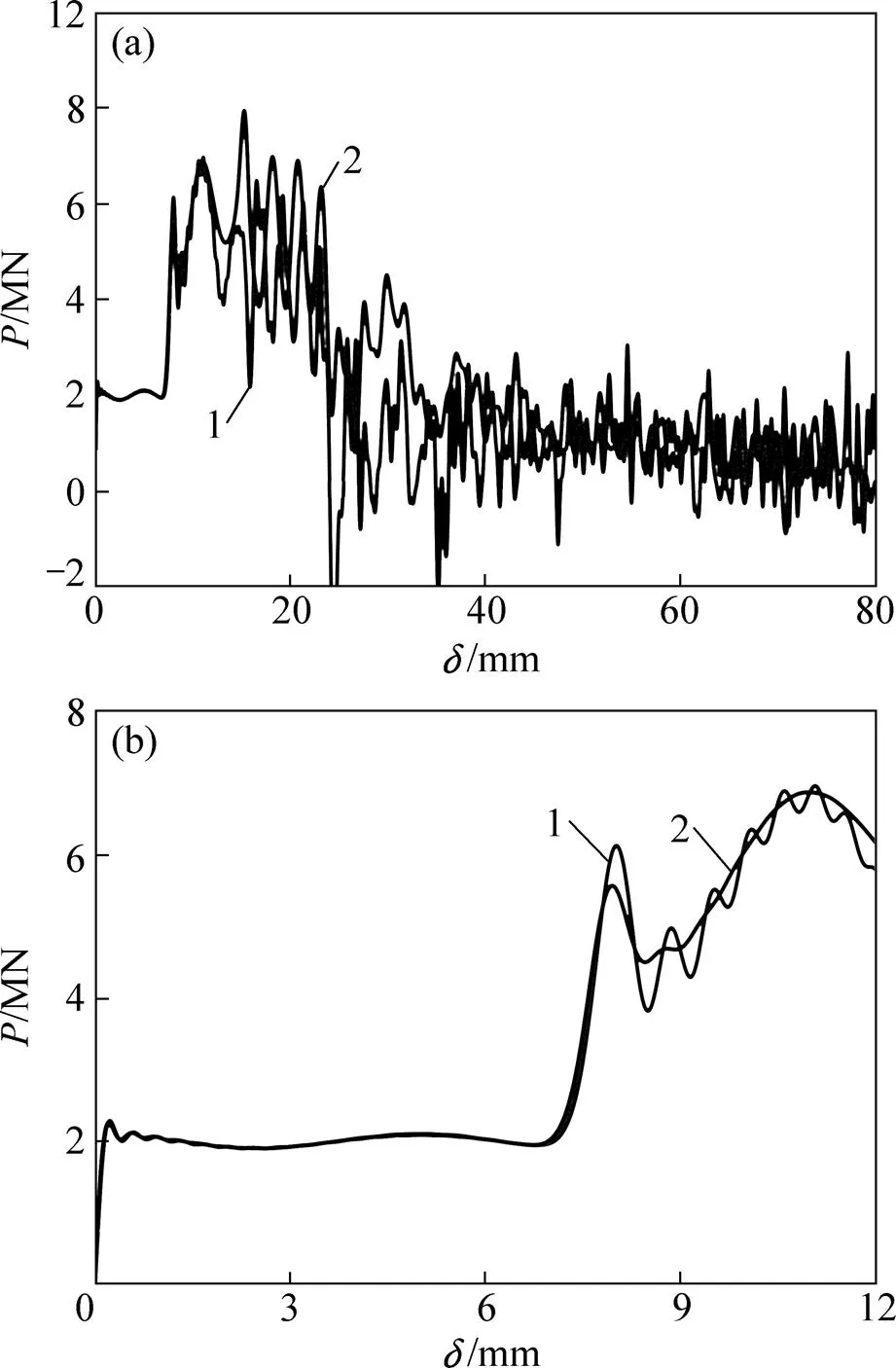
轴向位移/mm：(a) 0~80；(b) 0~12(前3次屈曲)1—位移；2—ABAQUS。

图7所示为几个典型时刻圆柱薄壳屈曲和后屈曲的变形和Mises应力分布云图。由图7可见：随着控制位移的递增施加，首先在柱壳顶端出现局部屈曲(第1次屈曲模态)，接着在柱壳底端出现局部屈曲(第2次屈曲模态)，之后的高阶屈曲则开始逐步扩展至柱壳整体(整体屈曲模态)。

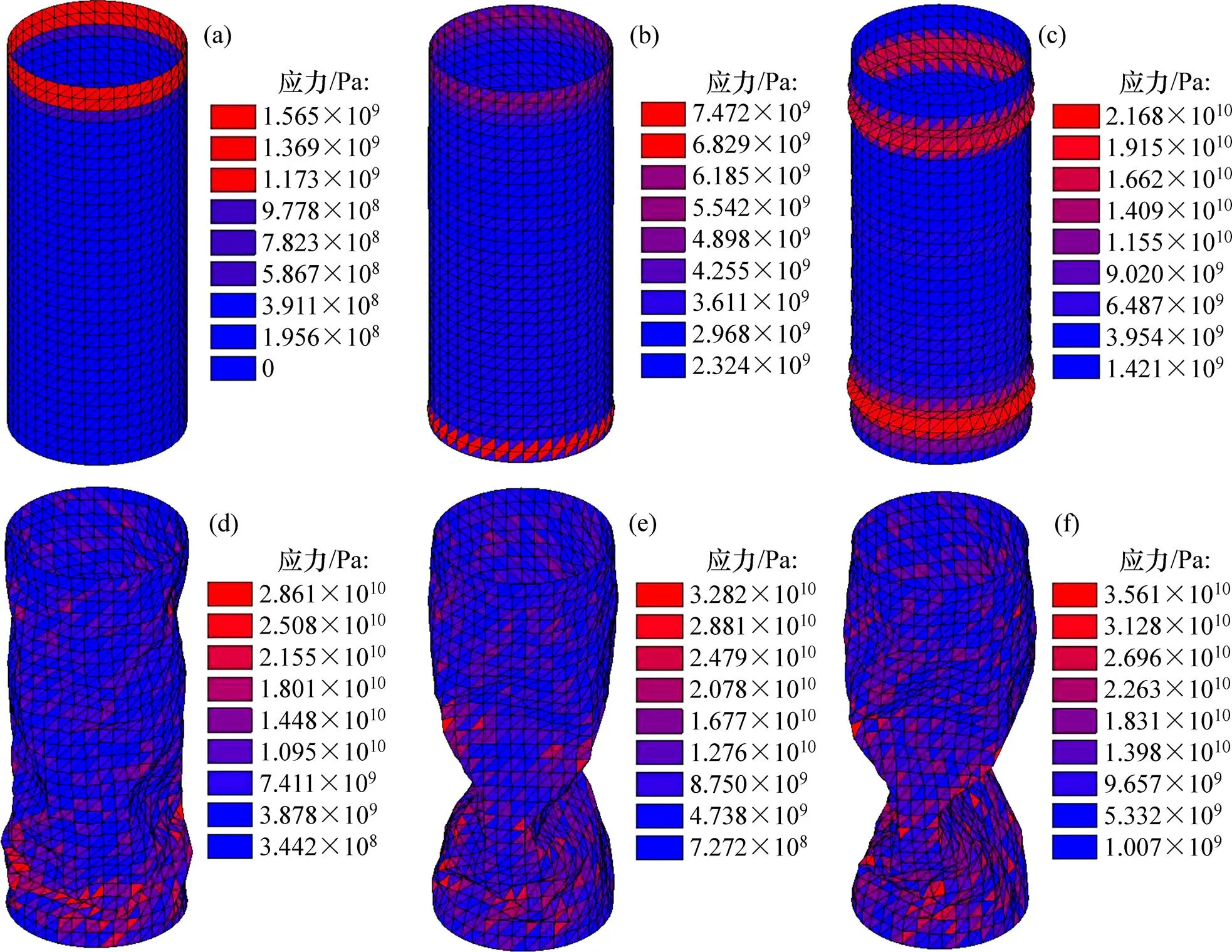
轴向位移/mm：(a) 0.28(第1次屈曲)；(b) 8.04(第2次屈曲)；(c) 20；(d) 40；(e) 60；(f) 80

由于本文向量式有限元方法基于质点动力分析的理论基础，在薄壳结构动力屈曲问题中更为适用；屈曲和后屈曲过程通常伴随有大变形大转动，该法克服了传统有限元中容易产生的刚度矩奇异和非线性方程迭代不收敛问题，通过结构构形的步步更新可轻易跟踪获得其屈曲和后屈曲行为；相对传统有限元计算更为准确和迅速。

4 结论

1) 基于向量式有限元三角形薄壳单元的基本理论，推导了力控制法和位移控制法的基本原理及在向量式有限元中的处理方式，以实现薄壳结构的屈曲和后屈曲行为分析。

2) 编制了薄壳结构屈曲计算分析程序，并进行了算例验证。算例分析表明所编制程序可很好地完成薄壳结构的静、动力屈曲和后屈曲分析，验证了理论推导和所编制程序的有效性和正确性。

3) 采用位移控制法可有效跟踪薄壳结构运动变形的全过程，并获得薄壳结构失稳后的下降段和精确的上、下临界极限荷载；而力控制法无法获得位移的下降段且在后屈曲上升初始会存在小幅度的振荡效应。

4) 当作用位置点同时存在荷载和位移的下降段时，需引入更为高级的弧长法才可获得准确的荷载−位移曲线，本文将进行进一步研究。

[1] TENG J G, ROTTER J M. Buckling of thin metal shells[M]. London: Spon Press, 2004: 1−41.

[2] 沙风焕. 圆柱壳的动力屈曲理论及其应用[M]. 北京: 中国建材工业出版社, 2008: 62−89. SHA Fenghuan. Theory and application of dynamic bucking of cylindrical shells[M]. Beijing: China Building Materials Press, 2008: 62−89.

[3] ALAMATIAN J. Displacement-based methods for calculating the buckling load and tracing the post-buckling regions with dynamic relaxation method[J]. Computer & Structures, 2013, 114: 84−97.

[4] 刘正兴, 叶榕. 薄壳后屈曲分析的载荷−位移交替控制法[J]. 上海交通大学学报, 1990, 24(3): 38−44. LIU Zhengxing, YE Rong. Alternatively controlling technique of load and displacement for post-buckling analysis of thin shells[J]. Journal of Shanghai Jiaotong University, 1990, 24(3): 38−44.

[5] LEE K, HAN S E, HONG J W. Post-buckling analysis of space frames using concept of hybrid arc-length methods[J]. International Journal of Non-linear Mechanics, 2014, 58: 76−88.

[6] ZHOU L Y, LI Q, LI T M, et al. Improved arc-length method for solving buckling problem[J]. Journal of Southwest Jiaotong University, 2011, 46(6): 922−925.

[7] 梁珂, 孙秦, GURDAL Z. 结构非线性屈曲分析的有限元降阶方法[J]. 华南理工大学学报(自然科学版), 2013, 41(2): 105−110. LIANG Ke, SUN Qin, GURDAL Z. Finite element-based order reduction method for nonlinear buckling analysis of structures[J]. Journal of South China University of Technology (Natural Science Edition), 2013, 41(2): 105−110.

[8] TING E C, SHIH C, WANG Y K. Fundamentals of a vector form intrinsic finite element: part I. Basic procedure and a plane frame element[J]. Journal of Mechanics, 2004, 20(2): 113−122.

[9] TING E C, SHIH C, WANG Y K. Fundamentals of a vector form intrinsic finite element: part II. Plane solid elements[J]. Journal of Mechanics, 2004, 20(2): 123−132.

[10] WU T Y, WANG C Y, CHUANG C C, et al. Motion analysis of 3D membrane structures by a vector form intrinsic finite element[J]. Journal of the Chinese Institute of Engineers, 2007, 30(6): 961−976.

[11] 王震, 赵阳, 胡可. 基于向量式有限元的三角形薄壳单元研究[J]. 建筑结构学报, 2014, 35(4): 64−70. WANG Zhen, ZHAO Yang, HU Ke. Triangular thin-shell element based on vector form intrinsic finite element[J]. Journal of Building Structures, 2014, 35(4): 64−70.

[12] HORRIGMOE G, BERGAN P G. Nonlinear analysis of free-form shells by flat finite element[J]. Computer Methods in Applied Mechanics and Engineering, 1978, 16(1): 11−35.

[13] 王震, 赵阳, 胡可. 基于向量式有限元的三角形薄板单元研究[J]. 工程力学, 2014, 31(1): 37−45. WANG Zhen, ZHAO Yang, HU Ke. Triangular thin-plate element based on vector form intrinsic finite element[J]. Engineering Mechanics, 2014, 31(1): 37−45.

[14] 邢小东, 侯飞. 轴向冲击载荷下圆柱壳动力屈曲的计算机仿真[J]. 机械管理开发, 2008, 23(1): 77−78. XING Xiaodong, HOU Fei. The computer simulation on dynamic buckling of cylindrical shells under axial impulsive load[J]. Mechanical Management and Development, 2008, 23(1): 77−78.

[15] 李帅. 冲击载荷下圆柱壳非线性动力屈曲的数值研究[D]. 大连: 大连理工大学化工机械与安全学院, 2005: 46−72. LI Shuai. Numerical research for nonlinear dynamic buckling of shell under axial impacted load[D]. Dalian: Dalian University of Technology. School of Chemical Machinery and Safety Engineering, 2005: 46−72.

(编辑 赵俊)

Vector form intrinsic finite element method for buckling analysis of thin-shell structures

WANG Zhen1, 2, ZHAO Yang1, YANG Xuelin2

(1. Space Structure Research Center, Zhejiang University, Hangzhou 310058, China;2. Zhejiang Province Institute of Architectural Design and Research, Hangzhou, Zhejiang 310006, China)

Based on the basic theory of triangular thin-shell element of VFIFE, the basic principles of force-controlled method and displacement-controlled method were derived, and the corresponding processes of VIFIFE were presented. Then buckling and post buckling behavior for thin-shell structures were analyzed. On this basis, a computer program of the buckling analysis for triangular thin-shell element was developed and numerical examples were provided. The results show that the static and dynamic buckling and post buckling analysis can be well performed for thin-shell structures by the developed program, verifying the validity and the correctness of the theoretical derivation and the computer program. Without special processing, the buckling extreme point can be acrossed effectively by adopting displacement-controlled method, and the whole deformation of large deformation and large rotation, buckling and post buckling of thin-shell structures can be tracked.

thin-shell structures; vector form intrinsic finite element; triangle thin-shell element; buckling and post buckling; displacement-controlled method; force-controlled method

10.11817/j.issn.1672-7207.2016.06.033

TU33

A

1672−7207(2016)06−2058−07

2015−06−15；

2015−09−03

国家自然科学基金资助项目(51378459)(Project(51378459) supported by the National Natural Science Foundation of China)

赵阳，教授，博士生导师，从事薄壳结构、钢结构和向量式有限元研究；E-mail：ceyzhao@zju.edu.cn