任意实小波函数的高阶开关电流滤波器通用实现方法

李目，吴笑峰，席在芳，胡仕刚，李劲，邬书跃



任意实小波函数的高阶开关电流滤波器通用实现方法

李目1，吴笑峰1，席在芳1，胡仕刚1，李劲1，邬书跃2

(1. 湖南科技大学信息与电气工程学院，湖南湘潭，411201；2. 湖南涉外经济学院信息科学与工程学院，湖南长沙，410205)

通过对实小波函数的模拟滤波器实现原理进行分析，将其实现过程分解为实小波函数逼近和小波滤波器设计2步，提出一种适合任意实小波函数的高阶开关电流滤波器通用综合方法，并设计具体的电路模型。首先，基于网络系统综合理论，构建实小波函数的通用优化逼近模型；然后，以开关电流双线性积分器和电流镜为基本单元设计出冲激响应为实小波逼近函数的通用多环反馈结构滤波器，通过调节开关电流滤波器的时钟频率获得不同尺度小波函数。以开关电流实Morlet小波滤波器设计为例验证该通用方法的正确性。

开关电流电路；小波函数；函数逼近；小波滤波器设计

小波分析是20世纪80年代中期迅速发展起来的一门新兴学科，小波变换以其良好的时频局部化特性被广泛地应用于信号处理领域，成为分析非平稳信号最有力的工具之一。随着小波分析理论与算法的进一步发展和工程应用的不断拓展，连续小波变换硬件实现成为应用研究的重要课题。目前，最常见的连续小波变换实现方法是采用数字信号处理器(DSP)或可编程逻辑器件(FPGA)等数字电路完成。采用通用数字器件实现连续小波变换的主要优点是相关技术成熟、通用性和可编程性较好、设计过程比较简单、开发周期短。然而，数字电路实现的连续小波变换在处理模拟信号时需要在系统中增加A/D器件，使系统的功耗、体积和处理速度以及精度受到影响，难以满足低压、低功耗、强实时性和高精度的实际应用需求。研究连续小波变换的模拟电路实现成为当前的主要途径。模拟电路实现连续小波变换的方法主要包括时域法[1−3]和频域法[4−14]。由于时域法中设计产生不同尺度和位移小波簇的小波函数发生器非常困难，所以，频域法成为目前模拟连续小波变换实现的主要方法。因为信号的连续小波变换在频域相当于不同尺度且品质因数恒定的带通滤波器组对信号进行滤波处理，因此，多尺度小波滤波器设计成为频域法实现连续小波变换的关键。国内外学者提出了多种基于连续时间滤波器[4−8]和抽样数据滤波器[9−14]的连续小波变换实现方法。由于连续时间滤波器特性取决于元件参数的绝对值，而精确参数元件难于实现，离散时间滤波器特性取决于元件参数比值或时钟频率，易于实现精确控制，所以，抽样数据滤波器实现连续小波变换成为当前的重要发展方向。EDWARDS等[9−11]提出基于开关电容滤波器的连续小波变换实现方法，但开关电容电路与数字VLSI CMOS工艺不兼容，且该电压模电路与低压高速、大动态范围集成电路发展趋势不相适应，因此，电流模开关电流滤波器实现连续小波变换成为研究热点。胡沁春等[12]提出了基于Padé频域逼近的串联结构开关电流滤波器实现连续小波变换方法，但Padé逼近法中分子分母多项式次数难以确定且不能保证获得的系统是稳定的；赵文山等[13]利用最小二乘法逼近时域实小波函数，采用并联结构开关电流滤波器设计实现连续小波变换，但最小二乘法属于局部优化算法，使该算法收敛至最优的初始值难于选择。同时，以上串、并联结构开关电流滤波器的共同缺点是通带灵敏度高。李目等[14]采用麦克劳林级数逼近实小波频域函数，设计了多环反馈结构开关电流小波滤波器实现连续小波变换，但前提是实小波函数的频域函数存在，缺乏通用性。为此，本文作者在上述开关电流小波滤波器设计的基础上，提出任意时域实小波函数的通用优化逼近模型，并给出高阶多环反馈开关电流小波滤波器通用设计方法。通过对逼近模型阶次的调整，可获得不同逼近精度的小波逼近函数；修改高阶多环反馈开关电流小波滤波器中的前馈和反馈系数，即可设计出任意小波滤波器。

1 实小波函数的通用逼近模型

式中：“*”表示卷积。由式(1)可知：对于函数()在尺度下的连续小波变换可看成是函数()通过脉冲响应为的线性时不变滤波器后的结果，且该滤波器的传递函数应满足

因此：连续小波变换实现转化为脉冲响应为不同尺度和位移小波函数的滤波器组设计。对于常见小波函数，其()通常是非有理和非因果的，由电网络理论可知，该系统是不能直接用电路综合实现，所以，必须构造可综合实现的小波逼近函数。为了使满足因果关系，对其进行合适的时间延迟为，然后对其构建相应的通用逼近模型。

根据线性系统理论可知，严格因果的线性时不变滤波器可以用状态空间系统(，，)描述，其一阶微分方程表达式为

该系统的脉冲响应和频域传递函数为：

分析式(4)可知：在一般情况下，具有不同极点稳定系统的脉冲响应()是衰减指数信号和呈指数衰减谐波信号的线性组合。因此，阶滤波器的冲激响应()的通式可表示为

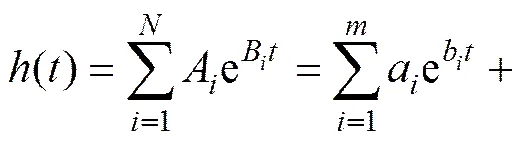
式中：A和B为实数或复数；a，b，c，d，ρ和f为实数；和对应实极点个数，且+=。考虑1个8阶滤波器，其脉冲响应()可表示为

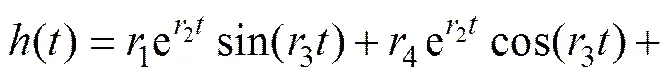
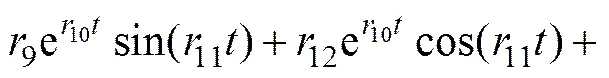
为了保证系统的稳定性，必须满足2＜0，6＜0，10＜0，14＜0。于是，时延小波函数的逼近问题转换为()的系数求解。定义()与的逼近误差平方和为

式(8)的离散型式为

式中：为采样点数；Δ为采样间隔。求()的系数等价于使()达到最小值的有约束条件最优化问题，其通用模型为

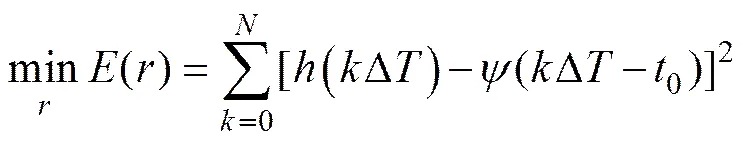
s.t.r＜0；=2，6，10，14。 (10)

式(10)中的通用模型可以利用优化算法进行求解，求得时域小波逼近函数()后进行拉普拉斯变换，获得滤波器的频域传递函数()。由于实小波函数的时域逼近问题转化成通用模型的优化求解，因此，该模型适合于任意实小波函数逼近。

2 任意阶开关电流实小波滤波器实现

2.1 双线性开关电流积分器和电流镜模型

开关电流技术是继开关电容技术后一种新的电流模式模拟取样数据信号处理技术，它可以采用数字CMOS工艺技术实现，代表混合模/数VLSI的未来发展方向。与电压模开关电容电路相比，开关电流电路具有电源电压低、频率宽、动态范围大、速度快和功耗小等优点。由于在实际设计中多端输出的开关电流积分器能够更加简化电路，所以，通常在开关电流积分器的输出端附加电流镜实现多端输出。本设计中采用的多输出开关电流双线性积分器电路和符号如图1所示，同相双线性积分器的域传递函数为

其中：o1为同相输出电流；−o1为反相输出电流；为积分器晶体管参数。

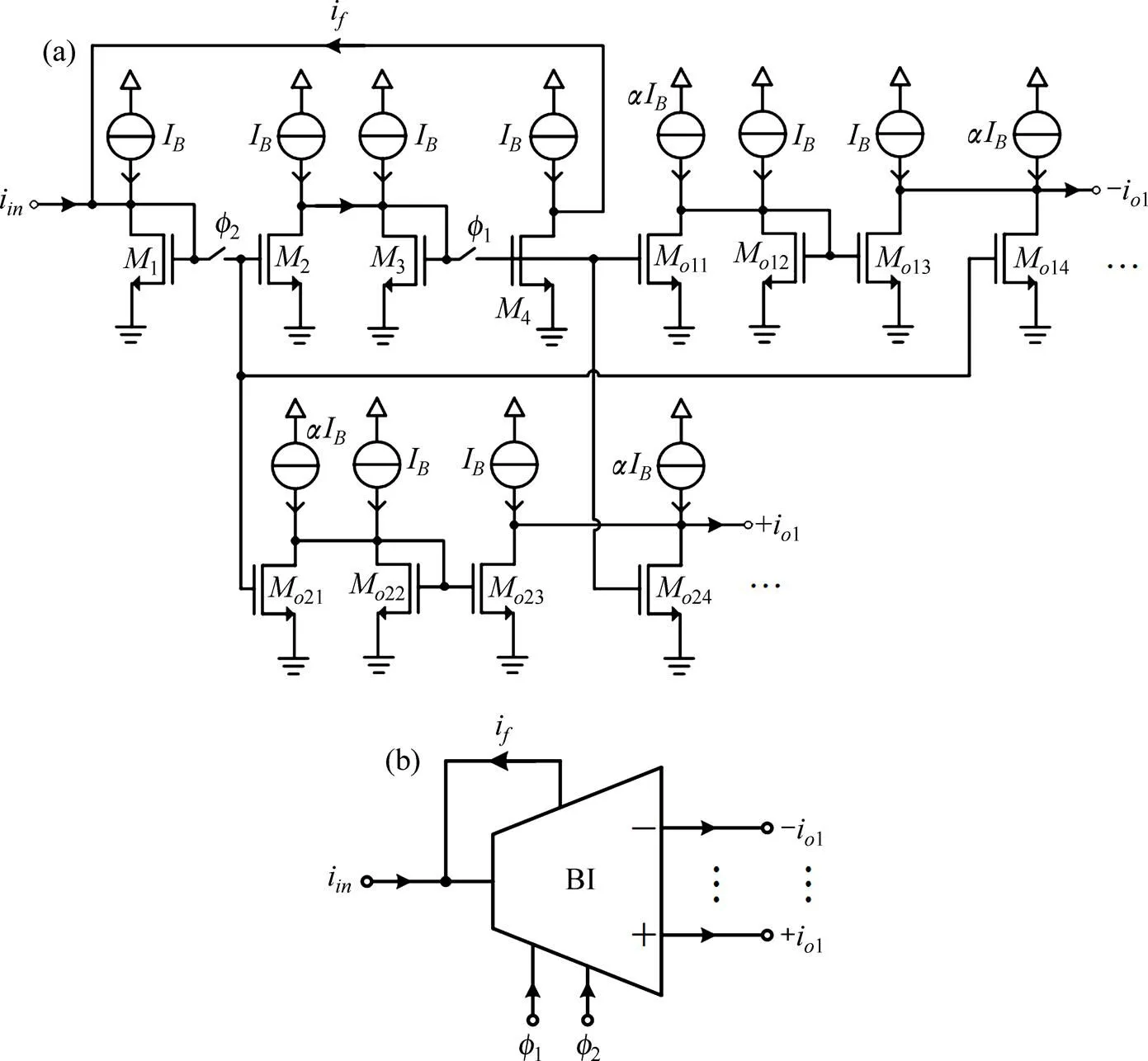
(a) 开关电流双线性积分器电路；(b) 电路符号

电流镜电路和符号如图2所示，其输入、输出关系式为

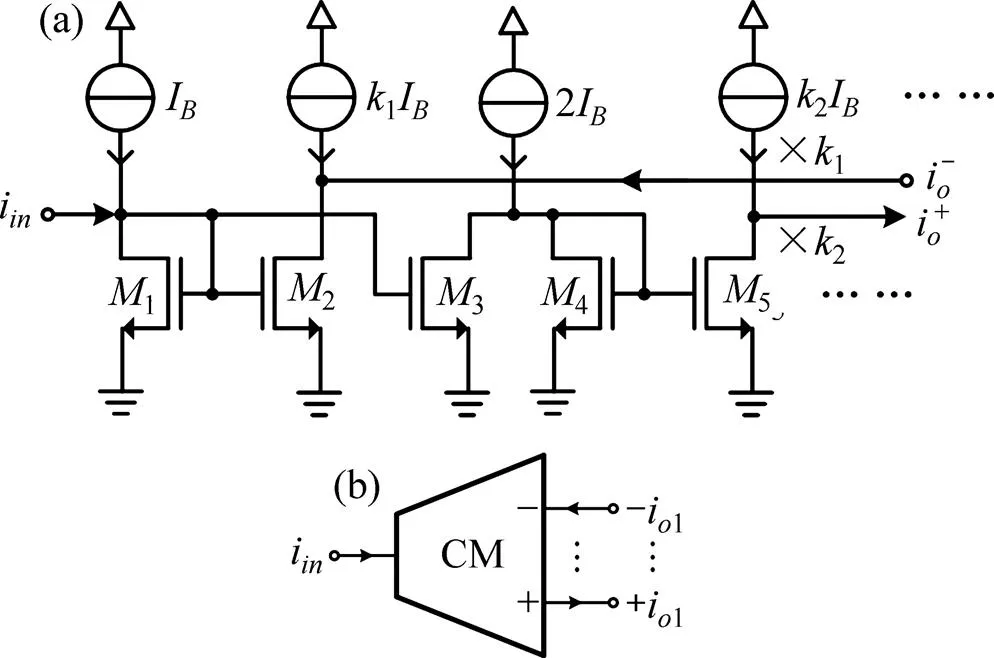
(a) 电流镜电路；(b) 电路符号

2.2 任意阶开关电流滤波器模型的实现

其中：A(=0，1，…，)和B(=0，1，…，)均为实系数。分析式(13)可知，它可以采用通用积分器()为基本单元设计滤波器实现，其中，为积分器的时间常数，则式(13)可以改写为

式(14)对应的FLF信号流图如图3所示。对比式(14)和式(13)可求得图3中的系数a和b分别为：

传递函数式(14)的FLF结构信号流图见图3，其中，信号流图对应的是连续系统。为了采用开关电流双线性积分器实现，需要将该连续系统进行离散化。只需将原连续系统中1/替换成(+1)/[2(−1)]，即可实现域系统的离散化。以开关电流双线性积分器为基本单元的通用FLF结构开关电流滤波器电路如图4所示。图4中，α，α和α分别为积分器参数、反馈网络系数和前馈网络参数，k1和k2为前馈网络系数。

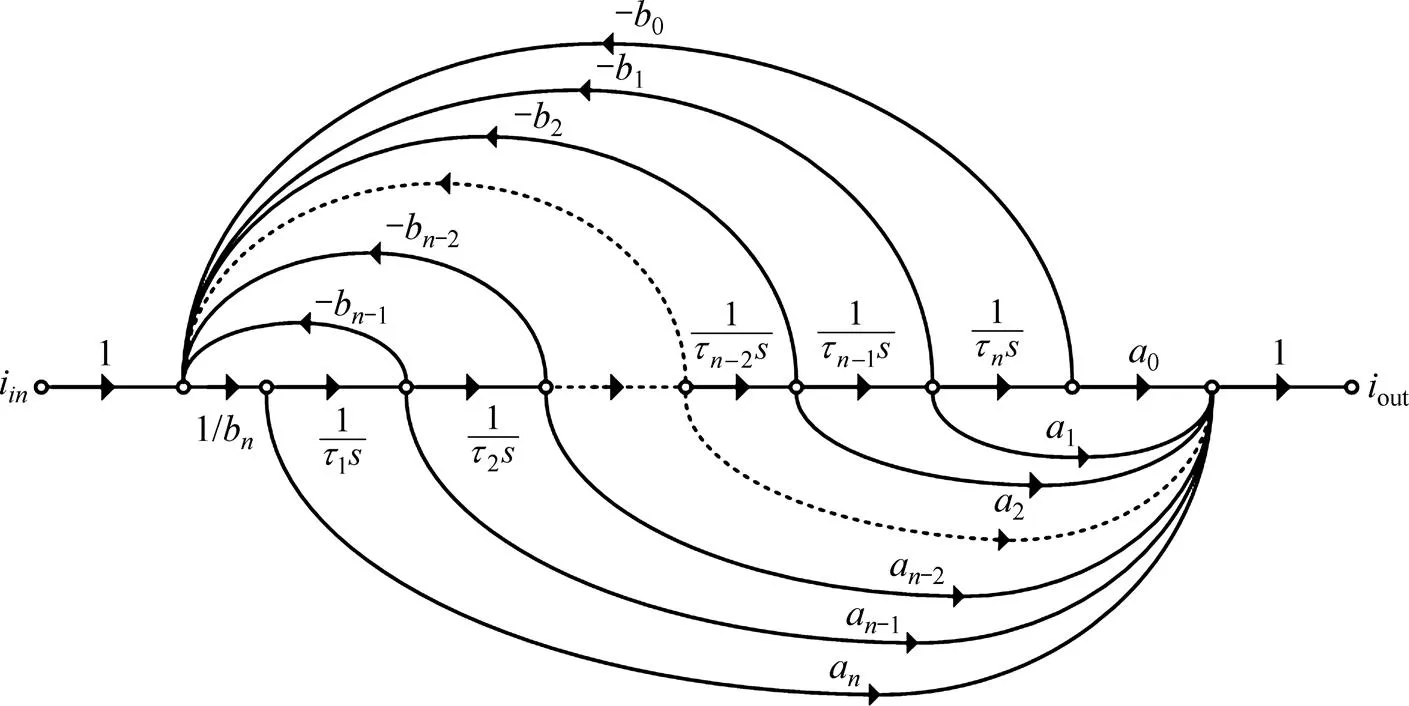
图3 传递函数式(14)的FLF结构信号流图

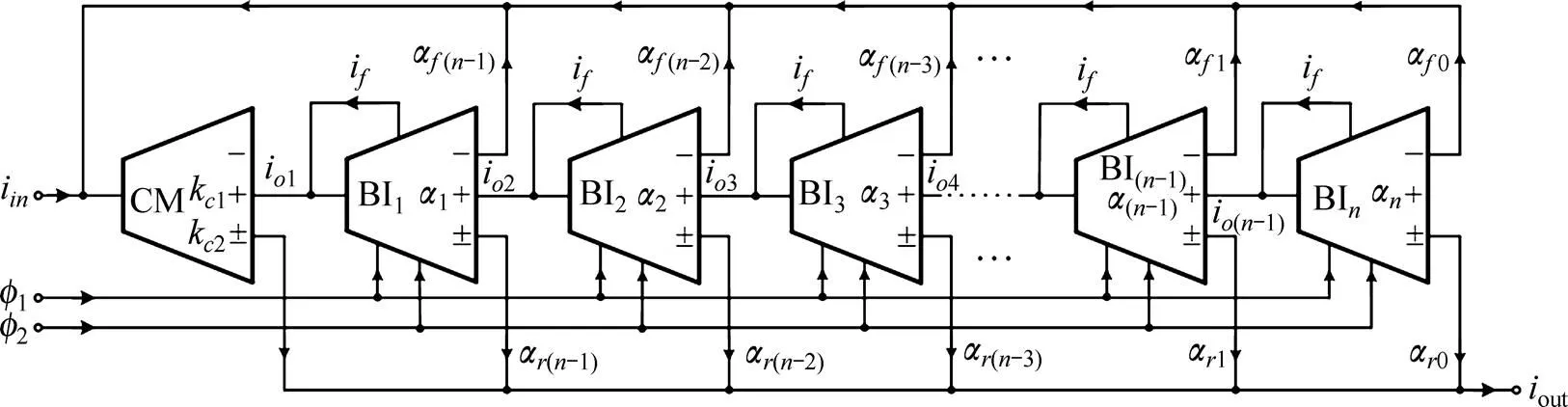
图4 通用FLF结构开关电流滤波器电路

(18)

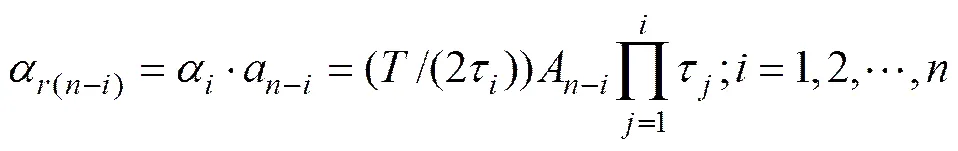
根据系统域传递函数，利用式(17)~(20)求开关电流双线性积分器的晶体管参数，即可实现任意实小波函数的高阶开关电流滤波器设计。

3 设计实例

采用该模型可以实现任意实小波函数的高阶开关电流滤波器。下面以实Morlet小波开关电流滤波器设计为例验证该模型的正确性。

3.1 实小波函数的量子差分进化算法逼近

量子差分进化算法(quantum differential evolution algorithm,QDE)[15−16]是将量子计算理论与差分进化算法相结合的优化算法。在该算法中，染色体由量子比特构成，并用实数对量子比特进行编码。通过采用量子旋转门和量子非门分别实现染色体的更新与变异，从而获得目标函数的最优解。

量子差分进化算法中的最小信息单元是量子比特，任意时刻量子比特的状态可表示为

其中：为当前迭代次数。式(22)用量子角形式可简化为。算法初始化种群时个体量子角在内随机生成。

为了评价进化过程中量子个体的优劣程度，需要对个体量子位状态进行测量，使其从量子角形式坍缩至经典比特形式。其实施方法为：对应量子个体中的每一位产生随机数，比较该随机数与，若，则个体中取值为“1”，否则为“0”。

QDE算法按照标准差分进化算法的变异、交叉和选择操作过程更新染色体量子比特状态。当前代的每个量子染色体按式(23)进行变异操作，得到相应的变异个体。

其中：r()为[1，]中的均匀分布概率；为种群中个体的维数；j为[1，]中的随机整数；为交叉概率。将和代入适应度函数，按式(25)进行选择操作，适应度最小的个体进入下一代。

其中：为适应度函数，即式(10)中的()表达式。

按上述量子差分进化算法的量子染色体编码、测量和量子染色体更新策略结合差分进化算法的基本步骤，对实Morlet小波函数进行8阶有理函数(如式(7))逼近。实Morlet小波函数的时域表达式为

设置种群规模p为10，Δ=0.01，采样点个数=800，最大进化代数=500，根据试凑法取变异率=0.7，交叉率C=0.85。采用量子差分进化算法求得8阶实Morlet小波逼近函数如图5所示，逼近均方误差为1.397 6×10−4，其频域表达式为

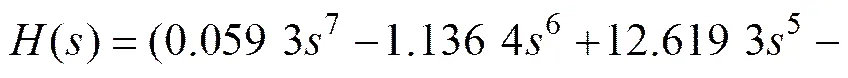
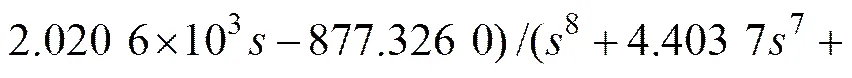
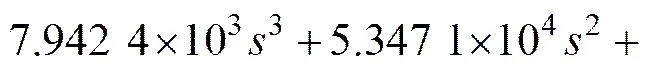
3.2 实Morlet小波滤波器实现与仿真分析

现将通过QDE算法逼近获得的式(29)去归一化后作为系统传递函数，采用图1中的开关电流双线积分器和图2中的电流镜电路为基本单元，以图4中的通用FLF结构开关电流小波滤波器电路为原型，设计实Morlet小波滤波器。将传递函数的中心频率去归一化至10 kHz，并取采样频率为100 kHz，令1=1，2=3=4=5=6=7=8=1/6，利用式(20)计算c1=1，c2=0，利用式(17)~(19)并结合式(29)计算其他晶体管跨导参数，如表1所示。

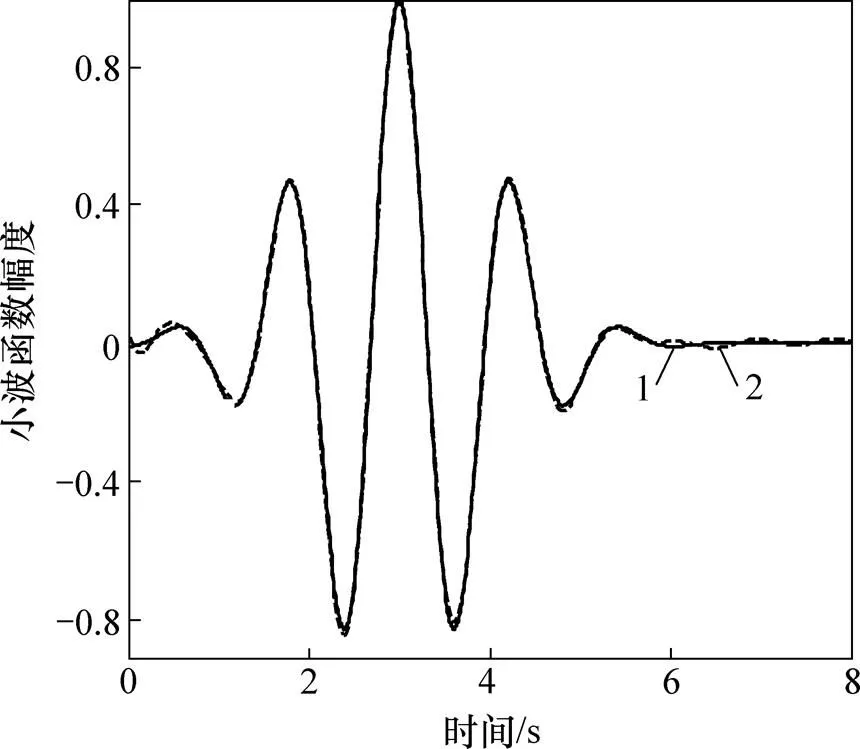
1—Morlet小波；2—小波逼近函数。

根据表1设置实Morlet小波滤波器中相应晶体管的参数，其余的晶体管跨导参数均设为1。由于开关电流电路的膨胀系数可通过调节电路时钟频率获得，因此，该电路只需改变时钟频率即可获得不同尺度小波函数。选取时钟频率分别为100.0，50.0，25.0和12.5 kHz，对应小波函数的尺度分别为1，2，4和8，采用ASIZ软件进行仿真，不同尺度下实Morlet小波滤波器的脉冲响应如图6所示。由图6可知：相应各尺度的时域波形分别在0.2，0.4，0.8和1.6 ms时获得最大正峰值0.173 3 A，与实Morlet小波函数归一化后的最大正峰值基本一致。

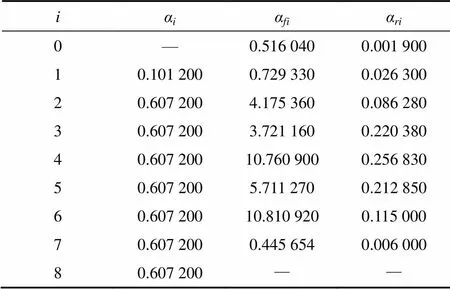
表1 实Morlet小波滤波器电路的晶体管跨导参数

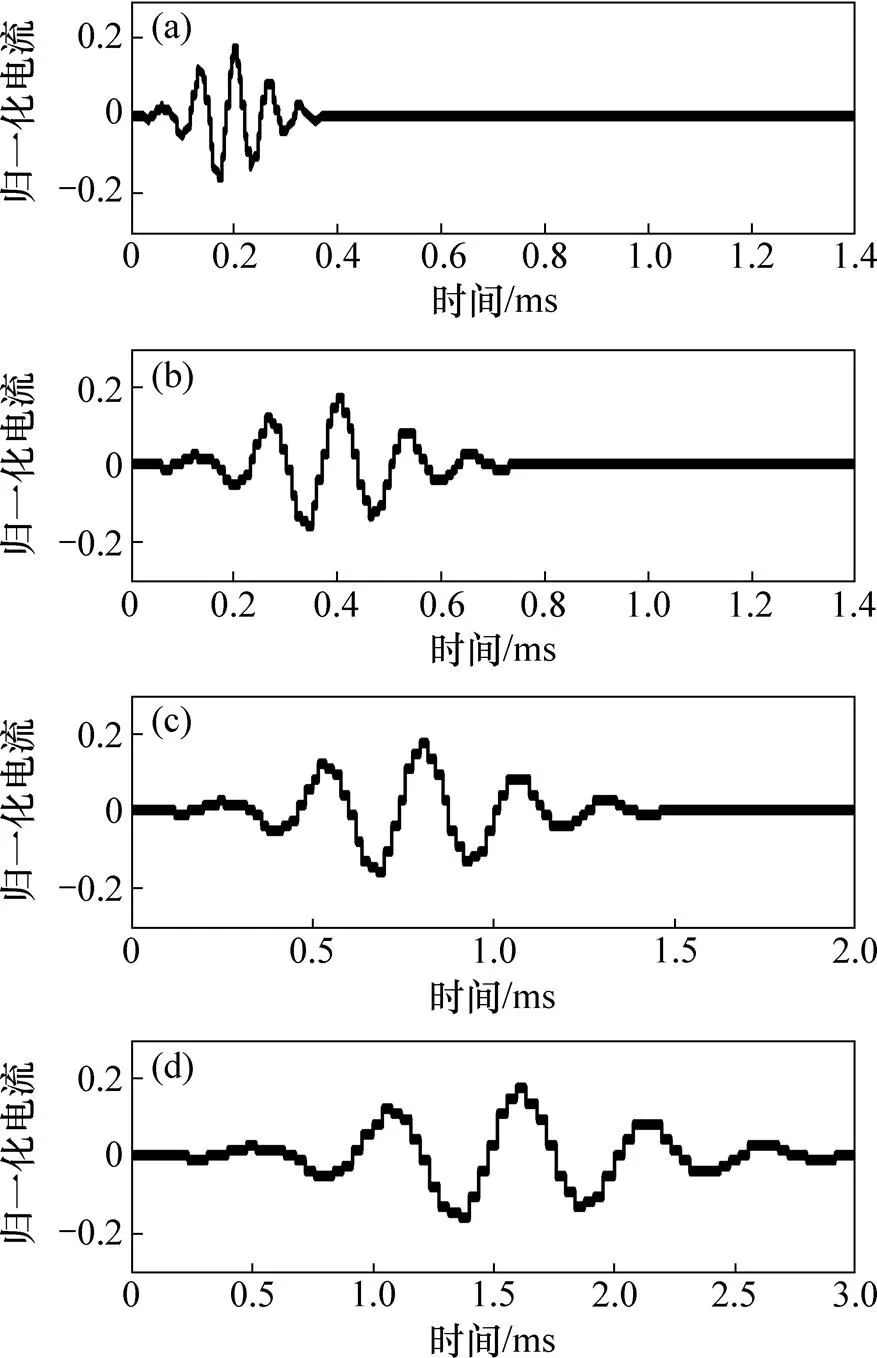
(a) a=1；(b) a=2；(c) a=4；(d) a=8

图7所示为尺度=1，2，4和8时实Morlet小波滤波器的频率冲响应和尺度=1时的零极点图。相应各尺度小波滤波器频率特性波形分别在10.432，5.216，2.608和1.304 kHz时取得峰值1.962 dB，与理想值1.975 dB很接近。此外，图7中的内插图给出了尺度=1时的零极点图，其中，“○”代表零点，“×”代表极点。由于所有极点都采用1/2的幂形式来表示，所以，对于8阶实Morlet小波滤波器，小窗口中有16个极点。由零极点图可见：所有极点均位于平面的单位圆内，因此，所构造的系统是稳定的。

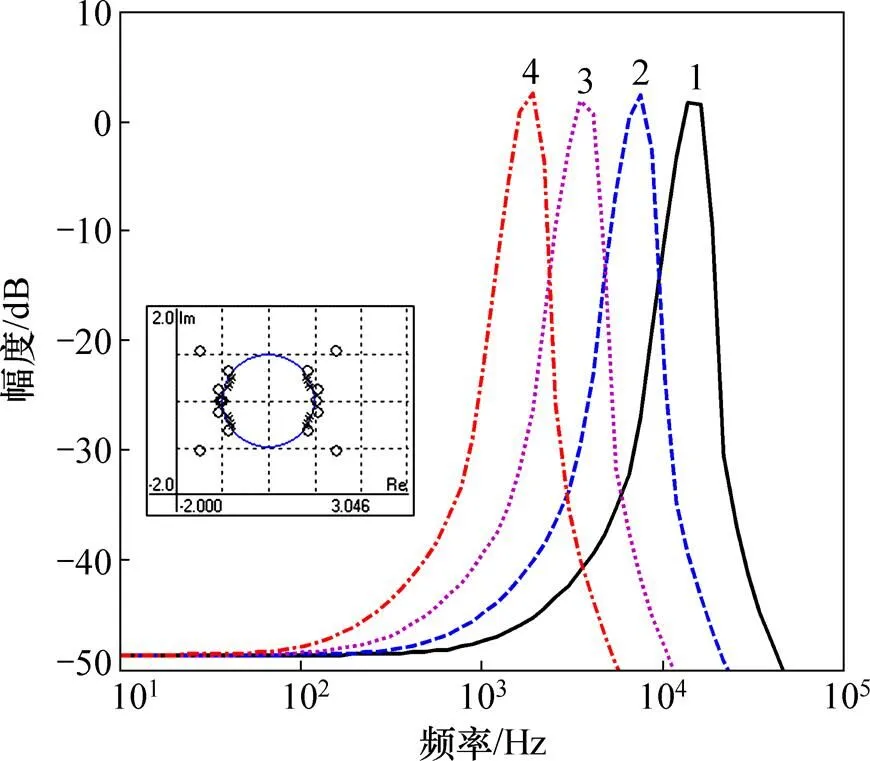
1—a=1；2—a=2；3—a=4；4—a=8。

上述开关电流实Morlet小波滤波器的时域、频域仿真结果证明了所提出的任意实小波函数的高阶开关电流滤波器通用实现方法的正确性。

4 结论

1) 针对现有实小波函数逼近方法的不足，提出了实小波函数的通用时域优化逼近模型，采用智能优化算法进行优化求解可获得高精度的时域小波逼近函数。该模型不但适合有解析表达式实小波函数逼近，而且适合无解析表达式实小波函数(如Daubechies小波)逼近。同时，该模型还可以推广到复小波函数的时域逼近。

2) 通过对任意电流模式传递函数进行数学分析，提出了一种可以实现高阶开关电流小波滤波器的综合设计模型，并以开关电流双线性积分器和电流镜实现具体的电路模型。该模型通用性和系统性强，可以应用于任意实小波函数的开关电流滤波器综合设计。

3) 以开关电流实Morlet小波滤波器实现为例，采用量子差分进化算法逼近实Morlet小波，并对滤波器电路进行了设计，仿真结果证明了该模型的正确性。所提出的模型可以在小波变换的模拟集成电路实现中得到广泛应用。

参考文献：

[1] MOREIRA-TAMAYO O, PINEDA DE GYVEZ J. Analog computation of wavelet transform coefficients in real-time[J]. IEEE Transactions on Circuits and Systems, 1997, 44(1): 67−70.

[2] MELÉNDEZ-RODRÍGUEZ M, SILVA-MARTINEZ J, SPENCER R. Efficient circuit implementation of Morlet wavelets[J]. Journal of Applied Research and Technology, 2005, 1(1): 60−72.

[3] 胡沁春, 何怡刚, 郭迪新, 等. 基于开关电流技术的时域连续小波变换实现[J]. 电子与信息学报, 2007, 29(1)227−231.HU Qinchun, HE Yigang, GUO Dixin, et al. Time-domain implementation of continuous wavelet transform based on switched current[J]. Journal of Electronics and Information Technology, 2007, 29(1)227−231.

[4] AKANSU A N, SERDIJN W A, SELESNICK W. Emerging application of wavelets:a review[J]. Physical Communication, 2010, 3(1): 1−18.

[5] KAREL J M H, HADDAD S A P, HISENI S, et al. Implementing wavelets in continuous-time analog circuits with dynamic range optimization[J]. IEEE Transactions on Circuits and Systems, 2012, 59(2): 229−242.

[6] GURROLA-NAVARRO M A, CARRASCO-ALVAREZ R, MEDINA-VAZQUEZ A S, et al. On-chip wavelet denoising system implemented with analogue circuits[J]. Electronics Letters, 2013, 49(9): 592−594.

[7] CASSON A J, RODRIGUEZ-VILLEGAS E. Nanowatt multi-scale continuous wavelet transform chip[J]. Electronics Letters, 2014, 50(3): 153−154.

[8] HADDAD S A P, BAGGA B, SERDIJN W A. Log-domain wavelet bases[J]. IEEE Transactions on Circuits and Systems, 2005, 52(10): 2023−2032.

[9] EDWARDS R T, GODFREY M D. An analog wavelet transform chip[C]//IEEE International Conference on Neural Networks.New York: IEEE, 19931247−1251.

[10] EDWARDS R T, CAUWENBERGHS G. A VLSI implementation of the continuous wavelet transform[C]//IEEE International Symposium on Circuits and Systems. New York: IEEE, 1996368−371.

[11] LIN J, KI W H, EDWARDS T, et al. Analog VLSI implementations of auditory wavelet transforms using switched-capacitor circuits[J]. IEEE Transactions on Circuits and Systems, 1994, 41(9): 572−583.

[12] 胡沁春, 何怡刚, 郭迪新, 等. 基于开关电流技术的小波变换的滤波器电路实现[J]. 物理学报, 2006, 55(2): 641−647.HU Qinchun, HE Yigang, GUO Dixin, et al. Analog implementation of wavelet transform based on using switched-current filter circuits[J]. Acta Physica Sinica, 2006, 55(2): 641−647.

[13] 赵文山, 何怡刚. 一种改进的开关电流滤波器实现小波变换的方法[J]. 物理学报, 2009, 58(2): 843−851. ZHAO Wenshan, HE Yigang. An improved method for implementation of wavelet transform utilizing switched-current filters[J]. Acta Physica Sinica, 2009, 58(2): 843−851.

[14] 李目, 何怡刚. 基于开关电流双线性积分器的IFLF小波滤波器设计[J]. 电路与系统学报, 2013, 18(2): 191−195. LI Mu, HE Yigang. IFLF wavelet filters design based on switched-current bilinear integrators[J]. Journal of Circuits and Systems, 2013, 18(2): 191−195.

[15] 陈晓峰, 杨广明, 黄明. 一种实数编码的量子差分进化算法[J]. 小型微型计算机系统, 2013, 34(5): 1141−1146. CHEN Xiaofeng, YANG Guangming, HUANG Ming. Real-coded quantum differential evolution algorithm[J]. Journal of Chinese Computer Systems, 2013, 34(5): 1141−1146.

[16] 任子武, 熊蓉, 褚健. 混合量子差分进化算法及应用[J]. 控制理论与应用, 2011, 28(10): 1349−1355. REN Ziwu, XIONG Rong, CHU Jian. Hybrid quantum differential evolutionary algorithm and its applications[J]. Control Theory and Applications, 2011, 28(10): 1349−1355.

(编辑 陈灿华)

General implementation of arbitrary real wavelet function with high order switched-current filters

LI Mu1, WU Xiaofeng1, XI Zaifang1, HU Shigang1, LI Jin1, WU Shuyue2

(1. College of Information and Electrical Engineering,Hunan University of Science and Technology, Xiangtan 411201, China;2. School of Information and Science Engineering,Hunan International Economics University, Changsha 410205, China)

A new general synthesis method for high order switched-current filter implementation of arbitrary wavelet function was presented. The method was based on the analytical decomposition of the filter implementation with real wavelet function approximation and wavelet filter design by the analog filter implementation principle of wavelet function. The filter circuit was designed as follows. Firstly, a general optimization approximation model of real wavelet function was structured based on synthesis theory of network systems. Then the general multiple-loop feedback structure filter whose impulse response was the approximated real wavelet function was designed using switched-current bilinear integrators and current mirrors as the basic building blocks. By changing the clock frequency of the filter circuit, the different scale wavelet functions were very precisely obtained. Finally, a switched-current real Morlet wavelet filter was employed to demonstrate the correctness of the realization scheme.

switched-current circuits; wavelet function; function approximation; wavelet filter design

10.11817/j.issn.1672-7207.2016.10.019

TN713

A

1672−7207(2016)10−3417−07

2015−12−10；

2016−02−09

国家自然科学基金资助项目(61404049，61474042，U1501253)；湖南省科技计划项目(2013FJ2011, 2014FJ2017)；湖南省教育厅项目(14A084，14B060)；湖南科技大学科研项目(E51525)；湘潭市科技计划项目(CG20121006) (Projects(61404049, 61474042, U1501253) supported by the National Natural Science Foundation of China; Projects(2013FJ2011, 2014FJ2017) supported by the Science and Technology Plan Foundation of Hunan Province; Projects(14A084,14B060) supported by the Scientific Research Fund of Education Department of Hunan Province; Project(E51525) supported by the Scientific Research Fund of Hunan University of Science and Technology; Project (CG20121006) supported by the Science and Technology Plan Foundation of Xiangtan City)

李目，博士，副教授，从事高速低压低耗集成电路与系统、模拟信号处理、模拟电路测试与诊断和智能信息处理等研究；E-mail：limuucn@163.com