成败型产品可靠性的Bayes验收方案研究

刘海涛，张志华2，董理3

（1.海军工程大学理学院，湖北武汉430033；2.海军工程大学科研部，湖北武汉430033；3.海军工程大学兵器工程系，湖北武汉430033）

成败型产品可靠性的Bayes验收方案研究

刘海涛1，张志华2，董理3

（1.海军工程大学理学院，湖北武汉430033；2.海军工程大学科研部，湖北武汉430033；3.海军工程大学兵器工程系，湖北武汉430033）

针对成败型产品生产定型阶段的可靠性验收问题，为了合理综合利用产品定型阶段以前的先验信息，利用竞争失效方法建立了产品定型阶段和批生产阶段的可靠性信息转换模型，进而确定了批产品生产可靠度的先验分布。在此基础上，给出了其后验分布、风险的计算方法以及Bayes验收方案的制定方法。实例分析表明，该方法能够大大减少验收试验量，且方法稳健。

数理统计学；可靠性；验收试验；Bayes方法；成败型产品；批生产

0 引言

产品可靠性验收试验是产品验收阶段的一项重要工作。在产品已通过定型并批准转入批生产的情况下，可靠性验收试验的目的是通过在规定条件下进行试验，确定批产品可靠性是否符合规定要求［1］。目前，产品可靠性验收试验方案主要可从国家和军用标准中选取。但是，现有标准提供的试验方案一般要求较大的试验量，特别是对于许多技术复杂、造价昂贵、研制经费紧张的大型复杂产品，验收试验产生的费用往往难以承受，导致实施存在困难。

事实上，在大型产品的研制过程中，通常会进行环境应力筛选试验和可靠性鉴定试验等，因此，将产品定型阶段的可靠性鉴定试验信息作为批产品验收的先验信息可以大大减小试验量。如文献［2-3］利用可靠性鉴定试验信息确定批产品失效率的先验分布，分析了不同保证试验方案的风险问题。文献［4］针对装备研制过程中存在多阶段试验信息的特点，提出一种变总体下的Bayes可靠性试验鉴定方法。文献［5］针对传统Bayes方法对验前信息和现场信息不加区分的缺点，提出一种融合多源验前信息的成败型产品可靠性评估模型。但是，上述方法对如何将不同研制阶段的产品信息转化为批产品的先验信息讨论较少。

实际上，可靠性鉴定试验的主要目的是验证产品的设计水平和零部件选用是否达到任务规定的要求。而在批生产过程中，生产工艺（材料的选用、生产设施、人员的操作技术与管理水平）等方面可能存在一定问题，因此在批生产阶段特别是生产初期，批产品可靠度将低于定型可靠度。也就是说，批产品的可靠性是由其设计、零部件及生产工艺等因素决定的，而可靠性鉴定试验主要是发现产品的设计和零部件缺陷，对生产工艺中存在的缺陷则无法充分考察［6-7］，因此，直接利用可靠性鉴定试验信息确定批产品可靠度的先验分布并不合理。针对这一问题，文献［8］利用竞争失效模型建立产品定型阶段和批生产阶段的可靠性信息转换模型，进而确定批产品失效率的先验分布并对验收试验风险进行定量分析，但是该方法只针对指数分布进行了分析。

因此，本文以成败型产品为研究对象，通过建立竞争失效模型对产品定型阶段的试验信息进行综合，给出批产品可靠度的先验分布。在此基础上，对验收试验的风险进行分析，并给出验收试验方案的制定方法。

1 基于竞争失效模型的先验分布确定

1.1竞争失效模型

由上文分析可知，批产品的失效机理可分为设计缺陷、零部件缺陷和工艺缺陷3种，其中任何一种机理的发生均会导致失效。因此，批产品失效实际是由设计缺陷、零部件缺陷和工艺缺陷共同组成的竞争失效模型。

而在产品研制阶段，工程人员主要关注产品设计的合理性以及零部件缺陷，因此，研制阶段的产品失效主要由设计缺陷和零部件缺陷引起。记pd、pc（0＜pd，pc＜1）分别为设计缺陷和零部件缺陷所引起产品失效的概率，则Rd=1-pd，Rc=1-pc分别为设计缺陷和零部件缺陷不引起产品失效的概率，称其为设计可靠度和零部件可靠度。由竞争失效模型可知［9］，产品定型可靠度为

通过定型试验的产品转入批生产阶段后，设pp为工艺缺陷所引起批产品失效的概率，则批产品的生产可靠度R［9］为

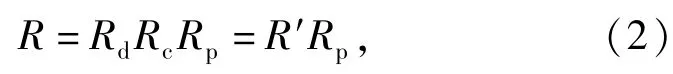
式中：Rp=1-pp为工艺缺陷不引起产品失效的概率，称其为工艺可靠度，pp为工艺缺陷引起的产品失效概率。

由（2）式可知，批产品的生产可靠度R与定型可靠度R＇及工艺可靠度Rp有关。为了对批产品的生产可靠度R进行评估，可以首先对产品定型可靠度R＇和工艺可靠度Rp进行评估，然后利用（2）式得到批产品的生产可靠度R的评估结果。但是，工艺可靠度的评估往往比较困难，特别是在产品初期，可用于评估的信息非常少。

为此，对（2）式两边取对数，得到：

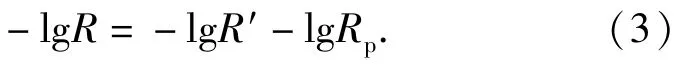
由此，可以定义比例系数ω为

对于（4）式，在产品可靠度较高的条件下，利用1阶泰勒展开可以得到：

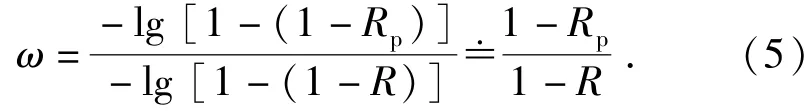
由于在试验量为N时，N（1-Rp）实际上表示了由工艺缺陷所引起的失效个数，N（1-R）则表示了产品的总失效个数，因此，系数ω可近似表示因工艺缺陷引起产品失效占产品失效总数的比例，它综合反映了批产品的生产工艺水平，可利用批产品的实际使用数据或专家经验信息等确定。

由（3）式和（5）式可以得到：

1.2生产可靠度的先验分布

由（6）式可知，为了得到生产可靠度R的先验分布，需要确定定型可靠度R＇的先验分布与系数ω.由于ω表示批产品因工艺缺陷造成产品失效占总失效数的比例，因此当批产品使用信息较多，可以较为准确地估计ω并将其作为常数处理；当批产品使用信息不多，即关于系数ω的信息较少时，可以将系数ω视为随机变量，并利用掌握的先验信息确定它的先验分布。本文以将ω视为常数为例进行分析。

为了得到定型可靠度R＇的先验分布，首先设分布形式为共轭先验分布Beta（R＇|a0，b0），其密度函数为

式中：a0、b0为超参数。

由于可靠性鉴定试验可能采用一次抽样检验、二次抽样检验、多次抽样检验以及序贯抽样检验等不同方案，所得到的数据形式也不相同，因此，为叙述的统一起见，不妨从可靠性鉴定试验的定型结论出发构造其先验分布。

记可靠性鉴定试验的定型结论为：1）在置信水平γ下，可靠度置信下限为R＇L；2）可靠度的点估计为则超参数a0、b0可利用下列方程组［10］求得

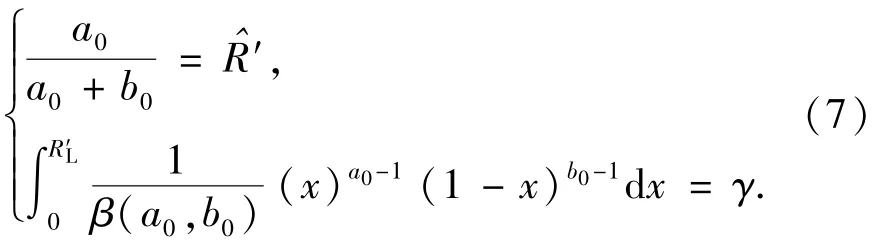
由此，利用（6）式和（7）式，在给定系数ω的情况下，可以得到批产品生产可靠度R的先验分布为

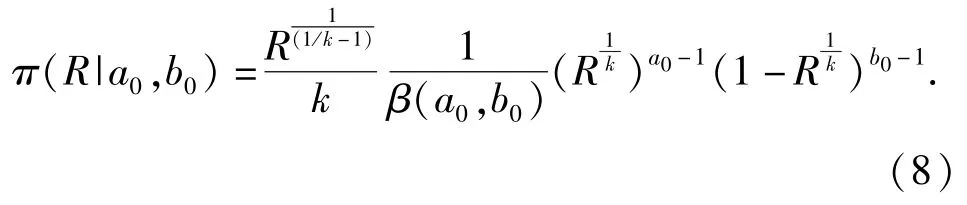
但是，（8）式所示的先验分布在实际使用中并不方便。为了工程应用方便，使用 Beta分布Beta（R|a，b）作为先验分布式（8）式的近似分布，即批产品生产可靠度R的先验近似分布为Beta（R|a，b），此时参数a、b［7］满足

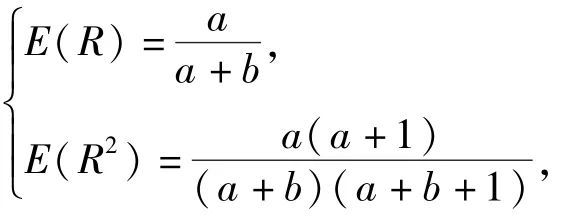
即

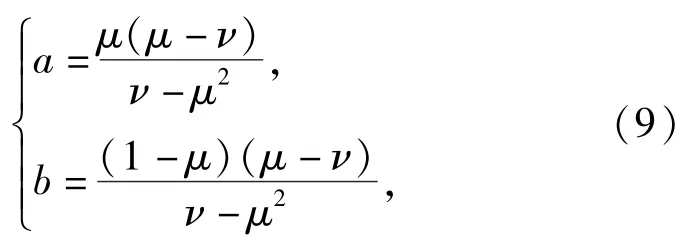
式中：μ、ν分别表示批产品生产可靠度R的1阶矩和2阶矩，即

2 验收方案的制定

2.1后验分布的确定

对给定的批产品生产可靠度R的先验分布Beta（R|a，b）和任一生产定型试验结果（N，r），其后验密度函数为

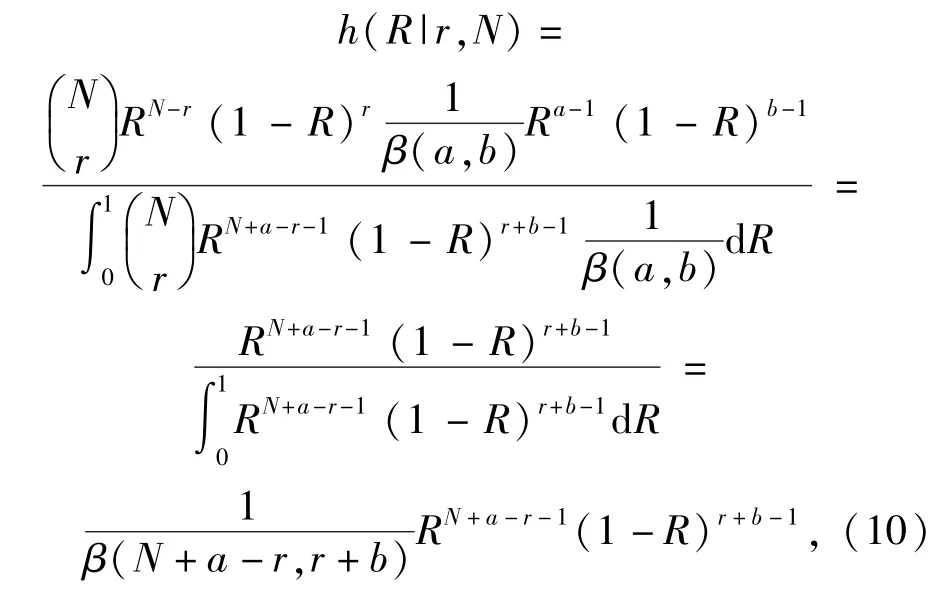
后验概率为

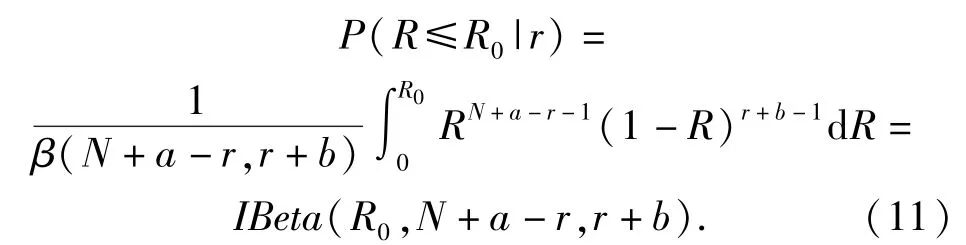
2.2风险分析

记合格质量水平为R0，对于生产方，其风险为合格产品没有通过验证试验而被拒收的概率，即P（没通过检验|R≥R0），也即

若给定生产方风险α，则只需要求

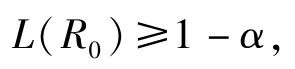
特别地

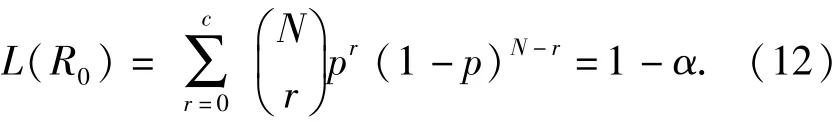
记极限质量水平为Rl，使用方风险为β，对于使用方而言，其风险为接收的产品为不合格产品的概率，即P（R≤Rl|通过检验），即

特别地

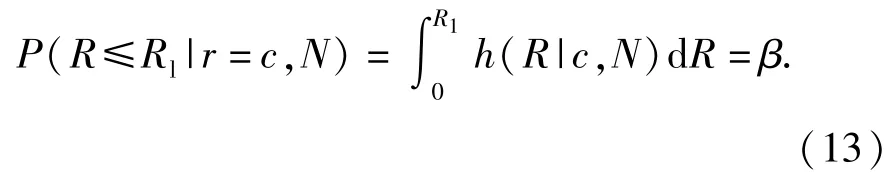
2.3方案的制定

综上，只需要求制定的验证试验方案（N，c）满足（12）式和（13）式的联立方程组

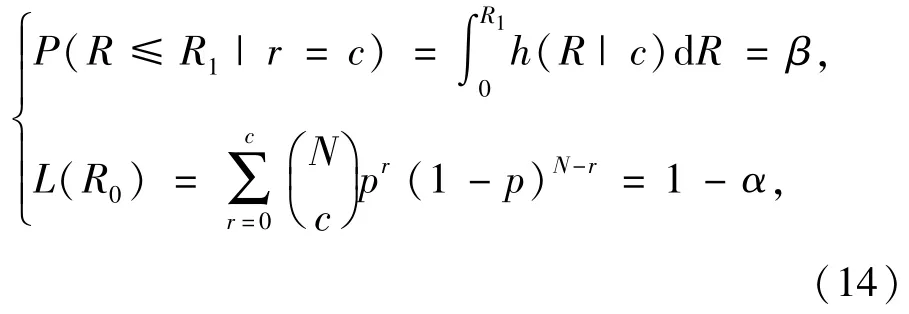
即可满足生产与使用双方对风险的要求，保证双方的利益。其方案制定步骤为：

1）对给定的使用方风险β和产品可靠度的目标值Rl，利用（13）式求出总试验次数N；

2）计算L（R0），如果（12）式不满足（即达不到生产方可接受的要求），则在使用方允许的范围内适当调整使用方风险β或合格质量水平R0。重复上述步骤。

3 实例分析

设某成败型产品的合同书规定其任务可靠度为R0=0.999.综合考虑生产方和使用方因素，确定其可靠性验收试验的相关参数为：合格质量水平R0= 0.999，鉴别比d=2.0；生产方风险α=30%；使用方风险取β=30%.同时，已知该产品在定型阶段的可靠性鉴定试验中共进行了648次试验，均未发生失败。

3.1经典验收试验方案

查阅国家标准GB5080.5—85，可以容易地获得批产品的经典一次计数抽样验收试验方案，如表1所示。

表1　某成败型批产品可靠性验收试验的经典方案Tab.1 Classical reliability testing schemes for a batch of binominal products

3.2Bayes验收试验方案

由已知可靠性鉴定试验数据（648，0），根据（9）式可以得到系数ω下生产可靠度R的先验分布Beta（R|a，b），如表2所示，例如当ω=1/10时，代入（9）式可求得a=583.199 9，b=1.000 0.在已知批产品可靠度的先验分布Beta（R|a，b）的情况下，由（10）式和（11）式可以得到批产品可靠度后验密度函数和后验概率。

然后按照2.3节验收方案的制定步骤，可以得到相应的Bayes验收试验方案，如表2所示。其中，N0为失效数为0时的验收方案，N1为失效数为1时的验收方案，N2为失效数为2时的验收方案，N3为失效数为3时的验收方案。

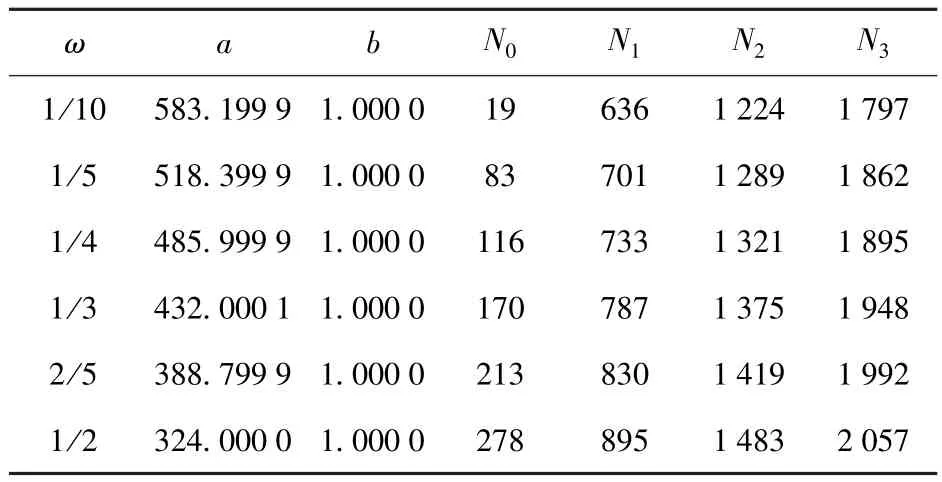
表2　某成败型批产品可靠性Bayes验收方案及相关参数Tab.2 Bayesian reliability testing schemes and parameters for a batch of binominal products

由表2可以看到，随着ω的增大，也即工艺缺陷对产品的影响越来越大，验收试验量平稳地增大。例如，ω=1/4时的无失效方案为116，ω=1/3时的无失效方案为170，ω=2/5时的无失效方案为213，可见随着工艺缺陷影响的增大，试验量增加的幅度较为平稳，如从ω=1/4增加到ω=1/3时试验量增加54，而从ω=1/3增加到ω=2/5时试验量则增加43.

4 结论

对许多价值昂贵的大型复杂产品，传统可靠性验收方法所要求的试验量过大，导致验收方案难以实施。针对此问题，分析了成败型产品可靠性的Bayes验收方案制定问题，利用竞争失效模型对定型阶段和批生产阶段的可靠性信息进行合理综合，在此基础上，给出了其Bayes验收方案的制定方法。实例分析表明，该方法具有较好的稳健性，且通过合理利用可靠性先验信息，大大减少了验收试验量。下一步，可利用该思路进一步研究产品验收可靠度的评估问题。

（References）

［1］ 张志华，田艳梅，郭尚峰.指数型产品可靠性验收试验方案研究［J］.系统工程与电子技术，2005，27（4）：753-756. ZHANG Zhi-hua，TIAN Yan-mei，GUO Shang-feng.Bayesian scheme of acceptance test in exponential case［J］.Systems Engineering and Electronics，2005，27（4）：753-756.（in Chinese）

［2］ 陈家鼎，张绡.关于MIL-HDBK-781中的保证试验［J］.数理统计与管理，2000，19（2）：39-45. CHEN Jia-ding，ZHANG Xiao.On theassurance tests in MIL-HDBK-781［J］.Application of Statistics and Management，2000，19（2）：39-45.（in Chinese）

［3］ 洪国钧，安伟光，刘玉明.平均故障时间保证试验风险研究［J］.中国造船，2000，41（1）：73-81. HONG Guo-jun，AN Wei-guang，LIU yu-ming.Study on MTBF assurance test risks［J］.Shipbuilding of China，2000，41（1）：73-81.（in Chinese）

［4］ 邢云燕，武小悦.成败型系统变总体下的Bayes可靠性试验鉴定方法［J］.系统工程理论与实践，2011，31（2）：323-327. XING Yun-yan，WU Xiao-yue.Bayesian reliability test evaluation for binomial system in varying population case［J］.Systems Engineering-Theory&Practice，2011，31（2）：323-327.（in Chinese）

［5］ 刘晗，郭波.融合多源验前信息的成败型产品可靠性Bayes评估［J］.弹箭与制导学报，2007，27（2）：338-341. LIU Han，GUO Bo.Fusion ofinformation of multiple sources in Bayesian assessment for reliability of success or failure product ［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2007，27（2）：338-341.（in Chinese）

［6］ 张详坡，尚建忠，陈循，等.三参数Weibull分布竞争失效场合加速寿命试验统计分析［J］.兵工学报，2013，34（12）：1603-1610. ZHANG Xiang-po，SHANG Jian-zhong，CHEN Xun，et al.Statistical inference of accelerated life test with competing failures based on three-parameter Weibull distribution［J］.Acta Armamentarii， 2013，34（12）：1603-1610.（in Chinese）

［7］ 张志华.可靠性理论及工程应用［M］.北京：科学出版社，2012. ZHANG Zhi-hua.Reliability theory and engineering applications ［M］.Beijing：Science Press，2012.（in Chinese）

［8］ 张志华.可靠性保证试验的风险分析［J］.兵工学报，2006，27（6）：1060-1063. ZHANG Zhi-hua.Riskanalysis of reliability assurance test in the case of exponential distribution［J］.Acta Armamentarii，2006，27（6）：1060-1063.（in Chinese）

［9］ 张英芝，牛序磊，申桂香，等.基于竞争失效模式的数控机床可靠性建模［J］.系统工程理论与实践，2014，34（8）：2144-2148. ZHANG Ying-zhi，NIU Xu-lei，SHEN Gui-xiang，et al.Numerically-controlled machine reliability modeling based on competing failure mode［J］.Systems Engineering-Theory&Practice，2014，34（8）：2144-2148.（in Chinese）

［10］ 徐志军，张博，王凯，等.基于Beta分布的改进的一次可靠度法研究［J］.土木工程与管理学报，2014，31（3）：17-21. XU Zhi-jun，ZHANG Bo，WANG Kai，et al.Study of modified first order reliability method based on Beta distribution［J］.Journal of Civil Engineering and Management，2014，31（3）：17-21.（in Chinese）

Bayesian Acceptance Test Scheme for Reliability of Binomial Products

LIU Hai-tao1，ZHANG Zhi-hua2，DONG Li3
（1.College of Science，Naval University of Engineering，Wuhan 430033，Hubei，China；2.Office of Research&Development，Naval University of Engineering，Wuhan 430033，Hubei，China；3.Department of Weaponry Engineering，Naval University of Engineering，Wuhan 430033，Hubei，China）

For the acceptance test of binominal products in the production definition phase，an information transition model for type approval phase and batch production phase is established using competitionfailure method in order to properly use the prior information of the type approval phase.The prior distribution of batch products’reliability is presented.On this basis，the calculation method of posterior distribution and risk is given，and a Bayesian acceptance test scheme is proposed.The experimental results show that the proposed method can be used to enormously reduce the acceptance test，and has preferable stability.

mathematical statistics；reliability；acceptance test；Bayesian method；binominal product； batch production

O213.2

A

1000-1093（2016）03-0565-05

10.3969/j.issn.1000-1093.2016.03.025

2015-03-01

海军工程大学自然科学基金项目（HGDQNEQJJ15002）；海军工程大学社会科学基金项目（HGDSKJJ2015E10）

刘海涛（1982—），男，讲师，博士。E-mail：liuhaitao0211@163.com