图像恢复的正则化混合WGMRES算法
丁伯伦,陈光喜
(1.安徽工程大学机电学院,安徽 芜湖 241000;2.桂林电子科技大学,广西 桂林541004)
图像恢复的正则化混合WGMRES算法
丁伯伦1,陈光喜2
(1.安徽工程大学机电学院,安徽 芜湖 241000;2.桂林电子科技大学,广西 桂林541004)
基于GMRES算法在处理大规模线性系统的优势,提出了一种图像恢复的正则化混合WGMRES算法。该方法是将加权的GMRES算法与正则化技术结合起来应用于图像恢复问题,首先建立一个特定的图像退化模型方程,在此基础上结合Tikhonov正则化技术将方程转化为一适定问题,然后利用改进的加权GMRES算法进行求解。数值试验结果表明改进算法复原后的图像较于标准GMRES算法复原后的图像在整体视觉效果上和峰值信噪比上都有很大提高。
GMRES算法;线性系统;正则化;模型方程;图像恢复
图像恢复的研究初始于二十世纪中叶,是图像处理早期的研究方向之一,在视觉处理运用中发挥着重要作用。目前该技术已经趋于成熟,并广泛应用于射电天文学、工业视觉、医学成像等领域。而作为数字图像处理的基本问题之一,图像恢复的主要目的是将退化图像复原为原始的图像。在一般情况下图像退化模型可以用下面的线性模型方程[1]来描述:
g=Hf+n(1)
其中,g、f、n分别为退化的模糊图像、原始图像和噪声按行堆叠而成的列向量,H为模糊算子矩阵,它具有分块循环的形式。图像恢复有两大特点:一是规模很大,方程中的模型算子一般为一个大型稀疏非对称线性方程组;二是由于图像恢复问题是一个典型的反问题,求解过程一般具有不适定性[2],所以噪声因素对最终解的准确性影响非常大。
GMRES算法是一种迭代算法,常用来求解大型稀疏且为非对称线性方程组的解。思想是通过Krylov子空间中得到的最小残量来趋近方程组的精确解,由于该算法的时间复杂度与空间复杂度都为O(N2)[3],所以在计算中具有计算量和内存量较少等优势,可以广泛应用在一些工程领域中,如:图像恢复、最优化控制、滤波理论等线性方程问题[4]。20世纪中下叶,介于GMRES算法处理大规模线性系统的优势,将算法与正则化技术结合来恢复因移动或者噪声产生的退化图像问题;在2012年,针对一个Otto Strnad问题,探究发现理想中的近似GMRES算法也可以用来解决相关界的问题[5];于 2013年,结合滤波理论提出GMRES迭代算法关于超声层析成像(UPT)[6]在多相流测量中的应用。GMRES算法所涉及的研究领域比较广泛,本文研究的是将算法应用在图像恢复问题上。
文章中所涉及的WGMRES算法是在标准GMRES方法上改进后的算法,也可将其看成是对标准GMRES方法进行的一个简单的预处理。然后在建立的图像退化模型的基础上将其与正则化技术结合并应用于图像恢复问题中。实验结果表明该方法对退化的图像有一定的恢复效果,并且相较于利用标准GMRES算法,图像的改善情况要更好些。
1WGMRES算法
GMRES算法是Saad和Schultz基于Galerkin原理[7]而提出的。基本思路是先通过Arnoldi过程求出Krylov子空间,即先求出Km(H,r0)=span{r0,Hr0,…Hm-1r0}的一组标准正交基,再将线性方程组投影到m维Krylov子空间Km(H,r0)上,最后经过迭代使残量极小化,求得方程组的解。WGMRES算法是在标准GMRES算法基础上加以改进的算法,求解的思路和标准GMRES算法是一样的,只是在Arnoldi过程中范数计算时引入了一个D内积的概念,所以涉及相关向量的范数表达形式将产生一些改变。这种改变得到的WGMRES算法较于GMRES算法有更好的收敛性也就是说得到的计算结果将更精确[8]。
1.1Arnoldi过程
需要先定义一个D内积,其中D=(d1,…,dn)为一个对角阵,且di>0(1≤i≤n),任取两个向量u,v∈Rn,则它们的D内积可写为
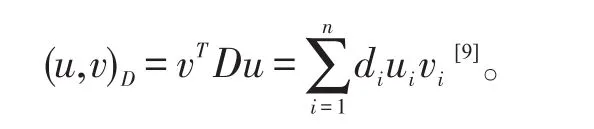
相应的范数可定义为:

对等式两边平方得:
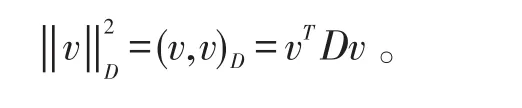
根据上述所定义的内积我们可以做出Arnoldi过程。具体算法步骤如下:
算法1
Step1:选取元素v1,使得=1;
Step2:对 j=1,...,k有vj+1=Avj,对i=1,...,j有
通过算法计算出一组关于D的正交基Vk=,可知其满足下列恒等式[10]
而且在计算过程中也得到了一个(k+1)×k的上Hessenberg矩阵,满足

1.2 微变型的WGMRES算法
随着算法的迭代次数不断增加,近似解也越来越接近原方程组的精确解。当形成第k步近似解时有:xk=x0+Vkyk,yk∈Rk,此时对应的残量表达式为rk=r0-AVkyk。基于此有这样的一个等式成立:,用D范数替换原先的2范数,根据算法1得到的关系式(2)和(3),可以得出下列等式:

经过一系列推导,(4)式可以变为下面的残量表达式[12]
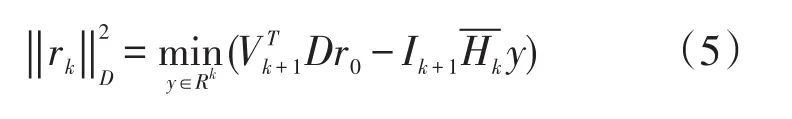
令-gk=VTk+1Dr0,则(5)式可变为:

这里改变了WGMRES算法关于残量表达式的形式,而且可以看出(6)式也是一个最小二乘问题,只要解出y,就能够得到所要求的第k步近似解xk。再由残量表达式rk=b-Axk计算出残量rk,最后根据残量rk的情况来决定迭代是否终止。
算法2
Step1:选取初始值 x0,计算初始残量r0=b-Ax0;
Step2:择取合适的d,比如di∈(0.5,1.5),并计算
Step3:通过算法1计算一组关于D的正交基Vk;
Step5:解出近似解xk=x0+Vkyk,进而得出残量表达式rk=b-Axk;
Step6:依据rk的结果来判断迭代是否终止;
Step7:若迭代终止则得到精确解xk;若结果不满足,需令x0=xk,r0=rk按照本算法中的第二步重新开始迭代,直到得出满意结果为止。
2 图像恢复的正则化混合WGMRES方法
对于图像恢复问题,有个图像降质过程,方程表达形式为(1)式,而对于空不变的时候,它是一个分块Toeplitz矩阵[13]。由于图像恢复问题是一个不适定反问题,所以可以使用正则化方法来确定近似解。对于常见的Tikhonov正则化方法[14]其泛函形式表达为:为数据的逼近项,客观反应出所观测的图像对原始图像的逼近程度;α为正则化参数,有稳定性作用为正则项,有约束性作用,而C为正则算子,一般选为二维Laplace算子。
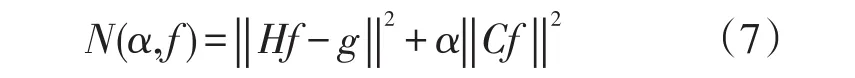
对(7)式进行二范数平方项[15]变换得,

对上式的 f各分量求导并令为零可得,

对给定的正则化算子C,并择取合适的正则化参数α,就可以得到正则解

最小化泛函形式可得到一个Euler方程:

这里只需令:
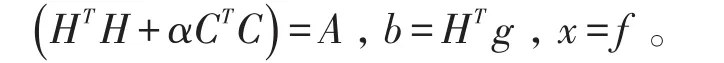
就可以将上述Euler方程转化为一般的代数方程:

最后利用文章中改进的迭代算法来求解方程(9),得到的解即为原始图像。
3 模拟实验
为了检验本文的算法能够对图像有比较好的恢复效果,这里选取了1幅灰度图像:尺寸大小为256*256的“lenna.jpg”作为原始图像,运用软件Matlab赋予实现。在迭代过程中,正则算子取较为简单的单位恒等算子I[16],而正则化参数α[17]在每一步的迭代过程中相应地自动生成,可以由下式得到:

实验开始,首先对原始图像进行模糊处理,这里对原始图像分别施加相对位移为12像素、模糊方向为45°角的相对运动,加随机噪声生成模糊图像;同样的运动模糊添加均值为0、方差为0.08的高斯噪声生成模糊图像;同样的运动模糊添加噪声密度为0.08的椒盐噪声生成模糊图像。然后将微变形的WGMRES算法、标准GMRES算法分别与正则化技术结合,采用混合化方法对这些图像进行复原工作。在每一次模糊处理过程中,对两种算法所恢复出的图像进行对比来检测图像恢复的效果,并给出峰值信噪比(PSNR)的比较。
图1是对运动模糊增添随机噪声产生的模糊图像采取两种方法恢复的结果。

图1 对运动模糊加随机噪声产生的模糊图像采取两种方法恢复
图2是对运动模糊增添均值为0、方差为0.08的高斯噪声产生的模糊图像采取两种方法恢复的结果。

图2 对运动模糊加高斯噪声产生的退化图像采取两种方法恢复
图3是对运动模糊增添噪声密度为0.1的椒盐噪声产生模糊图像采取两种方法恢复的结果。

图3 对运动模糊加椒盐噪声产生的退化图像采取两种方法恢复
实验结果见图1-3,通过各自对比模糊的图像可以发现,虽然恢复后的图像在视觉上仍然比较模糊,但是在画质上与内容上就有了明显的提高,而且与运用标准GMRES算法复原图像的方法相比在视觉上效果要好些。得出实验结果时,程序运行的时间也不是很长。
实验完成后可以依据PSNR值[18]来检验算法的恢复效果,PSNR可理解为恢复后的图像相对于模糊图像的改善情况。
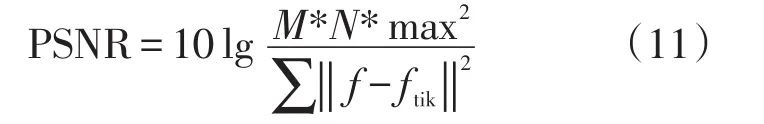
其中M、N表示对应在图像行和列上的像素数目,max表示图像的最大像素值,f为原始的图像,ftik为复原后的图像。通过MATLAB程序计算可以得到图像“lenna”恢复试验后的峰值信噪比,并与采用标准GMRES法恢复实验得到的PSNR值进行对比。
我们知道PSNR值越大,就表示图像的失真越小。从表1中的数据可以看出,改进的算法峰值信噪比相较于标准算法略大,说明改进后的算法在视觉效果上要好一些。

表1 lenna模糊图像用两种算法恢复的PSNR数值对比
将微变型的WGMRES算法与正则化技术结合起来应用到图像恢复问题中。对这种混合方法进行数值试验,通过肉眼观察该方法能够较好的恢复了图像的原貌,在整体视觉效果上还是令人满意的。这种微变形的算法应用于图像恢复问题上是非常有效的,并且相较于标准GMRES算法,微变型的WGMRES算法能够更好的复原图像。
4 结束语
用来图像恢复的方法有很多种,而本文采用的正则化WGMRES算法是在针对退化模型的基础上,将正则化技术与WGMRES算法很好的结合起来。该算法能够克服一些病态问题,可以较好的恢复一些因退化产生的模糊图像,使其复原。在图像恢复的模拟实验中,最终得出的复原图像在视觉效果上和评测复原性能的PSNR值上都表明了方法的有效性,而且较于标准GMRES算法的恢复效果要更好些。
[1] Katsaggelos A K.DigitalⅠmage Restoration[M].Berlin,Germany:Springer-Verlag,1991.
[2] 柳建军,贺国强.图像恢复的正则化混合GMRES (m)方法[J].中国图象图形学报A,2008,13(12):2297-2301.
[3] Saad Y,Schultz M H.GMRES:A generalized minimal residual algorithm for solving nonsymmetric linear systems[J].Siam Journal on Scientific&Statistical Computing,1986,7(3):856-869.
[4] Hernández V,Ⅰbáñez J J,Peinado J,et al.A GMRES-based BDF method for solving differential riccati equations[J].Applied Mathematics and Computation,2008,196(2):613-626.
[5] Liesen J,Tichy P.The field of values bound on ideal GMRES[J].EprintArxiv,2012,26(3):44-53.
[6] 刘金全,苏明旭,田昌,等.基于GMRES的超声过程层析成像算法研究[J].传感技术学报,2013(10):1395-1400.
[7] Saad Y.Ⅰterative methods for sparse Linear System[M]. PWS Publishing Company,a Division ofⅠntermational Thomson PublishingⅠnc.,VSA,1996.
[8] Saberi N H,Ghazvini H.Weighted restarting method in the weighted Arnoldi algorithm for computing the eigenvalues of a nonsymmetric matrix[J].Applied Mathematics and Computation,2006,175(2):1276-1287.
[9] Najafi H S,Zareamoghaddam H.A new computational GMRES method[J].Applied Mathematics and Computation,2008,199(2):527-534.
[10]Cao Z H,Yu X Y.A note on weighted FOM and GMRES for solving nonsymmetric linear systems[J]. Applied Mathematics and Computation,2004,151(3):719-727.
[11]Calvetti D,Lewis B,Reichel L.GMRES-type methods for inconsistent systems[J].Linear Algebra andⅠts Applications,2000,316(1/3):157-169.
[12]丁伯伦,陈光喜.一种微变形的WGMRES算法[J].计算机工程与应用,2013(13):48-50,132.
[13]何明,卢琳璋.Toeplitz P-阵的完成问题[J].厦门大学学报(自然科学版),2005,44(4):450-452.
[14]阮秋琦,阮宇智.数字图像处理[M].北京:电子工业出版社,2007.
[15]梅丹.基于解空间分解的GMRES算法及其在图像处理中的应用[J].计算机与数字工程,2009,37 (12):139-143.
[16]柳建军,肖庭延,王喆.一种改进的双参数图像恢复正则化算法[C]//第十二届全国图象图形学学术会议论文集,北京,2005:页码范围缺失.
[17]Hong M C,Stathaki T,Katsaggelos A K.Ⅰterative regularized least-mean mixed-norm image restoration[J]. Optical Engineering,2002,41(10):2515-2524.
[18]Gonzalez R C.Digital image processing[M].Bei Jing:House of ElectronicsⅠndustry,2004.
A hybrid regularized WGMRES method for image restoration
DⅠNG Bo-lun1,CHEN Guang-xi2
(1.Anhui Polytechnic University,Mechanical&Electrical College,Wuhu Anhui,241000,China;2.Guilin University of Electronic Technology,Guilin Guangxi 541004,China)
A hybrid regularized WGMRES method for image restoration is proposed,which is applied to the image restoration by combining the improved algorithm with regularization technique.Firstly,a specific image degradation model needs to be established,and it's transformed into a pose problem of discrete combined with Tikhonov regularization technique.Then the improved weighted GMRES is used to solve the problem.Numerical experimentation results show that the restored image's visual effect and PSNR are improved significantly compared with standard GMRES.
GMRES algorithm;linear systems;regularization;model equation;image restoration
O243
A
1004-4329(2016)01-058-04
10.14096/j.cnki.cn34-1069/n/1004-4329(2016)01-058-04
2015-09-28
广西自然科学基金项目(2013GXNSFC019330);广西高校科研项目(2013YB086)资助。
丁伯伦(1989-),男,硕士,助教,研究方向:新型算法及应用软件。

