基于遗传算法的嫦娥三号软着陆轨道设计
(阜阳师范学院 a.数学与统计学院;b.物理与电子工程学院,安徽 阜阳 236037)
孙娓娓a, 张开银b
基于遗传算法的嫦娥三号软着陆轨道设计
(阜阳师范学院 a.数学与统计学院;b.物理与电子工程学院,安徽 阜阳 236037)
嫦娥三号是我国航天器首次在地外天体的软着陆和巡视勘探,而软着陆又是所有探测月球活动中最为关键的技术。该文利用飞行器动力学方程和能量守恒定律得出有关燃料和时间的方程。然后将遗传算法应用于着陆轨道的优化设计,通过MATLAB程序实现,给出了飞行状态和控制变量的仿真结果,得到了燃料最优的软着陆轨道。仿真结果表明,遗传算法可搜索到全局最优的着陆轨道。并对所得的制导轨道进行误差估计和敏感性分析。
软着陆;遗传算法;嫦娥三号;敏感性
当今地球资源日益匮乏,很多国家把目光从地球转向了月球。我国的探月工程起步比较晚,但是在许多方面取得了不小的成就。2013年12 月6日,嫦娥三号顺利进入环月轨道,登月器在月球上的预定着陆点为虹湾以东地区19.51W,44.12N,海拔-2 641 m。探月器在高速飞行的状况下,如果要保证其准确地在月球预定区域内实现软着陆,着陆轨道是关键问题。本文针对嫦娥三号软着陆问题,通过利用动力学原理和遗传算法相关知识,对着陆轨道进行优化控制,并对其结果进行灵敏度分析。
1 基于遗传算法的着陆轨道设计
嫦娥三号着陆轨道的基本设计要求是:着陆准备轨道为近月点15 km,远月点100 km的椭圆形轨道;着陆轨道为从近月点着陆点,其软着陆过程共分为6个阶段,在这些阶段中要满足关键点所处的状态,同时还要最大的减少软着陆过程的燃料消耗。当探测器在其椭圆轨道上运行到近月点时,发动机再次启动,为的是减少探测器的速度;在靠近月球表面时,探测器为以降低着陆撞击为目的,直到安全完成软着陆[1]。
孙娓娓a, 张开银b
为了确定嫦娥三号的着陆轨道,很多文献都采用了传统的优化算法,优化的结果对某些参数的初始值非常敏感。由于遗传算法[2]具有很强的全局寻优能力,因此很多学者应用它来研究太空探测。本文采用基于浮点数编码的遗传算法[3]设计月球软着陆轨道。
1.1动力学模型
由于月球表面没有大气层,而且从15 km的轨道软着陆所用时间比较短,所以大气阻力项、月球引力非球项、日月引力摄动等影响因素可忽略不计。这里采用惯性坐标系下的二体模型[4]来建立探测器的动力学方程[5],如图1所示。

图1 探测器二体模型示意图

其中vr、vθ是探测器的法向速度和切向速度;μ是月球引力常数;r是月心距;a是推力加速度;β是推力方向角,即推力方向与当地水平线的夹角;θ是极角。
探测器着陆满足的初始条件为:

其中初始切向速度vθ0并不是当地的环绕速度,而是探测器从远月点运动到近月点的速度,这一速度大于当地环绕速度,Δvk就是这两个速度的差;由于飞行器的初始时刻在近月点,所以初始法向速度vr0=0;初始轨道半径r0为近月点,aL为月球半径,h为轨道高度。
探测器着陆满足的终止条件为:

即当探测器落到月球表面时,其速度为0。而对于整个软着陆过程,追求的目标是燃料消耗达到最小[6],即

其中Isp为发动机比冲;g为重力加速度;tf为软着陆完成时刻。
1.2遗传算法
上节中所建立的探测器的物理模型,在数学上本质就是一个带约束的优化问题,其目标函数就是求式(4)所描述的燃料消耗的最小值。需要优化的参数包括(1)式中的4个状态变量vr、vθ、r、θ在初始时刻和终止时刻的值、1个飞行时间变量t、1个推力变量T,共10个参数;这些参数应满足以下8个约束条件,其数学模型如下:


针对上述数学优化问题利用浮点数编码的遗传算法进行求解,步骤如下:
Step1:随机产生N个长度为n(优化参数的个数)的浮点数编码组成初始种群;
Step2:按(4)式计算种群中每个个体的适应度值,采用轮盘赌方式进行选择操作,同时将最佳个体直接保留到下一代;
Step3:将个体随机两两配对,按照指定的概率Pc进行算术交叉操作;
Step4:对选中的父代个体,按照指定概率Pm进行均匀变异操作,得到下一代种群;
Step5:若连续若干代的最优个体的适应值不再提高,则终止算法,并输出最优个体;否则转Step2。
2 仿真结果
以2014年全国大学生数学建模竞赛A题相关数据为例,初始时刻的探测器质量m0=2.4×103kg,发动机比冲Isp=2 940m/s,发动机推力限制在1 500~7 500N。探测器轨道高度h=15km,初始时刻切向速度为1.691 8 km/s,法向速度vr0=0;终止时刻探测器降落在月球上,rf=aL=1 738km,速度vrf=0,vθ=0。
遗传算法的相关参数为:优化参量的数目n= 10,种群规模N=20;交叉概率Pc=0.6,变异概率pm=0.05,迭代次数Titer=1 000。
利用Matlab软件,计算出探测器着陆飞行总时间为721.67 s,并画出了软着陆过程中推力方向角、月心距、极角、径向速度随时间变化的曲线图,如图2所示。

图2 轨道参数变化曲线
从图2可以看出,月心距、推力方向角都一直在减小;而径向速度沿指向月心方向,先增大后减小,其最大值达到45m/s;极角θf-θo=6.30°。
3 着陆轨道敏感性分析
本文所设计的着陆轨道是在理想状态下所得到的,即不考虑导航误差、姿态控制误差以及各种系统误差的情况[7]。但在探测器发射过程中,嫦娥三号运行轨道是受很多因素影响制约的,若这些因素产生扰动,就不能保证精确到达预着陆点。因此,对着陆轨道进行敏感性分析是很有必要的。
3.1初始质量估计误差
初始质量增加5%的误差,推力方向角、月心距、极角、径向速度仿真结果如图3所示。可以看出,着陆精度不满足1 km的要求,这是因为增加质量会使推力加速度减小,造成最小航程增大,从而引起较大的着陆误差[8]。由于质量误差带来的航程偏差是无法量化的,因此可以引入推力开关函数来调整航程,从而到达着陆区域。

图3 初始质量引起轨道参数偏差情况
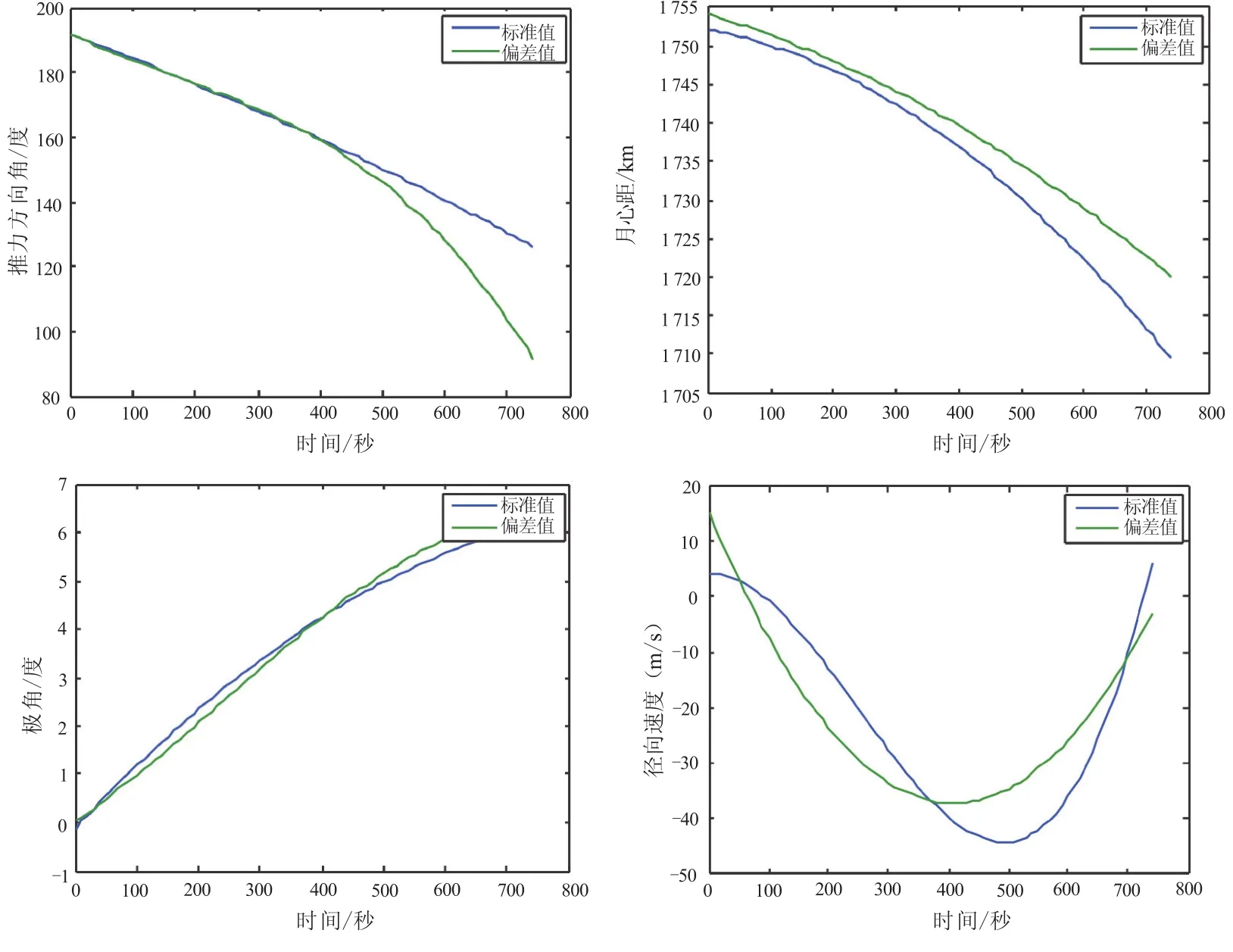
图4 推力大小引起轨道参数偏差情况
3.2推力大小误差
推力增加3%的误差,推力方向角、月心距,极角,径向速度仿真结果如图4所示。从仿真结果上看,除极角外,其他轨道参数对推力的大小都很敏感,故推力的偏差对着陆的影响比较大,因此需要对发动机的推力提出更高的精度。
4 结束语
本文采用遗传算法来确定嫦娥三号的着陆轨道,很好的确保了飞行器的安全问题。遗传算法对参数的不依赖性和全局优化性大大地提高了结果的准确性和可靠性。本文所设计的着陆轨迹模型不仅仅适用于航天事业,也可以运用到其他领域,如地质探测等[9],使用价值高,实用性强。
[1] 蒋瑞,韩兵.嫦娥三号着陆控制研究与软件仿真[J].微型电脑应用,2012,28(2):17-19,34.
[2] 李琳琳.遗传算法在控制中的应用[D].哈尔滨:哈尔滨工业大学,1998:78-81.
[3] 张彤,张华,王子才.浮点数编码的遗传算法及其应用[J].哈尔滨工业大学学报,2000,32(4):59.
[4] 刘暾.空间飞行器轨道动力学[M].哈尔滨:哈尔滨工业大学出版社,1991:173-175.
[5] Pierson BⅠ,Kluever C A.Three-stage approach to optimallow-thrust earth-moon trajectories[J].Guidance,Control,and Dynamics,1994,17(6):1275-1282.
[6] Noton M.现代控制理论[M].北京:科学出版社,1979:25-26.
[7] 王劼,崔乃刚,刘暾,等.定常推力登月飞行器最优软着陆轨道研究[J].高技术通讯,2003,13(4):39-42.
[8] Ueno S,Yamaguchi Y.3-Dimensional near-minimum fuel guidance law of a lunar landing module[J].AⅠAA Journal,1999,39(3):248-253.
[9] Mcinnes C R.Path shaping guidance for terminal lunar descent[J].Acta Astronautica,1995,36(7):367-377.
Soft landing orbit design of Chang'e No.3 based on genetic algorithm
SUN Wei-weia,ZHANG Kai-yinb
(a.School of Mathematics and Statistics;b.School of Physics and Electronic Engineering,Fuyang Normal University,Fuyang Anhui 236037,China)
Chang'e No.3 is the soft landing and tour exploration to the extraterrestrial objects for the first time.Soft landing is the most important part of all exploration for the moon.This paper gets equation about fuel and time using vehicle dynamics equation and the law of energy conservation.Then genetic algorithm is applied to the optimization design of landing orbit. Through MATLAB implementation,the simulation results of the flight state and control variables are given.The fuel optimal soft landing orbit is obtained.The simulation results show that genetic algorithm can search the global optimal landing orbit.Finally the error estimation and sensitivity analysis of the orbit are made.
soft landing;genetic algorithm;Chang'e No.3;sensitivity
V474.3
A
1004-4329(2016)01-011-05
10.14096/j.cnki.cn34-1069/n/1004-4329(2016)01-011-05
2015-09-30
安徽高校省级自然科学研究项目(2015KJ003);教育部留学回国人员科研启动基金资助(2012-42);安徽省质量工程项目(2013zy167,2014zy138,2015jxtd121);阜阳师范学院质量工程项目(2013ZYSD05,2014JXTD01)资助。
孙娓娓(1981-),女,硕士,讲师,研究方向:智能计算。

