局部有界函数的Picard算子收敛阶的估计
沈晓斌,黄东兰
(1泉州师范学院 数学与计算机科学学院,福建 泉州 362000;2智能计算与信息处理福建省高等学校重点实验室,福建 泉州 362000)
局部有界函数的Picard算子收敛阶的估计
沈晓斌1,2,黄东兰1,2
(1泉州师范学院 数学与计算机科学学院,福建 泉州 362000;2智能计算与信息处理福建省高等学校重点实验室,福建 泉州 362000)
对局部有界函数 f的Picard算子在区间(-∞,+∞)上的收敛阶进行估计。在蔡清波等人关于Picard算子的收敛阶研究基础上,对其所给的估计结果作进一步改进,得到更精确的系数估计。
局部有界函数;Picard算子;收敛阶;Laplace分布
文[1]主要研究了定义在区间(-∞,+∞)上局部有界可积函数f的Picard算子收敛于的收敛阶,得到其收敛阶的估计。本文在此基础上进一步讨论文[1]关于Picard算子,注意到其基函数与Laplace分布的关系,利用概率性质等方法,通过估计相关函数关于Laplace分布的数学期望,从而给出了更好的估计式。关于概率型算子逼近理论的研究可参考文[2-8]。为了便于叙述,本文采用与文[1]相同的符号。先介绍Picard算子、相关的函数类及一些引理。
1 定义和引理
定义1设 f是定义在(-∞,+∞)上的可积函数,且满足如下增长阶:,称
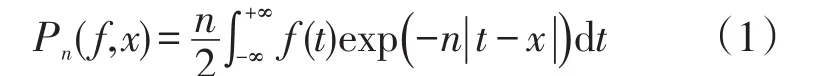
为 Picard算子。当核函数 Kn(x,y)定义为t, 则算子Pn(f,x)可以表示为Lebesgue-Stieltjes的积分形式

定义3局部有界函数类ΦB定义为ΦB={f| f在[0,∞)的每个有限子区间是有界的}。
定义4局部有界变差函数类BVloc(-∞,+∞)定义为BVloc(-∞,+∞)={f|f在(-∞,+∞)的每个有限子区间为有界变差}。
引理1设随机变量ξ服从参数为(n-1,x)的Laplace分布,则随机变量函数
φ(ξ)=(ξ-x)2exp()βξ,当x∈(-∞,+∞)及n>2β时的数学期望:

证明
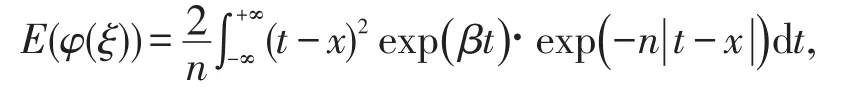
作变量代换t-x=u,则
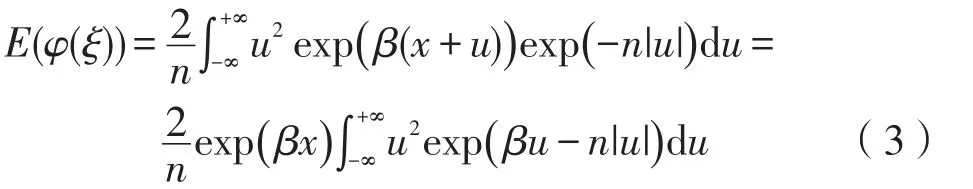
又
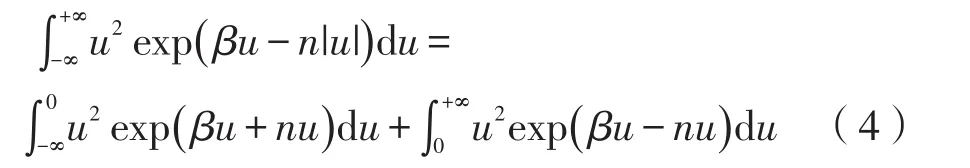


式(5)和式(6)代入式(4),注意到n>2β则n3>4nβ2,得

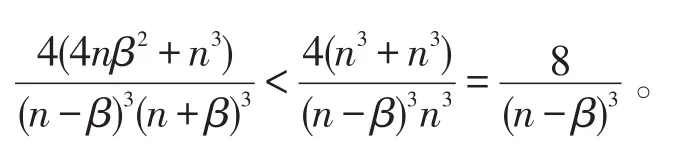
所以由式(6)知
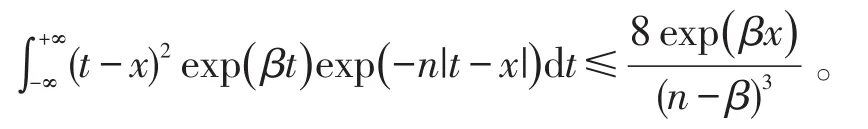
即
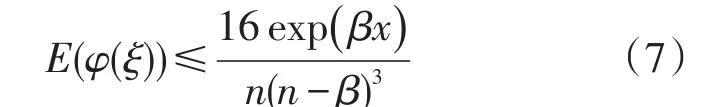
引理2当n>3+β(β>0)时有

证明 由于式(8)等价于16n2(n-2β)(n+2β)<6(n-β)6,即

令α=n-β代入式(9)并整理,

又,由均值不等式,
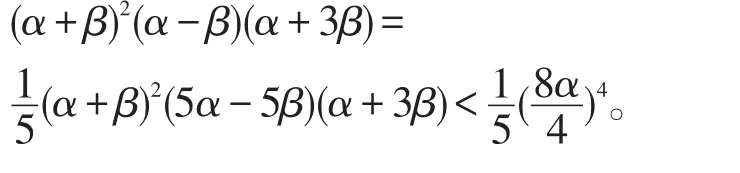
整理得

2 Picard算子的收敛阶
Picard算子关于局部有界函数类有如下的收敛阶:
定理1[1]设 f是满足如下条件的函数,f∈ΦB, |f(t)|≤Mexp()βt(M>0;β≥0;t→∞),若f(x+)和 f(x-)在定点 x∈(-∞,+∞)存在,则当n>2β时,有

其中,[n]表示不超过n的最大整数,
收集天津某三级甲等综合性大学医院近年来医院接待中心、医保办公室(简称医保办)、便民服务热线、医患沟通座谈会、意见箱、第三方满意度调查中涉及医保相关投诉内容作为PDCA循环管理的依据。


其中gx(t)和[n]同前述定义。
由定理1和定理2,我们依次可以得到Picard算子关于局部有界变差函数类的收敛阶:
推论1[1]设 f是满足如下条件的函数,f∈BVloc, |f(t)|≤Mexp()βt(M>0;β≥0;t→∞),若f(x+)和 f(x-)在定点 x∈(-∞,+∞)存在,则当n>2β时,有
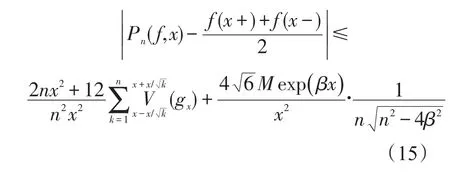

3 定理2的证明
设 f∈ΦB,对所有的t有:
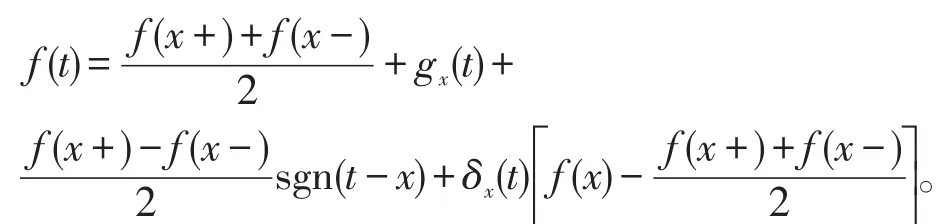
这里,gx(t)如式(13)所定义,
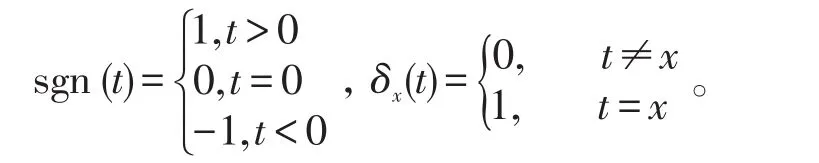
由Pn(1,x)=1,可得
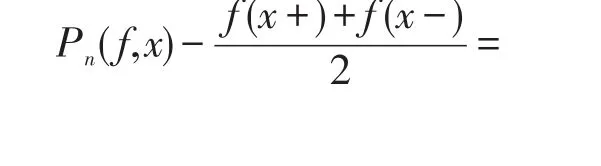


从而


其中,
则
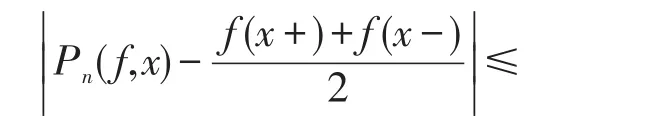

文[1]已经给出
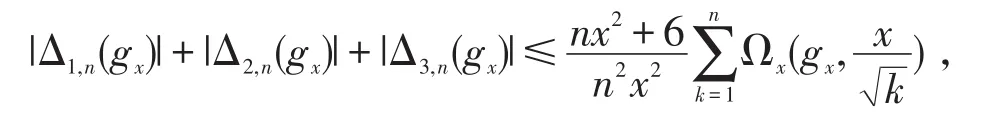
则

所以只需对式(18)的|Δ4,n(gx)|重新估计,由于

t≥2x⇒||t-x≥||x。从而
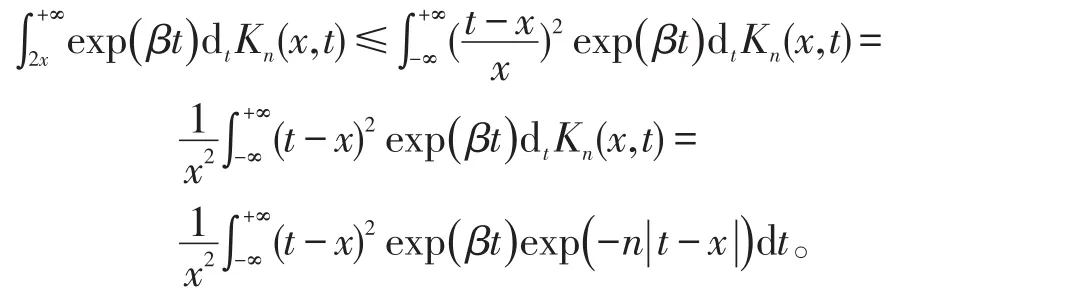
即

由引理1的结果代人式(21)得
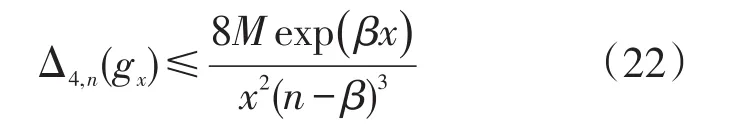
把式(22)代入式(19),定理2得证。
4 结束语
比较式(12)和式(14)右端的第二项,由引理2的式(8)得当n>3+β(β>0)时。两个收敛阶的估计式有如下关系:
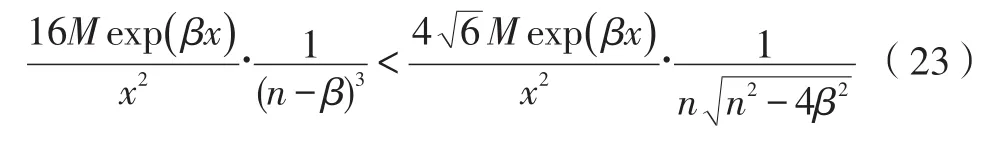
更何况
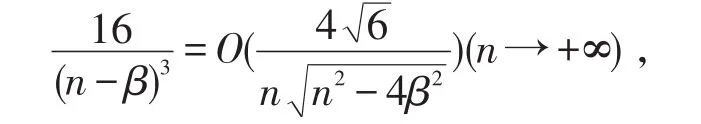
即式(14)的收敛阶高于式(12)。相应地,推论2优于推论1。
从而,本文所得的局部有界函数Picard算子的收敛阶的估计优于文[1]的估计。但是,本文改进的这一项并不是主项,所以最终的估计对整体没有本质的影响,笔者将进一步探究对另一项的改进以达到更有意义的结果。虽然本文对结果的贡献不显著,但在于提出运用概率论的有关性质来研究算子逼近论,该方法的运用或许将有助于对于一系列诸如Gamma算子[2]等概率型算子收敛阶的进一步优化。
[1] 蔡清波.Picard算子对局部有界函数的逼近[J].泉州师范学院学报,2011,29(2):43-45,64.
[2] Zeng X M.Approximation properties of Gamma operators[J].Journal of Mathematical Analysis and Applications,2005,311(2):389-401.
[3] Bojanic R,Cheng F H.Rate of convergence of Bernstein polynomials for functions with derivatives of bounded variation[J].Journal of Mathematical Analysis andApplications,1989,141(1):136-151.
[4] 王平华.Szász算子的收敛速度的估计[J].阜阳师范学院学报(自然科学版),2001,18(3):9-10,39.
[5] 黄坤阳.ⅠntegraⅠ型Lupas-Bézier算子收敛阶的估计[J].巢湖学院学报,2015,17(3):12-15.
[6] Wang P H.Cai Q B and Li Z W.estimate on rate of convergence of the integral type Lupas-Bézier operators [J].Far East Journal of Mathematical Sciences,2008,28(1):189-196.
[7] 王平华,沈晓斌.有界变差函数的Szasz-Bézier算子收敛阶的估计[J].黄冈师范学院学报:自然科学,2005,25(6):1-3,8.
[8] 黄东兰,王平华.Durrmeyer-Bézier算子收敛阶的新估计[J].泉州师范学院学报,2014,32(6):86-88,116.
[9] 陈争鸣,王平华.Picard算子对绝对连续函数的新收敛阶[J].江西科技师范大学学报,2014,13(6):43-47.
[10]黄东兰.局部有界函数的Baskakov-Bézier算子收敛阶新的估计[J].三明学院学报,2014,32(6):11-14.
Estimate on rate of convergence of Picard operators for locally bounded functions
SHEN Xiao-Bin1,2,HUANG Dong-lan1,2
(1.School of Mathematics and Computer Science,Quanzhou Nomal University,Quanzhou Fujian 362000,China;2.Fujian Provincial Key Laboratory of Data Intensive Computing,Quanzhou Fujian 362000,China)
Ⅰn this article we estimate the rate of convergence of Picard operators for locally bounded functionfon(-∞,+∞).Our study is based on the authors Cai and the others′researches about the rate of convergence of Picard operators,and improves the results of estimation,gets more accurate coefficient estimation.
locally bounded functions;Picard operators;rate of convergence;Laplace distribution
O174.41
A
1004-4329(2016)01-018-04
10.14096/j.cnki.cn34-1069/n/1004-4329(2016)01-018-04
2015-09-15
福建省中青年教师教育科研项目(JA14262)资助。
沈晓斌(1966-),男,本科,副教授,研究方向:算子逼近论。
——以广西现代职业技术学院为例
——泉州宋船

