横看成岭侧成峰多元角度探本质——以一类数列问题为例

杨碧明，刘永杰



横看成岭侧成峰多元角度探本质——以一类数列问题为例

杨碧明，刘永杰

(阜阳市第一中学，安徽 阜阳 236000）

文章以安徽省2012年理科数学高考压轴题为例，运用不动点理论以及函数单调性研究了与收敛递推数列有关的单调性问题并给出了这类问题几何意义，从而总结出了解决这类问题的一个有效方法。

递推数列；不动点；几何意义

数列是高中数学的主干知识之一，高考中数列题主要考查性质，数列常与函数、不等式，数学归纳法等知识融合在一起，这些问题整合程度高、难度大，常用来命制压轴题。2012年安徽理科数学第21题对于绝大多数高中学生而言是个严峻的挑战，这个题目难度很大，便是这样的命题思路。高三复习过程中我们应该引导学生从事物的特殊问题出发来探究一般问题，来揭示事物的背景和本质。

1 题目背景

证明：（Ⅰ）略

2 背景揭示

上面的解题过程是安徽省考试院给出的参考答案，从上面的解题过程中可以看出运用递推数列的性质首先得到的取值范围是第一个难点，而在(2)式中两边同时减去，涉及到了高等数学中的不动点理论，学生也不容易想到。

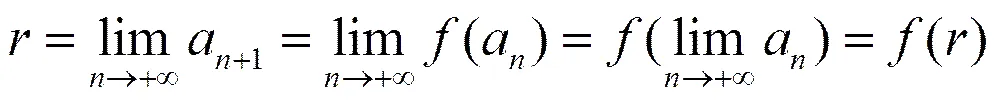
基于上面的理论分析在此基础上还可以给出下面解法

在上恒成立，下略。

以上那种方法是解决本题的一般方法呢？下面给出本题的几何意义。

3 几何意义

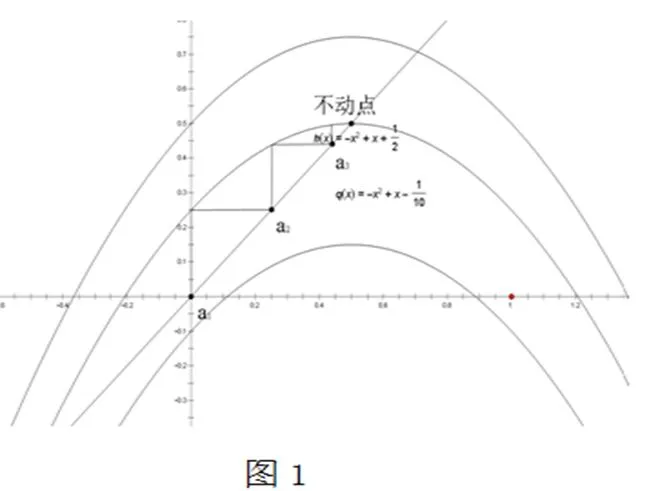
由上述分析可知这个问题本质上是一个不动点问题，本题的几何意义为在同一坐标系中画出和的图像，并在图像上取点将对应到直线上，对应关系如下图。这样就能在图上清晰的看到数列的单调性，即可以得到，最后再结合函数单调性运用数学归纳法证明结论成立，如图1所示。

4 总结

此类收敛递推数列单调性问题的解决方法主要有

（1）借助此类数列的几何意义，即在同一坐标系中画出数列对应的函数图像和直线的图像，再在直线上取符合题意的初始点设为，再利用函数图像及其性质将对应到直线上，即可得到一个初步结论。若要证明这个结论只需要构造函数几何图形及函数单调性运用数学归纳法证明即可。

请读者根据几何意义写出完整步骤。

附练习1，练习2，第（Ⅱ）问几何意义如分别如图2，图3

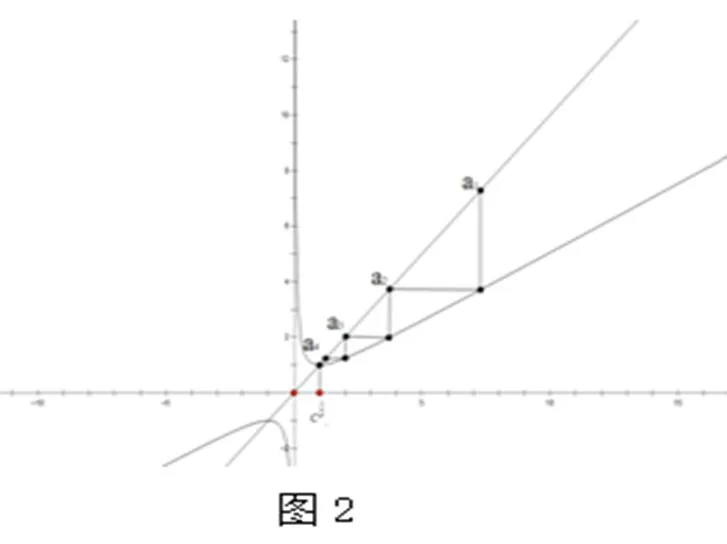
同样函数压轴题具有综合性强、解法灵活多变等特点，从近几年的高考题可以看出，所考查的函数都是基本初等函数的组合，如函数等。如果我们能够将这些常用函数模型的图像总结出来，可以使学生见到该类问题不感到陌生，快速找到解题的突破口，同时提高了学生解题的高度。

数学题千变万化，呈现形式多种多样，但我们只要用心领悟数学思想方法，把握数学问题本质，理解数学问题所隐含几何意义，很好勾勒出各环节中函数的图像，就能使问题形象化，复杂问题简单化，更为重要的是要让数学基本思想、基本方法指导我们的思维和解题过程。

[1]裴礼文.数学分析中的典型问题与方法[M].北京：高等教育出版社,1998:34-48.

[2]陈传理,张同君.竞赛数学教程[M].北京：高等教育出版社，2010.

2016-09-29

杨碧明(1969-)，女，安徽天长人，阜阳市第一中学高级教师。主要研究方向：数学教育。

G634.6

A

1672-4437（2016）04-0106-03