VALUE-AT-RISK AND CONTINUOUS COHERENT RISK MEASURES ON LP-SPACE

CHEN Yan-hong，HU Yi-jun

(School of Mathematics and Statistics，Wuhan University，Wuhan 430072，China）

VALUE-AT-RISK AND CONTINUOUS COHERENT RISK MEASURES ON LP-SPACE

CHEN Yan-hong，HU Yi-jun

(School of Mathematics and Statistics，Wuhan University，Wuhan 430072，China）

In this paper，we study the relation between value-at-risk and continuous coherent risk measures on Lp-space.By using the separation theorem for convex sets and the truncated approximation method，we obtain that VaR can be represented by continuous coherent risk measures on Lp-space.Meanwhile，we get a new method to prove the representation result for the continuous coherent risk measures on Lp-space，which extend the results in［2］from L∞-space to Lp-space，and do some complements of that of Inoue［4］，respectively.

Lp-space；continuous coherent risk measures；value at risk

2010 MR Subject Classification：62P05；91B30

Document code：AArticle ID：0255-7797（2016）05-1011-08

1 Introduction

Artzner et al.［1-2］first proposed the concept of coherent risk measures.Further，Delbaen［3］studied coherent risk measures on general probability spaces.Value-at-risk（VaR）is a popular risk measure，especially in practice.However，VaR is not of subadditivity. Artzner et al.［2］and Delbaen［3］provided expressions for VaR in terms of kinds of coherent risk measures on L∞-space.

Coherent risk measures on Lp-space，1≤p＜∞，were also studied in the literature，for example［4-9］.A natural and interesting issue is how about the relation between VaR and coherent risk measures on Lp-space.So far，we have not found any report on this issue.In this paper，we will provide an expression for VaR in terms of kinds of continuous coherent risk measures on Lp-space.Meanwhile，we also give a proof of the representation result for continuous coherent risk measures on Lp-space.It should be mentioned that Inoue［4］stated the representation for continuous coherent risk measures on Lp-space，1≤p≤∞，but only the proof in L∞-space case was provided.It is well-known that the dual spaces of L∞and Lp（1≤p＜∞）are quite distinct.The proof of the representation result for continuous coherent risk measures on Lp-space（1≤p＜∞）deserves to be provided.The proof provided in this paper is different from that of Inoue［4］.

The rest of the paper is organized as follows.In Section 2，we will introduce preliminaries.The main results will be stated in Section 3.Finally，in Section 4，the proofs of the main results are given.

2 Preliminaries

In this section，we will briefly introduce the preliminaries.Let（Ω，F，P）be a fixed probability space.We denote H=Lp（Ω，F，P）for 1≤p≤+∞.When 1≤p＜+∞，H is the space of random variables with finite p-order moment.L∞（Ω，F，P）stands for the space of all essentially bounded random variables on（Ω，F，P）.The space H represents financial risk positions.Positive values of X∈H correspond to losses，while negative values correspond to gains.For X∈H，define‖X‖p：=essup|X|，if p=+∞，if 1≤p＜∞，where EP（|X|p）means the integral of|X|pwith respect to the probability P，then（H，‖.‖p）is a Banach space.For 1≤p＜∞，q means the conjugate index of p,=1（q=∞if p=1）.

We introduce more notations.Denote by M1（P）the set of P-absolutely continuous probability measures on（Ω，F，P）.For X∈H，we set X∧n：=min（X，n），X+：=max（X，0）and X-：=max（-X，0）.Given a set A，1Ameans the indicator function of A.

In general，a risk measure is defined as any function ρ from H to the real numbers R. Given a position X∈H，the quantity ρ（X）is interpreted as the amount of risk capital that the holder of position X has to safely invest，in order to satisfy the regulator.

Definition 2.1（see［4］）A risk measure ρ：H→R is called a coherent risk measure，if it satisfies the following four axioms

（A1）Monotonicity：X≥Y implies ρ（X）≤ρ（Y）for any X，Y∈H.

（A2）Translation invariance：ρ（X+a）=ρ（X）-a for any X∈H and a∈R.

（A3）Positive homogeneity：ρ（λX）=λρ（X）for any X∈H and λ≥0.

（A4）Subadditivity：ρ（X1+X2）≤ρ（X1）+ρ（X2）for any X1，X2∈H.

We call that a coherent risk measure ρ：H→R is continuous，if

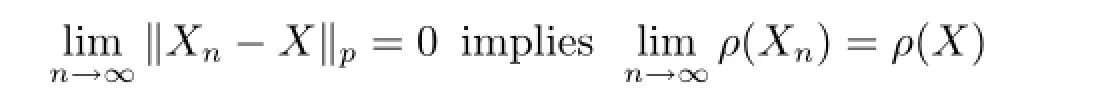
for any Xn，X∈H.

Remark 2.1 Given a coherent risk measure ρ：H→R，ρ is continuous if and only if there exists C∈（0，∞）such that|ρ（X）|≤C‖X‖p（see［4］）.

Definition 2.2（see［3］）If X is a real-valued random variable and α∈（0，1），then we say that qα（X）is an α-quantile of X if P［X＜qα（X）］≤α≤P［X≤qα（X）］.

It is easy to see that the set of quantiles forms a closed interval with endpointsand.These endpoints can be defined as

Definition 2.3（see［10］）The quantity V aRα（X）：=（X）is called the value at risk at level α for the random variable X.

Definition 2.4（see［11］）Two random variables X and Y are called comonotonic，if there is no pair（ω1，ω2）in some Ω0with P（Ω0）=1 such that X（ω1）＜X（ω2）and Y（ω1）＞Y（ω2）.

Definition 2.5（see［11］）A risk measure ρ：H→R is called to be of comonotonic additivity，if for all comonotonic X1，X2∈H，we have ρ（X1+X2）=ρ（X1）+ρ（X2）.

3 Main Results

In this section，we will state the representation result for continuous coherent risk measures on H，and the relation between VaR and continuous coherent risk measures on H.

Theorem 3.1Let 1≤p＜∞.For a risk measure ρ：H→R，the following conditions are equivalent：

（1）The risk measure ρ is a continuous coherent risk measure.

（2）There exists a set G of nonnegative random variables g with EP［g］=1 such that

for any X∈H.

for any X∈H.

Remark 3.1The statement of Theorem 3.1 can also be found in Inoue［4］.However，Inoue［4］gave only the proof for X∈L∞.In this paper，we will complement the proof for the case of X∈Lp（Ω，F，P），1≤p＜∞.

Now，we are in a position to state another main result of the present paper，which is a generalization of Proposition 5.2 in Artzner et al.［2］and Theorem 6.8 in Delbaen［3］.

Theorem 3.2Let 1≤p＜∞.For every X∈H and any α with 0＜α＜1，we have VaRα（X）=inf｛ρ（X）：ρ is a continuous coherent risk measure on H and ρ≥VaRαon H｝.

4 Proofs of Main Results

In this section，we will provide proofs of Theorems 3.1 and 3.2.

First，we will adopt the dual method to prove Theorem 3.1，which can also be seen in Yan［11］.

Proof of Theorem 3.1（2）⇔（3）follows form the Randon-Nikodym theorem.

（2）⇒（1）is also obvious.Hence，it suffices to prove（1）⇒（2）.To do this we only need to show that for any X∈H，there exists gX∈Lq（Ω，F，P），such that

and

for all Y∈H hold.

In fact，by（4.1）and（4.2），we have

for all X∈H，where G：=｛gX：X∈H｝.

By the translation invariance of ρ，with no loss of generality，we can assume that ρ（X）= 1.Since ρ is a continuous coherent risk measure，by Remark 2.1，there exists C∈（0，∞）such that ρ（X）≤C‖X‖pfor all X∈H.

Let

Then B1⊂B，X/∈B.Since B is a convex set，by the Hahn-Banach theorem，there exists a nontrivial h∈Lq（Ω，F，P），such that

where h（-X）：=EP［（-X）h］.Obviously，B1⊂B，h（-X）＞0.As a result，we can choose h such that h（-X）=1.We further claim that h has the following three properties

（1）h（Y）≥0 for any Y≥0，Y∈H.

（2）h（1）=1.

（3）h（-Y）≤ρ（Y）for any Y∈H.

First，we prove（1）.For any Y≥0，Y∈H and any s＞0，sY∈B.Hence h（-sY）≤h（-X）=1.By arbitrariness of s＞0，we conclude that h（Y）≥0.From property（1）we obtain that h is a nonnegative random variable.

Second，we prove（2）.On one hand，for any-1＜s＜0，s∈B.Then h（-s）≤h（-X）= 1，which implies h（1）≤1，because-1＜s＜0 is arbitrary.

Finally，we prove（3）.For any Y，let Y1：=Y+ρ（Y）-1，then for any s＞1，∈B， which implies h（-Y1）≤1，because s＞1 is arbitrary.Hence h（-Y）≤ρ（Y）.From the choice of h and property（3），we obtain（3.2）.

Next，we will prove（3.1）.Note that ρ is continuous，for any X∈H，

which yields for all g∈G，

Next，we will borrow the idea of the proof of Artzner et al.［2，Proposition 5.2］to prove Theorem 3.2.However，more lemmas and more delicate arguments will be needed.Let us begin with lemmas.

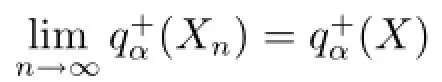
ProofObviously，Xn↑X and Xnis an increasing sequence and）is an upper bound of）.That is，

for any n≥M.Hence

Similarly，one can steady show the following lemma.

Lemma 4.3Let 1≤p＜∞，ρ be a continuous coherent risk measure on Lp（Ω，F，P）and the set Δ be as in（3.3）and（3.4），then ρ≥V aRαon Lp（Ω，F，P）if and only if for every B with＞α and any ε＞0，there is a measureµ∈Δ withµ（B）＞1-ε.

Proof（1）Necessity：For any ε＞0 and any B with P（B）＞α，since

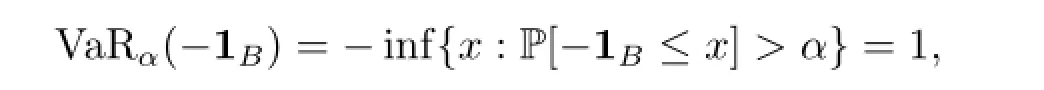
we have ρ（-1B）≥1.This implies that there exists a measureµ∈Δ withµ（B）＞1-ε.

（2）Sufficiency：First，we consider the case where X∈Lp（Ω，F，P）is bounded.

Given a bounded random variable X and any ε＞0，let，whereThen＞α.So there exists a measureµ∈Δ such thatµ（B）＞1-ε. Hence，

Taking into account the fact that

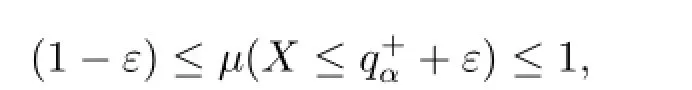
we claim that

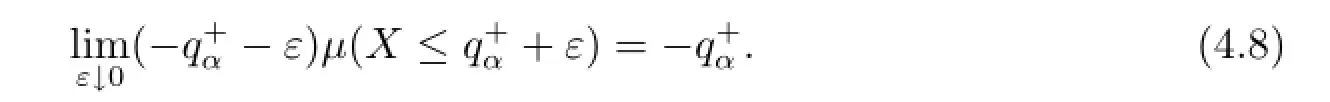
which yields（4.8）by letting ε→0.

which also yields（4.8）by letting ε→0.

Combining（4.7）and（4.8）gives rise to

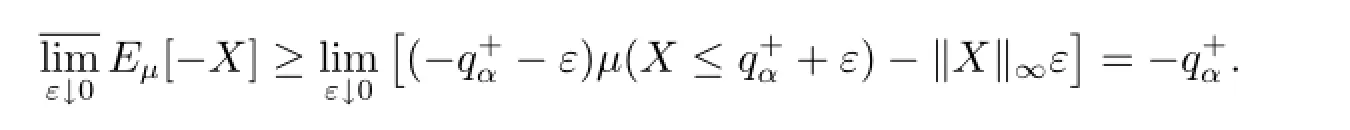
Therefore

Next，let us consider the general case where X∈Lp（Ω，F，P）.Let：=X+∧n，andX andX‖p=0.It is easy to see thatandare comonotonic，as well as X+and X-.From Lemmas 4.1，4.2 and the comonotonic additivity of VaR it follows that

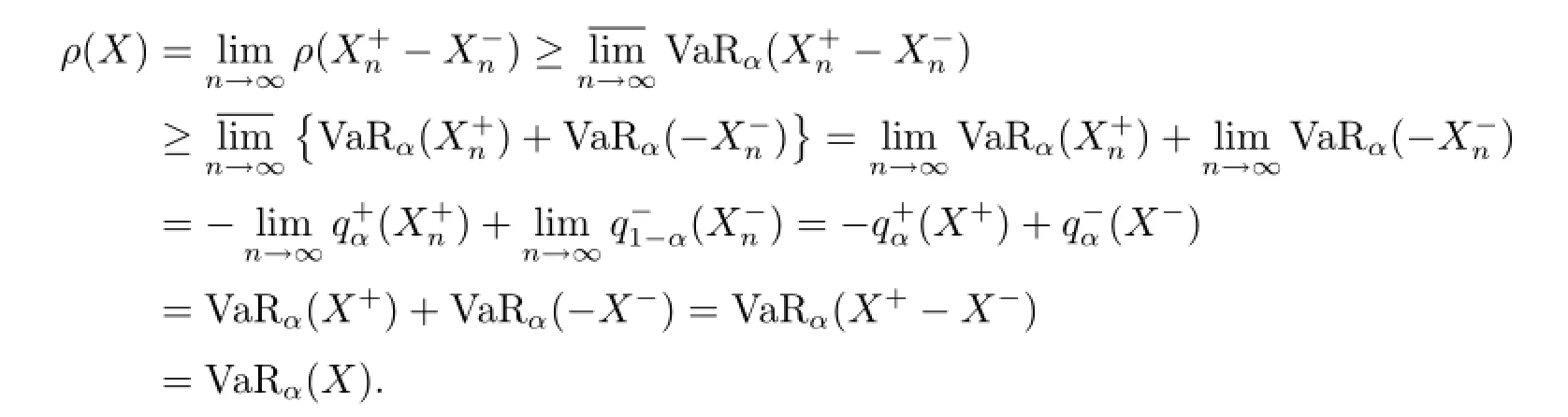
The proof of Lemma 4.3 is completed.

Next，we will use Proposition 3.1 and Lemma 4.3 to prove Theorem 3.2.

Proof of Theorem 3.2We only need to show that for given X∈H，there is a continuous coherent risk measure ρXsuch that ρX≥VaRαon H and with the property that ρX（X）≤VaRα（X）.

Let

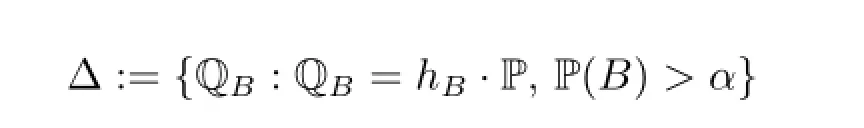
and define a risk measure ρX：H→R by

By Proposition 3.1 and Lemma 4.3，we know that ρXis a continuous coherent risk measure on H，and ρX≥VaRαon H with the property that ρX（X）≤（X）=VaRα（X）.The proof of Theorem 3.2 is completed.

References

［1］Artzner P，Dellbaen F，Eber J M，Heath D.Thinking coherently［J］.Risk，1997，10（4）：68-71.

［2］Artzner P，Dellbaen F，Eber J M，Heath D.Coherent measures of risk［J］.Math.Finan.，1999，9（3）：203-228.

［3］Delbaen F.Coherent risk measures on general probability spaces［J］.Adv.Finan.Stoch.，2002，35（2）：1-37.

［4］Inoue A.On the worst conditional expectation［J］.J.Math.Anal.Appl.，2003，286（1）：237-247.

［5］Fischer T.Risk capital allocation by coherent risk measures based on one-sided moments［C］.Insur. Math.Econ.，2003：135-146.

［6］Nakano Y.Efficient hedging with coherent risk measure［J］.J.Math.Anal.Appl.，2004，293（1）：345-354.

［7］Hamel A H，Heyde F.Duality for set-valued measures of risk［J］.Siam J.Finan.Math.，2010，1（1）：66-95.

［8］R¨uschendorf L.Mathematical risk analysis［J］.Berlin：Spring，2013.

［9］Wei Linxiao，Hu Yijun.Coherent and convex risk measures for portfolios with applications［J］.Stati. Prob.Lett.，2014，90（7）：114-120.

［10］Li Yongming，Zhang Wenting，Cai Jipan.The asympotic properties of the sample quantile estimator of VaR under postitive associated samples［J］.J.Math.，2015，35（2）：13-20.

［11］Yan，Jiaan.An introduction to the financial mathematics［M］.Beijing：Chinese Academic Press，2012.

在险值与Lp-空间上的连续一致风险度量

陈燕红，胡亦钧
（武汉大学数学与统计学院，湖北武汉430072）

本文研究了在险值和Lp-空间上的连续一致风险度量之间的关系.利用凸集分离定理和截尾逼近方法，获得了在险值可以用Lp-空间上的连续一致风险度量表示的结果，并且得到了Lp-空间上的表示定理的一种新的证明方法.它们分别是文献［2］的相关结论从L∞-空间到Lp-空间上的推广和对Inoue［4］做的一些补充证明.

Lp-空间；连续一致风险度量；在险值

MR（2010）主题分类号：62P05；91B30O211.9

date：2015-03-30Accepted date：2015-05-06

Supported by National Natural Science Foundation of China（11371284）.

Biography：Chen Yanhong（1988-），female，born at Shaoyang，Hunan，master，major in financial mathematics.