A NOTE ON CYCLIC CODES OVER Fpm+uFpm+u2Fpm

LIU Xiu-sheng

(School of Mathematics and Physics，Hubei Polytechnic University，Huangshi 435003，China）

A NOTE ON CYCLIC CODES OVER Fpm+uFpm+u2Fpm

LIU Xiu-sheng

(School of Mathematics and Physics，Hubei Polytechnic University，Huangshi 435003，China）

In this paper，we study cyclic codes of length psover the ring Fpm+uFpm+u2Fpm. By establishing the homomorphism from ring Fpm+uFpm+u2Fpmto ring Fpm+uFpm，we give the new classify method for cyclic codes of length psover the ring Fpm+uFpm+u2Fpm.Using the method of the classify，we obtain the number of codewords in each of cyclic codes of length psover ring Fpm+uFpm+u2Fpm.

local ring；cyclic codes；repeated-root codes；the number of codewords

2010 MR Subject Classification：94B05；94B15

Document code：AArticle ID：0255-7797（2016）05-0981-06

1 Introduction

Let Fpmbe a finite field with pmelements，where p is a prime and m is an integer number. Let R be the commutative ring Fpm+uFpm+u2Fpm=｛a+bu+cu2|a，b，c∈Fpm｝with u3=0.The ring R is a chain ring，which has a unique maximal ideal〈u〉=｛au|a∈Fpm｝（see［3］）.A code of length n over R is a nonempty subset of Rn，and a code is linear over R if it is an R-submodule of Rn.Let C be a code of length n over R and P（C）be its polynomial representation，i.e.，

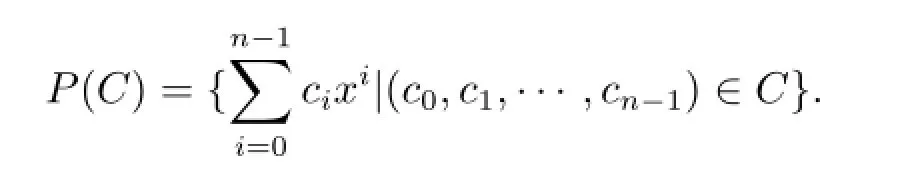
The notions of cyclic shift and cyclic codes are standard for codes over R.Briefly，for the ring R，a cyclic shift on Rnis a permutation T such that

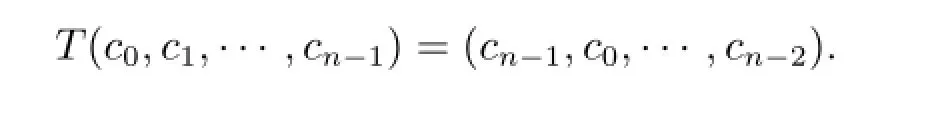
A linear code over ring R of length n is cyclic if it is invariant under cyclic shift.It is known that a linear code over ring R is cyclic if and only if P（C）is an ideal of［5］）.

The following two theorems can be found in［1］.

Theorem 1.1

Type 1〈0〉，〈1〉.

Type 2 I=〈u（x-1）i〉，where 0≤i≤ps-1.

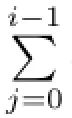
Type 4 I=〈（x-1）i+（x-1）j，u（x-1）w〉，where 1≤i≤ps-1，c1j∈Fpm，w＜l and w＜T，where T is the smallest integer such that u（x-1）T∈〈（x-1）i+（x-1）j〉；or equivalently，〈（x-1）i+u（x-1）th（x），u（x-1）w〉，with h（x）as in Type 3，and deg（h）≤w-t-1.

Theorem 1.2 Let C be a cyclic code of length psover Fpm+uFpm，as classified in Theorem 1.1.Then the number of codewords nCof C is determined as follows.

If C=〈0〉，then nC=1.

If C=〈1〉，then nC=p2mps.

If C=〈u（x-1）i〉，where 0≤i≤ps-1，then nC=pm（ps-i）.

If C=〈（x-1）i〉，where 1≤i≤ps-1，then nC=p2m（ps-i）.

If C=〈（x-1）i+u（x-1）th（x）〉，where 1≤i≤ps-1，0≤t＜i，and h（x）is a unit，then

If C=〈（x-1）i+u（x-1）th（x），u（x-1）κ〉，where 1≤i≤ps-1，0≤t＜i，either h（x）is 0 or h（x）is a unit，and

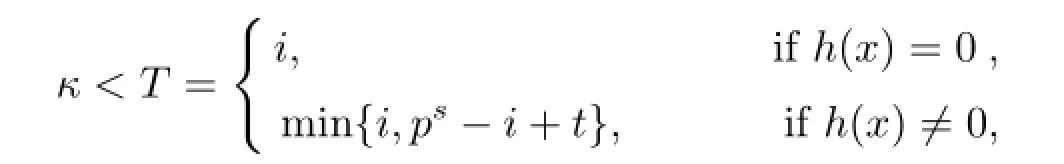
then nC=pm（2ps-i-κ）.

Recently，Liu and Xu［3］studied constacyclic codes of length psover R.In particular，they classified all cyclic codes of length psover R.But they did not give the number of codewords in each of cyclic codes of length psover R.In this note，we study repeatedroot cyclic codes over R by using the different method from［2］，and obtain the number of codewords in each of cyclic codes of length psover R.

2 Cyclic Codes of Length psover R

Cyclic codes of length psover R are ideals of the residue ring R1= to prove the ring R1is a local ring with the maximal ideal〈u，x-1〉，but it is not a chain ring.

We can list all cyclic codes of length psover R1as follows.

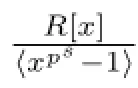
Type 1〈0〉，〈1〉.

Type 2I=〈u2（x-1）k〉，where 0≤k≤ps-1.

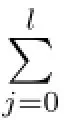
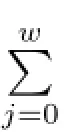
Type 5I=〈（x-1）i+u（x-1）th1（x）+u2（x-1）zh2（x）〉，where 1≤i≤ps-1，0≤t＜i，0≤z＜i and h1（x），h2（x）are similar to h（x）in Type 3.

Type 6I=〈（x-1）i+u（x-1）th1（x）+u2（x-1）zh2（x），u2（x-1）η〉，where 1≤i≤ps-1，0≤t＜i，0≤z＜i，h1（x），h2（x）are similar to h（x）in Type 3，η＜i，and η is the smallest integer such that u2（x-1）η∈〈（x-1）i+u（x-1）th1（x）+u2（x-1）zh2（x）〉.

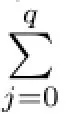
Type 8I=〈（x-1）i+u（x-1）th1（x）+u2（x-1）zh2（x），u（x-1）q+u2e2j（x-1）j，u2（x-1）σ〉，where 1≤i≤ps-1，σ＜q≤i，0≤t≤i，0≤z≤i，q＜T≤i，T is the smallest integer such that u（x-1）T∈〈（x-1）i+u（x-1）th1（x）〉，and σ is the smallest integer such that u2（x-1）σ∈〈u（x-1）q+u2e2j（x-1）j〉，and h1（x），h2（x）are similar to h（x）in Type 3.

Proof Ideals of Type 1 are the trivial ideals.Consider an arbitrary nontrivial ideal of R1.

Start with the homomorphism φ：Fpm+uFpm+u2Fpm→Fpm+uFpmwith φ（a+ub+ u2c）=a+ub.This homomorphism then can be extended to a homomorphism of rings of polynomials

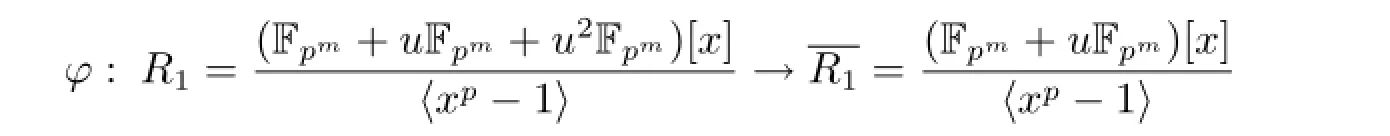
by letting φ（c0+c1x+···+cps-1xps-1）=φ（c0）+φ（c1）x+···+φ（cps-1）xps-1.Note that Kerφ=.

Now，let us assume that I is a nontrivial ideal of R1.Then φ（I）is an ideal of.But ideals ofare characterized.So we can make use of these results.

On the other hand，Kerφ is also an ideal of.We can consider it to be u2times a ideal of.This means that we can again use the results in the aforementionedpapers.By using the characterization in［2］，we have

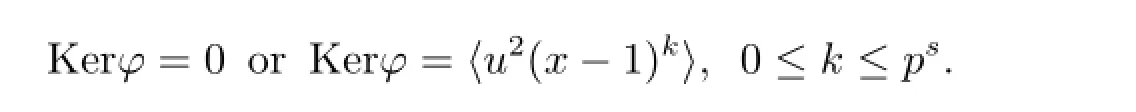
For φ（I），by using the characterization in［1］，we shall discuss φ（I）by carrying out the following cases.

Case 1 φ（I）=0.Then I=〈u2（x-1）k〉，where 0≤k≤ps-1.

Case 2 φ（I）/=0.We now have seven subcases.

Case 2a φ（I）=〈u（x-1）l〉，where 0≤l≤ps-1.

If Kerφ/=0，then Kerφ=〈u2（x-1）w〉，where 0≤w≤ps-1.Hence

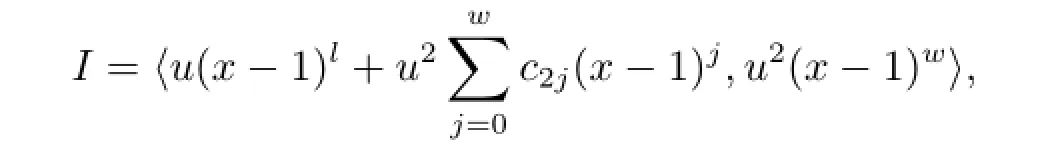
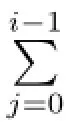
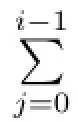
If Kerφ/=0，then

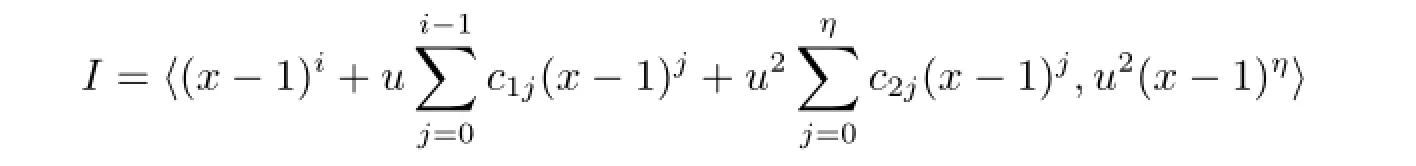
or

where 1≤i≤ps-1，c1j，c2j∈Fpm，η＜i，η is the smallest integer such that u2（x-1）η∈〈（x-1）i+u（x-1）th1（x）+u2（x-1）zh2（x）〉，and h1（x），h2（x）are similar to h（x）in Type 3.

Case 2c φ（I）=〈（x-1）i+u（x-1）th1（x），u（x-1）q〉，where 1≤i≤ps-1，0≤t≤i，q＜T，and T is the smallest integer such that u（x-1）T∈〈（x-1）i+u（x-1）th1（x）〉，h1（x）is similar to h（x）in Type 3.

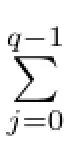
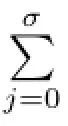
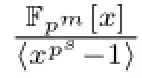
Theorem 2.2 Let C be a cyclic code of length psover R，as classified in Theorem 2.1. Then the number of codewords nCof C is determined as follows.

If C=〈0〉，then nC=1.

If C=〈1〉，then nC=p3mps.

If C=〈u2（x-1）k〉，where 0≤k≤ps-1，then nC=pm（ps-k）.

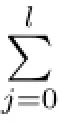
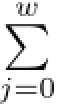
If C=〈（x-1）i〉，where 1≤i≤ps-1，then nC=p2m（ps-i）.

If C=〈（x-1）i+u（x-1）th1（x）+u2（x-1）zh2（x）〉，where 1≤i≤ps-1，0≤t＜i，0≤z＜i and h1（x）is a unit，then

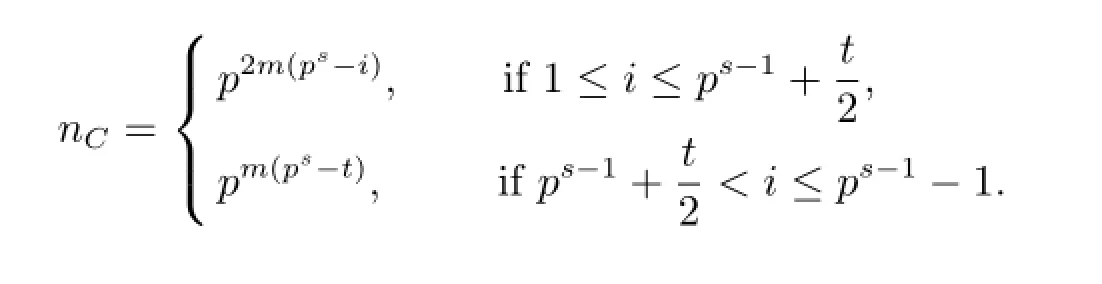
If C=〈（x-1）i+u（x-1）th1（x）+u2（x-1）zh2（x），u2（x-1）η〉，where 1≤i≤ps-1，0≤t＜i，0≤z＜i，h1（x）is a unit，η＜i，η is the smallest integer such that u2（x-1）η∈〈（x-1）i+u（x-1）th1（x）+u2（x-1）zh2（x）〉，and h1（x）is a unit，then

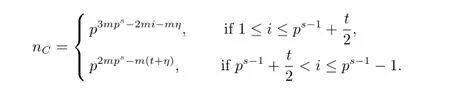
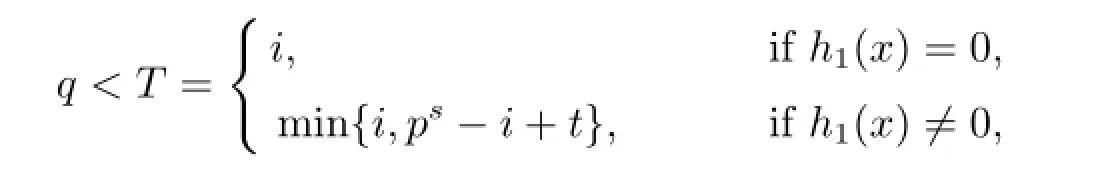
then nC=pm（2ps-i-q）.

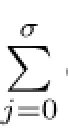
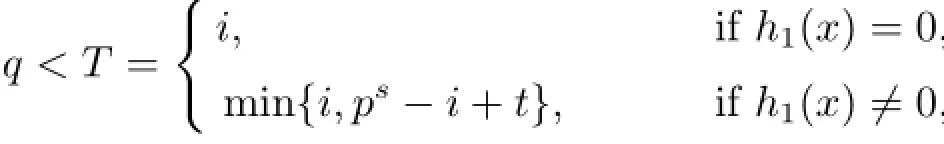
then nC=p3mps-m（i+q+σ）.

References

［1］Dinh H Q.Constacyclic codes of length psover Fpm+uFpm［J］.J.Alg.，2010，324：940-950.

［2］Dinh H Q.On the linear ordering of some classes of negacyclic and cyclic codes and their distance distributions［J］.Finite Field Appl.，2008，14：22-40.

［3］Liu X S，Xu X.Some classes of repeated-root constacyclic codes over Fpm+uFpm+u2Fpm［J］.J. Korean Math.Soc.，2014，51（4）：853-866.

［5］Hammous A，Kumar P V，Calderbark A R，Sloame J A，Sol´e P.The Z4-linearity of Kordock，Preparata，Goethals，and releted codes［J］.IEEE Trans.Inform.The.，1994，40：301-319.

［5］Huffman W C，Pless V.Fundamentals of error-correcting codes［M］.Cambridge：Cambridge Univ. Press，2003.

关于环Fpm+uFpm+u2Fpm上循环码的注记

刘修生
（湖北理工学院数理学院，湖北黄石435003）

本文研究了环Fpm+uFpm+u2Fpm上长度为ps的循环码分类.通过建立环Fpm+uFpm+ u2Fpm到环Fpm+uFpm的同态，给出了环Fpm+uFpm+u2Fpm上长度为ps的循环码的新分类方法.应用这种方法，得到了环Fpm+uFpm+u2Fpm长度为ps的循环码的码词数.

局部环；循环码；重根循环码；码词数

MR（2010）主题分类号：94B05；94B15O157.4

date：2015-11-16Accepted date：2016-03-04

Supported by Scientific Research Foundation of Hubei Provincial Education Department of China（D20144401；B2015096）and the National Science Foundation of Hubei Polytechnic University of China（12xjz14A）.

Biography：Liu Xiusheng（1960-），male，born at Daye，Hubei，professor，major in groups and algebraic coding，multiple linear algebra.