NUMERICAL STABILITY ANALYSIS FOR EQUATION x＇）t）=ax）t）+bx）3［）t+1）/3］）

WANG Qi，WANG Xiao-ming，CHEN Xue-song

(School of Applied Mathematics，Guangdong University of Technology，Guangzhou 510006，China）

NUMERICAL STABILITY ANALYSIS FOR EQUATION x＇）t）=ax）t）+bx）3［）t+1）/3］）

WANG Qi，WANG Xiao-ming，CHEN Xue-song

(School of Applied Mathematics，Guangdong University of Technology，Guangzhou 510006，China）

2010 MR Subject Classification：65L07；65L20

Document code：AArticle ID：0255-7797（2016）05-0955-08

1 Introduction

We are interested in the numerical stability of the Euler-Maclaurin method for the following differential equation with piecewise constant arguments（EPCA）：

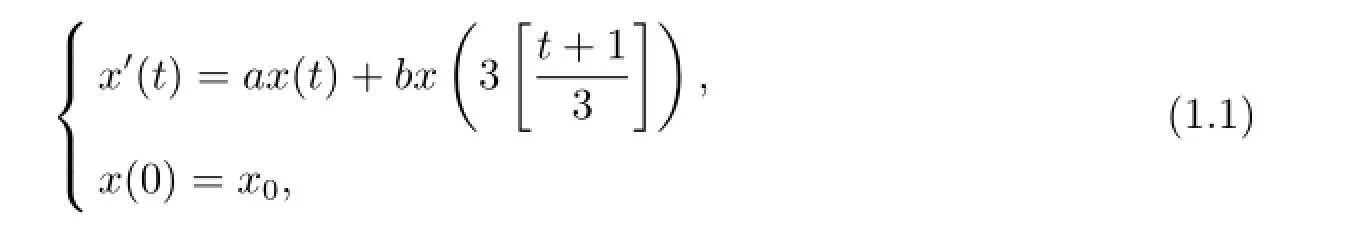
where t＞0，a/=0，b and x0are real constants and［·］denotes the greatest integer function.

EPCA belongs to one special kind of delay differential equations［1-3］.They described hybrid dynamical systems and combine properties of both differential and difference equations.So EPCA had many applications in science and engineering.In the past twenty years，many researchers investigated the properties of the exact solution of EPCA（see［4-6］and the references therein）.In particularly，stability of solutions of EPCA received much attention（see［7-9］and the extensive bibliography therein）.For more information on this type of equations，the interested readers can refer Wiener's book［10］.Recently，special interest was shown to the properties of numerical solution of EPCA，such as stability［11，12］，dissipativity［13］and oscillation［14］.In this paper，we will study the stability of the numericalsolution in the Euler-Maclaurin method for（1.1）.Whether the numerical method preserves stability of the exact solution is considered.Two numerical examples for demonstrating the theoretical results are also provided.

The following results give the definition and stability of exact solution for（1.1）.

Definition 1.1（see［10］）A solution of（1.1）on［0，∞）is a function x（t）which satisfies the conditions

（i）x（t）is continuous on［0，∞）；

（ii）the derivative x＇（t）exists at each point t∈［0，∞），with the possible exception of the points t=3n-1 for n∈N，where one-sided derivatives exist；

（iii）（1.1）is satisfied on each interval［3n-1，3n+2）for n∈N.

Theorem 1.2（see［10］）Assume that a，b and x0∈R，then（1.1）has on［0，∞）a unique solution x（t）given by

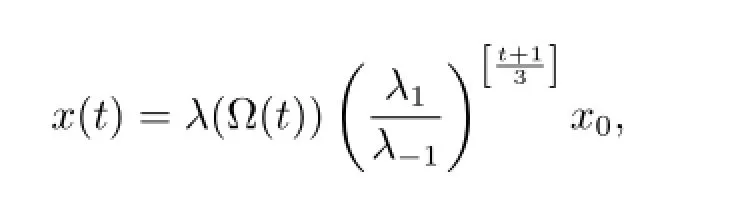
where

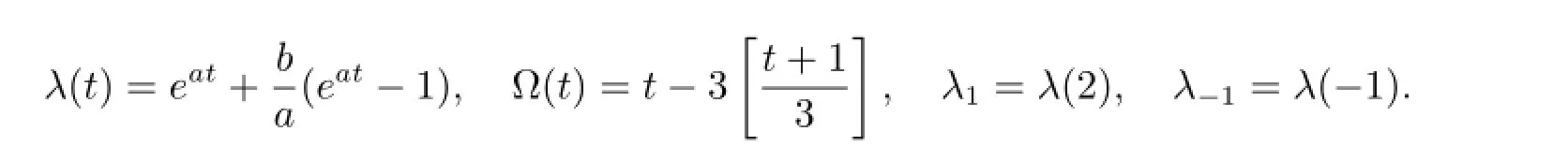
Theorem 1.3（see［10］）The solution x（t）=0 of（1.1）is asymptotically stable（x（t）→0 as t→∞）if and only if any one of the following conditions is satisfied

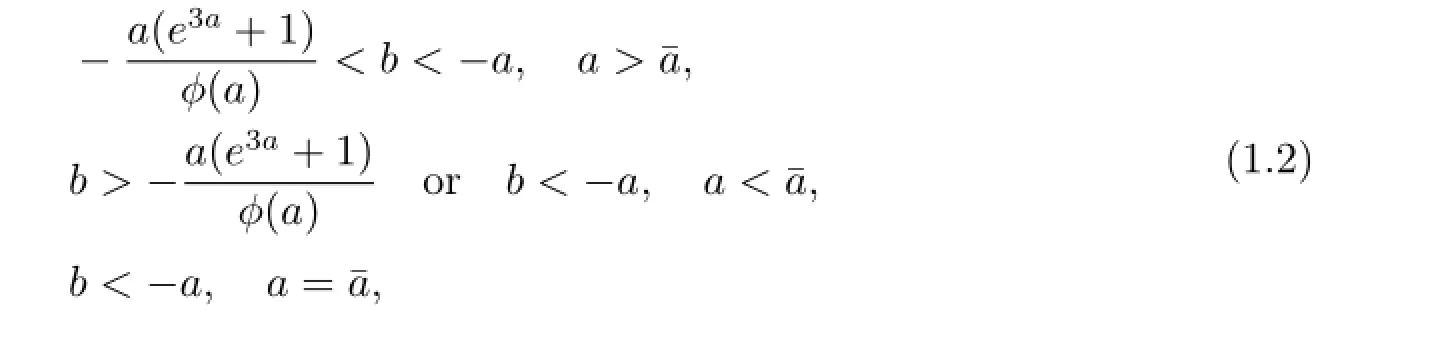
where¯a is the nonzero solution of equation φ（x）=e3x-2ex+1=0.

2 Stability of Numerical Solution

2.1 The Euler-Maclaurin Method

Let h be a given stepsize，m≥1 be a given integer and satisfies h=1/m.The gridpoints tibe defined by ti=ih（i=0，1，2，···）.Applying the Euler-Maclaurin formula to（1.1），we have

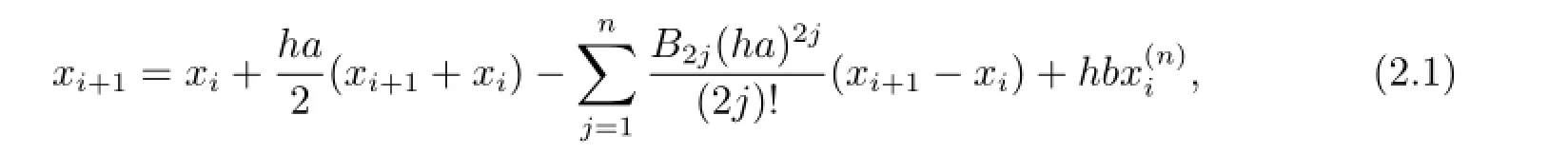
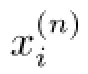
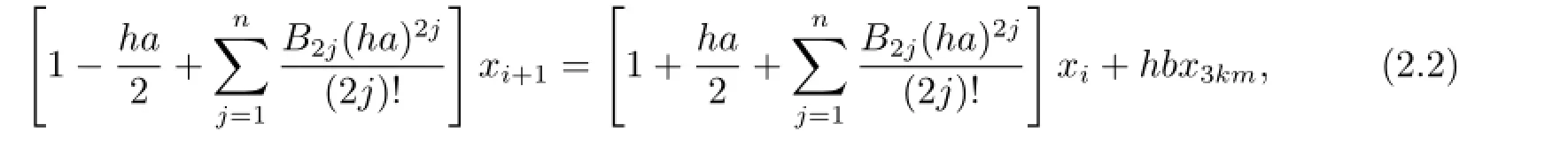
which is equivalent to

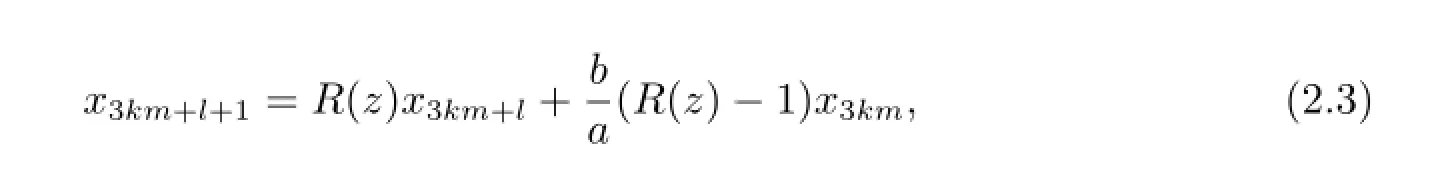
where

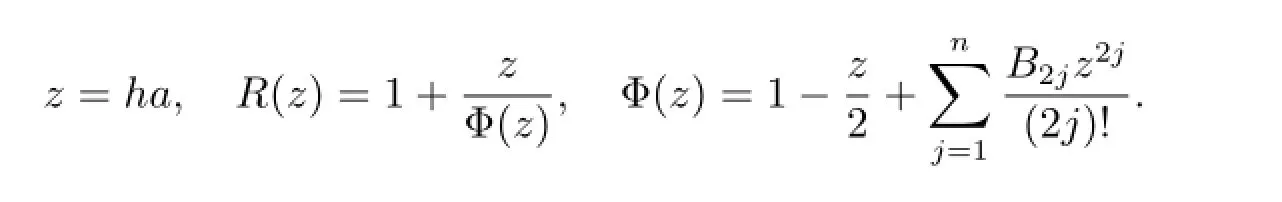
Thus

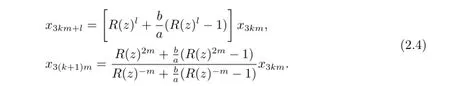
Similar to Theorem 2.2 in［14］，we have the following result for convergence.

Theorem 2.1For any given n∈N，the Euler-Maclaurin method is of order 2n+2. 2.2 Stability Analysis

Definition 2.2 The Euler-Maclaurin method is called asymptotically stable at（a，b）if there exists a constant M0such that xndefined by（2.3）tends to zero as n→∞for all h=1/m and any given x0.

Lemma 2.3（see［15］）If|z|＜1，then Φ（z）≥1/2 for z＞0 and Φ（z）≥1 for z＜0.

Lemma 2.4（see［15］）If|z|＜1，then

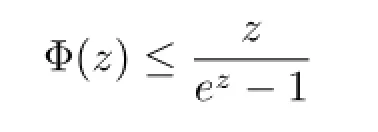
for n is even and

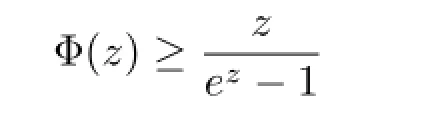
for n is odd.

Theorem 2.5The Euler-Maclaurin method is asymptotically stable if any one of the following conditions is satisfied

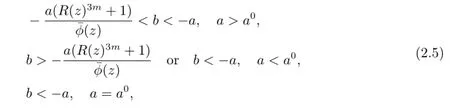
ProofLet

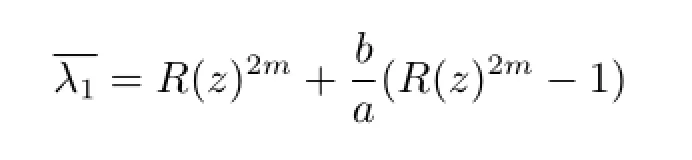
and

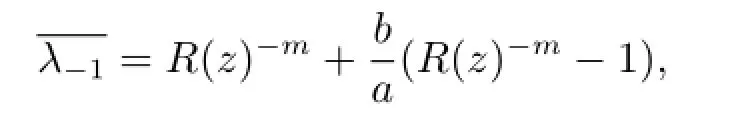
so we need to verify

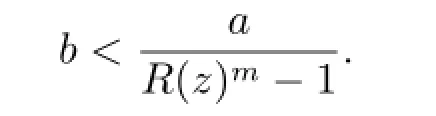
Then（2.6）is equivalent to

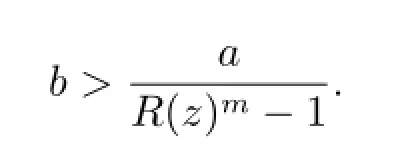
Then（2.6）is equivalent to

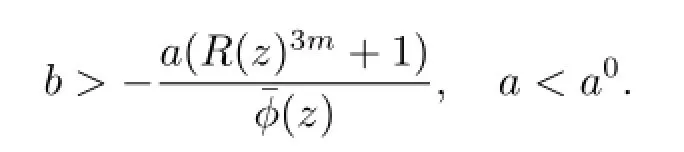
The proof is completed.

The following two lemmas are given naturally.

Lemma 2.6 Let f（r）=r3-2r+1，r＞0，then

（a）the function f（r）has a minimum at r1=，and f（r）is decreasing in［0，r1） and increasing in［r1，+∞）；

（b）the function f（r）has a unique solution 1＞r0/=1；

（c）f（r）＜0 if r∈［r0，1）and f（r）＞0 if r∈［0，r0）or r∈［1，+∞）.

Lemma 2.7 Let

then

（a）the function g（ω）has extremum at ω1=

（b）g（ω）is increasing in（0，r0）and（r0，ω1）；

（c）g（ω）is decreasing in（ω1，1）and（1，+∞）.

By Lemmas 2.6 and 2.7，we obtain

Corollary 2.8 Assume that r0/=1 is a unique solution of the function f（r）=r3-2r+1，then r0＜ω1＜r1＜1.

So we have the following result.

Theorem 2.9Assume that（1.1）is asymptotically stable，then the Euler-Maclaurin method is asymptotically stable if one of the following conditions is satisfied

（a）R（z）m≤ea（a≤lnω1）；

（b）R（z）m≥ea（lnω1＜a＜0）；

（c）R（z）m≤ea（a≥0）.

ProofIn view of Theorems 1.2 and 2.5，we will prove that condition（2.5）is satisfied under condition（1.2）.

If（a）holds，then we know from Lemmas 2.3 and 2.4 that f（r）is decreasing and g（ω）is increasing.Hence¯a＜a0and

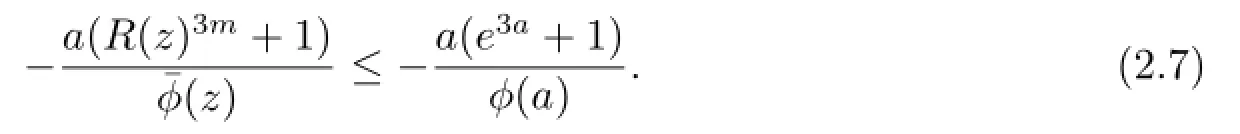
From Lemmas 2.3，2.4 and Theorem 2.9，we have the following main result in this paper.

Theorem 2.10The Euler-Maclaurin method preserves the stability of（1.1）if one of the following conditions is satisfied

（a）n is odd if ea＞ω1，

（b）n is even if ea≤ω1.

3 Numerical Experiments

Consider the following two problems

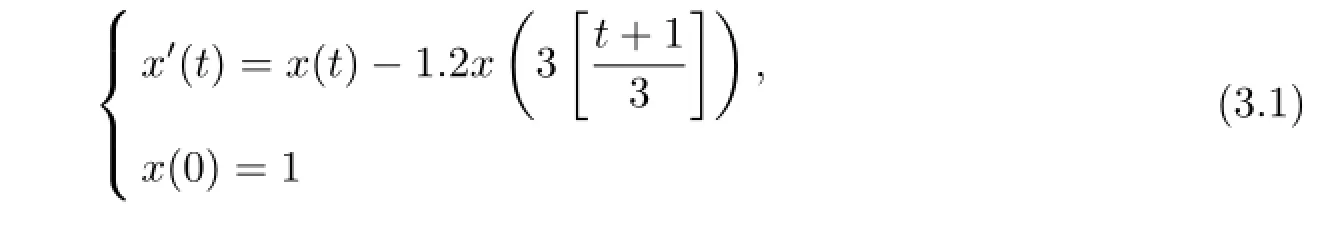
and

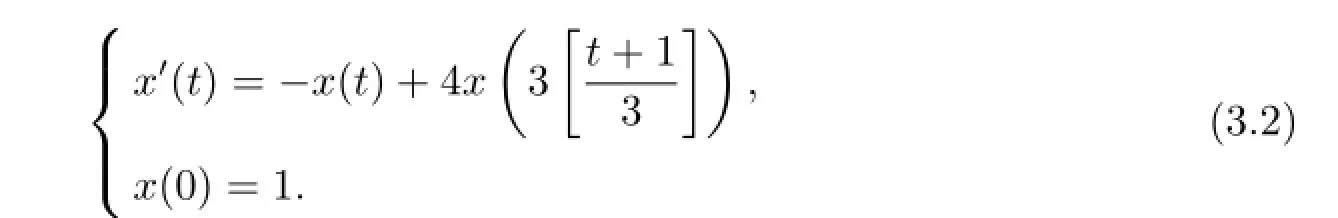
In Figures 1 and 2，we plot the exact solution and the numerical solution for（3.1），respectively.Moreover，for（3.2），we also plot the exact solution and the numerical solution in Figures 3 and 4，respectively.We can see from these figures that the Euler-Maclaurin method preserves the stability of（3.1）and（3.2），which is coincide with Theorem 2.10.

AcknowledgementsThe authors would like to thank the anonymous reviewers for their careful reading.Many thanks to Professors Mingzhu Liu，Minghui Song and Zhanwen Yang for their great help and valuable suggestions.

Figure 1：the exact solution of（3.1）

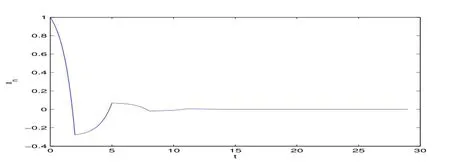
Figure 2：the numerical solution of（3.1）with n=3 and m=50

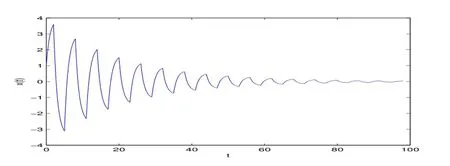
Figure 3：the exact solution of（3.2）

Figure 4：the numerical solution of（3.2）with n=2 and m=40

References

［1］Cheng Shengmin，Zhou Shaobo.Convergence and stability of numerical methods for stochastic differential delay equation［J］.J.Math.，2014，34（6）：1073-1084.

［2］Wang Xiao，Cui Cheng，Xiao Li，et al.Existence and uniqueness of solutions for differential equations with time delay and impulsive differential equations with time delay［J］.J.Math.，2013，33（4）：683-688.

［3］Ashyralyev A，Agirseven D.On convergence of difference schemes for delay parabolic equations［J］. Comput.Math.Appl.，2013，66（7）：1232-1244.

［4］Cooke K L，Wiener J.Retarded differential equations with piecewise constant delays［J］.J.Math. Anal.Appl.，1984，99（1）：265-297.

［5］Wiener J，Aftabizadeh A R.Differential equations alternately of retarded and advanced type［J］.J. Math.Anal.Appl.，1988，129（1）：243-255.

［6］Liang Haihua，Wang Genqiang.Oscillation criteria of certain third-order differential equation with piecewise constant argument［J］.J.Appl.Math.，2012，2012：1-18.

［7］Alwan M S，Liu Xinzhi，Xie Weichau.Comparison principle and stability of differential equations with piecewise constant arguments［J］.J.Franklin I.，2013，350（2）：211-230.

［8］Akhmet M U.Stability of differential equations with piecewise constant arguments of generalized type［J］.Nonl.Anal.，2008，68（4）：794-803.

［9］Li Huaixing，Muroya Y，Nakata Y，et al.Global stability of nonautonomous logistic equations with a piecewise constant delay［J］.Nonl.Anal.，RWA，2010，11（3）：2115-2126.

［10］Wiener J.Generalized solutions of functional differential equations［M］.Singapore：World Scientific，1993.

［11］Song Minghui，Yang Zhanwen，Liu Mingzhu.Stability of θ-methods for advanced differential equations with piecewise continuous arguments［J］.Comput.Math.Appl.，2005，49（9-10）：1295-1301.

［12］Liang Hui，Liu Mingzhu，Yang Zhanwen.Stability analysis of Runge-Kutta methods for systems u＇（t）=Lu（t）+Mu（［t］）［J］.Appl.Math.Comput.，2014，228（1）：463-476.

［13］Wang Wansheng，Li Shoufu.Dissipativity of Runge-Kutta methods for neutral delay differential equations with piecewise constant delay［J］.Appl.Math.Lett.，2008，21（9）：983-991.

［14］Liu Mingzhu，Gao Jianfang，Yang Zhanwen.Preservation of oscillations of the Runge-Kutta method for equation x＇（t）+ax（［t］）+a1x（［t-1］）=0［J］.Comput.Math.Appl.，2009，58（6）：1113-1125.

［15］L¨u Wanjin，Yang Zhanwen，Liu Mingzhu.Stability of the Euler-Maclaurin methods for neutral differential equations with piecewise continuous arguments［J］.Appl.Math.Comput.，2007，186（2）：1480-1487.

In this paper，we investigate the numerical stability of Euler-Maclaurin method for differential equation with piecewise constant arguments x＇（t）=ax（t）+bx（3［（t+1）/3］）.By the method of characteristic analysis，the sufficient conditions of stability for the numerical solution are obtained.Moreover，we show that the Euler-Maclaurin method preserves the stability of the exact solution.Finally，some numerical examples are given.

Euler-Maclaurin method；piecewise constant arguments；stability；numerical solution

方程x＇）t）=ax）t）+bx）3［）t+1）/3］）的数值稳定性分析

王琦，汪小明，陈学松
（广东工业大学应用数学学院，广东广州510006）

date：2014-08-30Accepted date：2015-03-16

Supported by National Natural Science Foundation of China（11201084）；China Postdoctoral Science Foundation（2013M531842）and Science and Technology Program of Guangzhou （2014KP000039）.

本文研究了分段连续型微分方程x＇（t）=ax（t）+bx（3［（t+1）/3］）Euler-Maclaurin方法的数值稳定性问题.利用特征分析的方法，获得了数值解稳定的充分条件，进而证明了Euler-Maclaurin方法保持了精确解的稳定性.最后给出了一些数值例子.

Euler-Maclaurin方法；分段连续项；稳定性；数值解

MR（2010）主题分类号：65L07；65L20O241.81

Biography：Wang Qi（1978-），male，born at Yichun，Heilongjiang，associate professor，major in numerical computation of differential equation.