联合时频分布和压缩感知对抗频谱弥散干扰

卢云龙 李 明 曹润清 王泽玉 陈洪猛



联合时频分布和压缩感知对抗频谱弥散干扰

卢云龙*李 明 曹润清 王泽玉 陈洪猛

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)

频谱弥散(SMSP)干扰是一种专门对抗线性调频脉冲雷达的有源欺骗干扰。针对SMSP干扰的抑制问题，该文根据该干扰的时频分布特性，提出一种联合时频分布和压缩感知的干扰抑制算法。该方法通过在时频域丢弃SMSP干扰信号，保留属于目标信号的时频点，并根据保留的时频点与雷达回波频谱间的线性关系，建立压缩感知最小问题求解模型并利用正交匹配追踪方法重构目标信号，实现对SMSP干扰的抑制。Monte Carlo仿真结果验证了该方法的有效性。

有源欺骗干扰；干扰抑制；时频分析；压缩感知

1 引言

有源欺骗干扰严重降低雷达对目标的检测性能。而基于数字射频存储(Digital Radio Frequency Memory, DRFM)技术的频谱弥散(SMeared SPectrum, SMSP)干扰是一种专门对抗线性调频(Linear Frequency Modulated, LFM)脉冲雷达的有源欺骗干扰方式[1]。干扰机对截获的雷达信号进行采样和存储，并通过特定的调制规律调制产生SMSP干扰信号并转发给目标雷达。雷达接收机对SMSP干扰信号的匹配滤波处理，导致在雷达输出端产生距离多瓣输出结构，即在真实目标附近形成大量的假目标，使得雷达难以正确检测到真实目标。

DRFM有源欺骗干扰因其与雷达发射信号高度相似而难以检测和抑制。有学者分别从干扰机本身量化数字特性[2,3]、雷达发射波形[4]、空时自适应处理以及2维图像域[8]等角度出发提出相应的对抗有源欺骗干扰算法并取得一定成效。而针对SMSP干扰的检测和抑制问题，文献[9]在组网雷达系统框架下提出了基于分数阶功率谱的干扰检测算法；文献[10]提出一种基于匹配信号变换的SMSP干扰识别算法；这两种方法都是利用SMSP干扰信号频率调制特性差异实现对干扰的检测及识别，但并没有给出干扰的抑制方法。文献[11]提出了一种基于分数阶傅里叶变换(FRactional Fourier Transform, FRFT)域扫频滤波的SMSP干扰抑制方法，但该方法无法滤除滤波器带宽内的干扰信号，同时对滤波器带宽的要求比较高。当滤波器带宽过小，会导致部分目标信号的损失，使得重构的目标信号严重失真。当滤波器带宽过大，较大的干扰信号能量进入滤波器，导致脉冲压缩后在真实目标附近产生少数假目标旁瓣，影响雷达获取真实目标信息。

在时频域，SMSP干扰信号与目标信号是耦合的，即部分时频支撑区是重叠的，因此直接在时频域进行遮盖滤波会导致目标信号的损失[12]。为此本文引入压缩感知概念，提出一种联合时频分布和压缩感知的抗干扰策略。该方法先通过FRFT在u域预滤除与目标信号不重叠的SMSP干扰信号分量，并对滤波后信号进行解调频处理以保证解调后的信号在频域是稀疏的(线性调频信号经解调频后变为单频信号)。然后在短时傅里叶变换(Short Time Fourier Transform, STFT)域根据L-estimate准则，通过遮盖SMSP干扰与目标信号重叠的时频支撑区实现对残余SMSP干扰信号的滤除。显然该操作在滤除残余SMSP干扰信号的同时也会导致部分目标信号的丢失。为了能精确重构目标信号，根据遮盖滤波后的STFT分布与信号的稀疏频域之间的线性关系，建立压缩感知最小问题求解模型并重构目标信号，实现对SMSP干扰的抑制。相比文献[11]的FRFT干扰抑制方法，本文方法在完全抑制SMSP干扰的同时能有效保留目标信号信息，即重构的目标信号不会产生相位失真。

2 干扰信号特性分析

令PD雷达发射基带线性调频信号，如式(1)所示。

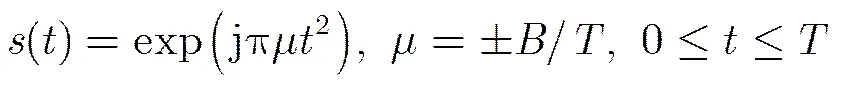
根据SMSP干扰产生的原理[1]，该类型干扰由“”个相同子脉冲复合而成。子脉冲也为线性调频信号，与雷达发射信号有相同的带宽，脉宽变为发射信号的，因此其调频率是雷达发射信号调频率的倍。第个子脉冲可表示为

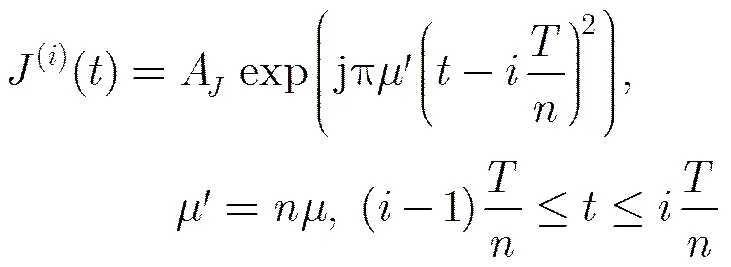
进而可得到SMSP的表达式：

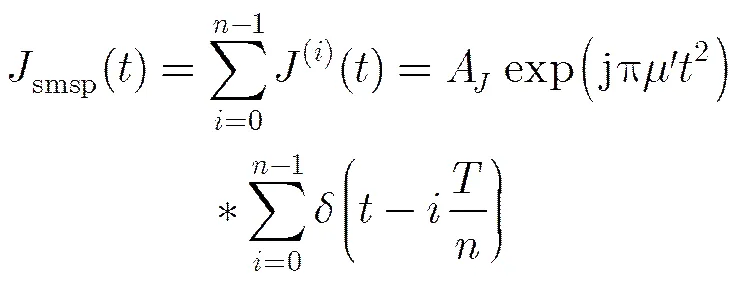
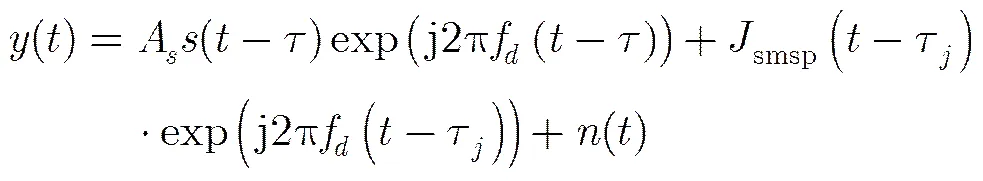
3 联合时频分布和压缩感知的抗干扰方法

由第2小节分析可知，SMSP干扰与目标信号不论在时域或频域上都存在耦合，因此即使假设先验知道目标信号的频率信息，也无法利用理想的陷波器提取目标信号。同理在分数阶傅里叶变换域，也无法找到一个合适的旋转角度完全分离目标信号与干扰[11]。而在时频域，目标信号与SMSP干扰只在少数时频支撑区重叠，通过遮盖属于SMSP干扰信号的时频点(包括干扰信号与目标信号重叠的时频点)，即可有效抑制SMSP干扰信号。但是可以看出，时频域遮盖滤波在滤除SMSP干扰信号的同时也丢弃了部分目标信号信息，如果直接利用时频综合等方法重构目标信号[16]，将会导致重构的目标信号产生失真。因此，本文引入压缩感知概念，从较少的数据中重构出完整的目标信号，实现对SMSP干扰的有效抑制。

图1 回波时域波形        图2 回波频谱        图3 回波STFT时频分布

3.1 分数阶傅里叶变换域预处理

SMSP干扰与目标信号在频域耦合并且是非稀疏的，为联合压缩感知方法重构目标信号，需要保证雷达回波在频域上是稀疏的。由SMSP干扰产生的原理可知其调频率与雷达发射信号的调频率是不匹配的[1]，因此以雷达发射信号为参考信号直接对雷达回波解调频，并不能保证解调后的信号在频域是稀疏的。而在FRFT域，通过设计合适的扫频滤波器滤除与目标信号不重叠的SMSP干扰信号分量，并对滤波后的信号进行解调频操作，由于解调频后的信号近似为单频信号，因此其在频域是稀疏的[14]。

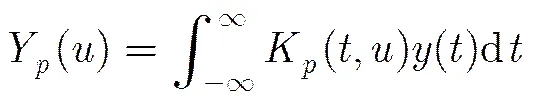
其中，

(6)

信号在FRFT域的信息可由2维峰值搜索来获取，由于雷达发射信号信息相对于雷达方来说是已知的，因此可以通过理论计算旋转角度，实现信号的阶FRFT。其中,为雷达发射信号的调频率。考虑到当JSR较大时，通过峰值搜索的方法可能导致中心频率估计错误，同时为了减少计算量，这里我们利用雷达发射信号先验已知的优势，理论估计滤波器中心频率，并设置较大的滤波器带宽以减少目标信号分量的损失[11,17]。设置较大的滤波器带宽会导致更多的SMSP干扰能量进入滤波器，由于在时频域可以通过遮盖滤波滤除干扰分量，因此这并不影响本文方法的SMSP干扰抑制性能。

雷达回波经FRFT域扫频滤波后，大部分SMSP干扰被抑制，仅目标信号及与目标信号重叠的SMSP干扰分量通过滤波器。用雷达发射信号为参考信号对扫频滤波后的雷达回波进行解调频操作，使得解调频后的信号在频域是稀疏的[14]。

3.2 非重叠窗短时傅里叶变换时频表示

短时傅里叶变换是一种线性变换，在处理多分量信号时可以避免交叉项的出现，并且各自分量信号对应的时频点能量是相等的。为了有效建立信号的时频分布与频域之间的线性关系，同时避免时频信息冗余，本文采用非重叠窗短时傅里叶变换，即所有滑窗内的信号是不重叠的。

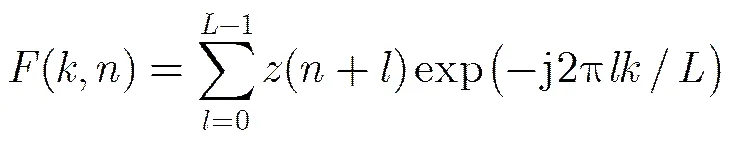
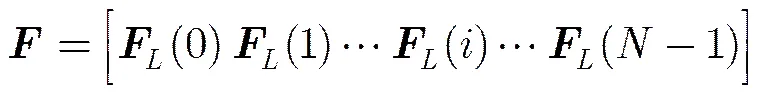
(9)

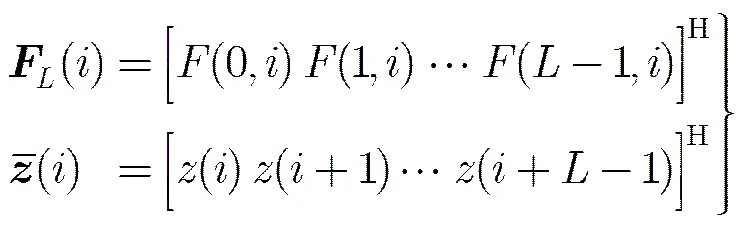
(11)

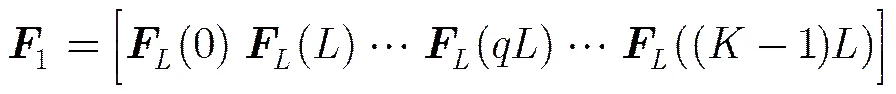
(13)

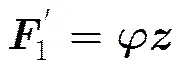
(15)

3.3 基于压缩感知的目标信号重构

L-estimate是Huber估计理论中的一种顺序统计量，其在信号和图像滤波及信号降噪中得到广泛应用[18,19]。在时频域，短时傅里叶变换作为一种线性变换，单分量目标信号的时频点能量是相等的。而SMSP干扰信号与目标信号的交叉重叠，导致重叠部分的时频点能量，可能因干扰信号与目标信号相位相同而增大，也可能因相位相反而减小。利用目标信号未与SMSP干扰信号重叠的时频点能量和与SMSP干扰信号重叠的时频点能量的差异，根据L-estimate准则，丢弃目标信号与SMSP干扰信号重叠的时频点，并根据保留的时频点与信号稀疏频域之间的线性关系建立压缩感知最小问题求解模型，进而利用压缩感知重构算法恢复目标信号。

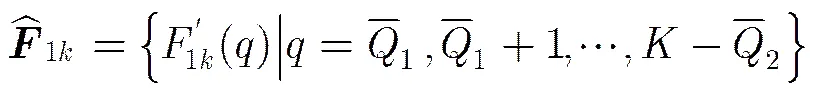
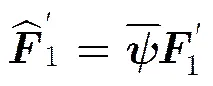
(18)

4 实验结果与分析

SMSP多用于突防环境下的自卫式密集假目标干扰。令脉冲雷达发射脉宽为，带宽为20 MHz的线性调频信号，采样频率为51.2 MHz。定义干信比(Jamming-to-Signal Ratio, JSR)，信噪比(Signal-to-Noise Ratio, SNR)，其中为目标信号，为SMSP干扰信号，为服从分布的零均值复高斯白噪声。仿真中设置SMSP干扰子脉冲数，信噪比设定为10 dB，干信比变化范围为：3~15 dB，变化间隔为1 dB。信号的不连续非重叠短时傅里叶变换的滑窗为窗长的矩形窗。时频域时频点筛选条件设为和。

图4 抗SMSP干扰算法流程图

图5给出了雷达被施加SMSP干扰时的雷达回波脉冲压缩结果，其中为15 dB。从图5中可以看出，当雷达回波中包含SMSP干扰时，雷达接收机匹配滤波器输出端会产生一列梳齿状波瓣，形成大量假目标，而目标回波的输出波瓣淹没在其中，使得雷达失去对目标信息的获取能力。FRFT扫频滤波方法在u域通过扫频滤波器保留滤波器带宽内的信号分量从而实现SMSP干扰的抑制。图6给出了经FRFT扫频滤波方法干扰抑制后信号的时频分布，对比图3可以发现，雷达回波经u域FRFT扫频滤波后，与目标信号不重叠的干扰分量被滤除，而与目标信号重叠的干扰分量会随目标信号一起通过滤波器，因此FRFT方法无法完全滤除干扰信号。

图7给出了丢弃SMSP干扰信号与目标信号重叠的时频点后保留下来的时频点信息。可以看出，在丢弃干扰信号与目标信号重叠时频点的同时，也丢弃了部分目标信息，因此如果直接利用时频综合等方法重构目标信号，将会导致重构的目标信号产生失真。本文引入通过压缩感知方法，从少数数据中重构出完整的目标信号。图8和图9分别给出了FRFT扫频滤波方法重构的目标信号时域波形和本文提出的联合时频分布和压缩感知方法重构的目标信号时域波形。从图8和图9中可以看出，本文方法能够有效重构目标信号，而FRFT扫频滤波方法重构的目标信号则有部分失真。

图10给出了两种方法重构目标信号的脉冲压缩结果。从图10中可以看出，FRFT扫频滤波方法能够抑制大部分假目标旁瓣，但是在真实目标主瓣附近仍有少量假目标旁瓣存在，如图中箭头所示。这会影响雷达对真实目标的检测，而本文方法则能够有效抑制假目标旁瓣。图11表示两种方法的SMSP干扰抑制性能曲线，横轴表示干扰抑制前输入信号的信干比，纵轴表示干扰抑制后输出信号的信干噪比，其中当输入信干比相同时，输出信干噪比越大，表明对干扰的抑制效果越好。从图11中可以看出，随着输入信号信干比的增大，两种算法的干扰抑制性能都有一定程度的提升。在相同的信干比条件下，以输入信干比等于时为例，本文方法的干扰抑制后输出信干噪比为19.55 dB, FRFT扫频滤波方法的输出信干噪比为3.59 dB，即本文方法的干扰抑制性能比FRFT扫频滤波方法要改善约16 dB。

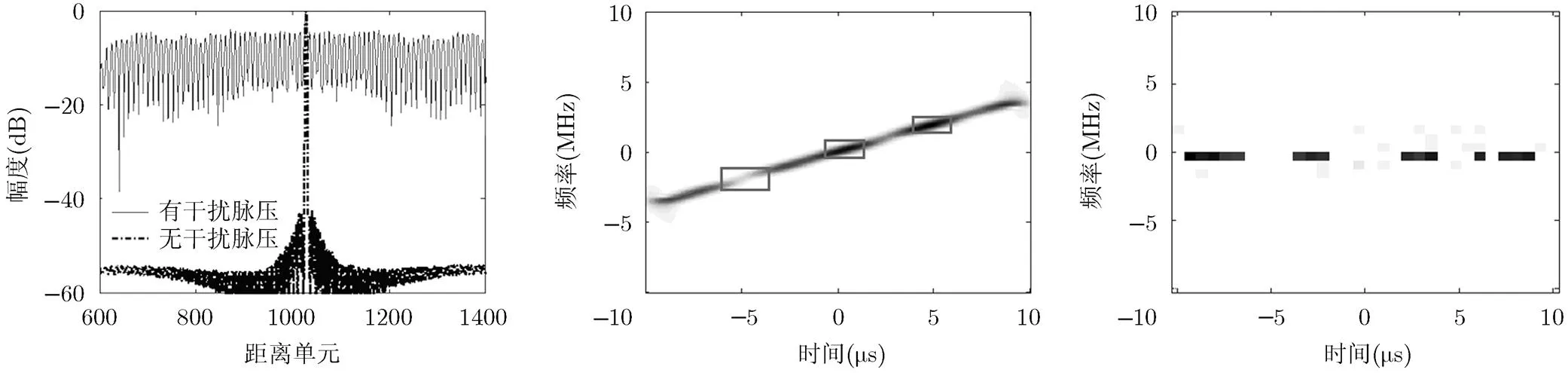
图5 雷达回波脉冲压缩结果     图6 FRFT干扰抑制后的时频分布    图7 筛选后保留的时频域信息

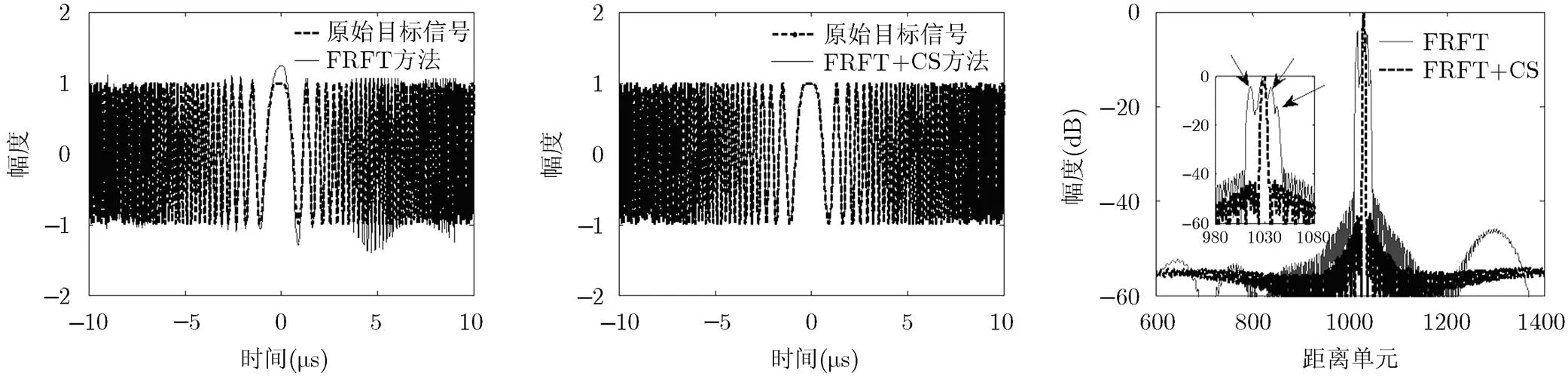
图8 FRFT方法重构信号的时域波形图  图9 FRFT+CS方法重构信号的时域波形图  图10 干扰抑制后的脉冲压缩结果

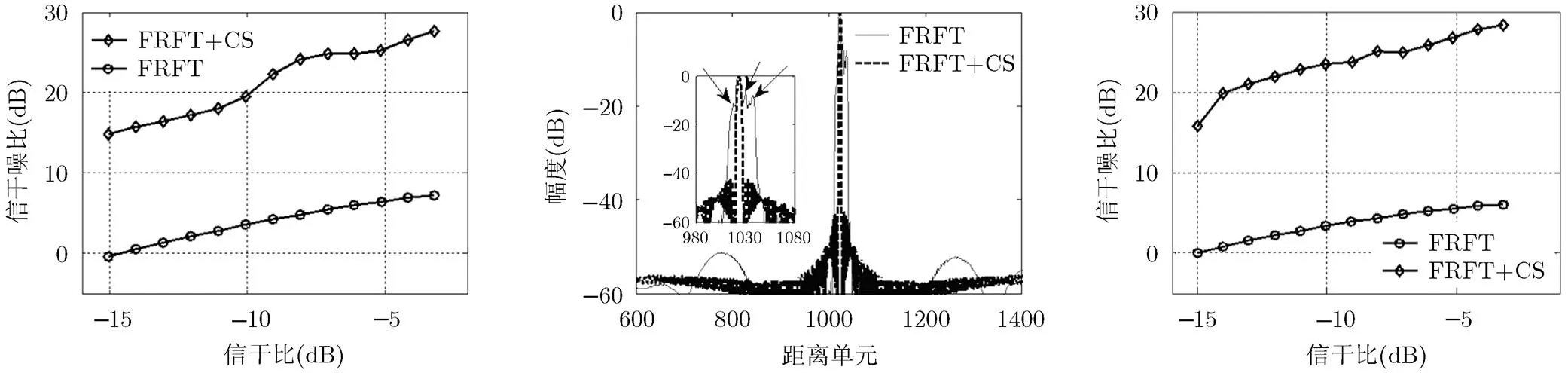
图11 干扰抑制性能曲线     图12 干扰抑制后脉冲压缩结果     图13 干扰抑制性能曲线

5 结束语

SMSP有源欺骗干扰能够在雷达输出端形成大量假目标进而影响雷达对真实目标的检测。本文通过分析SMSP干扰信号与目标信号在时频域上的能量分布特性，提出了联合时频分布和压缩感知的抗SMSP干扰策略。该方法通过在时频域丢弃SMSP干扰信号，并利用压缩感知方法精确重构目标信号，有效避免因重构目标信号失真而导致假目标旁瓣的产生。仿真数据表明了该方法理论分析的正确性，同时可以看出该方法有良好的抗干扰效果。

参考文献

[1] SPARROW M J and CIKALO J. ECM techniques to counter pulse compression radar[P]. United States Patent, 7081846, 2006.

[2] 卢云龙, 李明, 陈洪猛, 等. 基于奇异谱分析的抗数字射频存储距离波门拖引干扰[J]. 电子与信息学报, 2016, 38(3): 600-606. doi: 10.11999/JEIT150550.

LU Yunlong, LI Ming, CHEN Hongmeng,. Countering DRFM range gate pull-off jamming based on singular spectrum analysis[J].&, 2016, 38(3): 600-606. doi: 10.11999/JEIT150550.

[3] 卢云龙, 李明, 闫琰. 利用调频率匹配的DRFM欺骗干扰检测方法[J]. 西安电子科技大学学报, 2014, 41(5): 67-73. doi: 10.3969/j.issn.1001-2400.2014.05.012.

LU Yunlong, LI Ming, and YAN Yan. Method for detecting DRFM deception jamming based on LFM rate matching[J]., 2014, 41(5): 67-73. doi: 10.3969/j.issn.1001-2400.2014.05.012.

[4] ZHANG Jingdong, ZHU Daiyin, and ZHANG Gong. New antivelocity deception jamming technique using pulses with adaptive initial phase[J]., 2013, 49(2): 1290-1300. doi: 10.1109/TAES.2013.6494414.

[5] 吴亿锋, 王彤, 吴建新, 等. 基于广义旁瓣相消的机载雷达抗密集转发式干扰方法[J]. 电子与信息学报, 2014, 36(5): 1049-1054. doi: 10.3724/SP.J.1146.2013.01040.

WU Yifeng, WANG Tong, WU Jianxin,. A method to suppress dense repeater jamming for airborne radar based on generalized sidelobe canceller[J].&, 2014, 36(5): 1049-1054. doi: 10.3724 /SP.J.1146.2013.01040.

[6] 姜磊, 王彤. 机载雷达自适应发射技术抗相干转发式干扰[J]. 系统工程与电子技术, 2015, 37(4): 789-794. doi: 10.3969/ j.issn.1001-506X.2015.04.11.

JIANG Lei and WANG Tong. Airborne radar adaptive transmit technique for anti coherent repeater jammer[J]., 2015, 37(4): 789-794. doi: 10.3969/j.issn.1001-506X.2015.04.11.

[7] 同亚龙, 王彤, 代保全, 等. 一种抗密集欺骗式干扰的机载雷达动目标检测方法[J].电子与信息学报,2015, 37(3): 658-664. doi: 10.11999/JEIT140679.

TONG Yalong, WANG Tong, DAI Baoquan,. A moving target detection method to suppress dense deception jamming for airborne radar[J].&,2015, 37(3): 658-664. doi: 10.11999/ JEIT140679.

[8] 杨少奇, 田波, 李欣, 等. 基于时频图像特征提取的LFM雷达有源欺骗干扰识别[J]. 空军工程大学学报, 2016, 17(1): 56-59. doi: 10.3969/j.issn.1009-3516.2016.01.011.

YANG Shaoqi, TIAN Bo, LI Xin,. A recognition method of LFM radar active deception jamming based on SPWVD figure[J]., 2016, 17(1): 56-59. doi: 10.3969/j.issn.1009-3516.2016.01.011.

[9] ZHAO Yuan, DU Dongping, AHMED ABDALLA Ali,. Detection of SMSP jamming in netted radar system based on fractional power spectrum[C]. IEEE 17th International Conference on Computational Science and Engineering, Chendu, 2014: 989-993. doi: 10.1109/CES.2014.197.

[10] LI Yongping, YING Xiong, and TANG Bin. SMSP jamming identification based on matched signal transform[C]. IEEE International Conference on Computational Problem-Solving, Chendu, 2011: 182-185. doi: 10.1109/ICCPS.2011.6092274.

[11] SUN Minghong and TANG Bin. Suppression of smeared spectrum ECM signal[J]., 2009, 32(3): 407-413. doi: 10.1080/02533839. 2009.9671521.

[12] STANKOVIC L, THAYAPARAN T, DAKOVIC M,. Micro-Doppler removal in the radar imaging analysis[J]., 2013, 49(2): 1234-1250. doi: 10.1109/TAES.2013.6494410.

[13] WHITELONIS N and LING Hao. Radar signature analysis using a joint time-frequency distribution based on compressed sensing[J]., 2014, 62(2): 755-763. doi: 10.1109/TAP.2013. 2291893.

[14] 方标, 黄高明, 高俊, 等. FRFT域LFM雷达回波信号的压缩采样模型[J]. 西安电子科技大学学报, 2015, 42(1): 200-206. doi: 10.3969/j.issn.1001-2400.2015.01.032.

FANG Biao, HUANG Gaoming, GAO Jun,. Compressive sensing of linear frequency modulated echo signals in fractional fourier domains [J]., 2015, 42(1): 200-206. doi: 10.3969/j.issn.1001- 2400.2015.01.032.

[15] 闫浩, 董春曦, 赵国庆. 基于压缩感知的线性调频信号参数估计[J]. 电波科学学报, 2015, 30(3): 449-456. doi: 10.13443/ j.cjors.2014070103.

YAN Hao, DONG Chunxi, and ZHAO Guoqing. Parameter estimation of LFM signal based on compressed sensing[J]., 2015, 30(3): 449-456. doi: 10.13443/j.cjors.2014070103.

[16] ZUO Lei, LI Ming, ZHANG Xiaowei,. CFAR detection of range-spread targets based on the time-frequency decomposition feature of two adjacent returned signals[J]., 2013, 61(24): 6307-6319. doi: 10.1109/TSP.2013.2282274.

[17] 张玉恒, 吴启晖, 王金龙. 基于时频加窗短时傅里叶变换的LFM干扰抑制[J]. 电子与信息学报, 2007, 29(6): 1361-1364.

ZHANG Yuheng, WU Qihui, and WANG Jinlong. LFM interference suppression using time-frequency windowed short-time fourier transform[J].&, 2007, 29(6): 1361-1364.

[18] DJUROVIC I, STANKOVIC L, and BOHME J F. Robust L-estimation based forms of signal transforms and time-frequency representations[J]., 2003, 51(7): 1753-1761. doi: 10.1109/ TSP.2003.812739.

[19] STANKOVIC L, OROVIC I, STANKOVIC S,. Compressive sensing based separation of nonstationary and stationary signals overlapping in time-frequency[J]., 2013, 61(18): 4562-4572. doi: 10.1109/TSP.2013. 2271752.

卢云龙： 男，1986年生，博士生，研究方向为雷达抗干扰、雷达目标检测.

李 明： 男，1965年生，博士，教授，博士生导师，从事雷达图像处理与分析、宽带信号处理与微弱目标检测、高速并行信号处理、高性能DSP应用系统设计、雷达抗干扰技术等.

曹润清： 男，1988年生，博士，研究方向为非平稳信号参数估计、雷达目标检测.

王泽玉： 女，1990年生，博士，研究方向为微弱目标检测.

陈洪猛： 男，1986年生，博士，研究方向为SAR成像、目标检测.

Jointing Time-frequency Distribution and Compressed Sensing for Countering Smeared Spectrum Jamming

LU Yunlong LI Ming CAO Runqing WANG Zeyu CHEN Hongmeng

(,,710071,)

The SMeared SPectrum (SMSP) jamming is a special active deception jamming for countering a Linear Frequency Modulated (LFM) pulse compression radar system. For suppressing the SMSP jamming, a novel anti-jamming approach is proposed based on jointing Time-Frequency (TF) distribution and Compressed Sensing (CS). First the SMSP jamming is isolated in the TF domain, and then the TF points belonging to target signal are reserved. According to the linear relationship between the reserved TF points and the frequency domain of radar echo, a CS minimization model is established and the Orthogonal Matching Pursuit (OMP) algorithm is utilized to recover the target signal, which means the SMSP jamming is mitigated simultaneously. The validity of the proposed method is evaluated using experimental data via Monte Carlo simulation.

Active deception jamming; Jamming suppression; Time-frequency analysis; Compressed sensing

TN974

A

1009-5896(2016)12-3275-07

10.11999/JEIT160919

2016-09-12；改回日期：2016-11-25；

2016-12-13

卢云龙 yllu@stu.xidian.edu.cn

国家自然科学基金(61271297, 61272281, 61301284)，博士学科点科研专项基金(20110203110001)

The National Natural Science Foundation of China (61271297, 61272281, 61301284), The Specialized Research Fund for the Doctoral Program of Higher Education (20110203 110001)