贝叶斯膨胀算法对EnSRF雷达资料同化的影响研究
高士博 闵锦忠 黄丹莲
贝叶斯膨胀算法对EnSRF雷达资料同化的影响研究
高士博1, 2闵锦忠1, 2黄丹莲1, 2
1南京信息工程大学气象灾害预报预警与评估协同创新中心,南京 210044;2南京信息工程大学气象灾害教育部重点实验室,南京210044
本文针对2009年6月5日发生在我国华东地区的一次中尺度对流过程(Mesoscale Convective System,简称MCS),基于集合均方根滤波(Ensemble Square Root Filter,简称EnSRF)方法同化多部多普勒天气雷达资料,引入具有时空自适应理论优势的贝叶斯膨胀算法,通过与常数膨胀算法的对比,分析了两种膨胀算法对EnSRF同化效果的影响。结果表明:贝叶斯膨胀算法同化的雷达组合反射率因子在强对流中心处有所增强,改善了基于常数膨胀算法的EnSRF同化强对流系统偏弱的问题。相比常数膨胀算法,贝叶斯膨胀算法同化的冷池结构更合理,径向风和反射率因子的均方根误差均减少。进一步探讨贝叶斯膨胀算法对同化效果改善的原因,结果发现:贝叶斯膨胀参数的分布与反射率因子的均方根误差分布十分吻合,这表明贝叶斯膨胀算法可以在背景场均方根误差较大,即背景场与观测差距较大时,给出较大的膨胀参数,进而增加集合的背景场误差,使得观测权重增大,从而给出了较大的分析增量。对集合平均分析场进行了1小时的确定性预报发现,贝叶斯膨胀算法提高了预报模式对安徽与江苏交界处的强对流系统的模拟效果,回波强度更强,冷池强度和范围更大,且对于不同组合反射率因子的阀值,贝叶斯膨胀算法的评分(Equitable Threat Score,简称ETS)均高于常数膨胀算法。这表明贝叶斯膨胀算法有效地改进了基于常数膨胀算法的EnSRF同化雷达资料的效果。
集合卡尔曼滤波 雷达资料同化 贝叶斯膨胀算法 常数膨胀算法
1 引言
中尺度对流系统(Mesoscale Convective System,简称MCS)是水平尺度在2~2000 km左右的具有旺盛对流运动的天气系统,在卫星云图上表现为一块连续的高亮的云团,且具有对流核的云结构(Houze, 1993),在雷达回波图上,回波强度超过40 dB,伸展范围大于100 km,持续时间为3~24 h(Schumacher and Johnson, 2005)。MCS是产生雷暴、大风、暴雨和冰雹等强对流灾害性天气的重要天气系统,因此对其进行准确地预报就显得尤为重要。对于中尺度对流天气的数值预报和模拟,初值的获取很重要,而高时空分辨率的多普勒雷达资料包含了丰富的中小尺度信息,为数值天气预报(Numerical Weather Prediction,简称NWP)模式提供了合理和准确的初始场。
多普勒天气雷达观测的是非常规气象数据,需要从探测到的径向风和反射率因子来估计实际大气的状态,得到风、温、压、湿等模式变量信息。目前主要的雷达资料同化方法有三维、四维变分法和集合卡尔曼滤波(Ensemble Kalman Filter,简称EnKF)等。EnKF结合了传统卡尔曼滤波和集合预报的优点,通过预报集合样本估计得到具流依赖的背景误差协方差,与变分同化方法相比,EnKF算法简单,不要求编写切线性和伴随模式,而且可以显式地提供集合预报的初始扰动,已经成为国内外热门的资料同化方法(许小永等, 2006; Evensen, 2003; Zhang et al., 2003; Houtekamer and Mitchell 2005; Szunyogh et al., 2008; Torn and Hakim, 2008; Aksoy et al., 2009, 2010; Bonavita et al., 2010; 秦琰琰等, 2012)。近年来,很多学者将EnKF应用到对流尺度的资料同化上,如Snyder and Zhang(2003)利用EnKF同化模拟雷达资料,初步证明了将EnKF应用于对流尺度上同化雷达资料是可行的。Tong and Xue(2005)和 Xue et al.(2006)在此基础上进一步考虑了包含复杂冰相作用的微物理过程,利用ARPS(Advanced Regional Prediction System)模式及其EnKF系统同化了一次风暴过程的多普勒雷达资料,取得了较好的效果。Huet al.(2006a, 2006b)发现同化雷达资料能够更加准确地预报龙卷的位置,并且反射率的作用更加明显。兰伟仁等(2010)利用模拟多普勒雷达资料进行一系列风暴尺度的EnKF敏感性试验,检验EnKF在风暴天气尺度资料同化方面的效果,并分析了集合卡尔曼滤波各参数对同化效果的影响。
需要注意的是,尽管EnKF在对流尺度同化上取得了较好的效果,但它在实际雷达资料同化的应用中,还是不可避免产生滤波发散的问题。EnKF是通过集合来统计观测增量与集合扰动之间的相关系数的,当集合成员数较小时,相关系数会存在较大的采样误差。另外,由于数值模式的不确定性,模式积分预报和参数化的物理过程会引入模式误差(Miyoshi et al., 2011)。在EnKF 中若不能正确考虑采样误差和模式误差,预报集合的统计协方差将低估真正的预报误差协方差,集合离散度会迅速减少,使得观测对同化的影响越来越小,甚至完全失效,造成滤波发散(Houtekamer and Mitchell, 1998; Anderson and Anderson, 1999; Constantinescu, et al. 2007)。为此,一种旨在处理采样误差和模式误差的协方差膨胀技术逐渐发展起来。
最早Anderson and Anderson(1999)提出具有经验性质的协方差膨胀算法,即通过一个略大于1的膨胀参数来增大背景误差协方差,但膨胀参数的选择依赖集合成员数和分析的时间间隔等,需要反复试验才能得到,在复杂的NWP模式中,计算代价巨大。膨胀参数在时间和空间上都是常数,在观测稀少的地方会产生多余的离散度。随后,Zhang et al.(2004)采用了同时保留先验扰动和后验扰动的松弛膨胀技术,这种方法避免了对没有观测同化更新的集合扰动进行不必要的方差扩张。Whitaker et al.(2008)以及Houtekamer et al.(2009)发现,若对先前的分析成员添加随机的扰动,能够较好地处理协方差低估的不均匀性。然而,以上方法均需事先给定最优的参数,如振幅和权重系数等。另外,当天气系统发展变化快、观测信息密度比较大时,对所有变量使用空间一致的膨胀参数并不合理,在实际应用中误差的特性在空间上是各项异性的。近年来,气象学者致力于发展具有自适应性质的协方差膨胀算法(Miyoshi, 2011; Li et al. 2009; Bishop and Hodyss, 2009a, 2009b)。Anderson(2007)提出一种自适应协方差膨胀算法,膨胀参数的计算公式与贝叶斯滤波更新方程类似,寻找在已知观测的条件下最有可能出现的期望值,下一时次同化的膨胀参数为上一时次计算得到的期望值。该膨胀参数在时间上具有自适应性,但没有考虑膨胀参数在模式空间上的不均匀性。为此,Anderson(2009)进一步利用泰勒级数展开,先求解膨胀参数的观测似然函数,再计算贝叶斯膨胀参数的后验概率的极大值得到最佳的膨胀参数,从而实现了膨胀参数在时间和空间上的自适应,但该膨胀算法只是在简单的Lorenz_ 96进行试验。
由于集合平方根滤波(Ensemble Square Root Filter,简称EnSRF)方法能够避免传统EnKF由于扰动观测而造成的采样误差(Whitaker and Hamill, 2002),因此本文通过ARPS EnSRF系统,针对一次MCS的发生发展过程,将Anderson(2009)提出的具有时空自适应理论优势的贝叶斯膨胀算法应用到EnSRF雷达资料同化上,通过与常数膨胀算法的对比,全面评估了贝叶斯膨胀算法在EnSRF雷达资料同化上的适用性。
2 膨胀算法
(1)常数膨胀算法
Anderson andAnderson(1999)提出的常数膨胀算法公式为

其中,表示模式变量,上标inf表示进行了协方差膨胀,下标表示第个集合成员,下标表示第个模式变量,表示模式变量的总数,表示集合成员总数。是根据经验决定的协方差膨胀参数,不随时间变化,这对于发展变化比较快的中尺度天气系统是不合理的。另外,在空间上也是各向均匀的,在观测稀疏的区域会给出多余的离散度,导致模式积分不稳定,而在观测稠密的区域又会给出较低的离散度,从而降低同化效果。
(2)贝叶斯膨胀算法
Anderson(2009)进一步提出贝叶斯膨胀算法,基本膨胀公式形式与公式(1)相同,不同的是依据贝叶斯理论来估计膨胀因子的概率分布,通过令其后验概率分布取得极大值,最终求解得到膨胀参数值。
由贝叶斯公式,膨胀参数的后验概率为
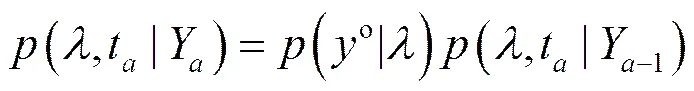
其中,表示概率密度函数,表示当前时刻,表示由模式分析值计算出的观测变量,中表示观测变量,上标o表示实际观测,下标表示当前时刻经过同化后的值,下标−1表示前一个时刻的分析值。假设先验概率分布符合正态分布,即其概率密度函数为
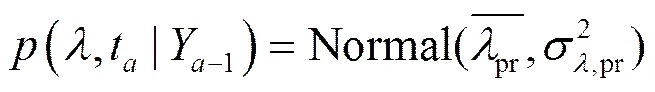
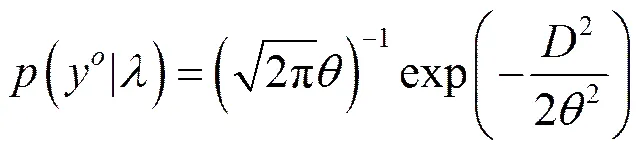
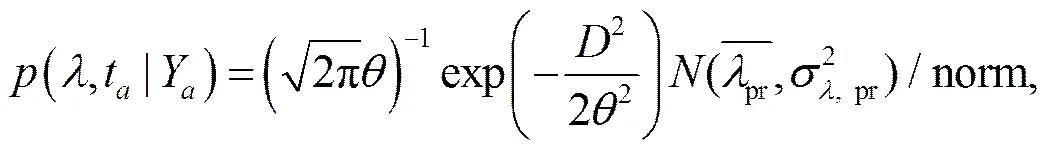
在时间自适应的基础上,进一步考虑膨胀参数在模式空间和观测空间的关系,引入观测空间膨胀参数。其中与的关系为:,表示数学期望,为观测和状态量的相关系数与局地化因子的乘积。通过可以建立膨胀参数在模式空间和观测空间的关系,从而实现了膨胀参数在时间和空间上的自适应。
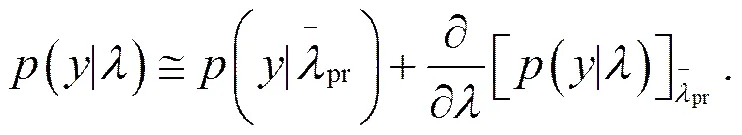
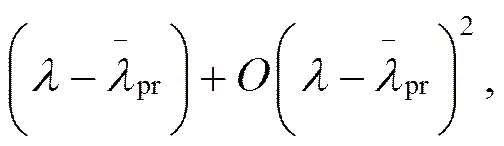
公式(6)可简化为
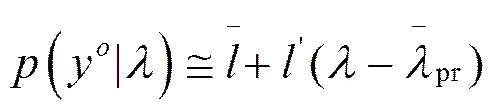
其中,
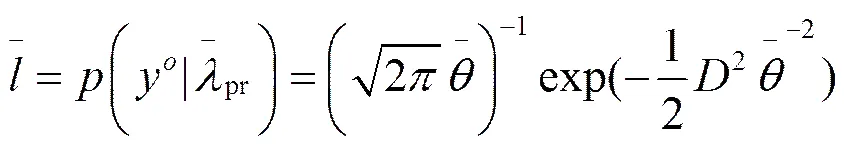
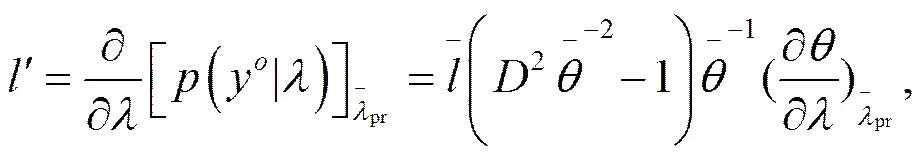
公式(7)、(8)、(9)中:




即. (14)
由上可知,根据公式(6)到(14)求得的贝叶斯膨胀参数能够根据观测而改变,是格点,变量和时间的函数,且是在采样误差最小化的意义下理论上的最优解,因此具有时空自适应的理论优势。
3 试验设计
2009年6月5日,华东地区发生一次典型的MCS过程,大部分地区出现强雷暴天气,部分地区伴随大风、冰雹,过程期间有35个站点降水强度超过10 mm h−1,9个站点超过20 mm h−1。这次MCS过程系统移动快,影响范围广,造成了非常严重的人员伤亡和财产损失。
本文采用非静力中尺度数值模式ARPS对此次MCS过程进行数值模拟,将NCEP(National Centers for Environmental Prediction)提供的6小时间隔,水平分辨率为0.5°×0.5°的GFS(Global Forecast System)资料作为初始和边界条件,同时利用EnSRF同化方法对4部S波段天气雷达,包括南京、盐城、南通以及合肥进行雷达资料同化。在进行多普勒雷达资料同化之前,需要对雷达资料进行质量控制,包括去除噪声点、地物回波、二次回波、速度退模糊(Oye et al., 1995)和去距离折叠。最后将质量控制后的雷达资料插值到模式网格上,在插值过程中进行了雷达观测资料的稀疏化。
为比较不同膨胀算法对雷达资料同化效果的影响,分别设计三组试验(表1)。三组试验均采用双层单向嵌套网格,外层网格水平分辨率为3 km,水平格点数为303×303,内层网格水平分辨率为 1 km,水平格点数为803×803。两层嵌套的中心均位于(33°N,120°E),垂直方向均取53个不等距分层,垂直平均分辨率为425 m。两层区域均覆盖中国江苏、安徽、山东和浙江大部分地区,地形分辨率为30 s(图1),且均采用Lin-Tao冰相微物理参数化方案(Hong et al., 2004),1.5阶湍流动能方案,NASA大气辐射传输方案和两层土壤模式等,内外层区域均不使用积云对流参数化方案。ARPS模式只能实现单向嵌套,所以内层区域的模拟是以外层区域的模式输出资料作为侧边界条件的。
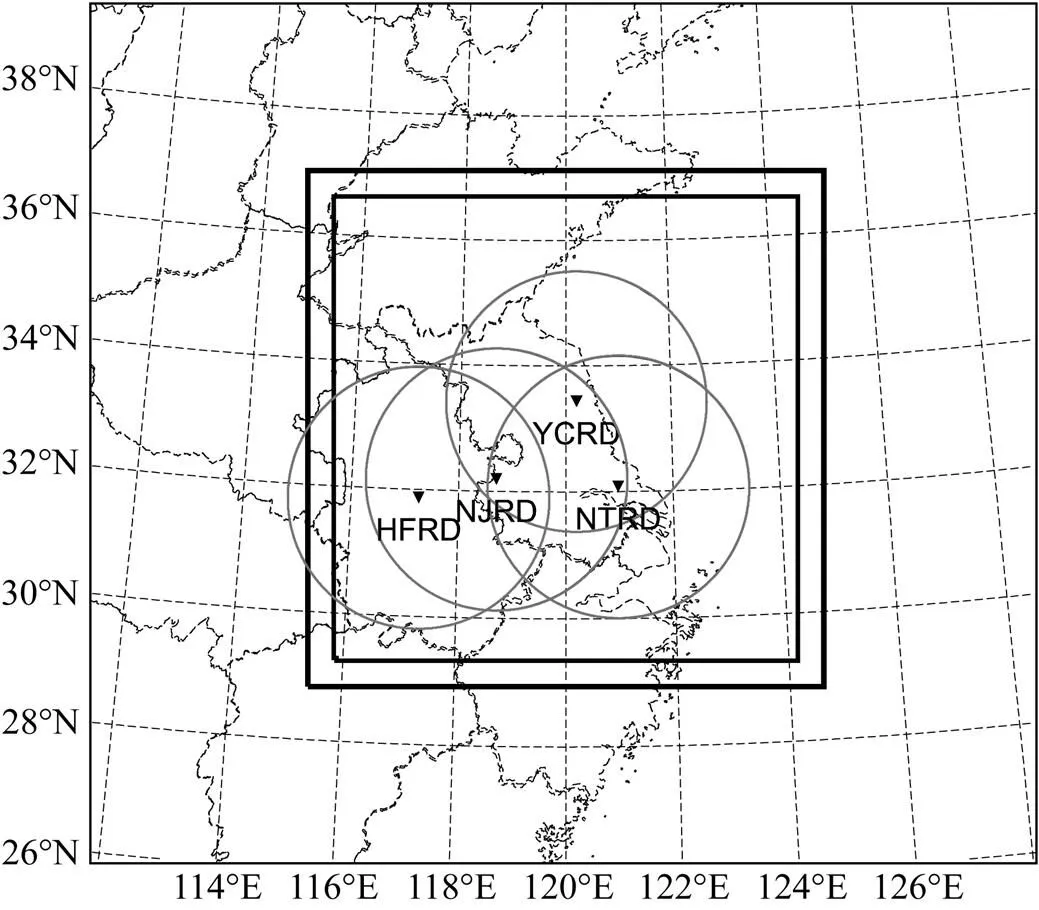
图1 模拟区域与雷达位置(图中黑色矩形框代表模拟范围,倒三角代表雷达位置,大圆圈为半径为230 km雷达观测的范围,其中4部雷达分别为南京(NJRD)、南通(NTRD)、盐城(YCRD)和合肥(HFRD)雷达

表1 试验方案
第一组试验为控制试验(Experiment of Control,简称ExpC),只模拟不同化,外层区域采用6小时间隔的GFS再分析资料作为初始场和边界条件,从6月5日09:00 UTC(协调世界时,下同)开始模拟,积分2 h,将10:00 UTC的模拟结果插值到内层区域,并利用外层区域提供的侧边界条件,对内层区域进行模拟,从10:00 UTC模拟到11:00 UTC。
第二组试验为常数膨胀算法同化试验(Experiment of Multipicative inflation, 简称ExpM),首先对6月5日00:00 UTC的外层区域先进行9小时“spin up”积分再同化,然后在5日09:00 UTC的预报场加入初始扰动后产生40个集合成员。参考Putnam et al.(2014)的方法,进行了两次高斯随机平滑扰动。表2为两次高斯随机平滑扰动的平滑半径和变量扰动的标准差,可以看出,第一次扰动在是全场范围内进行的振幅较小的扰动,由于扰动强度较弱,平滑半径较小。对全场进行扰动是因为MCS在发展过程不断有新的对流区域生成,可以使每个格点处的集合离散度都大于0。第二次扰动是在对流区域(≥10 dB)范围进行振幅较大扰动,由于扰动强度较强,所以平滑半径较大,在对流区域进行较强的扰动是因为在对流区域存在较大的误差,包括风场,温度和水物质等。09:06 UTC开始同化雷达资料,每6分钟同化一次,10:00 UTC结束同化。协方差局地化为五阶距离相关函数方案(Gaspari and Cohn, 1999),水平距离为8 km,垂直距离为4 km,协方差膨胀算法为常数膨胀算法,最后在内层区域上对10:00 UTC的集合平均分析场进行1小时的确定性预报。
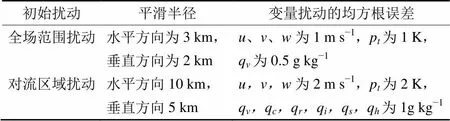
表2 初始扰动方案
注:、、分别为扰动风场的纬向分量,经向分量,垂直分量p为扰动位温q为水汽混合比q为云水混合比q为雨水混合比q为冰晶混合比q为雪混合比q为冰雹混合比
第三组试验为贝叶斯膨胀算法试验(Experiment of Bayes inflation,简称ExpB),设计同第二组试验,不同的是采用贝叶斯自适应膨胀算法,同样对EnSRF的集合平均分析场的进行1小时的确定性预报。
4 试验结果
4.1 观测与模拟分析
从观测雷达组合反射率因子随时间的演变可以看出(图2),2009年6月5日09:00 UTC,MCS主体部分位于江苏省和山东南部,内含许多小尺度的对流单体,最强回波强度在60 dB以上。在MCS主体的西侧,即江苏与安徽交界处,存在一条呈西北—东南走向的线状强对流回波区,南北方向的长度约为400 km,东西方向的宽度约为20 km。在MCS主体的南侧,强对流回波中心为弓形,其中在上海附近的最强回波强度达60 dB以上。此外,在合肥附近还存在一条尺度较小的对流系统向东北方向移动,且在移动的过程中,前方不断有新的对流单体生成。可见,MCS分别在江苏和合肥附近存在两个孤立的对流系统。5日09:30 UTC,这两个对流系统进一步加强,合肥和上海附近的50 dB以上的强对流回波区范围明显增大。5日10:00 UTC,合肥附近的对流系统与MCS主体西侧的对流单体逐渐靠拢,半小时后,形成一条东西跨度更大的强对流回波区,同时在MCS主体南侧的弓形回波面积增大,层云区结构更紧致,但MCS主体中部的回波强度有所减弱。5日11:00 UTC,MCS主体南部的弓形回波发展成熟,具有高度的组织性,而新形成的强对流系统范围开始减弱,结构变松散。图3为控制试验模拟的雷达组合反射率因子,与图2a–e对比可知,控制试验模拟的MCS与观测有较大的偏差,基本没有模拟出MCS主体的位置和结构。在山东和江苏交界处模拟出的单体偏强,位于江苏南部的弓形回波没有模拟出来。在合肥附近模拟的对流单体组织松散,面积偏小。

图2 2009年6月5日雷达观测组合反射率因子(单位:dBZ):(a)09:00(协调世界时,下同);(b)09:30;(c)10:00;(d)10:30 ;(e)11:00
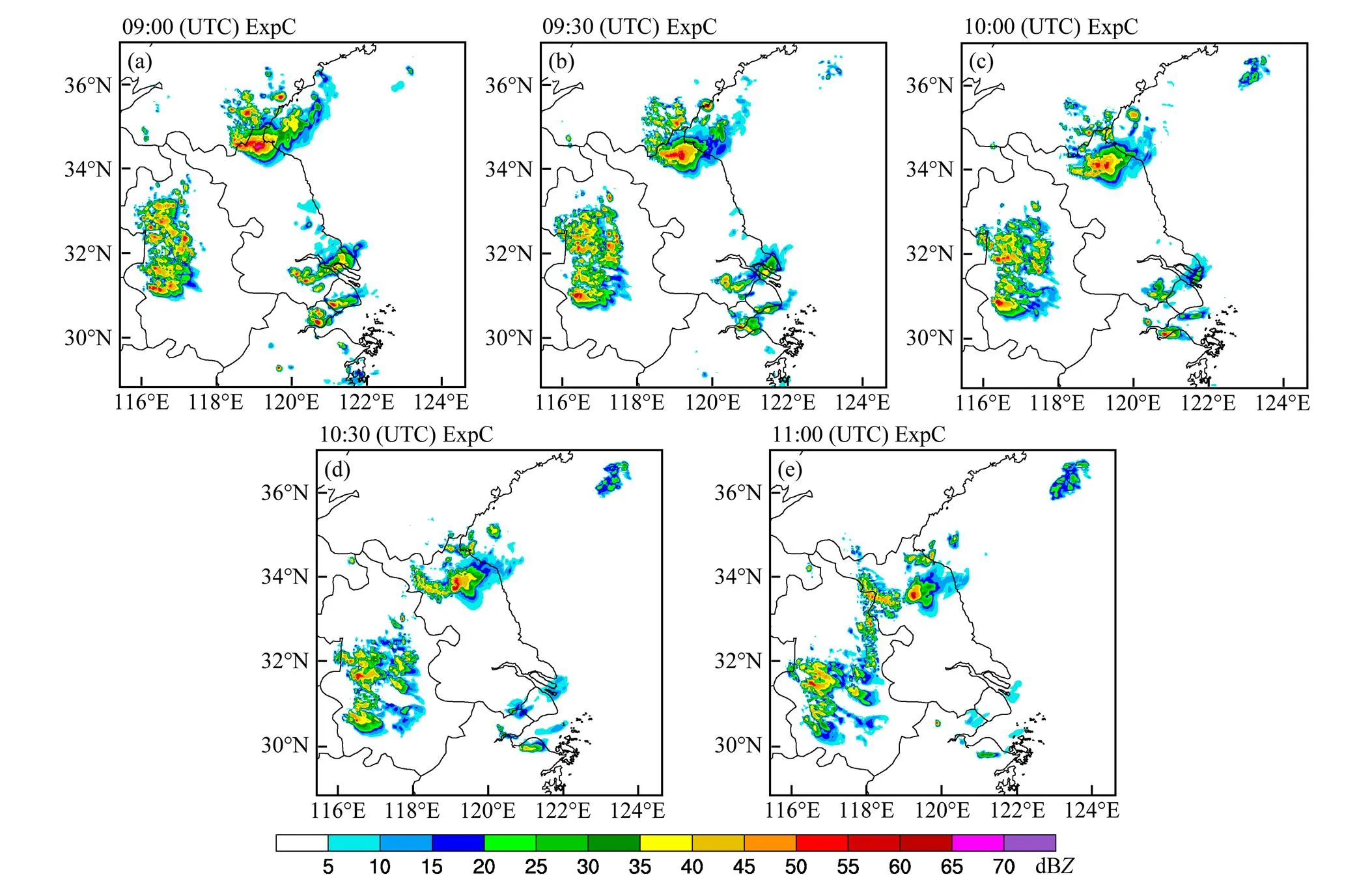
图3 同图2,但为模式模拟
4.2 同化结果分析
以上述分析表明,控制试验只能模拟出部分强对流回波区,与观测有较大的偏差。图4分别基于常数膨胀算法和贝叶斯膨胀算法同化得到集合平均场。对比图4a–f与图3b、c可以发现,两组同化试验的组合反射率因子与实况图在空间上十分相似,明显优于控制试验,这说明EnSRF有效地同化了雷达资料,提高了初始场的准确程度。在5日09:30 UTC,两组试验均能分析出江苏境内团状的中尺度对流系统,其内部包含多个强度不同的对流云。在主对流系统的后部,即在合肥附近也同化出一个正在发展的对流单体向东北方向移动。相比ExpM,ExpB得到的对流单体和实况场更接近,尤其在合肥附近以及江苏和安徽交界处。在合肥(33°N,117°E)附近,ExpM同化的组合反射率因子偏弱,约55 dB,而ExpB为60 dB。另外,ExpB在江苏和安徽省交界处(33°N,119°E)线状结构明显,而ExpM在该处的对流范围偏小,强度偏弱。在5日10:00 UTC(图4d),合肥附近的对流单体并入MCS主体,且团状MCS的强度继续加强,雷达回波强度有所增强,水平覆盖面积也增大。总体来说,两种膨胀算法基本上同化出MCS的形状、强度和位置,但在其细节结构,尤其是强对流区域,ExpB得到的最强组合回波的范围相比ExpM明显增大,组织性也更强,ExpM得到的对流中心强度偏弱。

图4 2009年6月5日EnSRF分析的组合反射率因子(单位:dBZ):(a)09:30观测;(b)09:30贝叶斯膨胀试验;(c)09:30常数膨胀试验;(d)10:00观测;(e)10:00贝叶斯膨胀试验;(f)10:00常数膨胀试验
为了更清楚地看出不同膨胀算法同化效果的差异,图5a–d为ExpB与ExpM组合反射率因子与观测的偏差图。由图可知,两组试验在江苏和安徽的交界处存在负偏差,在山东和江苏的交界处存在正偏差。5日09:30 UTC时,相比于ExpM,ExpB与观测的负偏差的绝对值略小,在10:00 UTC时,ExpB的负偏差的绝对值进一步减小,且正偏差也有不同程度的减少。可见,贝叶斯膨胀算法通过减少采样误差,明显减少了与观测的偏差,且随着时间的增加更加明显。
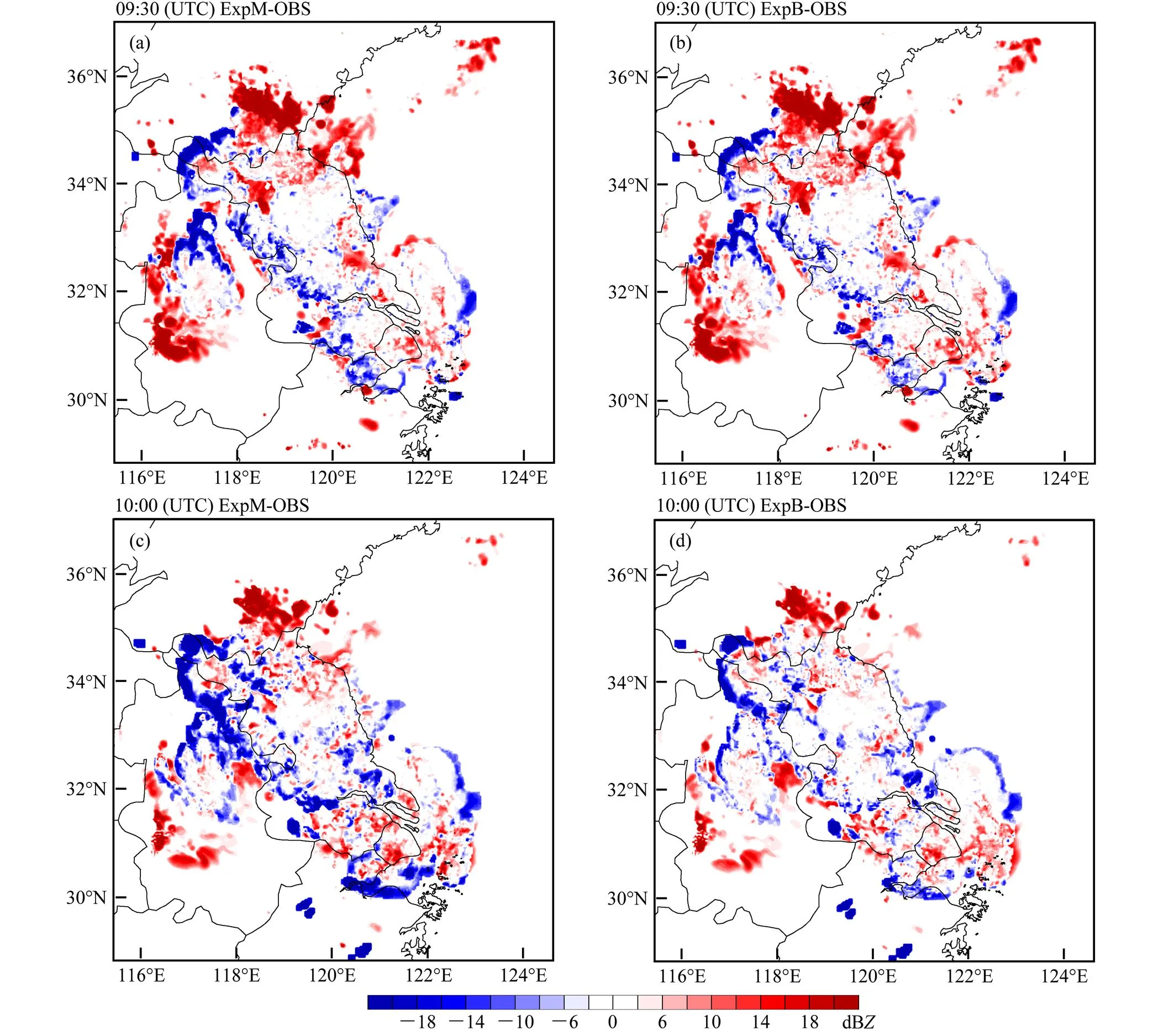
图5 2009年6月5日EnSRF分析的组合反射率因子与观测的差(单位:dBZ):(a)09:30常数膨胀试验与观测的差;(b)09:30贝叶斯膨胀试验与观测的差;(c)10:00常数膨胀试验与观测的差;(d)10:00贝叶斯膨胀试验与观测的差
冷池是由于降水蒸发冷却导致冷空气不断下沉扩展而形成的近地面冷空气堆(陈明轩等,2012)。冷池的强度和低层风切变是决定MCS强度和结构的主要因素,冷池的冷出流与低层环境风的辐合作用能够使对流运动长时间维持(张进和谈哲敏,2008)。从近地面扰动温度的模拟结果来看(图6a、b、d、e),在09:30 UTC,两组试验在江苏的大部以及江苏与安徽的交界处,近地面的扰动位温场均存在负中心,表明此时低层已经形成明显的冷池结构,其中最强冷池中心位于上海(30.3°N,121°E)和江苏与山东省交界处(34.2°N,119°E),最低扰动位温能达到-8 K。09:30 UTC时,在江苏和安徽交界处,ExpB的冷池强度略强于ExpM。由图6c可以看出,两者差值的强度和范围随时间增加。在10:00 UTC时,ExpB的冷池强度和面积明显强于ExpM(图6f)。由此可见,贝叶斯膨胀算法同化的冷池面积更大,强度更强,比常数膨胀算法更加合理。

图6 2009年6月5日EnSRF分析的地面扰动位温(单位:K)和水平速度(单位:m s−1):(a)09:30常数膨胀试验;(b)09:30贝叶斯膨胀试验;(c)09:30贝叶斯膨胀试验与常数膨胀试验的差;(d)10:00常数膨胀试验;(e)10:00贝叶斯膨胀试验;(f)10:30贝叶斯膨胀试验与常数膨胀试验的差
为了定量地对比分析不同试验分析场的误差,以合肥附近的雷达为例,图7分别计算了两组试验在同化前后径向风和反射率因子的均方根误差。由图可知,无论是哪组试验,预报误差在刚开始时均较大,同化雷达资料后,所有变量的分析误差在各个时刻均有不同程度的下降,这表明雷达资料同化有效地降低了预报误差。
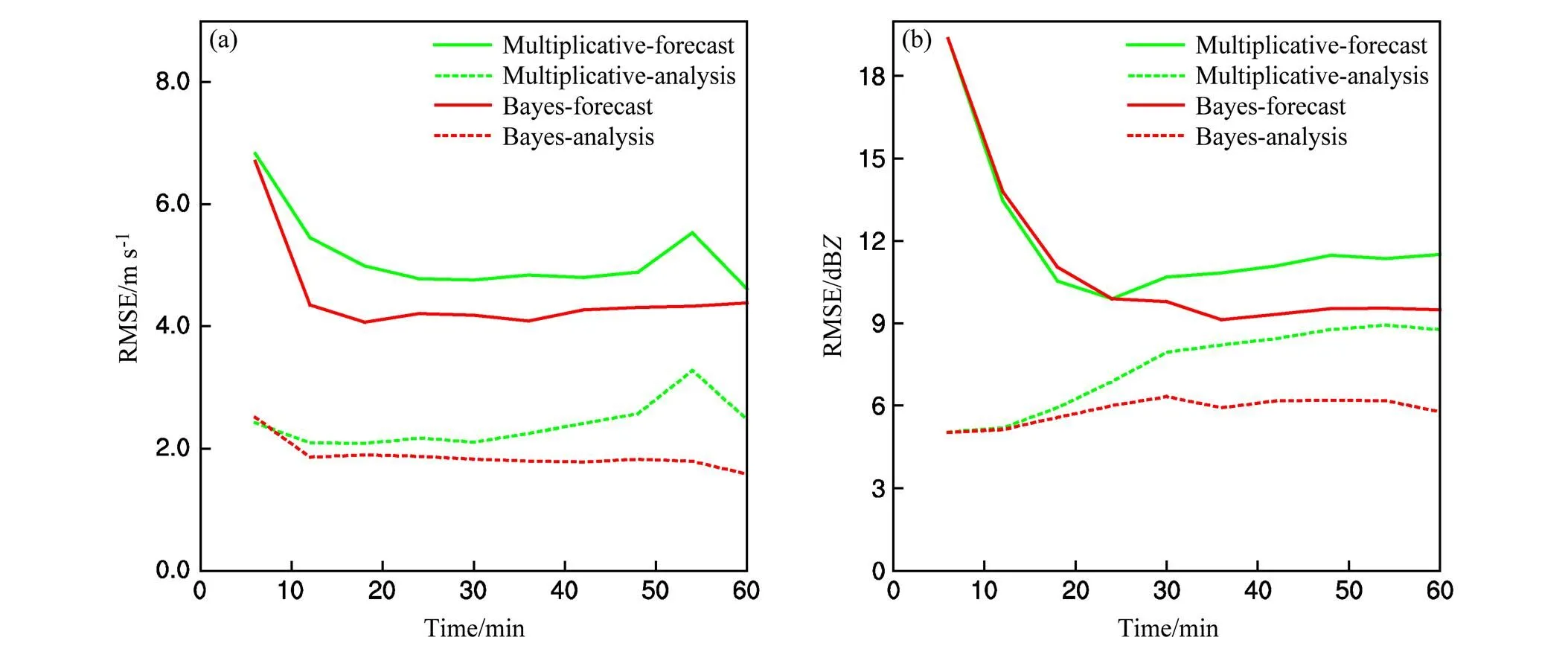
图7 2009年6月5日09:06 UTC至10:00 UTC EnSRF合肥雷达处的均方根误差(横轴为距离09:00 UTC的时长):(a)径向风(单位:m s−1);(b)反射率因子(单位:dBZ)
对比两组试验的预报和分析误差发现,无论是径向风还是反射率因子,ExpB的误差均小于ExpM。对于径向风的预报和分析误差,在第一次同化循环中,ExpB和ExpM误差均随时间迅速减少,之后趋于平缓。ExpB经过一次循环后,预报误差一直在4 m s−1以下,分析误差一直在2 m s−1以下。ExpM在48~54 min时,误差有个增加的过程,之后开始减少,预报误差减少至4.2 m s−1,分析误差减少至2.2 m s−1。对于反射率因子预报误差,ExpB和ExpM在前两次循环误差相差较少,均先随着 时间迅速减少。24 min后,ExpB和ExpM的误差趋于稳定,且随着时间的增加,ExpB误差明显 小于ExpM。对于反射率因子分析误差,ExpB和ExpM在前三次循环中缓慢增加,之后逐渐收敛,其中ExpB和ExpM分别收敛至5 m s−1和8 m s−1左右。
综上可知,采用自适应的贝叶斯膨胀算法试验得到的径向风和反射率因子的误差始终小于常数膨胀算法试验,径向风和反射率因子分别经过1和3次同化循环后,观测和模式变量场之间的协相关关系开始趋于合理,观测信息能够对预报场进行准确的调整,误差逐渐趋于稳定。
4.3 原因分析
以上分析表明,贝叶斯膨胀算法较常数膨胀算法有更明显的同化优势。为了探讨贝叶斯膨胀算法对同化效果改善的原因,图8以冰雹混合比变量为例,给出了贝叶斯膨胀参数的均方根在5 km处的水平结构。由图可见,在江苏与安徽的交界处和合肥附近,达到1.8以上,自适应的贝叶斯膨胀算法通过提高协方差膨胀参数,给与雷达观测更多的权重,改善了EnKF基于常数膨胀算法同化强对流系统偏弱的问题。需要注意的是,在MCS南部,两种试验模拟的弓形回波相比观测均偏强,结构也更紧致,主要体现在回波强度在40~45 dB之间的面积增大。因此该处不高,为1.1左右,这都说明贝叶斯膨胀参数的结构基本上是合理的,在时空上是不均匀的膨胀参数更符合实际情况。

图8 2009年6月5日EnSRF贝叶斯膨胀试验5 km处冰雹混合比的膨胀参数的均方根:(a)09:30;(b)10:00
图9进一步给出了ExpB在5 km处反射率因子的均方根误差空间分布。由图9可知,5日09:30 UTC,绝大部分地区MCS的反射率因子的均方根误差小于4 dB,但在合肥、安徽与江苏的交界处以及上海西部等地的均方根误差相对比较大,最大值发生在连云港,可达20 dB。5日10:00 UTC,均方根误差相对减少,在江苏南部、安徽与江苏的交界处大部分均方根误差在6 dB以下,但在部分区域,均方根误差依然较大,均超过10 dB。对比图8发现,ExpB的均方根误差的高值区对应的均大于1.8,这表明当模式背景场与观测差距较大时,贝叶斯膨胀算法通过给出较大的膨胀参数,给予观测更大的权重,使得模式背景场分析的反射率因子增强,从而更加接近观测。
4.4 模拟结果
以上分析表明,基于贝叶斯膨胀算法的EnSRF雷达资料同化,对MCS回波结构和强度具有明显地改善,且能够较准确地分析MCS的热力场和动力场的细致特征。为了从动力上进一歩验证贝叶斯膨胀方法的有效性,图10分别基于两种不同膨胀算法的EnSRF的集合平均分析场作了1小时的确定性预报。
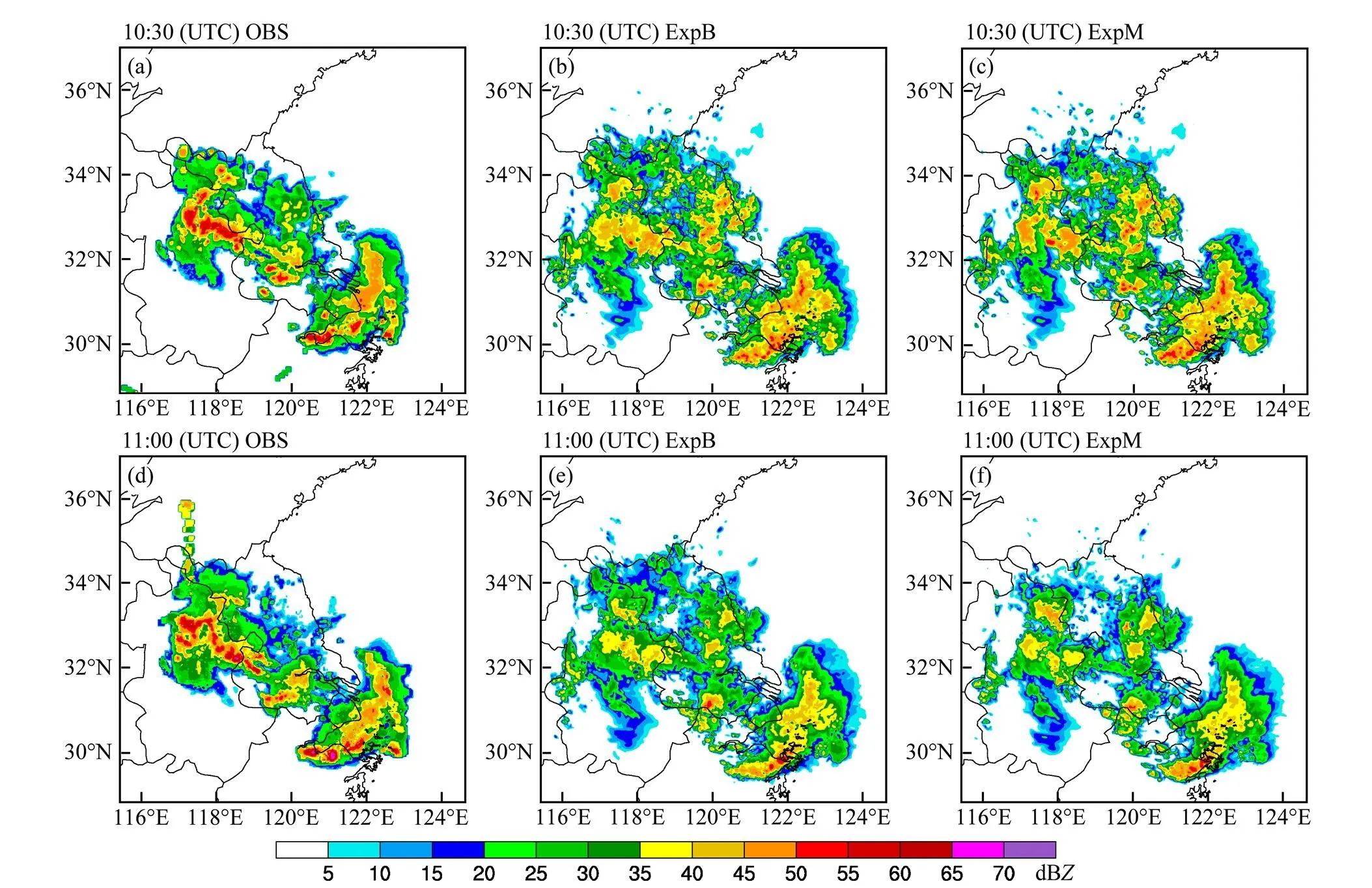
图10 基于EnSRF分析场模拟的组合反射率因子(单位:dBZ)2009年6月5日:(a)10:30观测;(b)10:30贝叶斯膨胀试验;(c)10:30常数膨胀试验;(d)11:00观测;(e)11:00贝叶斯膨胀试验;(f)11:00常数膨胀试验
5日10:30 UTC,在安徽与江苏交界处,已经形成一条有组织的西北东南走向的强对流回波带,且在外围有大范围的层状回波存在。MCS南部受较强西北风的影响,回波带呈现弯曲,中部向前突出,与MCS的移动方向一致,为典型的弓状回波。两组试验均较好地再现MCS南部的弓状回波,也基本模拟出其它对流单体的形状。在安徽和江苏交界处,相比雷达观测,ExpB模拟的对流带组合回波强度偏弱,约为45 dB,但组合回波已呈现组织化特征。ExpM在此处的组合回波强度约40 dB,对流带组织结构较差,出现两个孤立的对流中心。5日11:00 UTC弓状回波中的对流云有所增强,但强对流回波带和层状云稍减弱。两组试验基本上模拟出MCS的主要特征,尤其是南部弓状回波与观测十分接近,但在江苏盐城、南通模拟的组合回波偏强,范围偏大,结构变松散。在江苏和安徽处交界处,ExpB虽然模拟的对流带偏弱,但相比ExpM,组合回波大值区的面积增大,组织性更强。
ETS(Equitable Threat Score)评分是衡量某一等级的预报准确率的标准,ETS值越接近1,表明预报的准确率越高。表3给出了ExpM和ExpB在不同等级的组合反射率因子的ETS评分,从表中可以得到,ExpB在大于15、30和45 dB的回波强度的ETS时间平均值分别为0.6087626、0.4728514和0.2218793,ExpM在大于15、30和45 dB的回波强度的ETS时间平均值分别为0.5670509、0.4594605和0.1858251。在5日10:00 UTC和5日11:00 UTC之间,ExpB在弱回波区,次强回波区和强对流回波区的ETS评分均高于ExpM,表明贝叶斯膨胀算法试验在不同等级的回波强度的模拟水平均要高于常数膨胀算法试验。

表3 常数膨胀试验和贝叶斯膨胀试验的ETS评分
图11a、b、d、e给出了基于常数膨胀算法和贝叶斯膨胀算法模拟的扰动位温和水平速度场,可以看出,两组试验在江苏和安徽的交界处、山东与江苏的交界处、江苏的中北部以及上海附近存在冷池中心,其中以上海为中心的弓形回波的冷池强度最强。低层的冷池是对流的产物,比较两组试验发现,贝叶斯膨胀算法模拟的冷池状态与模拟的组合反射率因子趋于一致。10:30 UTC时,在江苏和安徽交界处,ExpB模拟的冷池强度约为-7 K,最低位温值的范围增大。ExpM模拟的冷池强度和范围均比ExpB小和弱,说明常数膨胀算法在此处模拟的对流偏弱。在11:00 UTC时,冷池进一步加强,在合肥、安徽和江苏省交界处的两块冷池中心已经合并为新的强冷池中心。由ExpB与ExpM扰动位温差值(图11c、f)也可以明显看出,贝叶斯膨胀算法试验比常数膨胀算法试验模拟的冷池中心更强。

图11 基于EnSRF分析场模拟的地面扰动位温(单位:K)和水平速度(单位:m s−1)2009年6月5日(a)10:30常数膨胀试验;(b)10:30贝叶斯膨胀试验;(c)10:30贝叶斯膨胀试验与常数膨胀试验的差(d)11:00常数膨胀试验;(e)11:00贝叶斯膨胀试验;(f)11:00贝叶斯膨胀试验与常数膨胀试验的差
5 结论
本文基于ARPS模式,针对2009年6月5日发生在我国华东地区的一次MCS过程,引入最新的贝叶斯膨胀算法到EnSRF雷达资料同化上,通过与常数膨胀算法的对比,探讨了两种膨胀算法对EnSRF同化效果的影响及其原因,并通过数值模拟,进一步验证了将贝叶斯膨胀算法应用于EnSRF同化雷达资料的可行性,主要得到以下结论:
(1)贝叶斯膨胀算法同化出的对流单体强于常数膨胀算法,对流中心组合反射率因子增强,尤其在安徽与江苏交界处,合肥附近。贝叶斯膨胀算法得到的冷池结构更合理,存在两个明显的低温中心,常数膨胀算法给出的冷池强度偏弱,面积偏小。贝叶斯膨胀算法试验得到的径向风和反射率因子的误差始终小于常数膨胀算法试验。
(2)贝叶斯膨胀参数的空间分布与反射率因子的均方根误差的空间分布一致,反射率因子均方根误差的高值区对应的膨胀参数均大于1.8,这表明贝叶斯膨胀算法可以在背景场均方根误差较大,即背景场与观测差距较大时,给出较大的膨胀参数,进而增加集合的背景场误差,使得观测权重增大,从而给出了较大的分析增量。
(3)基于贝叶斯膨胀算法对中尺度对流系统回波强度、热力场和动力场的准确反演,对10次同化循环后的集合平均场开展预报试验。结果表明,与常数膨胀算法相比,雷达回波的强度和范围更大,冷池的结构更合理,尤其在安徽与江苏的交界处、合肥附近模拟效果较好。通过计算两种算法的ETS评分发现,贝叶斯膨胀算法的ETS评分普遍高于常数膨胀算法。
本文的分析表明,贝叶斯膨胀算法有效地改进了基于常数膨胀算法的EnSRF同化雷达资料的效果。这是因为贝叶斯膨胀算法具有时间和空间的自适应性的理论优势,能够使膨胀参数的时空分布特征随观测而变化,有效地改善了背景误差协方差的结构,从而改进了EnSRF的同化效果。
参考文献:(References)
Aksoy A, Dowell D C, Snyder C. 2009. A multicase comparative assessment of the ensemble Kalman filter for assimilation of radar observations. Part I: Storm-scale analyses [J]. Mon. Wea. Rev., 137 (6): 1805–1824, doi:10.1175/2008MWR2691.1.
Aksoy A, Dowell D C, Snyder C. 2010. A multicase comparative assessment of the ensemble Kalman filter for assimilation of radar observations. Part II: Short-range ensemble forecasts [J]. Mon. Wea. Rev., 138 (4): 1273–1292, doi:10.1175/2009MWR3086.1.
Anderson J L. 2007. An adaptive covariance inflation error correction algorithm for ensemble filters [J]. Tellus A, 59 (2): 210–224, doi:10.1111/ j.1600-0870.2006.00216.x.
Anderson J L. 2009. Spatially and temporally varying adaptive covariance inflation for ensemble filters [J]. Tellus A, 61 (1): 72–83, doi:10.1111/ j.1600-0870.2008.00361.x.
Anderson J L, Anderson S L. 1999. A Monte Carlo implementation of the nonlinear filtering problem to produce ensemble assimilations and forecasts [J]. Mon. Wea. Rev., 127 (12): 2741–2758, doi:10.1175/1520- 0493(1999)127<2741:AMCIOT>2.0.CO;2.
Bishop C H, Hodyss D. 2009a. Ensemble covariances adaptively localized with ECO-RAP. Part I: Tests on simple error models [J]. Tellus A, 61 (1): 84–96, doi:10.1111/j.1600-0870.2008.00371.x.
Bishop C H, Hodyss D. 2009b. Ensemble covariances adaptively localized with ECO-RAP. Part II: A strategy for the atmosphere [J]. Tellus A, 61 (1): 97–111, doi:10.1111/j.1600-0870.2008.00372.x.
Bonavita M, Torrisi L, Marcucci F. 2010. Ensemble data assimilation with the CNMCA regional forecasting system [J]. Quart. J. Roy. Meteor. Soc., 136 (646): 132–145, doi:10.1002/qj.553.
陈明轩, 王迎春, 肖现, 等2012. 基于雷达资料四维变分同化和三维云模式对一次超级单体风暴发展维持热动力机制的模拟分析 [J]. 大气科学, 36 (5): 929–944. Chen Mingxuan, Wang Yingchun, Xiao Xian, et al. 2012. A case simulation analysis on thermodynamical mechanism of supercell storm development using 3-D cloud model and 4-D variational assimilation on radar data [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 36 (5): 929–944, doi:10.3878/j.issn.1006-9895.2012.11132.
Constantinescu E M, Sandu A, Chai T F, et al. 2007. Ensemble-based chemical data assimilation. Part I: General approach [J]. Quart. J. Roy. Meteor. Soc., 133 (626): 1229–1243, doi:10.1002/qj.76.
Evensen G. 2003. The Ensemble Kalman Filter: Theoretical formulation and practical implementation [J]. Ocean Dyn., 53 (4): 343–367, doi:10.1007/ s10236-003-0036-9.
Gaspari G, Cohn S E. 1999. Construction of correlation functions in two and three dimensions [J]. Quart. J. Roy. Meteor. Soc., 125 (554): 723–757, doi:10.1002/qj.49712555417.
Hong S Y, Dudhia J, Chen S H. 2004. A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation [J]. Mon. Wea. Rev., 132 (1): 103–120, doi:10.1175/1520- 0493(2004)132<0103:ARATIM>2.0.CO;2.
Houtekamer P L, Mitchell H L. 1998. Data assimilation using an ensemble Kalman filter technique [J]. Mon. Wea. Rev., 126 (3): 796–811, doi:10.1175/1520-0493(1998)126<0796:DAUAEK>2.0.CO;2.
Houtekamer P L, Mitchell H K. 2005. Ensemble Kalman filtering [J]. Quart. J. Roy. Meteor. Soc., 131(613): 3269–3289, doi:10.1256/qj.05.135.
Houtekamer P L, Mitchell H K, Deng X X. 2009. Model error representation in an operational ensemble Kalman filter [J]. Mon. Wea. Rev., 137 (7): 2126–2143, doi:10.1175/2008MWR2737.1.
Houze R A Jr. 1993. Cloud Dynamics [C]. San Diego: Academic Press, 573pp.
Hu M, Xue M, Brewster K. 2006a. 3DVAR and cloud analysis with WSR- 88D Level-II data for the prediction of the Fort Worth, Texas, tornadic thunderstorms. Part I: Cloud analysis and its impact [J]. Mon. Wea. Rev., 134 (2): 675–698, doi:10.1175/MWR3092.1.
Hu M, Xue M, Gao J D, et al. 2006b. 3DVAR and cloud analysis with WSR-88D Level-II data for the prediction of the Fort Worth, Texas, Tornadic thunderstorms. Part II: Impact of radial velocity analysis via 3DVAR [J]. Mon. Wea. Rev., 134 (2): 699–721, doi:10.1175/MWR3093.1.
兰伟仁, 朱江, Xue M, 等. 2010. 风暴尺度天气下利用集合卡尔曼滤波模拟多普勒雷达资料同化试验I.——不考虑模式误差的情形 [J]. 大气科学, 34 (3): 640–652. Lan Weiren, Zhu Jiang, Xue M, et al. 2010. Storm-scale ensemble Kalman filter data assimilation experiments using simulated Doppler radar data. Part I: Perfect model tests [J]. Chinese J.ournal of Atmospheric Sciences (in Chinese), 34 (3): 640–652, doi:10.3878/j.issn.1006-9895.2010.03.15.
Li H, Kalnay E, Miyoshi T. 2009. Simultaneous estimation of covariance inflation and observation errors within an ensemble Kalman filter [J]. Quart. J. Roy. Meteor. Soc., 135 (639): 523–533, doi:10.1002/qj.371.
Miyoshi T. 2011. The Gaussian approach to adaptive covariance inflation and its implementation with the local ensemble transform Kalman filter [J]. Mon. Wea. Rev., 139 (5): 1519–1535, doi:10.1175/2010MWR3570.1.
Oye R, Mueller C, Smith S. 1995. Software for radar translation, visualization, editing, and interpolation [C]// Preprints, 27th Conference on Radar Meteorology. Vail, CO: American Meteorological Society, 359–361.
Putnam B J, Xue Ming, Jung Y, et al. 2014. The analysis and prediction of microphysical states and polarimetric radar variables in a mesoscale convective system using double-moment microphysics, multinetwork radar data, and the ensemble Kalman filter [J]. Mon. Wea. Rev., 142 (1): 141–162, doi:10.1175/MWR-D-13-00042.1.
秦琰琰, 龚建东, 李泽椿. 2012. 集合卡尔曼滤波同化多普勒雷达资料的观测系统模拟试验 [J]. 气象, 38 (5): 513–525. Qin Yanyan, Gong Jiandong, Li Zechun. 2012. Assimilation of Doppler radar observations with an Ensemble Kalman filter: OSS experiments [J]. Meteor. Mon. (in Chinese), 38 (5): 513–525.
Schumacher R S, Johnson R H. 2005. Organization and environmental properties of extreme-rain-producing mesoscale convective systems [J]. Mon. Wea. Rev, 133 (4): 961–976, doi:10.1175/MWR2899.1.
Snyder C, Zhang F Q. 2003. Assimilation of simulated Doppler radar observations with an ensemble Kalman filter [J]. Mon. Wea. Rev., 131(8): 1663–1677, doi:10.1175//2555.1.
Szunyogh I, Kostelich E J, Gyarmati G, et al. 2008. A local ensemble transform Kalman filter data assimilation system for the NCEP global model [J]. Tellus A, 60 (1): 113–130, doi:10.1111/j.1600-0870.2007. 00274.x.
Tong M J, Xue M. 2005. Ensemble Kalman filter assimilation of Doppler radar data with a compressible nonhydrostatic model: OSS experiments [J]. Mon. Wea. Rev., 133 (7): 1789–1807, doi:10.1175/MWR2898.1.
Torn R D, Hakim G J. 2008. Performance characteristics of a pseudo- operational ensemble Kalman filter [J]. Mon. Wea. Rev., 136 (10): 3947–3963, doi:10.1175/2008MWR2443.1.
Whitaker J S, Hamill T M. 2002. Ensemble data assimilation without perturbed observations [J]. Mon. Wea. Rev., 130 (7): 1913–1924, doi:10.1175/1520-0493(2002)130<1913:EDAWPO>2.0.CO;2.
Whitaker J S, Hamill T M, Wei X, et al. 2008. Ensemble data assimilation with the NCEP Global Forecast System [J]. Mon. Wea. Rev., 136 (2): 463–482, doi:10.1175/2007MWR2018.1.
许小永, 刘黎平, 郑国光. 2006. 集合卡尔曼滤波同化多普勒雷达资料的数值试验 [J]. 大气科学, 30 (4): 712–728. Xu Xiaoyong, Liu Liping, Zheng Guoguang. 2006. Numerical experiment of assimilation of Doppler radar data with an ensemble Kalman filter [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 30 (4): 712–728, doi:10.3878/ j.issn.1006-9895.2006.04.16.
Xue M, Tong M J, Droegemeier K K. 2006. An OSSE framework based on the ensemble square root Kalman filter for evaluating the impact of data from radar networks on thunderstorm analysis and forecasting [J]. J. Atmos. Oceanic Technol., 23 (1): 46–66, doi:10.1175/JTECH1835.1.
张进, 谈哲敏. 2008. 启动对流的初始扰动对热带飑线模拟的影响 [J]. 大气科学, 32 (2): 309–322. Zhang Jin, Tan Zhemin. 2008. Impacts of initial convection-triggering perturbations on numerical simulation of a tropical squall line [J]. Chinese Journal of Atmospheric Sciences (in Chinese), 32 (2): 309–322, doi:10.3878/j.issn.1006-9895.2008.02.10.
Zhang F, Snyder C, Rotunno R. 2003. Effects of moist convection on mesoscale predictability [J]. J. Atmos. Sci., 60 (9): 1173–1185, doi:10.1175/ 1520-0469(2003)060<1173:EOMCOM>2.0.CO;2.
Zhang F, Snyder C, Sun J Z. 2004. Impacts of initial estimate and observation availability on convective-scale data assimilation with an ensemble Kalman filter [J]. Mon. Wea. Rev., 132 (5): 1238–1253, doi:10.1175/1520-0493(2004)132<1238:IOIEAO>2.0.CO;2.
Impact of Bayesian Inflation Method on Assimilation of Doppler Radar Data with EnSRF Method
GAO Shibo1, 2, MIN Jinzhong1, 2, and HUANG Danlian1, 2
1,,2100442,,210044
The mesoscale convective system(MCS) occurred on 5 June 2009 in eastern China is simulated using the Advanced Regional Prediction System (ARPS) model and Doppler Radar data is assimilated with EnSRF. Bayesian inflation method is introduced in this study, which allows the inflation parameter to vary in space and time. The impact of Bayesian inflation method on assimilation of radar data with the ensemble square root filter (EnSRF) is investigated by comparing with the simulation using the multiplicative inflation method. Experimental results show that: the simulated composite reflectivity and cold pool from the Bayesian inflation experiment are stronger than that from the multiplicative inflation experiment; Bayes inflation method improves the performance of EnSRF, which always underestimates convection at the storm center. In the convective region, root mean square innovation of radial velocity and reflectivity in the Bayes inflation experiment are lower than that in the multiplicative inflation experiment. Further analysis indicates that the structure of Bayes inflation parameter corresponds very well to the root mean square innovation of reflectivity, which explains why the performance of EnSRF based on Bayes inflation method is improved. It is found that Bayes inflation method can give more weight to radar observations by increasing background error and provides bigger analysis increment when the root mean square innovation (RMSI) of background is bigger. Simulations of the two analysis fields show that the reflectivity near Hefei is stronger and the convective area of MCS is larger in Bayes inflation experiment than in the multiplicative inflation experiment. The simulated cold pool is colder and the area is bigger from Bayes inflation experiment than from the multiplicative inflation experiment, and corresponds well with observed reflectivity. ETS (Equitable Threat Score) of composite reflectivity from Bayes inflation experiment is higher than that from the multiplicative inflation experiment for various thresold. These resulsts suggest that Bayes inflation method improves the performance of EnSRF in radar data assimilation compared to that based on multiplicative inflation method.
EnSRF method, Radar data assimilation, Bayes inflation method, Multiplicative inflation method
1006-9895(2016)05-1033-15
P446
A
10.3878/j.issn.1006-9895.1511.15230
2015-07-12;网络预出版日期2015-12-01
高士博,男,1987年出生,博士研究生,主要从事雷达资料同化研究。E-mail: shibogao@126.com
闵锦忠,E-mail: minjz@nuist.edu.cn
国家重点基础研究发展计划(973计划)项目2013CB430102,江苏省普通高校研究生科研创新计划项目KYLX_0829、KYLX_0844,国家自然科学基金重点项目41430427,江苏省高校自然科学重大基础研究项目11KJA170001
Funded by National Basic Research Program of China (973 Program) (Grant 2013CB430102), the Research Innovation Program for College Graduates of Jiangsu Province (Grants KYLX_0829, KYLX_0844), National Natural Science Foundation of China (Grant 41430427), Key University Science Research Project of Jiangsu Province, the Priority Academic Program Development of Jiangsu Higher Education Institutions (Grant 11KJA170001)

