基于B-样条的波动方程数值解法

刘桂利



基于B-样条的波动方程数值解法

刘桂利

（哈尔滨金融学院 基础教研部，黑龙江 哈尔滨150036）

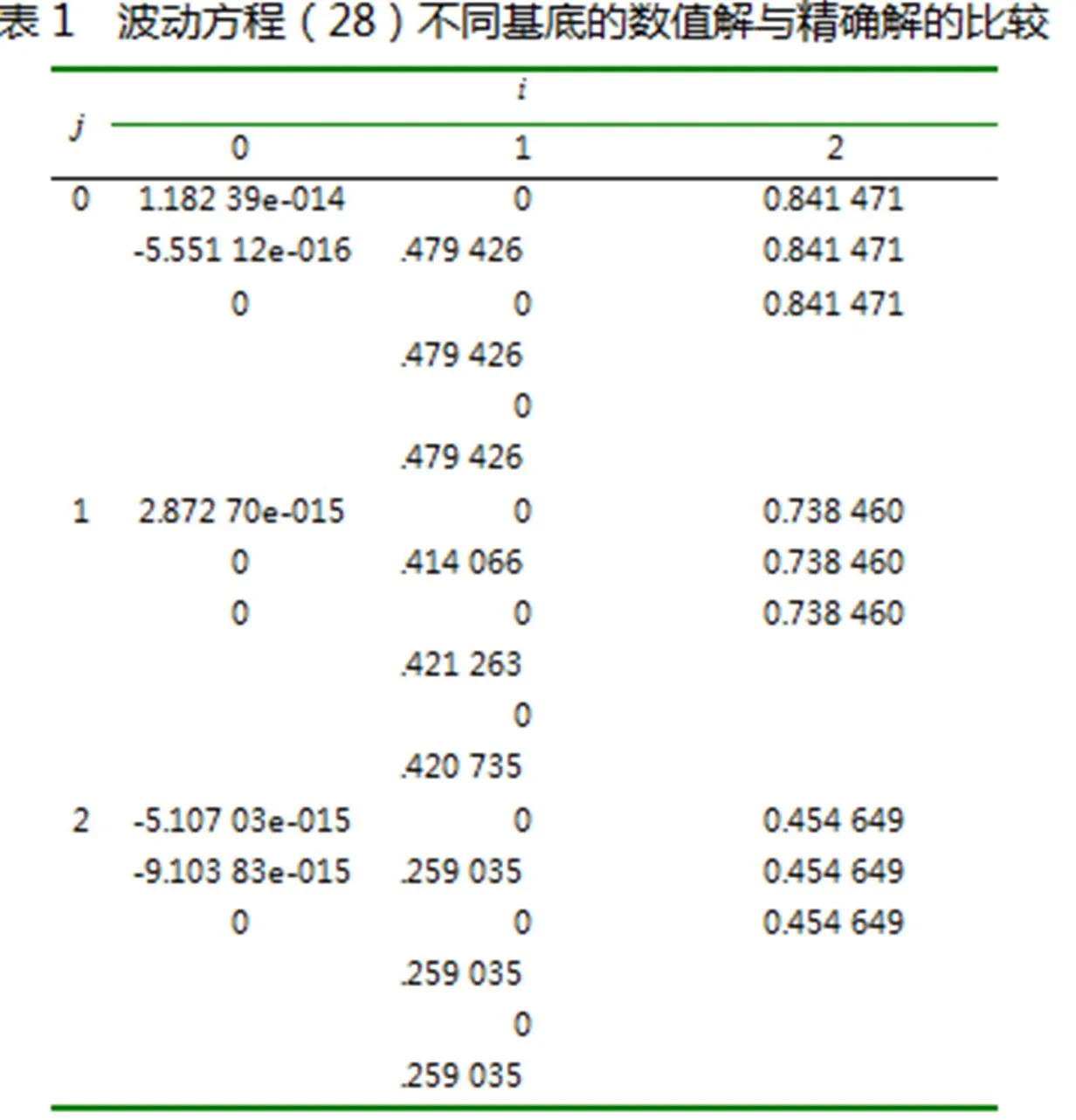
利用中的2组均匀B-样条和，给出波动方程的一种数值解法，并利用这2组B-样条所构造的拟插值算子讨论数值解的误差估计．得到为基底的数值解比以为基底的数值解要精确的结果．

B-样条；波动方程；拟插值算子；数值解

1问题的提出

求解如下波动方程边值问题

对矩型区域作均匀网格剖分[1-3]：，

2数值方法

由式（5）得

由式（6）得

由式（7）得

由式（8）得

由式（9）得

由式（10）得

由式（11）得

3数值算例

求波动方程边值问题

[1] 王仁宏．任意剖分下的多元样条分析（I）[J]．中国科学·数学专辑I，1979：215-226

[2] 王仁宏．任意剖分下的多元样条分析（II）——空间形式[J]．高等学校计算数学学报，1980（1）：78-81

[3] 王仁宏，施锡泉，罗钟铱，等．多元样条函数及其应用[M]．北京：科学出版社，1994

[4] 李崇君．特殊三角剖分上的多元样条及其应用[D]．大连：大连理工大学，2004

[5] Lai M J，Schumaker L L．On the approximation power of bivariate splines[J]．Adv Comput Math，1998（9）：251–279

[6] Boor C．B-form basics in Geometric Modeling：Algorithms and New Trends[M]．Philadelphia：SIAM，1987

[7] 廖肇源．样条函数在微分方程数值解中的若干应用[D]．大连：大连理工大学，2006

[8] Awanou G，Lai M J，Wenston P．The multivariate spline method for scattered data fitting and numerical solutions of partial differential equations in：Wavelets and Splines[M]．Brentwood：Nashboro Press，2006

The numerical method for solving the wave equation based on B-spline

LIU Gui-li

（Department of Basic Teaching and Research，Harbin Finance University，Harbin 150036，China）

Using the two groups ofanduniform B-spline in the，gave a kind of method of wave equation numerical solution，and used the quasi-interpolation operators of two groups of B-spline to discuss the error estimates of numerical solution．The numerical solution of based onis accurate than numerical solution of based on．

B-spline；wave equation；quasi-interpolation operator；numerical solution

O241.82

A

10.3969/j.issn.1007-9831.2016.03.006

2015-12-05

刘桂利（1978-），女，黑龙江虎林人，讲师，硕士，从事计算数学研究．E-mail：guili2005@126.com