中国股指现货和期货市场的日内波动与交易量:基于高频数据的证据
西村友作,孙便霞
中国股指现货和期货市场的日内波动与交易量:基于高频数据的证据
西村友作1,孙便霞2
(1.对外经济贸易大学国际经济研究院,北京100029;2. 南方科技大学金融数学与金融工程系,广东深圳518055)
随着金融高频交易的快速发展,日内金融资产价格的形成机制与市场微观结构发生了巨大变化。本文着眼于中国股票现货市场与期货市场的波动率和交易量的日内动态关系,基于沪深300股指现货与期货的5分钟数据,利用FFF回归与AR-FIEGARCH-V模型对日内波动率与交易量之间的动态关系进行了实证分析。本文的主要结论为:中国股票现货与期货市场的日内波动率,除了受到其本身的日内交易量的正向影响之外,还受到跨市场交易量的正向影响;同时,期货市场对现货市场的信息传导强度远大于现货市场对期货市场的信息传导强度,说明市场间的信息传导强度是不对称的。
股指期货;高频数据;日内周期性;FFF回归
0 引言
近年来,运用计算机分析股价、交易量等变量,几千分之一秒的时间瞬间完成金融交易的高频交易(high frequency trading)快速发展,日内股票价格的形成机制发生了巨大变化。在此背景下,金融市场的微观结构及市场间信息传播机制的研究显得越发重要。有鉴于此,本文从日内波动率与日内交易量的角度分析中国股票现货市场与期货市场的微观结构与信息传导机制。
金融资产波动率与交易量之间的关系一直是市场微观结构研究的重点。Karpoff[1]回顾了大量研究波动率与交易量关系的文献,并指出二者之间存在正相关关系。Lamoureux和Lastrapes[2]首次将GARCH模型应用于波动率与交易量关系的研究,针对纽约证券交易所上市的20只股票进行了实证分析,结果认为波动率显著受到交易量的正向影响①。此后,Najand和Yung[3]、Locke和Sayers[4]、Sharma等[5]等针对不同市场的不同金融资产应用各种研究模型进行了实证分析,对资产波动率与交易量存在正相关关系的结论基本上达到了共识。
国内许多学者针对股票市场(王燕辉和王凯涛[6];夏天2007[7];文凤华等[8][9]等②)和商品期货市场(华仁海和仲伟俊2003[10];徐剑刚和唐国兴[11];仲伟俊等[12])也对此问题进行了研究。国内几乎所有的文献都发现,与其他国家的金融市场类似,中国股票市场与商品期货市场的波动率也都受到交易量的正向影响。
以上相关文献的研究对象均为日波动率与日交易量③。随着中国金融市场上高频数据的使用成为可能,针对中国金融市场日内波动与日内交易量的研究也逐渐展开。马丹和尹优平[13]以2004年7月1日至9月31日的深发展的分笔数据为研究对象,运用超高频GARCH模型进行分析,发现股票价格波动率和成交量有正相关关系;刘向丽等[14]运用六个品种的商品期货从2007年4月27日到9月28日的1 分钟数据,利用Granger 因果检验方法,发现绝对收益率(波动率)与交易量之间存在双向的Granger 因果关系。张苏林[15]针对2010年4 月16日至2010年10月15日沪深300股指期货1分钟数据,使用EGARCH(exponential GARCH)模型发现,波动率显著受到预期交易量的负向影响,且受到非预期交易量的正向影响。
综合以上文献,本文发现现有的研究文献中仍然存在一些值得进一步深入的研究方向,主要为下述三个方面。首先,国内已有的研究主要是针对股票市场,部分是针对商品期货市场,即是以针对单一市场的研究为主的,而鲜有对现货与期货市场的运行特征及其微观结构的比较性研究与这些市场间的信息传播机制研究。其次,现有文献中金融资产波动与交易量的研究采用的大部分都是日度数据,忽略了日内时刻变动着的价格中包含的丰富信息,未能充分反映当前先进的通讯及交易技术环境下的微观结构。然后,Andersen和Bollerslev[16]、Andersen等[17]等大量研究发现,金融市场的日内波动蕴涵着日内周期性(intraday periodicity)、长记忆性(long-memory)等丰富的动态特征。因此,在针对日内高频数据建模时必须考虑到这些特征,否则得到的模型估计是有偏的(Andersen和Bollerslev,[16]),而现有的研究文献缺乏这方面的考虑。
基于以上认识,本研究的主要贡献体现在,首次对于2010年4月正式启动的股票指数期货市场与其现货市场的波动率与交易量的日内特征进行比较研究,并考察一个市场的交易情况对另一个市场波动状况的影响机制。具体而言,本文在Andersen和Bollerslev[16]中提出的FFF(Flexible Fourier Form)回归滤波的基础上,对日内高频收益率及其波动和日内交易量建立AR-FIEGARCH-V模型,并以此来分析日内波动率与日内交易量之间的动态相关关系。虽然股指期货是以股票现货价格指数作为标的物的衍生产品,但由于期货交易有逐日盯市和保证金制度,其市场微观结构特征也很可能不同于股票现货市场,本文的实证研究结果也验证了这一点。
本文后面的内容安排如下:第二部分对研究所用的日内高频数据及其日内周期性进行描述和分析,第三部分应用FFF回归滤波方法滤除日内波动率中的周期效应,日内波动与交易量的研究模型估计结果及分析在第四部分,第五部分则给出了本文的结论。
1 描述性统计与日内特征分析
1.1 数据概述
由于本文使用的是日内高频数据,因此首要的工作即为确定价格序列的采样频率。Aït-Sahalia等[18],以及Hansen和Lunde[19]等的大量研究表明,随着采样频率的提高,市场微观结构噪声所带来的问题会愈来愈严重。因此,必须在估计精度与噪声这两者之间进行权衡。Andersen等[20]和Koopman等[21]指出,5分钟价格序列可视为几乎不受到微观结构噪声影响的最高频率的数据。据此,本文亦采用时间间隔为5分钟的采样数据。
本文以沪深300股票指数和沪深300股指期货主力合约的高频价格序列与交易量序列作为研究对象,时间区间为股指期货正式上市交易的2010年4月16日至2012年2月13日,共442个交易日。国内现货市场的交易时间为北京时间上午9:30至11:30、下午13:00至15:00,共有48个日内观测点,因此在本文的研究时间段内沪深300股指现货5分钟价格数据与交易量数据各有21216个样本数据。国内期货的交易时间不同于现货市场,北京时间上午9:15至11:30、下午13:00至15:15,共有54个日内观测点,因此样本时间区间内沪深300股指现货5分钟价格数据与交易量数据各有23868个数据。本文的数据来源为飞狐数据库。
1.2 5分钟收益率序列与交易量序列的描述性统计量


表1 沪深300股指期货5分钟收益率序列的描述性统计量(%)
注:括号里的数字为标准误差;JB表示Jarque-Bera统计量;与分别表示日收益率序列与日收益率绝对值序列的滞后10期Ljung-Box统计量。
沪深300股指现货与期货的5分钟收益率的均值分别为0.0010与-0.0015,与其标准误差相比较可知,这些序列的均值均不显著异于零。现货与期货的5分钟收益率的偏度分别为0.3188与0.5935,其标准误差为0.0168与0.0159,在1%显著水平异于0,表明该序列的分布是右偏的。正的偏度意味着价格上涨时可能会出现极端值。从表中峰度可以看出,峰度在1%水平显著大于正态分布的3,说明沪深300股指现货与期货5分钟收益率的分布均具有厚尾特征。这意味着小概率事件发生的可能性大于正态分布。Jarque-Bera统计量显示,在1%的显著水平下拒绝服从正态分布的原假设,即收益率序列呈非正态分布。
1.3 波动率与交易量的日内动态特征
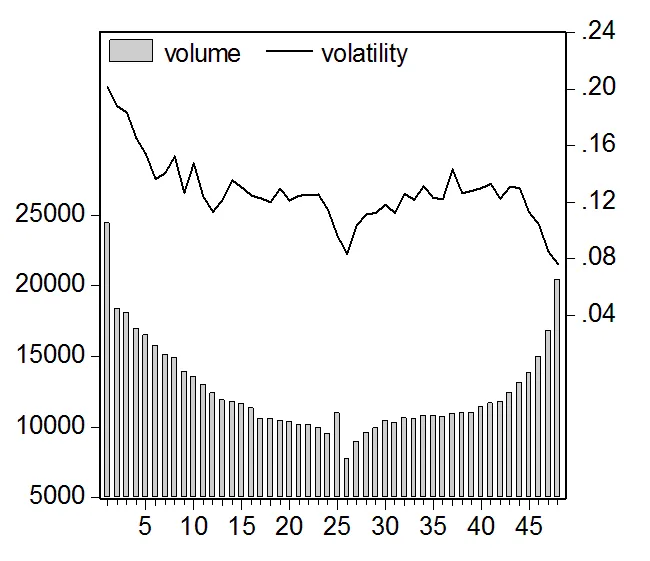
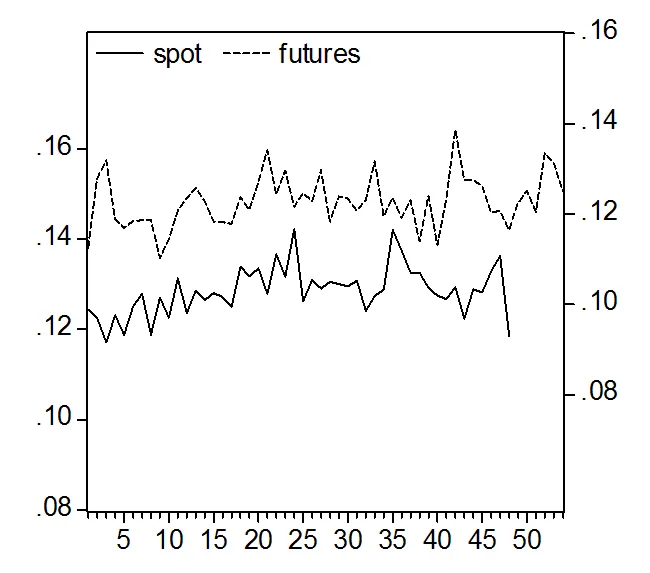
图1为沪深300股指现货(a)与期货(b)的5分钟平均波动率(把每天同一个时间点上的收益率的绝对值取其平均值)与5分钟平均交易量在一天交易时间内的走势图。
首先考察沪深300股指现货的情况。5分钟波动率序列在9:30开盘后达到整个交易日中的最高点。从上午开盘后,日内波动逐渐变小,并在午间休市前达到低位。午间休市结束,后市开市时日内波动又回到一个高位,且在后市交易时间内再次逐渐变小,直至全天休市时降至最低。交易量方面,沪深300股指现货的日内交易量呈现出明显的“U”型特征。中国股市在早上开盘之后的5分钟是交易最多的时间段,随后交易量逐渐下降直到前市收盘;而后市开盘后交易量又呈现逐步上涨趋势,且在后市收盘时交易非常活跃。显然,从图1中可以发现,波动率与交易量之间存在高度相关的动态模式,即交易量越多,股市波动越大。但值得关注的是,股市收盘前大约20分钟呈现不同动态特征,即随着交易量的增加5分钟波动率反而呈现出下降趋势。
(a)
(b)
图1 沪深300股指现货(a)与期货(b)的5分钟平均波动率与交易量的日内趋势图
注:实线表示日内波动率序列(右边刻度),棒状图表示日内交易量序列(左边刻度)。
下面考察沪深300股指期货的日内动态特征。从图1的右图中实线可以发现,沪深300股指期货的日内波动率大致呈现出“3V”(VVV)型特征。沪深300股指期货在9:15开盘后的波动率是整个交易时间中的最高点,随后波动率急剧下降,大致在股市现货市场开盘后的9:30-9:40时间段上波动率又开始变大;收益波动在前市收盘之前的11:25-11:30剧降到最低点。后市开盘后整个市场的波动率开始明显上升,在13:50-14:30之间维持较高波动;在现货股市波动率开始下降的14:40时股指期货市场的波动也开始急剧下降,进而在期货市场收盘前的15:10-15:15时间段内再次上升。这种期货日内波动率的变化趋势迥然不同于上述现货的情况。如果只看图1中期货市场与现货股市重叠交易的时间(9:30-15:00)段,则在这些时间段上沪深300股指期货的日内波动大致呈现出“M”型特征,这也不同于商品期货市场上的“L”型特征(刘向丽等[14])。值得一提的是,从图1的右图中可直观分析出,股指期货的日内波动率与日内交易量走势基本完全相吻合,即交易量增大时市场波动亦较大,而交易不活跃时市场波动也会比较小。
那么为什么沪深300股指现货的波动率与交易量在收盘前大约20分钟呈背离现象呢?比较图1中的两张图可以发现,后市波动率开始下降的时间均为14:40左右,而且该时间段正好是期货市场交易量大幅度下降的时候。由此本文认为,现货市场的波动率除了受本身的交易量影响之外,可能还受到期货市场上交易量的影响。对此问题,我们在第四节中将会进行详细的建模分析。
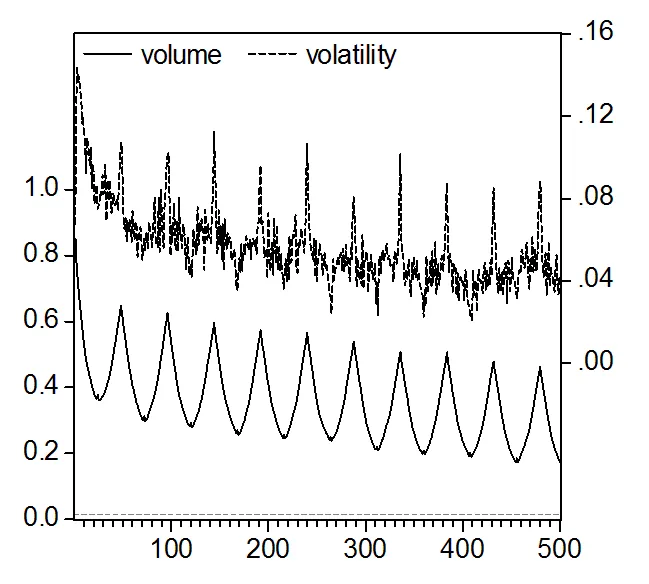
图2表示沪深300股指现货(a)与期货(b)的日内波动率序列与日内交易量序列在滞后1期至滞后10天(现货为480期,期货为540期)的自相关函数图。从这些图可以直观地看出,沪深300股指现货和期货的日内波动率与日内交易量的自相关函数存在极其明显的周期特征。且,自相关函数的这种动态特征基本上与图1中的日内走势相符合。
(a)
(b)
图2 沪深300股指现货(a)与期货(b)波动率与交易量的滞后10天的自相关函数
注:图中实线表示日内交易量序列(左边刻度),虚线表示日内波动率序列(右边刻度);横虚线表示5%临界值。
2 日内周期性的处理
在上面的分析当中,我们简单地将收益率的绝对值当做波动率进行了初步的分析。但这种方法计算出来的波动率并不精确,更常见的做法是应用(G)ARCH类模型来对波动率做更精确的估计。Andersen和Bollerslev[16]等许多相关文献指出,用高频数据计算的日内波动率具有周期动态特征,如果直接将日内高频数据应用于(G)ARCH类模型等经典的波动率模型中,其统计推论会产生偏误。因此,类似于对宏观经济序列建模时需进行季节调整,应用(G)ARCH类模型研究日内波动时,必须对剔除日内周期性之后的数据进行建模。为此,Andersen和Bollerslev[16]将Gallant[22]提出的FFF回归应用于金融高频数据的研究当中,并发现这种方法可以成功地剔除日内波动的周期性。下面对这一方法进行简单的介绍。
2.1 FFF回归方法
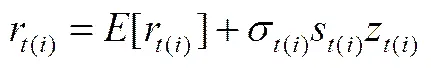
(3)
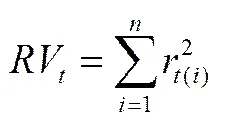
理论证明,只要日内收益率的抽样频率足够高,RV可视为真实波动率的一致估计量。
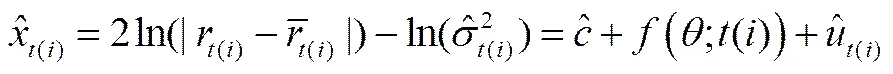
其中,
(6)
(a)
(b)
图3 滤波后日内收益率序列5分钟平均波动率及其自相关函数图
注:实线表示原序列(右边刻度),虚线表示滤波后的序列(左边刻度),横虚线表示5%临界值。
2.2 日内周期性的剔除
下面应用FFF回归从原始的沪深300股指现货和期货5分钟高频收益率序列中滤除日内周期性②,并对滤波后的数 据再次进行前述的平均波动率分析和自相关函数分析,具体 结果如图3所示。图3中的a图清晰地表明,两种指数滤波后的序列均围绕在其均值附近上下振荡,显示日内波动的周期性已被很好地剔除,且其自相关函数图也基本上不再存在周期循环(b图)。换言之,我们可以通过FFF回归刻画日内波动的动态特征,并利用这一方法来有效地剔除日内周期性。在下面的分析中,本文对滤波后的序列进行建模。另外,注意到图中的自相关函数呈现十分缓慢的衰减趋势,这意味着日内波动率具有很强的长记忆特征。
在交易量方面,由于本文使用的是交易量在每一时间段上相对前一时间段交易量的变化率,并不存在日内周期性问题,因此不需要对其进行类似上述方式的预处理。此外,与收益率序列的构造相类似,我们采用对数交易量的一阶差分来构造交易量5分钟变化率序列,且以百分数计。具体来说就是,即:
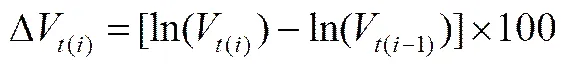
3 日内波动率与日内交易量关联性分析
在本节里,我们将日内波动率定义为可通过(G)ARCH类模型得到的条件异方差,并分析日内交易量的变化对波动率的影响。本节的实证分析主要试图回答下面两个方面的问题:第一,沪深300股指现货或期货的日内波动率是否受到本市场交易量的影响?第二,一个市场的日内波动率是否受到另一市场日内交易量的影响?
3.1 日内交易量对市场内日内波动率的影响
3.1.1 分析方法
一般的(G)ARCH类模型需要加以非负约束,以保证条件方差为正。由于日内交易量的变化率有正有负,因此不适合在常规的(G)ARCH类模型中作为外生的解释变量来引入。Nelson (1991)[24]提出的EGARCH(exponential GARCH)模型中,方差采用的是对数形式,同样可为正值或负值,因此这里我们可采用EGARCH模型来进行建模研究。另外,虽然我们应用FFF回归解决了日内周期性问题,但日内波动中仍然存在着明显的长记忆性特征。有鉴于此,本文采用Bollerslev和Mikkelsen(1996)[25]提出的能够刻画波动长记忆性的FIEGARCH(fractionally integrated EGARCH)模型。
具体地,我们将日内交易量的变化率引入到FIEGARCH模型的方差方程中,建立市场的AR()-FIEGARCH(1,,0)-V模型,即:

,(8)
(9)
这里,式(8)为均值方程,用AR()模型来表示;式(9)为方差方程,用FIEGARCH(1,,0)模型来表示;为服从标准正态分布的白噪声序列。
3.1.2 检验结果
AR-FIEGARCH-V模型的极大似然估计结果,如表2所示①。我们最关注的是参数的估计结果。对股指现货数据和期货数据分别建立的模型中,参数的估计值分别为0.0213与0.0170,且均在1%的水平下显著。这意味着,无论是沪深300股指现货市场还是期货市场,日内交易量对日内波动率都具有正向的影响。这基本符合已有的相关文献中对日度波动率和交易量的研究结果,显然,中国金融市场上的日内波动率,与日度波动率一样,同样受到市场交易量的正向影响。

表2 模型主要参数的估计结果
注:***和**分别表示在1%和5%水平显著;括号中的数字为估计系数的标准误差;表示对数似然值;表示标准化残差平方序列的Ljung-Box统计量。表中省略了AR模型估计结果。
另外,大量相关研究发现,金融资产日收益率一般具有波动非对称特征,而且利空消息对波动率的影响大于利好消息的影响(例如Xekalaki and Deiannakis[26]等)。本文模型中的参数可以用于判断日内情况下是否也存在市场的非对称影响。此处参数均在1%水平下显著为负,表明沪深300股指现货与期货的5分钟收益率也有波动非对称性特征,而且同等强度的利空消息比利好消息对波动性的影响程度更大。显然,该结果与使用日度收益率的研究结果相一致。
进一步地,对加入交易量的AR-FIEGARCH-V模型与不加入的AR-FIEGARCH模型进行比较可以发现,波动持续性参数有显著性下降,即现货模型从0.7634下降到0.5369,期货模型从0.6452下降到0.1121。该结果与华仁海和仲伟俊(2003)[10]、王燕辉和王凯(2004)[6]、夏天(2007)[7]等许多针对中国金融资产的相关研究是相一致的。这种现象可用Clark(1973)[27]提出的混合分布假说(mixture distribution hypothesis)来解释。该假说认为,收益率的方差(波动率)是流向市场的信息量的函数,因此新信息的不断流入将会直接影响资产收益的波动率。换言之,信息变量的引入在一定程度上替代了波动率的历史对其自身的解释能力,进而降低了波动率模型中的持续性参数。从混合分布假说的角度来看,沪深300股指现货与期货的交易量也可视为度量各自市场上信息流量的代理变量。
最后,我们对上述模型中得到的标准化残差的平方序列进行了Ljung-Box检验。结果显示,虽然期货模型的残差平方序列不存在自相关,然而现货模型拒绝了不存在序列自相关的原假设。这表明现货模型的设定可能存在一些问题,尚有待改善。
3.2 日内交易量对跨市场日内波动率的影响
3.2.1 分析方法
在上节中,我们发现一个市场的日内波动率确实受到其自身的日内交易量的正向影响,下面我们来回答第二个问题,即期货(现货)市场的日内交易量是否会影响现货(期货)市场的日内波动率。在上节对市场进行AR-FIEGARCH-V建模的基础上,将市场的日内交易量变化率引入到模型的方差方程中,检验市场的日内交易量对市场的日内波动率的影响,即:

,(10)
(11)
值得说明的是,因为沪深300股指现货与期货的交易时间长度不同,因此本文删除了两个市场上交易时间不重叠时的交易数据,最终得到的样本总数为20774个。
3.2.2 检验结果
对沪深300股指现货和期货数据分别建立模型(10)(11),表3给出的是模型(11)的参数极大似然估计结果。这里我们最关注的是参数,它能够反映日内交易量的跨市场影响效应。在股指现货模型中,参数的估计值为0.0111,在1%的水平下显著,且其大小与参数基本相同。这表明沪深300股指现货的日内波动率,除了受其本身的交易量正向影响之外,还受到股指期货交易量的正向影响,且二者的影响幅度基本相同。

表3 跨市场AR-FIEGARCH-V模型主要参数的估计结果
注:***和**分别表示在1%和5%水平显著;括号中的数字为估计系数的标准误差;表示对数似然值;表示标准化残差平方序列的Ljung-Box统计量。表中省略了AR模型估计结果。
最后我们对标准化残差的平方序列进行Ljung-Box检验,以检查模型的设定情况。结果显示,两种模型均不能拒绝不存在序列相关的原假设,说明将期货市场交易量作为外生变量加入到现货模型中,有效改善了模型对日内波动率的刻画能力。由此可以推断,本文建立的跨市场AR-FIAPARCH-V模型是合适的。
4 结束语
本文主要着眼于中国股票现货市场与期货市场的日内波动率与日内交易量之间的动态关系,基于沪深300股指现货与期货的的5分钟高频数据,运用FFF回归与AR-FIEGARCH-V模型对波动率与交易量之间的动态关系进行了实证分析。本文的主要结论如下:
(1)与已有的相关文献中针对日度数据的研究结果相一致,沪深300现货市场与期货市场的日内波动率与日内交易量之间同样存在着正相关关系。同时,将交易量作为外生变量引入到波动率模型中后,波动模型中的持续参数明显变小,印证了Clark(1973)[27]的混合分布假说。
(2)沪深300股指现货与期货的日内波动率,除了受其自身交易量的正向影响之外,还受到跨市场交易量的正向影响。但这种信息传导强度是不对称的,即期货市场对现货市场的信息传导强度,远大于现货市场对期货市场的信息传导强度。我国股指期货市场对投资者有门槛限制,能参与股指期货交易的投资者必定也能参与股票交易,反之则不一定,这也是股指期货市场在现货-期货信息传导机制中居于主导地位的原因之一。
本文重点研究了中国股市现货市场与期货市场的日内波动率与日内交易量之间的关系,并没有讨论收益率与交易量之间的关系以及现货市场与期货市场的波动率之间和交易量之间的关系。显然,这些都是进一步深入研究中国金融市场微观结构的可行方向。另外,理论上而言,期货价格相当于现货价格与利息之和,当前者背离后者时,套利机会就会出现。而有效市场理论认为,与市场有关的所有信息都会反映到价格上来,因而在有效的市场上这种套利交易策略的交易机会是稍纵即逝的。因此,通过对现货与期货之间的价差进行研究,可以检验市场的有效性。显然,未来这种基于高频数据的市场有效性研究也是一个具有重要意义的研究方向。
[1] Karpoff J.M. The Relation between Price Changes and Trading Volume: A Survey [J].Journal of. Financial and Quantitative Analysis, 1987, 22(1):109-126.
[2] Lamoureux C.G., Lastrapes W.D.Heteroskedasticity in Stock Return Data: Volume versus GARCH Effects [J]. Journalof Finance, 1990, 45(1):221-229.
[3] Najand M. Yung K.A. GARCH Examination of Relationship between Volume and Price Variability in Futures Markets [J]. Journal ofFutures Markets, 1991, 11(5):613-621.
[4] Locke P.R. Sayers C.L. Intra-day Future Price Volatility: Information Effects and Variance Persistence [J]. Journal of Applied Econometrics, 1993, 8(1):15-30.
[5] Sharma J.L., Mougoue M., Kamath R. Heteroscedasticity in Stock Market Indicator Return Data: Volume versus GARCH Effects [J]. Applied Financial Economics, 1996, 6(4):337-342.
[6] 王燕辉,王凯涛.股票交易量对收益率波动性的影响---对深市个股的实证分析[J].金融研究,2004,12:81-88.
[7] 夏天.基于CARR模型的交易量与股价波动性动态关系的研究[J].数理统计与管理,2007,26(5):887-895.
[8] 文凤华,饶贵添,张小勇,杨晓光.去异方差交易量与价格波动关系研究[J].管理科学学报,2010,13(3):64-72.
[9] 文凤华,刘晓群,唐海如,杨晓光.基于LHAR-RV-V模型的中国股市波动性研究[J].管理科学学报,2012,15(6):59-67.
[10] 华仁海,仲伟俊.我国期货市场期货价格收益、交易量、波动性关系的动态分析[J].统计研究,2003,7:25-30.
[11] 徐剑刚,唐国兴.期货波动与交易量和市场深度关系的实证研究[J].管理科学学报,2006,9(2):69-75.
[12] 仲伟俊,刘庆富,梅妹娥.中国期市波动性与收益率、交易量和空盘量的关系[J].系统工程学报,2008,23(4):508-512.
[13] 马丹,尹优平.交易间隔、波动性和微观市场结构---对中国证券市场交易间隔信息传导的实证分析[J].金融研究,2007,7:165-174.
[14] 刘向丽,程刚,成思危,汪寿阳,洪永淼.中国期货市场日内效应分析[J].系统工程理论与实践,2008,8:63-80.
[15] 张苏林.交易量和波动率动态因果关系研究---基于沪深300股指期货高频数据的实证分析[J].金融理论与实践,2008,3:92-96.
[16] Andersen T.G., Bollerslev T. Intraday Periodicity and Volatility Persistence in Financial Markets [J].Journal of Empirical Finance, 1997, (4):115-158.
[17] Andersen T.G., Bollerslev T, Cai J. Intraday and Interday Volatility in the Japanese Stock Market [J].Journal of International Financial Markets, Institutions and Money, 2000, 10:107-130.
[18] Aït-Sahalia Y., Mykland P.A., Zhang L. How Often to Sample a Continuous-TimeProcess in the Presence of Market Microstructure Noise [J]. Review of Financial Studies,2005, 18(2): 351-416.
[19] HansenP.R., Lunde A. Realized Variance and Market Microstructure Noise [J]. Journal of Business and EconomicStatistics, 2006, 24: 127-161.
[20] Andersen T.G., Bollerslev T., Diebold F.X, Ebens H. The Distribution of RealizedStock Return Volatility [J]. Journal of Financial Economics,2001, 61(1):43-76.
[21] Koopman S.J., Jungbacker B., Hol E. Forecasting Daily Variability of the S&P 100 Stock Index Using Historical Realised and Implied Volatility Measurements [J] Journal of Empirical Finance, 2005, 12(3):445-475.
[22] Gallant A.R. On the Bias in Flexible Functional Forms and an Essentially Unbiased Form: The Fourier Flexible Form [J].Journal of Econometrics, 1981, 15:211-245.
[23] Andersen T.G., Bollerslev T. Answering the Skeptics: Yes, Standard Volatility Models Do Provide Accurate Forecasts [J].International Economic Review, 1998, 39:885-905.
[24] Nelson, D.B. Conditional Heteroskedasticity in Asset Returns: A New Approach [J]. Econometrica, 1991, 59(2):347-370.
[25] Bollerslev T., Mikkelsen H.O. Modeling and Pricing Long Memory in Stock Market Volatility [J]. Journal of Econometrics, 1996, 73(1):151-184.
[26] Xekalaki E., Degiannakis S. ARCH Models for Financial Applications [M]. 2010, New York: John Wiley & Sons.
[27] Clark, P.K. A Subordinated Stochastic Process Model with Finite Variance for Speculative Prices [J]. Econometrica, 1973, 41(1):135-155.
Intraday Volatility and Volume in Chinese Stock Index Cash and Futures Markets: Evidence from High Frequency Data
NISHIMURA Yusaku1, SUN Bian-xia2
(1. University of International Business and Economics, Beijing 100029, China; 2. South University of Science and Technology of China, Shenzhen 518055, China)
Along with the rapid development of high frequency trading in financial markets, asset price forming mechanism and market microstructures have changed greatly. Thus, the study on information transmitting mechanism between financial markets becomes more important. Price movements and volume changes reflect information flow in financial markets. Targeting the CSI 300 Index and Index Futures markets, this paper studies information transmitting mechanisms between Chinese stock index cash and futures markets. The data sample ranges from Apr 16, 2010 to Feb 13, 2012, covering 442 trading days in total.
Much present research has displayed periodic characteristics among intraday financial volatility. This periodicity must be taken into account when modeling intraday volatility. The descriptive analysis based on 5-min interval data reveals a U shape for intraday volatility of the stock index cash market, and a 3V (or VVV) shape for that of the corresponding futures market. According to Andersen and Bollerslev (1997), we use the FFF regression method to preprocess high frequency return series to remove the intraday volatility periodicity.
This paper attempts to answer two questions. First question is whether the intraday volatility of CSI 300 Index cash (futures) markets is influenced by internal intraday trading volume. Second question is whether intraday volatility in one market is influenced by external trading volume in the other market. Considering long memory characteristic of intraday volatility series, this paper adopts the FIEGARCH model (Bollerslev and Mikkelsen, 1996) and introduces intraday volume change into the variance equation of the research model. Consequently, the AR-FIEGARCH-V model is built to study the influence of intraday trading volume on intraday volatility in (between) Chinese stock index cash and futures markets.
Empirical study shows that intraday trading volume positively influences the volatility of the same market, which is in accord with the results of much present work using daily data. Our study also finds that the volume of the index futures (cash) market has positive influence on intraday volatility of stock index cash (futures) market. In addition, the influential power of futures market on cash market is relatively much stronger. This denotes an asymmetric bidirectional information transmitting mechanism between Chinese stock index cash and futures markets. The information flow from futures market to cash market is stronger than the opposite situation. In China only investors satisfying some requirements can trade in the stock index futures market, quite different from the stock market without such limits, which may contribute to asymmetric information transmission between stock index cash and futures markets in China.
stock index futures; high frequency data; intraday volatility periodicity; FFF regression
中文编辑:杜 健;英文编辑:Charlie C. Chen
F830
A
1004-6062(2016)02-0093-08
10.13587/j.cnki.jieem.2016.02.011
2013-09-12
2014-01-05
国家博士后科学基金资助面上项目(2013M530167)
西村友作(1974-),男,日本熊本人,对外经济贸易大学国际经济研究院副教授,博士,研究方向:金融市场与金融风险管理。
①Lamoureux和Lastrapes(1990)[2]将交易量作为外生变量加入到GARCH模型中,实证结果显示:第一,波动率显著受到交易量的正向影响;第二,波动持续性变小,进而GARCH模型中的ARCH项与GARCH项的显著性下降;第三,加入交易量之后,GARCH模型的标准化残差服从正态分布。
②文凤华等(2010)[8]除了中国国内股市之外,还研究了法国CAC 40指数、德国DAX指数、日本日经225指数、美国S&P500指数、瑞士SWISS市场指数、新加坡的STI指数等其他主要国家的情况。结果发现这些所有股票市场都能观测到波动率与交易量的正相关关系。
③虽然文凤华等(2012)[9]使用了沪深300 指数的1分钟数据,但用它来计算日度的已实现波动率(RV)后建立LHAR-RV-V模型分析了日RV与日交易量之间的相关关系。
① FFF回归的详细内容参见Andersen和Bollerslev(1997)[16]Appendix B pp.152-155等。
①关于AR()模型滞后期,本文根据AIC准则确定最有滞后期。具体而言,滞后期在第0~30期中选择使得AIC最小的滞后期,最终选择了AR(7)模型。由于均值方程并不是本文的讨论重点,而且估计结果极为冗长,考虑到篇幅的关系,表2中省略了AR模型的具体估计结果。

