基于随机调频步进信号的高分辨ISAR成像方法

吕明久 李少东 杨 军 马晓岩



基于随机调频步进信号的高分辨ISAR成像方法

吕明久*李少东 杨 军 马晓岩

(空军预警学院 武汉 430019)

为充分利用随机调频步进逆合成孔径雷达回波所具有的联合稀疏特征，提高成像性能，该文提出一种基于分布式压缩感知理论的随机调频步进逆合成孔径雷达高分辨成像方法。首先构建随机调频步进信号回波的联合稀疏表示模型，并完成子脉冲的脉冲压缩处理；其次，基于每组子脉冲的随机方式(组与组之间的随机方式不同)，构建相应的随机量测矩阵，获取回波的压缩感知信号模型，并利用分布式压缩感知理论实现距离向联合高分辨重构；最后结合回波在方位向的稀疏性，采用快速稀疏重构算法实现方位向高分辨成像。理论分析和仿真结果表明由于充分利用了随机调频步进信号回波的随机性与联合稀疏特征，所提出方法具有重构精度高、距离向采样率低、抗噪性能强等特点。

逆合成孔径雷达成像；联合稀疏模型；分布式压缩感知；随机调频步进信号

1 引言

根据逆合成孔径雷达(Inverse SAR, ISAR)成像原理，距离分辨率由发射信号的带宽决定。带宽的增加可提高距离分辨率，但受香农采样定理的限制，增加带宽将面临接收机采样率过高、数据量过大及传输处理困难等问题的挑战。近年来，众多学者充分利用目标分布的稀疏特征，将压缩感知(Compressed Sensing, CS)[1]理论应用到ISAR成像中，在显著降低数据量的同时提高了成像质量。然而由于缺乏实际的压缩采样硬件设备，目前基于CS的传统线性调频ISAR(Linear Frequency Modulation ISAR, LFM ISAR)在成像时，大都对按照Nyquist采样获得的数据进行人为的随机抽取来“等效”随机降采样的过程，因此并没有真正意义上减小成像所需数据量、降低对雷达接收机处理能力的要求[4,5]。

为缓解ISAR成像接收机处理难度，文献[6,7]提出一种低复杂度的压缩宽带雷达感知系统，其结构是发射机发射的是多频段的chirp信号波形，而接收机则利用一个模拟混频器后接一个欠采样器来实现。降低了接收端对采样率的要求，具有系统复杂度低、抗干扰能力强、易于工程实现等优点。实际上，文献[11-13]所涉及的随机调频步进(Random Chirp Frequency-Stepped, RCFS)波形都可认为是将CS的随机性由接收端“转移”到发射端从而降低了硬件设计复杂度。对于随机调频步进ISAR(RCFS ISAR)成像系统，目前大都基于单量测向量(Single Measurement Vectors, SMV)模型进行处理，并没有进一步考虑目标的物理结构稀疏特征，因而处理效率较低且抗噪声性能较差[14,15]。文献[16]基于多量测向量(Multiple Measurement Vectors, MMV)模型对稀疏调频步进信号进行联合稀疏重构，提高了重构效率和抗噪性能。但是该发射波形要求每组脉冲信号随机方式相同，并没有真正实现发射波形的全随机。因此，研究这种发射全随机的RCFS波形处理方法，进一步提高RCFS-ISAR成像性能具有十分重要的意义。

为充分利用CS理论在降低数据量、提高分辨率等方面的优势以及目标分布的结构稀疏特征，该文提出一种基于分布式压缩感知[17](Distributed Compressed Sensing, DCS)的RCFS ISAR高分辨成像方法。分布式压缩感知理论主要通过利用回波信号联合稀疏特征，将单个信号重构问题扩展为多个信号同时重构的问题，具有量测数更少、重构误差更低和抗噪性能更强的优势[18]。在成像过程中，由于每组RCFS回波都经由具有同一物理特性的目标反射，所有回波具有相同的稀疏结构，可以基于DCS理论进行距离向高分辨重构。因此，文中在完成子脉冲回波压缩后，首先得到RCFS ISAR联合稀疏回波模型，针对每组子脉冲随机方式的不同设计不同的量测矩阵，并利用回波信号联合稀疏的特性，基于DCS理论实现RCFS的“二次脉冲压缩”处理，得到距离向的高分辨联合重构结果。在方位向采用快速的稀疏重构算法实现高分辨的方位成像，最终实现2维高分辨ISAR成像。理论分析和仿真结果表明该方法具有距离向采样率低、重构精度高、抗噪性能强的优势。

2 RCFS ISAR稀疏回波模型

传统均匀调频步进(Chirp Frequency-Stepped, CFS)信号，其第组第个子脉冲回波信号可表示为[12]

RCFS信号可以看作为传统CFS信号的随机降采样形式，即对式(1)中距离向完整的个子脉冲随机抽取个子脉冲进行发射，则RCFS雷达信号第组第个子脉冲回波可表示为

为[12]

(4)

对于式(3)还需进行“二次脉冲压缩”才能完成距离像合成[13]。对于上述回波模型，由于随机选择方式不同，因此每个脉组中随机发射的子脉冲不尽相同。当利用CS进行距离向“二次脉冲压缩”重构时需根据每组子脉冲随机方式设计不同的量测矩阵，只能利用传统SMV模型对各列数据分别进行重构。下面通过对每组子脉冲之间联合信息的挖掘，研究基于DCS理论的RCFS ISAR成像方法。由于主要分析的是组回波信号之间的联系，为叙述简便，因此将简写为，且记。

3 基于DCS的RCFS ISAR成像方法

由电磁探测理论可知[19]，对于雷达发射的不同电磁脉冲信号，不管信号形式如何，回波信号目标的信息主要体现在幅度和相位上。由于目标的空间分布相对于观测区域是稀疏的。因此，经由同一个目标反射的回波信号具有相同的稀疏结构，也即用于方位向组回波采样信号在同一稀疏基下具有相同的稀疏结构，只是在雷达成像过程中，由于观测角度、环境的影响，使得幅度、相位信息可能有所差异，这种信号模型通常被称之为联合稀疏模型[17]，具体结构如图1所示。

图1 联合稀疏模型

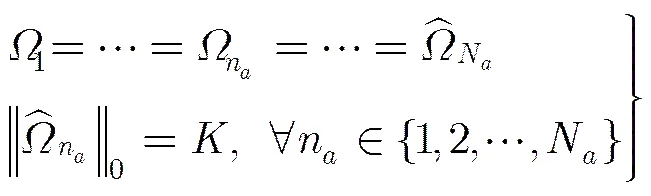
传统CS稀疏重构算法在处理这类问题时，可以基于最小0-范数对每个回波信号分别进行重构，具体过程如式(7)所示[1]。

(8)

图2 基于联合稀疏模型的重构示意图

利用式(8)进行重构时，每个信号在重构时的量测矩阵都不相同，但是所有信号共享支撑集信息。分布式压缩感知利用信号联合稀疏这一特点，在重构每个稀疏信号时利用所有信号支撑集相同这一先验信息，提高了重构性能。目前，已经提出了多种分布式压缩感知稀疏重构算法[18,20]，本文利用DCS- SOMP算法实现距离向的联合重构。该算法主要是基于OMP算法进行的改进，在求取支撑集时利用了信号联合稀疏的特性，使之适用于联合稀疏模型的信号重构，算法具体实现过程可参考文献[20]。通过上述分布式压缩感知稀疏重构算法处理后即可完成组距离像的高分辨重构。

(10)

对于方位向成像，利用方位向的稀疏性，通过CS理论同样可以实现方位向的稀疏重构。具体过程为

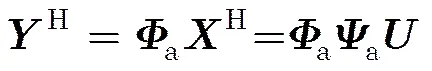
为提高方位向分辨率，可按照距离向稀疏基设计方法得到方位向稀疏基。理论上，方位向分辨率为，将目标区域沿方位向进行离散化得到，散射点所占的多普勒频点在整个多普勒域同样是稀疏的，因此根据式(3)可构造出方位向高分辨稀疏基：

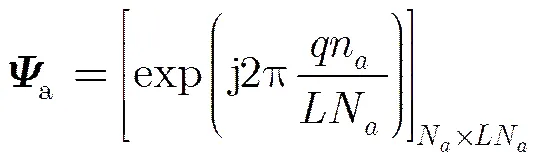
“互联网+”是社会热潮，也是国家战略部署。高校是重要的创新创业教育的实施主体，而高师院校应注重创新创业意识的培育而非实践。通过对我国高师院校创新创业教育现状的分析，结合互联网的特点，探索培育学前教育师范生创新创业意识的途径，建立和培养一支强有力的创新型教师队伍，为我国高师院校创新创业教育助力，为师范生自身发展与幼儿创新思维的培育助力。

4 成像性能理论分析

4.1 距离向采样率分析

对于一个稀疏信号，传统单量测向量模型条件下基于CS进行准确重构的条件为[21]：。而对于联合稀疏条件下的重构模型，文献[22]指出得到联合稀疏信号唯一解的充要条件为

4.2 抗噪性能分析

一般情况下，接收到的信号都会伴随着噪声，更精确的回波量测模型为

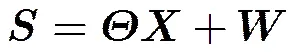
(15)

由于噪声的存在，传统OMP算法在求取内积时，弱散射点位置有可能被噪声所淹没，使得位置估计不准。假设经过第次迭代的残差信号为，此时由于噪声的存在，使得残差信号不仅含有原始信号部分，而且包含噪声信号。将分解为无噪分量与噪声分量两部分得到：。此时求取内积为

5 仿真验证与分析

首先给出本文的噪声添加方式以及成像质量评价指标。文中噪声添加方式同文献[4]。采用重构精度与支撑集匹配度作为距离像重构性能评价指标。距离像重构精度计算公式为。式中为原始信号，为重构的信号。距离像支撑集匹配度计算公式为。式中为信号支撑集；为估计的信号支撑集；代表集合的势；为期望。当匹配度值越大时，说明对支撑集的估计精度越高。对于最终成像质量采用图像熵以及目标背景比(Target-to-Background Ratio, TBR)[23]作为衡量指标。

图3 RCFS ISAR成像处理流程图

另外，需要指出的是仿真中方位向成像均采用MSL0算法进行重构，传统方法距离向处理采用的为OMP算法，本文方法距离向处理采用DCS-SOMP算法。仿真所用RCFS信号载频，频率步进量，脉宽，子脉冲个数，脉组数，参考距离。

5.1 距离像重构性能仿真分析

仿真1 距离向采样率与重构误差仿真分析 为分析方便，此处不失一般性假设3点散射点模型用于研究本文方法与传统CS方法在重构距离像时的性能差异。图4为本文算法与传统算法在不同采样率条件下距离像重构结果，信噪比设置为30 dB。

图4(a)中，采样率为0.1时，传统OMP算法重构结果中只有1个散射点的位置重构正确。而DCS- SOMP算法可以正确重构出全部3个散射点的位置。图4(b)中，采样率提高为0.3时传统OMP算法、DCS- SOMP算法都能正确搜索到散射点位置，但是DCS- SOMP算法重构出的散射点幅度更接近于真实值，精度更高，显示出基于联合稀疏模型的DCS-SOMP算法良好的重构性能。

仿真2 抗噪性能仿真分析 为检验本文方法的抗噪性能，假设3点散射点模型强度分别为，图5为不同信噪比条件下的本文算法与传统算法距离像重构结果示意图。

图5(a)中，当信噪比为25 dB时，传统OMP算法不能重构出幅度为0.1的散射点。而DCS-SOMP算法可以准确重构出弱小散射点。图5(b)中，当信噪比为5 dB时，OMP算法无法重构出弱散射点的位置。DCS-SOMP算法在信号数为16的条件下同样无法重构出弱散射点的位置。当信号数为128时，DCS- SOMP算法已经可以成功地重构出弱散射点。上述实验也验证了基于联合稀疏模型的DCS-SOMP算法可以提高对弱散射点的检测能力，因此具有良好的抗噪性能。

5.2 ISAR成像性能仿真分析

下面研究基于DCS的RCFS ISAR成像性能。采用文献[24]中的Mig25回波数据验证本文方法的有效性。该数据事先已经完成运动补偿，其主要参数为载频，重复频率，子脉冲个数，脉组数。为模拟信号的随机性，对子脉冲信号进行随机选择，且每个脉组的随机选择方式不同，方位向选取前64个脉组数据参与处理。

仿真3 不同距离向采样率条件下成像性能仿真 在不同的距离向采样率条件下得到的目标2维成像结果如图6所示。

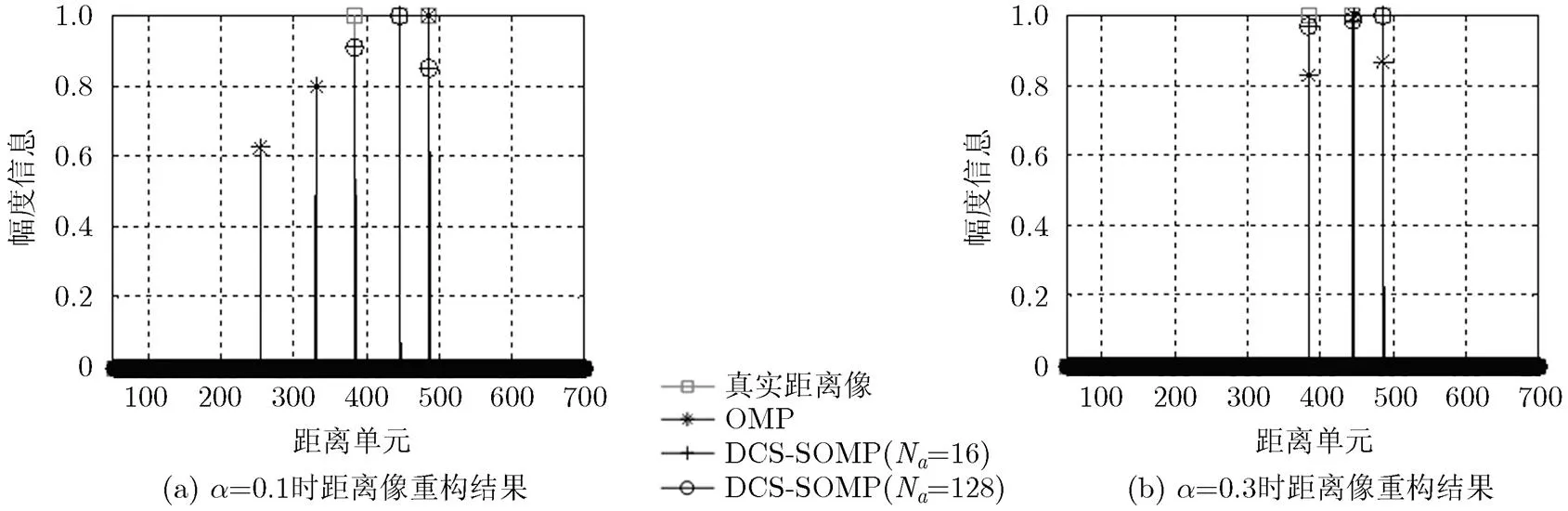
图4 不同采样率条件下距离像重构结果示意图

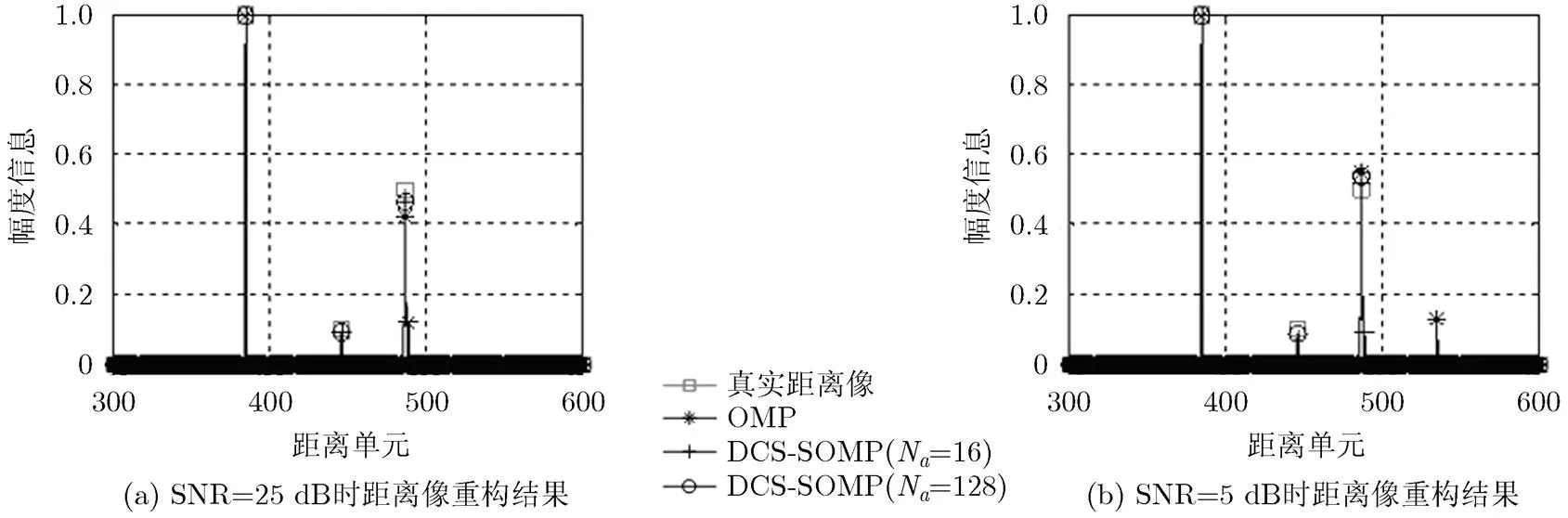
图5 不同信噪比条件下距离像重构结果示意图

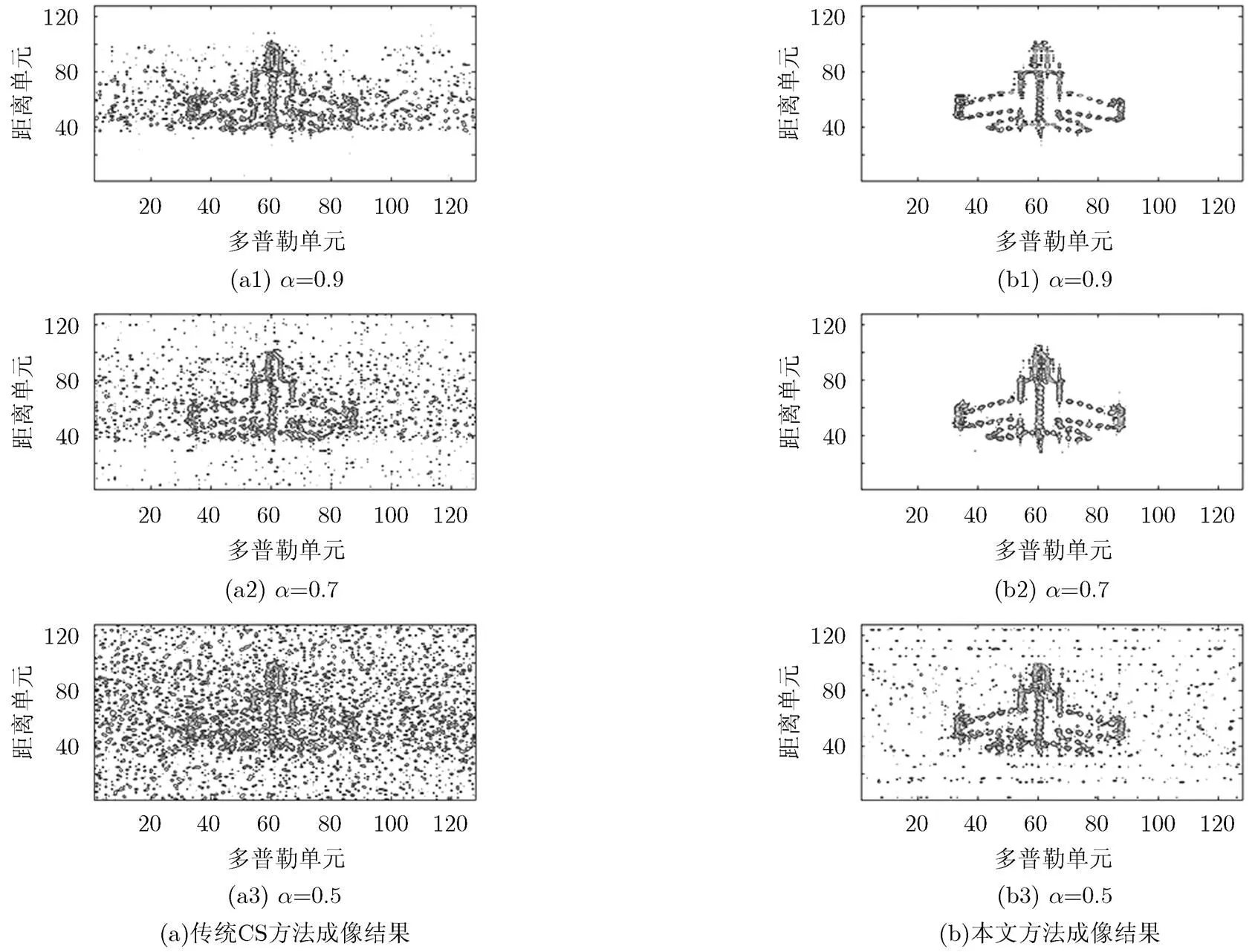
图6 不同采样率条件下目标2维成像结果

图6(a)中，传统CS方法得到的成像结果存在较多虚假重构点，而图6(b)的成像结果虚假重构点较少。当采样率将至0.5时，传统CS方法得到的目标2维图像已经被虚假散射点淹没，算法失效。本文方法依然能够得到清晰的重构结果。图7为不同采样率条件下，本文方法与传统CS方法重构的图像熵以及目标背景比曲线。

图7中，本文方法重构得到的熵值明显小于传统方法，TBR值大于传统方法得到的结果，说明本文方法得到的图像凝聚性较好。因此说明本文方法成像性能优于传统方法，可以在较低的距离向采样率条件下实现目标的高精度重构。

仿真4 不同信噪比条件下成像性能仿真 假设其他条件不变，距离向采样率设置为0.8，图8分别为在不同信噪比条件下，本文方法与传统CS方法对目标进行成像的结果。

图8(a)中，随着信噪比的降低，传统CS方法得到的2维图像虚假散射点逐渐增多，在信噪比为5 dB时，成像结果已经存在大量虚假重构点，难以分辨目标的形状。而在图8(b)本文方法的仿真结果中，由于利用了回波信号的联合稀疏特性，当信噪比低至5 dB时，仍然能够较好的重构出目标图像。图9为不同信噪比条件下，本文方法与传统CS方法ISAR成像结果的熵值曲线以及TBR曲线。

图9中，本文方法得到的图像熵值始终小于传统CS方法，TBR值大于传统CS方法，说明本文方法成像效果好于传统方法成像效果。这与图8中的仿真结果一致，验证了本文方法具有较好的抗噪性能。

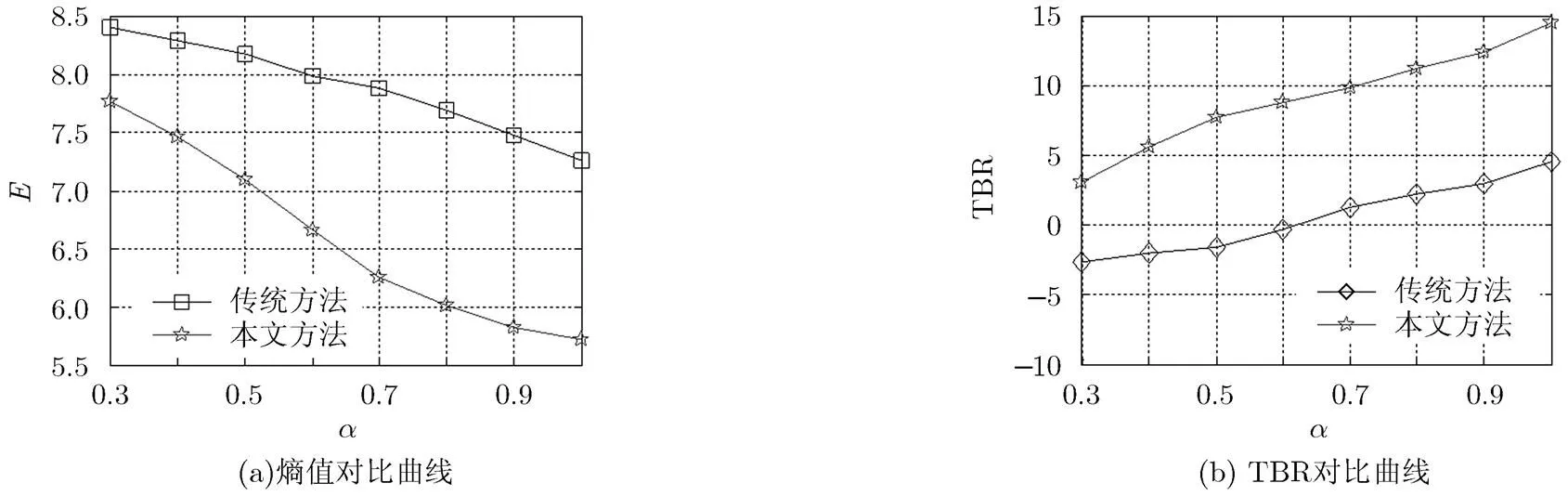
图7 不同采样率条件下重构的图像熵及目标背景曲线

图8 不同信噪比条件下成像性能

图9 不同信噪比条件下成像结果的熵值曲线和TBR曲线

6 结束语

本文在研究RCFS ISAR系统成像时，充分利用雷达电磁回波联合稀疏的特性，基于DCS理论实现了距离向的高精度重构，并得到最终的高分辨ISAR成像结果。通过理论分析与仿真实验证明该方法具有重构精度高、距离向采样率低和抗噪性能强等特点。在实际应用中，RCFS ISAR成像系统随机发射的子脉冲个数不可能随意减少，当子脉冲个数偏少时还会带来发射能量的降低等问题。另外，随着观测时间的增加，由目标转动引起的越距离单元走动影响将增大，这些问题将是下一步研究的重点。

参考文献

[1] DONOHO D L. Compressed sensing[J]., 2006, 52(4): 1289-1306.

[2] JIU Bo, LIU Hongchao, Liu Hongwei,. Joint ISAR imaging and cross-range scaling method based on compressive sensing with adaptive dictionary[J]., 2015, 63(5): 2112-2121.doi: 10.1109/TAP.2015.2409876.

[3] 田野, 张冰尘, 洪文. 基于分布式压缩感知的重轨干涉SAR形变检测方法与实验[J]. 中国科学院大学学报,2016, 33(1): 107-114. doi: 10.7523/j.issn.2095-6134.2016.01.016.

TIAN Ye, ZHANG Bingchen, and HONG Wen. Deformation detection approach for repeat-pass InSAR based on distributed compressed sensing[J]., 2016, 33(1): 107-114. doi: 10.7523/j.issn.2095-6134.2016.01.016.

[4] 李少东, 陈文峰, 杨军, 等. 任意稀疏结构的多量测向量快速稀疏重构算法研究[J]. 电子学报, 2015, 43(4): 708-715. doi: 10.396/j.issn.0372-2112.2015.04.012.

LI Shaodong, CHEN Wenfeng, YANG Jun,. Study on the fast sparse recovery algorithm via multiple measurement vectorsof arbitrary sparse structure[J]., 2015, 43(4): 708-715.doi:10.3969/j.issn.0372-2112.2015.04.012.

[5] ZHANG Shunsheng, ZHANG Wei, ZONG Zhulin,. High-resolution bistatic ISAR imaging based on two-dimensional compressed sensing[J].&, 2015, 63(5): 2098-2111. doi: 10.1109/TAP.2015.2408337.

[6] ERTIN E. Frequency diverse waveforms for compressive radar sensing[C]. Waveform Diversity & Design Conference, Niagara Falls, Ontario, Canada, 2010: 216-219.doi: 10.1109/WDD.2010.5592522.

[7] SUGAVANAM N and ERTIN E. Recovery guarantees for multifrequency chirp waveforms in compressed radar sensing[OL]. http://120.52.73.76/arxiv.org/pdf/1508.07969v1,2015.

[8] 孙延鹏, 王艺霖, 屈乐乐. 基于贝叶斯压缩感知的频率步进探地雷达成像算法[J]. 沈阳航空航天大学学报, 2015, 32(5): 68-73. doi: 10.3969/j.issn.2095-1248.2015.05.010.

SUN Yanpeng, WANG Yilin, and QU Lele. Stepped-frequency GPR imaging algorithm based on Bayesian compressive sensing[J]., 2015, 32(5): 68-73. doi: 10.3969/j.issn.2095-1248. 2015.05.010.

[9] 邵鹏, 邢孟道, 李学仕, 等. 一种新的频域带宽合成的斜视高分辨SAR成像方法[J]. 西安电子科技大学学报, 2015, 42(2): 28-34. doi: 10.3969/j.issn.1001-2400.2015.02.005.

SHAO Peng, XING Mengdao, LI Xueshi,. Squinted high resolution SAR based on the frequency synthetic bandwidth[J]., 2015, 42(4): 28-34. doi: 10.3969/j.issn.1001-2400.2015.02.005.

[10] SEYFRIED D and SCHOEBEL J. Stepped-frequency radar signal processing[J]., 2015, 112: 42-51.

[11] 王虹现, 梁毅, 邢孟道, 等. 基于稀疏线性调频步进信号的ISAR成像[J]. 中国科学：信息科学, 2011, 41(12): 1529-1540. doi: 1007/s11432-011-4353-1.

WANG Hongxian, LIANG Yi, XING Mengdao,. ISAR imaging via sparse frequency-stepped chirp signal[J]., 2011, 41(12): 1529-1540. doi: 1007/s11432-011-4353-1.

[12] ZHU Feng, ZHANG Qun, LUO Ying,. A novel cognitive ISAR imaging method with random stepped frequency chirp signal[J]., 2012, 55(8): 1910–1924. doi: 10.1007/s11432-012-4629-0.

[13] ZHANG Lei, QIAO Zhijun, XING Mengdao,. High-resolution ISAR imaging with sparse stepped-frequency waveforms[J]., 2011, 49(11): 4630-4651. doi: 10.1109/TGRS.2011. 2151865.

[14] 张榆红, 邢孟道, 徐刚. 基于稀疏孔径的联合稀疏约束干涉ISAR机动目标三维成像[J]. 电子与信息学报, 2015, 37(9): 2151-2157. doi: 10.11999/JEIT150125.

ZHANG Yuhong, XING Mengdao, and XU Gang. Joint sparsity constraint interferometric ISAR Imaging for 3-D geometry ofmaneuvering targets with sparse apertures[J].&, 2015, 37(9): 2151-2157. doi: 10.11999/JEIT150125.

[15] 陈一畅, 张群姗, 陈校平, 等. 多重测量矢量模型下的稀疏步进频率SAR成像算法[J]. 电子与信息学报, 2014, 36(12): 2986-2993. doi: 10.3724/SP.J.1146.2013.01831.

CHEN Yichang, ZHANG Qunshan, CHEN Xiaoping,. An imaging algorithm of sparse stepped frequency SAR based on multiple measurement vectors model[J].&, 2014, 36(12): 2986-2993. doi: 10.3724/SP.J.1146.2013.01831.

[16] 吴敏, 张磊, 邢孟道, 等. 基于分布式压缩感知的全极化雷达超分辨成像[J]. 电波科学学报, 2015, 30(1): 29-36. doi: 10.13443/j.cjors.2014041101.

WU Min, ZHANG Lei, XING Mengdao,. Full polarization super-resolution radar imaging algorithm based on distributedcompressive sensing[J]., 2015, 30(1): 29-36. doi: 10.13443/j.cjors. 2014041101.

[17] DUARTE M F, SARVOTHAM S, BARON D,. Distributed compressed sensing of jointly sparse signals[C]. Signals, Systems & Computers, Asilomar, CA, USA, 2005: 1537-1541. doi: 10.1109/ACSSC.2005.1600024.

[18] BARON D, DUARTE M F, WAKIN M B,. Distributed compressive sensing[OL]. http://arxiv. orb/pdf/0901. 3403v1, 2014.

[19] 丁鹭飞, 耿富录, 陈建春. 雷达原理(第5版)[M]. 北京:电子工业出版社, 2014: 1-2.

DING Lufei, GENG Fulu, and CHEN Jianchun. Radar Principles(5th)[M]. Beijing: Publishing House of Electronics Industry,2014: 1-2.

[20] SUNDMAN D. Greedy algorithms for distributed compressed sensing[D]. [Ph.D. dissertation], KTH Royal Institute of Technology, 2014: 99-116.

[21] DUARTE M F and ELDAR Y C. Structured compressed sensing: from theory to applications[J]., 2011, 59(9): 4053-4083. doi: 10.1109/ TSP.2011.2161982.

[22] DAVIES M E and ELDAR Y C. Rank awareness in joint sparse recovery[J]., 2010, 58(2): 1135-1146. doi: 10.1109/TIT.2011.2173722.

[23] 张磊. 高分辨SAR/ISAR成像及误差补偿技术研究[D]. [博士论文],西安电子科技大学, 2012.

ZHANG Lei. Study on high resolution SAR/ISAR imaging and error correction[D]. [Ph.D. dissertation], Xidian University, 2012.

[24] HUANG Yajing, WANG Xuezhi, LI Xiangli,. Inverse synthetic aperture radar imaging using frame theory[J]., 2012, 60(10): 5191-5200. doi: 10.1109/TSP.2012.2208107.

吕明久： 男，1985年生，博士生，研究方向为目标检测与识别技术.

李少东： 男，1987年生，博士生，研究方向为压缩感知在雷达成像中的应用.

杨 军： 男，1973年生，副教授，主要研究方向为雷达系统、雷达信号处理与检测理论.

马晓岩： 男，1962年生，教授，主要研究方向为雷达系统、雷达信号处理与检测理论、现代信号处理及其应用.

High Resolution ISAR Imaging Method Based on Random Chirp Frequency-stepped Signal

LÜ Mingjiu LI Shaodong YANG Jun MA Xiaoyan

(,430019,)

In order to make full use of the joint sparse physical characteristics of the radar echo to improve imaging performance. A novel super resolution Inverse SAR (ISAR) imaging method based on distributed compressed sensing theory is proposed. Firstly, the joint sparse echo model of the random chirp frequency-stepped signal is built and the pulse compression processing of each sub-pulse is processed. Secondly, owing to different random patterns of each group, different measurement matrices are constructed in accordance with the random pattern of sub-pulse signal. Then the corresponding compressed sensing model of the echo is built and the supper resolution range profile is obtained via the distributed compressed sensing theory. Finally, the supper resolution inverse synthetic aperture radar image can be obtained by a fast compressed sensing reconstruction algorithm, which is used to achieve the high resolution reconstruction in azimuth direction based on the sparse features. Theoretical analysis and simulation results show that the proposed method has the characteristics of high reconstruction accuracy, low sampling rate and strong anti-noise performance.

Inverse SAR (ISAR) imaging; Joint sparsity model; Distributed compressed sensing; Random chirp frequency-stepped signal

TN957.52

A

1009-5896(2016)12-3129-08

10.11999/JEIT160177

2016-03-01；改回日期：2016-09-01；

2016-10-17

吕明久 lv-mingjiu@163.com

国家自然科学基金(61671469)

The National Natural Science Foundation of China (61671469)