一种基于空域滤波的空间临近相干源角度估计方法

郑轶松 陈伯孝 杨明磊



一种基于空域滤波的空间临近相干源角度估计方法

郑轶松*陈伯孝 杨明磊

(西安电子科技大学雷达信号处理国家重点实验室 西安 710071) (西安电子科技大学信息感知技术协同创新中心 西安 710071)

相干源常见于存在多径的场景，如何解相干历来是阵列信号处理领域亟待解决的难题之一，特别针对空间临近相干源，其角度估计精度尚有待提高。针对空间临近相干源该文提出一种基于空域滤波的角度估计方法。首先利用空域滤波技术将多个相干源分离，再对滤波分离后的各个信号分别进行角度估计，并通过对滤波器系数和相干源角度的迭代优化提高测角精度。针对非均匀线阵，该方法采用虚拟阵列技术扩展其适用范围。计算机仿真结果表明该方法的测角精度较现有方法更高，信噪比较高时其测角的均方根误差可达克拉美罗界，验证了该方法的有效性和在空间临近相干源场景的优越性。

雷达信号处理；来波方向估计；空间临近相干源；空域滤波；解相干

1 引言

空间临近相干源是指存在于一个波束宽度内的多个相干源目标，常见于存在多径干扰的关键场景，如雷达低仰角目标探测与跟踪[1,2]。针对空间临近相干源，一般的处理方法是先对信号源进行解相干处理，再利用经典超分辨算法对其进行测角。空间临近相干源角度估计的关键在于解相干和超分辨，其中对相干源的处理历来是阵列信号处理领域亟待解决的难题之一。由多径引起的相干源往往导致信号协方差矩阵欠秩，严重影响了众多经典超分辨算法(如MUSIC(MUltiple SIgnal Classification)[4], ESPRIT(Estimation of Signal Parameters via Rotational Invariance Technique)[5])，使其无法直接应用于相干源测向。传统的解相干算法可分为两类：一是以空间平滑为代表的降维处理方法[6]，该类方法以牺牲阵列的有效孔径为代价消除信号源之间的相干性；第2类方法是非降维方法，如Toeplitz预处理技术[7]。Toeplitz技术无需牺牲阵列有效孔径，但是其角度估计精度较差，是有偏估计，因此无法逼近克拉美罗界。

近年来稀疏恢复与压缩感知技术[8]被大量应用于角度(Direction Of Arrival, DOA)估计领域，取得了众多令人瞩目的成果。基于稀疏恢复和压缩感知的DOA估计方法相比于传统超分辨算法有更低的信噪比门限，无需信源数的先验信息，且可直接应用于相干信号DOA估计中，无需解相干处理。基于稀疏恢复的DOA估计算法主要可分为两类，一是基于惩罚项的DOA估计算法，二是基于稀疏贝叶斯学习(Sparse Bayesian Learning, SBL)的DOA估计算法。其中基于惩罚项的DOA估计算法具有一定的超分辨性能，但是对于空间临近的目标，不论是相干源还是非相干源，随着目标间间隔的变小，由于感知矩阵列与列之间相关性的增强，其测角误差逐渐变大，即使在高信噪比下也难以逼近克拉美罗界，因此不适用于空间临近相干源的角度估计。另一类基于稀疏贝叶斯学习的DOA估计算法的重构和收敛误差较基于惩罚项的DOA估计算法更小，更易获得最优稀疏解，对于空间临近的非相干目标具有良好的分辨和测角性能[15]。但是对于空间临近的相干目标，稀疏贝叶斯学习方法在建模时引入一组相互独立的高斯分布超参数对信号功率谱进行描述，该假设与相干信号模型不符，导致测角误差增大，因此基于稀疏贝叶斯学习的DOA估计方法也无法针对空间临近相干源获得令人满意的测角结果。

空间临近相干源高精度角度估计方法的研究具有重要的现实意义，但是专门研究空间临近相干源的角度估计方法尚不多见，现有方法难以逼近克拉美罗界。为了解决空间临近相干源的角度估计问题，本文首先利用空域滤波技术对相干源进行滤波操作，将多个相干源分离为各个单个信号，进而对空域滤波后引入的非高斯噪声进行白化操作，最后利用Root-MUSIC算法对各个目标进行测角。另外，由于Root-MUSIC算法对阵列流型有一定要求，只适用于均匀线阵，因此本文提出利用虚拟阵列的方法，将非均匀线阵虚拟为均匀线阵，并对虚拟阵列引入的非高斯白噪声进行白化，使所提方法适用于非均匀阵列，扩展了所提方法的应用范围。

2 空间临近相干源角度估计方法

2.1 信号模型

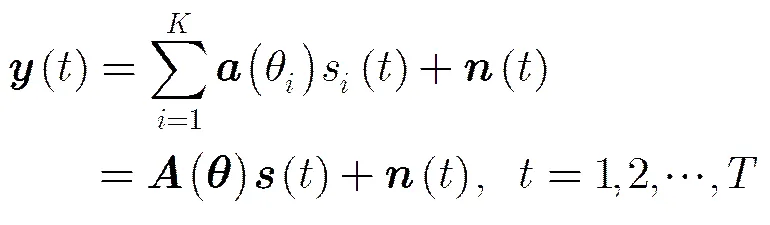
2.2 空域滤波器设计

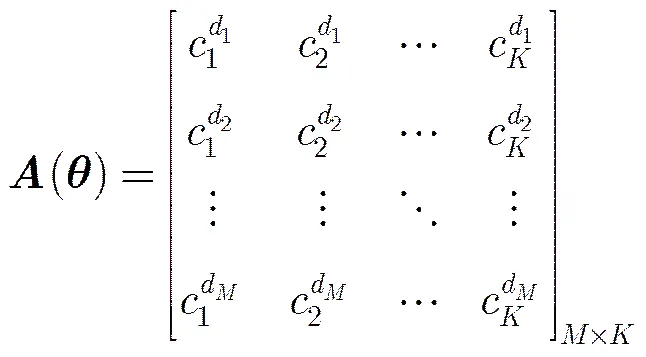
(3)

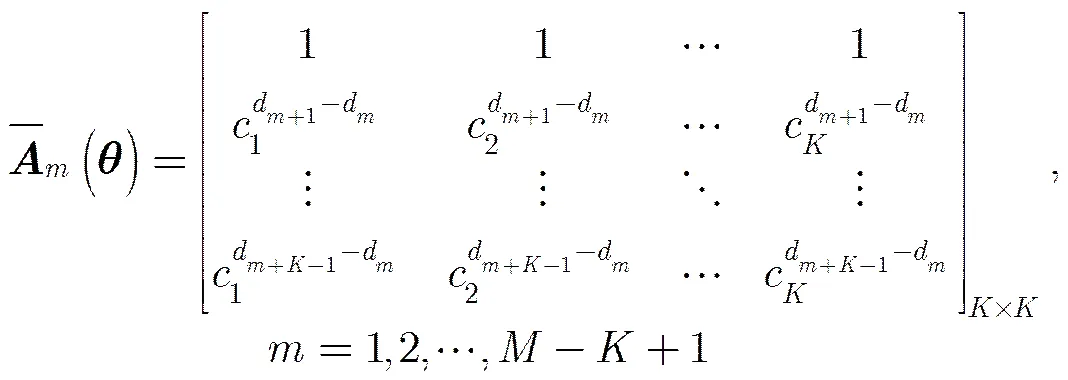
(5)

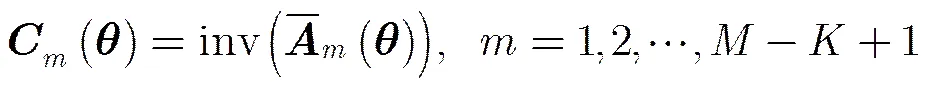
(7)

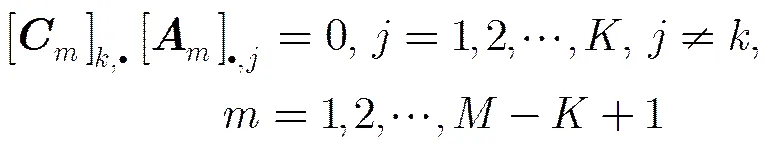
(9)

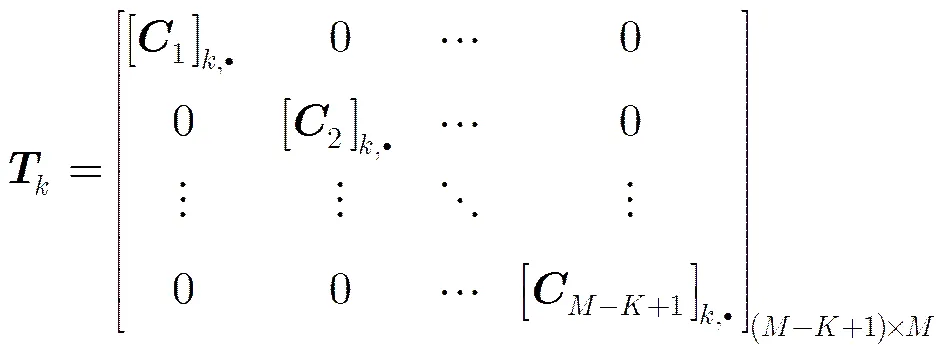
由式(8)和式(9)可得

(11)

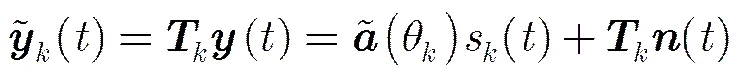
2.3 均匀线阵角度估计方法

由式(12)可知，空域滤波将各个相干源信号互相分离，无需解相干处理，但是也有其固有缺点，在此对其进行几点说明：一是空域滤波后带来阵列的孔径损失，由个自由度减为个自由度，这与空间平滑孔径损失类似。但是与空间平滑技术带来的孔径损失不同的是，空域滤波后的个输出中分别只包含一个信号，其余信号都被滤除，最大程度地消除了信号之间的干扰；而空间平滑技术只是恢复了信号协方差矩阵的秩，而没有将信号协方差矩阵变为对角阵，更无法消除各个信号之间的干扰，这也是空域滤波技术的角度估计精度比空间平滑技术高的根本原因。即使空域滤波带来了孔径损失，消除信号间的干扰带来的精度提升大大弥补了孔径损失带来的精度下降。因此针对空间临近相干源，大于信噪比门限时本文算法能逼近克拉美罗界，具体讨论见本文的计算机仿真部分。二是如式(12)所示，进行空域滤波后，噪声不再满足高斯白的条件，需要对其进行白化处理。三是空域滤波器的设计需要已知信号源的角度，为解决此问题，本文采用运算量较小的算法(如空间平滑预处理后的ESPRIT算法)进行角度初始估计，利用初始估计角度设计空域滤波器，得到新的角度估计后再设计新的空域滤波器参数，以此迭代求解，直至满足收敛条件。由于迭代求解的运算次数较多，本文采用无需空域搜索的Root-MUSIC算法进行DOA估计。综上所述，空域滤波的固有缺点都可通过技术手段克服，下面对后续处理进行介绍。

Root-MUSIC算法仅适用于均匀线阵，本节描述均匀线阵的DOA估计方法，非均匀线阵的DOA估计方法在2.4节进行讨论。如式(12)所示，空域滤波后噪声变为，由于空域滤波变换矩阵已知，因此可对滤波矩阵进行白化预处理，将噪声预白化为高斯白噪声，白化后的空域滤波矩阵如式(13)所示。

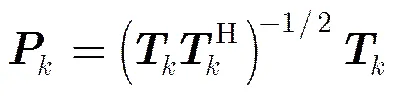
(14)

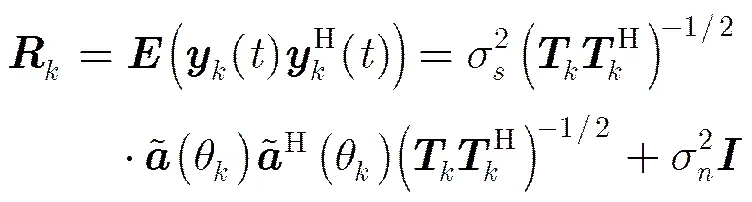
(16)

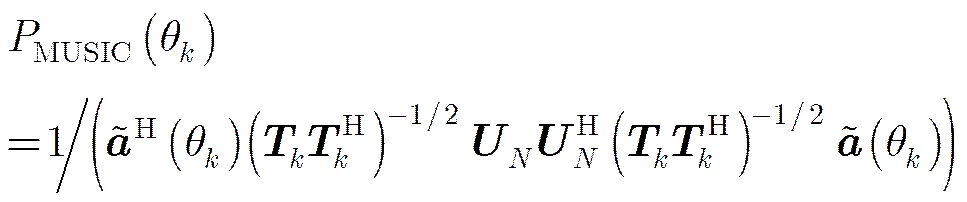
(18)

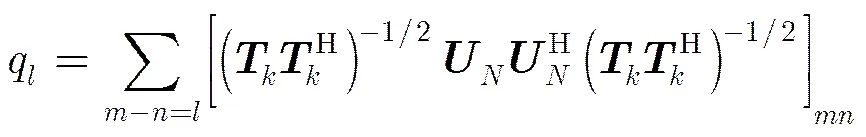
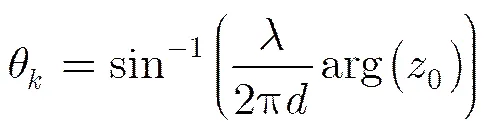
2.4 非均匀线阵角度估计方法

由2.2节可知，空域滤波器的设计对线阵是否均匀没有要求，因此需要设计适用于非均匀线阵的空间临近相干源测角方法。Root-MUSIC算法利用了均匀线阵导向矢量矩阵的Vandermonde性质，避免了空域搜索，但是对于非均匀线阵该方法不适用。针对非均匀线阵，最直观的解决方法是结合空域搜索的DOA估计方法(如MUSIC)实现空间临近相干源的角度估计。但是针对空域滤波后的空间临近相干源，空域搜索方法有其本质缺点：一是由于采用迭代优化的方法对空域滤波器系数和角度进行交替估计，随着迭代次数的增多，空域搜索方法计算量太大；二是当空域搜索角度间隔较大时，空域搜索方法对目标角度的估计易出现震荡的现象，导致算法无法收敛，而搜索角度间隔的减小又会导致运算量的急剧提升，这是空域搜索方法无法完全解决的一对矛盾。因此，为了使Root-MUSIC算法适用于非均匀阵列的空间临近相干源角度估计，本文采用虚拟阵列的方法，将非均匀线阵虚拟为均匀线阵，并通过白化预处理将虚拟阵列引入的噪声白化，使Root-MUSIC算法适用于非均匀阵列。

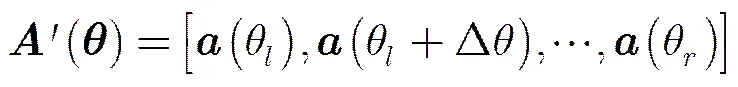
(22)

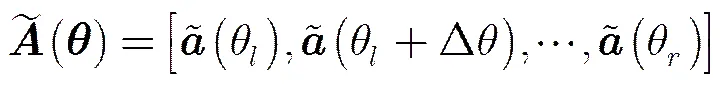
(24)

则虚拟阵列转换矩阵为[18]

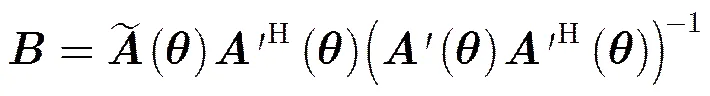
虚拟阵列预处理后的噪声不再是高斯白噪声，需要对噪声进行白化处理。白化后的虚拟阵列转换矩阵为。针对非均匀线阵的第个信号，需要先对接收信号进行虚拟阵列处理，再对其进行空域滤波，其白化后的虚拟阵列与空域滤波转换矩阵为

(26)

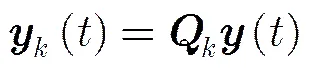
(28)

3 仿真实验与结果分析

3.1 SFRM与SFM算法收敛性能及运行时间比较

假设阵元数为10的均匀线阵，阵元间距半波长，半功率波束宽度为10.15，两相干目标入射角度分别为和，相干系数为1，信噪比为20 dB，快拍数为30。两相干目标角度间隔约为1/2半功率波束宽度，可认为是空间临近相干源。仿真比较各算法的收敛性能，图1中SFRM表示本文提出的空域滤波Root-MUSIC算法，SFM1和SFM2表示空域滤波MUSIC算法，其中SFM1算法空域搜索间隔为, SFM2算法空域搜索间隔为。由图1可以看出，初始角度偏离真实角度，分别为和。随着迭代次数的增加，SFRM算法和SFM1算法逐渐收敛接近真实值，而SFM2算法由于空域搜索间隔较大，对两相干目标的角度估计开始交替震荡，无法收敛至最优点。可见若将空域搜索间隔精细为0.01, SFM1算法相比于初始估计其精度有一定提升，但是搜索间隔越小，SFM算法的运算时间越长。因此对本仿真场景SFM和SFRM算法的平均运行时间进行统计，蒙特卡罗次数为100。设相干系数为相位随机，幅度为1的复数，其中SFM算法的角度搜索范围为至，角度搜索间隔分别取1.00, 0.50, 0.20, 0.10, 0.05, SFRM无需空域搜索，其余仿真参数不变，结果如表1所示。显然SFRM算法的平均运行时间大大小于SFM算法，而角度间隔0.05的SFM算法平均运行时间已经长达6.25 s，无法实际应用。因此综合考虑运行时间与精度，本文采用SFRM算法对空间临近相干源进行测角。

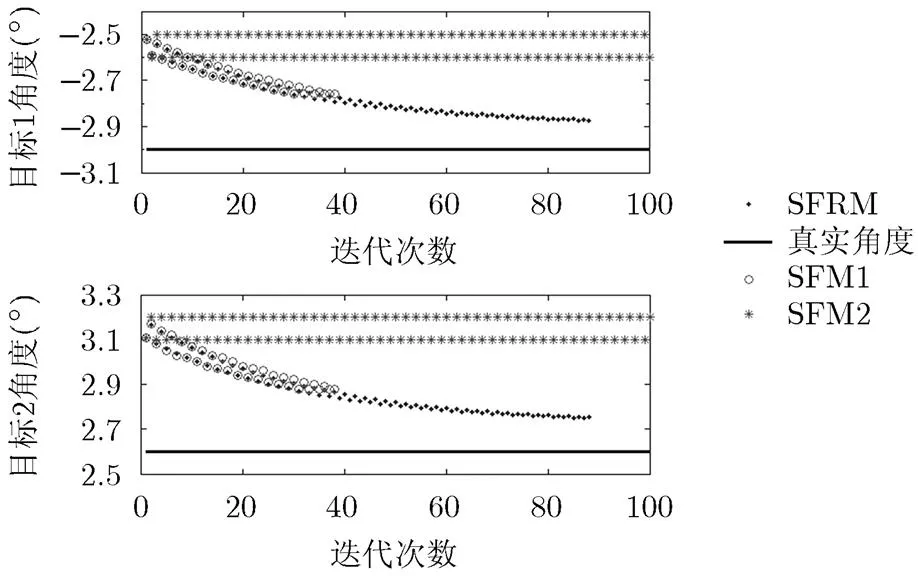
图1 SFRM和SFM算法收敛性能比较

3.2 均匀线阵角度估计性能随信噪比的变化

假设阵元间距半波长的均匀线阵，阵元数为10，两相干目标入射角度分别为和，相干系数为0.95+0.31j，快拍数为20，比较各算法性能与信噪比的关系，蒙特卡罗次数为100。图2中SFRM表示本文提出的空域滤波Root-MUSIC算法，SSMUSIC(Spatial Smoothing MUSIC)表示空间平滑MUSIC算法[6]，采用阶数为3的前后向空间平滑，SBL表示基于稀疏贝叶斯学习的DOA估计算法[14]，CRB(Cramer-Rao Bound)表示克拉美罗界。图中RMSE(Root Mean Square Error)为两目标RMSE的平均值。SBL由于算法模型与相干源的不匹配，无法得到高精度角度估计结果。SSMUSIC算法在高信噪比下测角效果较好，但是也不能逼近克拉美罗界，且信噪比门限比较高。SFRM算法在高信噪比下能逼近克拉美罗界，且其信噪比门限大大低于SSMUSIC算法，验证了其对空间临近相干源的优越性。

3.3 均匀线阵角度估计性能随相干系数相位的变化

相干源相干系数的相位对测角性能的影响很大，因此仿真考察相干系数相位对测角性能的影响。假设阵元间距半波长的均匀线阵，阵元数为10，两相干目标入射角度为，以第1个目标为参考信号，第2个信号的相干系数的相位为至，快拍数为30，信噪比为15 dB，蒙特卡罗次数为100。对于均匀线阵，若以阵列中心作为导向矢量参考点，算法测角性能及克拉美罗界与相干系数相位的关系如图3所示。测角性能与克拉美罗界关于相干系数相位对称。由于SSMUSIC算法的信噪比门限较高，在相干系数相位为,,附近SSMUSIC算法失效，即使在附近SSMUSIC算法也与克拉美罗界有一定距离，无法逼近克拉美罗界。SBL算法与SSMUSIC算法类似，且角度估计精度更差。本文所提的SFRM算法在所有不同相干系数的相位上都能逼近克拉美罗界，验证了本文所提算法的有效性。

表1 各算法平均运行时间

算法/角度搜索间隔SFM/1.00SFM/0.50SFM/0.20SFM/0.10SFM/0.05SFRM 平均运行时间(s)0.150.291.412.676.250.03

3.4 均匀线阵角度估计性能随目标间角度间隔的变化

一般来说，两相干目标角度间隔越小，测角精度越差，考察相干源间角度间隔对算法测角性能的影响。假设阵元间距半波长的均匀线阵，阵元数为10，以第1个目标为参考信号，第2个信号的相干系数为0.81+0.59j，快拍数为30，信噪比为15 dB，蒙特卡罗次数为100。阵列半功率波束宽度为，令两相干源目标间角度间隔为至，仿真结果如图4所示。SSMUSIC算法在角度间隔大于时有效，但无法完全达到克拉美罗界。SFRM算法在角度间隔大于时即可达到克拉美罗界。SBL算法的均方根误差则始终与克拉美罗界存在较大距离，即使在角度间隔为8°时测角精度也无法逼近克拉美罗界。因此SFRM算法较现有算法能处理角度间隔更小的相干源，精度更高，尤其适用于空间临近相干源场景。

3.5 非均匀线阵角度估计性能随信噪比的变化

考察所提VSFRM算法对非均匀阵列的有效性，设阵元数为10的非均匀线阵，波长为，以第1个阵元作为参考点，各阵元位置为，阵列孔径为。两相干目标入射角度为，以第1个目标为参考信号，相干系数为0.54+0.84j。由于整个阵列孔径为4.50倍波长，可将原阵列虚拟为阵元间隔半波长的均匀阵列。图5中VSFRM表示针对非均匀阵列的虚拟阵列空域滤波Root-MUSIC算法，SSMUSIC算法不能直接适用于非均匀线阵，因此省去对SSMUSIC的性能仿真，SBL表示稀疏贝叶斯学习DOA估计算法，其超完备基根据阵元实际位置设计，可直接适用于非均匀阵列。结果如图5所示，可见SBL算法即使在高信噪比下也无法逼近克拉美罗界，而VSFRM算法在大于8 dB时即达到克拉美罗界，验证了虚拟阵列、空域滤波和白化预处理等方法在非均匀线阵下的有效性，扩展了所提方法的应用范围。

3.6 角度估计性能随预估值偏差的变化

由于本文算法性能与预估值的准确程度相关，因此考察角度估计性能与初始预估计值的关系。假设阵元间距半波长的均匀线阵，阵元数为10，以第1个目标为参考信号，第2个信号的相干系数为0.88 +0.48j，快拍数为20，信噪比为15 dB，蒙特卡罗次数为200。阵列半功率波束宽度为，令两相干源入射角度分别为和。设预估值与真实值的最大偏差为，预估值与真实值的偏差满足的均匀分布，仿真中预估值最大偏差的变化范围为至，仿真预估值偏差对SFRM算法的测角性能的影响。结果如图6所示，此情形下CRB为，而当预估值的最大偏差小于时，SFRM算法都可通过空域滤波和迭代求解，使最终结果达到CRB，说明所提SFRM算法对预估值具有很好的性能提升效果。

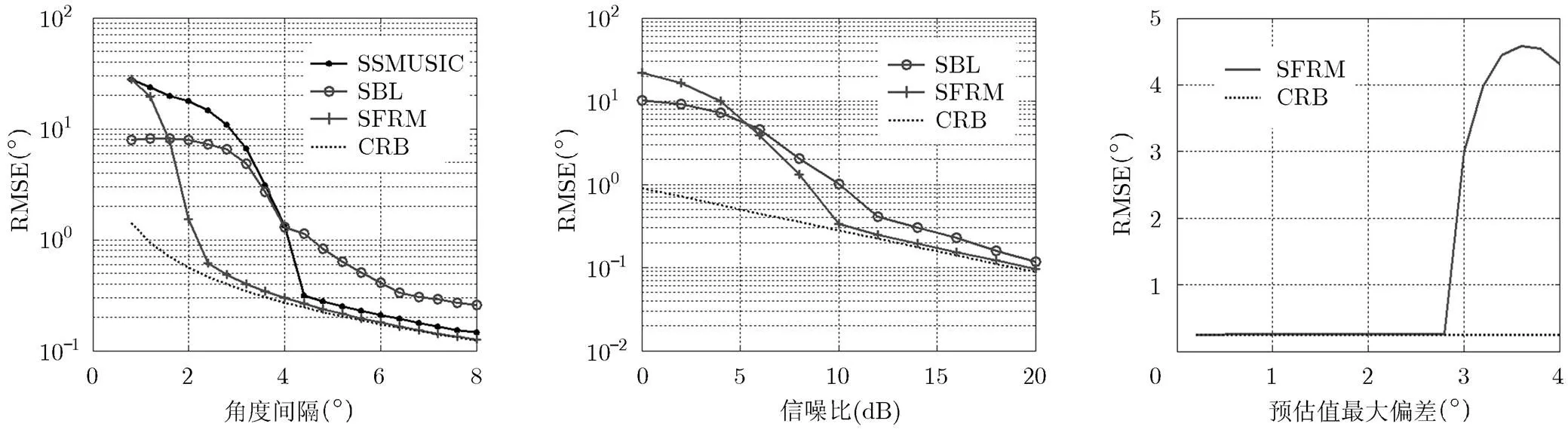
图4 均匀线阵角度估计性能      图5 非均匀线阵角度估计      图6 双目标角度估计性能

随目标间角度间隔变化图       性能随信噪比变化图       随预估值偏差变化图

4 结束语

本文针对空间临近相干源场景提出一种基于空域滤波和Root-MUSIC的高精度角度估计方法，通过空域滤波将相干源彼此分离以减轻相互间的干扰，对滤波器系数和相干源角度迭代优化以提高角度估计精度，并利用虚拟阵列技术使本文方法适用于非均匀阵列。Root-MUSIC方法无需空域搜索的优点一方面大大减少了本文方法的运算量，另一方面避免了空域搜索类算法角度搜索间隔较大时无法收敛陷入震荡的缺点，保证了本文方法的收敛性能。计算机仿真分析了信噪比、相干系数相位和目标间角度间隔对算法性能的影响，结果表明本文方法相比现有算法具有信噪比门限低，性能逼近克拉美罗界等优点。与空间平滑类似，空域滤波技术也是通过阵列孔径损失换取相干源的分离，但是二者不同的是，空间平滑技术只能恢复协方差矩阵的秩，而空域滤波理论上能消除信号间的干扰，因此能得到更好的角度估计性能，为空间临近相干源的处理提供了一种新思路。

参考文献

[1] 刘源, 王洪先, 纠博, 等. 米波MIMO雷达低空目标波达方向估计新方法[J]. 电子与信息学报, 2016, 38(3): 622-628. doi: 10.11999/JEIT150555.

LIU Yuan, WANG Hongxian, JIU Bo,. A new method for DOA estimation for VHF MIMO radar in low-angle tracking environment[J].&, 2016, 38(3): 622-628. doi: 10.11999/ JEIT150555.

[2] 郑轶松, 陈伯孝. 米波雷达低仰角目标多径模型及其反演方法研究[J]. 电子与信息学报, 2016, 38(6): 1468-1474. doi: 10.11999/JEIT151013.

ZHENG Yisong and CHEN Baixiao. Multipath model and inversion method for low-angle target in very high frequency radar[J].&, 2016, 38(6): 1468-1474. doi: 10.11999/JEIT151013.

[3] KRIM H and VIBERG M. Two decades of array signal processing research: the parametric approach[J]., 1996, 13(4): 67-94. doi: 10.1109/79. 526899.

[4] SCHMIDT R. Multiple emitter location and signal parameter estimation[J]., 1986, 34(3): 276-280. doi: 10.1109/TAP.1986. 1143830.

[5] ROY R and KAILATH T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]., 1989, 37(7): 984-995. doi: 10.1109/29.32276.

[6] SHAN Tiejun, WAX M, and KAILATH T. On spatial smoothing for direction-of-arrival estimation of coherent signals[J].,,, 1985, 33(4): 806-811. doi: 10.1109/TASSP. 1985.1164649.

[7] KUNG S, LO C, and FOKA R. A Toeplitz approximation approach to coherent source direction finding[C], Japan, 1986: 193-196.

[8] DONOHO D L. Compressed sensing[J]., 2006, 52(4): 1289-1306. doi: 10.1109/ TIT.2006.871582.

[9] HE Z Q, LIU Q H, JIN L N,. Low complexity method for DOA estimation using array covariance matrix sparse representation[J]., 49(3): 228-230. doi: 10.1049/el.2012.4032.

[10] WEI Cui, TONG Qian, and JING Tian. Enhanced covariances matrix sparse representation method for DOA estimation[J]., 2015, 51(16): 1288-1290. doi: 10.1049/el.2014.4519.

[11] LIU Hongqing, ZHAO Liuming, LI Yong,. A sparse- based approach for DOA estimation and array calibration in uniform linear array[J]., 2016, 16(15): 6018-6027. doi: 10.1109/JSEN. 2016.2577712.

[12] WANG Yi, YANG Minglei, CHEN Baixiao,. Improved DOA estimation based on real-valued array covariance using sparse Bayesian learning[J].2016, 129: 183-189. doi: 10.1016/j.sigpro.2016.06.002.

[13] WANG Lu, ZHAO Lifan, BI Guoan,. Novel wideband DOA estimation based on sparse Bayesian learning with dirichlet process priors[J]., 2016, 64(2): 275-289. doi: 10.1109/TSP.2015. 2481790.

[14] YANG Zai, XIE Lihua, and ZHANG Cishen. Off-grid direction of arrival estimation using sparse Bayesian inference[J]., 2013, 61(1): 38-43. doi: 10.1109/TSP.2012.2222378.

[15] ZHANG Zhilin and RAO B D. Sparse signal recovery with temporally correlated source vectors using sparse Bayesian learning[J]., 2011, 5(5): 912-926. doi: 10.1109/JSTSP.2011. 2159773.

[16] LIU Zhangmeng, LIU Zheng, FENG Daowang,. Direction-of-arrival estimation for coherent sources via sparse Bayesian learning[J]., 2014, (2014): 1-8. doi: 10.1155/2014/959386.

[17] TEAGUE C C. Root-MUSIC direction finding applied to multifrequency coastal radar[C].Toronto, Canada, 2002: 1896-1898.

[18] FRIEDLANDER B and WEISS A J. Direction finding using spatial smoothing with interpolated arrays[J], 1992, 28(2): 574-587. doi: 10.1109/7.144583.

郑轶松： 男，1990年生，博士生，研究方向为阵列信号处理、米波雷达低仰角测高方法.

陈伯孝： 男，1966年生，教授，博士生导师，研究方向包括新体制雷达系统设计及其实现、雷达信号处理、目标精确制导与跟踪等.

杨明磊： 男，1981年生，副教授，硕士生导师，研究方向为新体制雷达系统设计、阵列信号处理等.

Direction of Arrival Estimation Method for Spatially Adjacent Coherent Sources Based on Spatial Filtering

ZHENG Yisong CHEN Baixiao YANG Minglei

(,,710071,) (,710071,)

Coherent sources commonly exist in scenarios with multipath effect. How to decorrelate coherent sources is traditionally a problem urgently to be solved in the array signal processing domain. Especially for spatially adjacent coherent sources, the performance of the estimation of Direction Of Arrival (DOA) remains to be improved. A DOA estimation method based on spatial filtering is proposed for spatially adjacent coherent sources. Multiple coherent sources are separated by spatial filtering and the DOAs are estimated respectively afterwards. The performance of the DOA estimation is enhanced by refining the filter parameters and the DOAs of the coherent sources iteratively. To extend its application to non-uniform linear array, the virtual array technique is adopted. The computer simulation results indicate that the proposed algorithm has better DOA estimation performance than the existing methods. In the scenario of sufficiently high Signal to Noise Ratio (SNR), the Root Mean Square Error (RMSE) could achieve Cramer-Rao Bound (CRB). The effectiveness and the superiority of the proposed method for spatially adjacent coherent sources are validated by the simulation results.

Radar signal processing; DOA estimation; Spatially adjacent coherent sources; Spatial filtering; Decorrelation

TN957.51

A

1009-5896(2016)12-3100-07

10.11999/JEIT160882

2016-08-26；改回日期：2016-11-04；

2016-12-02

郑轶松 zhengys90@163.com

国家自然科学基金(61571344)，上海航天科技创新基金(SAST2015071, SAST2015064)

The National Natural Science Foundation of China (61571344), The Funds of SAST (SAST2015071, SAST 2015064)