一种基于SAR稀疏采样数据的动目标运动参数估计方法

陈一畅 张 群



一种基于SAR稀疏采样数据的动目标运动参数估计方法

陈一畅*①②张 群①③

①(空军工程大学信息与导航学院 西安 710077)②(清华大学电子工程系 北京 100084)③(复旦大学电磁波信息科学教育部重点实验室 上海 200433)

该文针对地面动目标运动参数估计问题进行研究，提出一种利用单天线合成孔径雷达(SAR)稀疏采样数据的动目标2维速度估计方法。首先以目标2维速度为参数构建一个等效参数化模型将动目标回波数据转化为小斜视回波数据，然后利用改进的迭代阈值算法实现不同参数条件下的动目标2维成像，最后以成像结果的图像熵值为优化准则对初始模型参数进行搜索，从而获得准确的动目标运动参数。该方法以稀疏采样数据为输入，可以减少所需数据量，并且能够有效避免多普勒模糊问题，在较低信杂比条件下仍然能够准确估计出目标运动参数。仿真实验结果验证了所提动目标参数估计方法的有效性。

合成孔径雷达；参数化模型；运动目标；参数估计

1 引言

合成孔径雷达(SAR)是一种装载在航空航天平台，具备对地全天候、全天时成像能力的微波遥感设备[1]。其中对地面动目标运动参数估计是SAR的一项重要应用，准确的运动参数估计对于动目标检测、成像、识别都有着重要作用。传统的动目标运动参数估计方法大多是基于Doppler相位分析，通过估计出回波信号的Doppler频偏和Doppler调频率，从而计算出动目标在距离向和方位向的2维速度参数[2,3]。但是这一类方法存在固有缺陷，当SAR以一定的脉冲重复频率(PRF)在方位向采样时，只可对区间内的Doppler频谱进行分析，而当目标运动速度较快时，可能使得Doppler频偏超出此区间，即Doppler模糊，最终使得目标速度估计存在较大误差。解决Doppler模糊问题最简单直接的办法是增大PRF，但是同时又会引入缩短模糊距离、增加数据量等新问题。许多文献基于多通道SAR系统提出了有效的动目标速度估计方法，以及动目标成像算法[4,5]，然而，需要指出的是多通道解决Doppler模糊问题的同时也增加了硬件复杂度。也有文献针对单天线SAR数据，提出了动目标参数估计方法，如文献[6]，将动目标信号做距离徙动矫正(Range Cell Migration Correction, RCMC)和距离压缩操作，然后以距离多普勒域的图像对比度最大化为准则，对目标的2维速度进行搜索。因为RCMC和距离压缩操作与目标速度密切相关，所以只有根据准确的目标运动参数对信号进行RCMC和距离压缩才能使距离多普勒图像的对比度最大化。文献[6]的方法可以有效克服Doppler模糊，但对信杂比有较高的要求。文献[7]利用Radon变换估计目标径向速度，避免了Doppler模糊问题，然后采用一种“双向分段成像”方法估计目标方位向速度。所谓的“双向分段成像”方法是利用前后两段部分孔径数据分别对动目标进行粗成像，然后根据两幅粗像的位置差异计算方位向速度，获得的估计精度有限。

需要指出的是上述动目标运动参数估计方法大都是基于SAR全采样数据的估计方法。近年来，压缩感知理论被广泛地引入到SAR应用中，一系列基于稀疏降采样数据的方法被提出，主要用于SAR数据压缩[8]，提高SAR图像分辨率[9,10]，SAR平台运动补偿[11]等方面。稀疏采样方式是未来SAR实际应用中一个重要发展方向，因此有必要研究基于稀疏采样数据的动目标运动参数估计方法。

参数化稀疏表征是字典学习的一个特殊分支，能够实现雷达探测过程中未知参数的动态学习和雷达信号的最优稀疏表征[12]，其概念最早在文献[13]中提到，被用于逆合成孔径雷达(Inverse Synthetic Aperture Radar, ISAR)成像。文献[12]综述了参数化稀疏表征在雷达探测中的应用，重点介绍了参数化稀疏表征在ISAR成像、SAR自聚焦和目标识别中的应用。本文结合压缩感知理论，将目标运动参数作为影响观测模型的唯一变量，通过优化动目标成像结果的稀疏性来估计目标的运动参数。文章首先分析了动目标回波信号稀疏采样数据的特点，然后构建一个转换模型，将动目标回波信号转换为等效的斜视SAR回波信号。可以证明，等效后的平台速度、斜视角与原动目标模型中目标2维速度成一一对应关系。利用作者前期提出的斜视SAR压缩感知成像算法[14]，实现动目标的粗成像。在目标2维速度速度域进行搜索，所选取的2维速度越接近真值，所获得的成像结果聚焦性能将越好。最终本文以图像熵最小化为准则，在2维速度域估计出动目标径向和方位向2维速度。本文方法可以克服Doppler模糊问题，相比于传统方法，可以采用稀疏采样数据完成对动目标的运动参数精确估计，减少了所需数据量的同时获得较高的估计精度。文章采用仿真数据进行了实验，说明了本文算法的有效性，并且讨论了信杂比对本文估计方法的影响，分析了本文估计方法对目标径向速度和方位向速度的估计精度。

2 信号模型

本文考虑传统单天线SAR系统，工作模式为正侧视条带式，SAR平台与观测场景2维示意图如图1(a)所示。假定SAR装载在飞机平台上，并沿着轴以速度做匀速直线飞行。假设观测场景中有一动目标P，径向速度分量记为(以靠近SAR平台飞行轨迹方向为正方向)，方位向速度分量记为(以SAR平台速度方向为正方向)，即我们需要估计的参数。为了便于说明方法推导，我们首先采用全采样数据进行模型分析。SAR平台以“走停”模式发射并接受信号，脉冲重复频率记为PRF。图1中标出了各虚拟合成孔径阵元位置。不失一般性，我们假设目标处于SAR平台正侧方时坐标为，其中0表示方位向坐标，表示距离向坐标，并以当前时刻为慢时间零点。则动目标与SAR瞬时距离为

本文采用线性调频(Linear Frequency Modulation, LFM)信号作为SAR发射信号，运动参数为的运动目标回波可以表示为

(2)

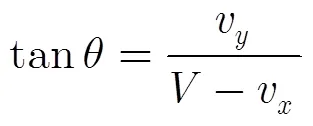
(4)

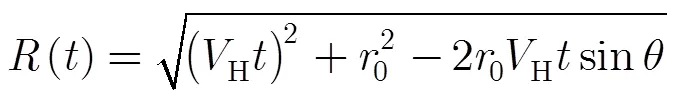
(6)

在全采样数据条件下，可以采用多种经典算法对斜视模型信号进行成像处理，如非线性频调变标算法(Non-linear Chirp Scaling, NCS)，距离徙动算法(Range Migration Algorithm, RMA)等。本文所建立的模型在距离向上对回波信号采用随机稀疏采样方式，其采样结果可以看作是全采样数据在距离向上的随机降维观测。对于稀疏采样数据，传统算法将不再适用，因此本文利用前期工作中提出的基于NCS算子的斜视SAR压缩感知成像方法对动目标回波稀疏采样数据进行成像[14]，然后根据成像结果估计动目标参数，具体操作步骤在第3节论述。

3 基于稀疏采样数据的动目标运动参数估计

(8)

(10)

上述方法是在合速度和斜视角确定情况下的稀疏采样数据目标成像方法，针对运动参数未知的运动目标，其等效得出的合速度和斜视角也是未知的。采用不同的运动参数进行上述过程求解，可以获得不同的成像结果，因此目标像可以看作是目标速度参数的隐函数。当与实际参数匹配时，才能得到清晰的目标2维像。图像熵是常用的衡量复图像清晰度的指标[19]，因此本文采用熵值最小化为优化目标，在2维速度空间内估计目标运动参数。复图像的计算公式为

(12)

步骤1 在整幅SAR图像中提取感兴趣的动目标区域，并将其转换到原始数据域；

步骤2 对2维速度空间离散化，并根据式(3)将离散点从2维速度空间映射到合速度-斜视角空间，利用ITA算法求解式(10)所述稀疏重构问题；

步骤3 根据式(11)计算重构结果的图像熵；

关于上述速度估计方法，需要说明两点：第一，动目标在整个SAR观测场景中往往是稀疏分布的，具有空间稀疏性，且步骤1可以去除部分背景杂波，提高动目标局部信杂比；第二，在搜索图像最小熵时，可以采取变步长搜索方式，首先采用大步长搜索减少运算时间，然后在极值附近采用小步长搜索提高估计精度。

4 实验结果与性能分析

本节采用仿真数据验证本文方法的有效性，并根据实验结果分析本文方法性能。实验中用到的SAR主要参数如下：SAR平台速度，载波波长，发射信号带宽，脉宽，天线实际孔径长度，脉冲重复频率，场景中心与SAR平台飞行轨迹之间的距离为，距离向全采样点数为。观测场景如图2所示，尺寸为，其中包含若干静止散射点，A为匀速运动目标，其方位向速度分量为，距离向速度分量为。根据动目标Doppler中心计算公式，可以得到，已经超出，因此会出现Doppler模糊。

首先，我们通过实验验证本文所构建的转换模型的正确性。对距离向数据进行随机稀疏采样，仅录取个采样点，定义降采样率为。图3(a)是采用模型参数获得的成像结果，其中静止目标可以获得准确聚焦结果，但是运动目标无法正常聚焦，并且其散焦效应使得静止散射点成像受到干扰。图3(b)采用本文模型对动目标进行成像，最终获得整个场景的准确重构结果，实验结果说明了采用本文所提出的等效斜视模型，在运动参数确定的情况下可以实现对运动目标的准确成像。

在运动目标运动参数未知情况下，利用本文方法对运动参数进行估计，仿真实验中设定信杂比为。以SAR平台速度的20%为运动参数估计区间，即在仿真实验中，与搜索范围均为。计算各搜索点的图像熵值，结果如图4。因为图中纵轴采用负熵值坐标，因此峰值位置对应了最小熵位置，从图4中可以看出峰值位置对应的运动参数估计结果为，这与目标运动参数真值完全一致。本文方法提供了目标在方位向和距离向2个维度上的速度分量，图5给出了熵值图在两个维度上剖面图，通过对比方位向和距离向速度-熵值剖面图，可以看出图5(a)中方位向熵值图的峰值宽度明显小于图5(b)中距离向熵值图的峰值宽度。这与实际情况相符，方位向的速度误差对图像散焦影响更大。为了进一步分析本文所提估计方法的性能，在不同信杂比条件下，分别考察方位向和距离向速度参数的估计精度，同时分析降采样率对估计精度的影响。图6给出了不同条件下，估计结果的相对误差结果，其中最小搜索步长为。从图中可以看出随着信杂比的提高，相对误差逐渐减小。降采样率为条件下，当信杂比达到6 dB以上时，方位向速度分量和距离向速度分量估计结果的相对误差均可控制在2.5%以内。此外，本文算法处理过程中用到了稀疏重构理论，降采样率队估计精度有一定影响，随着估计降采样率增大，相对误差也有所增大。

图2 观测场景           图3 稀疏采样回波重构结果

图4 2维速度空间动目标粗像熵值分布图

图5 目标粗像熵值1维剖面图

图6 动目标速度参数相对误差与信杂比(SCR)关系曲线

当场景中有多个不用运动参数的运动目标时，可以通过图像分割的方法分别估计不同目标的运动参数。若不同目标散焦图像之间有重叠，无法分离，也可采用本文方法同时估计2个目标的运动参数。以前一节仿真实验为例，将图2中B目标更改为运动目标，其2维运动参数为。图7给出了包含估计结果信息的熵值图，图中出现两个峰值，分别对应两个运动目标的运动参数。

图7 双目标2维速度空间动目标粗像熵值分布图

5 结束语

本文根据速度合成原理将SAR动目标观测模型转换为斜视SAR观测模型，然后利用改进的ITA算法对动目标回波稀疏采用数据进行处理，以动目标粗像熵值最小化为准则，在2维速度空间估计动目标的运动参数。利用本文提出的动目标运动参数估计方法，可以准确估计出稀疏采样数据条件下的动目标运动参数，在降采样率条件下，当信杂比达到6 dB时，估计值的相对误差可以控制在2.5%以内。此外，本文估计方法还可以克服Doppler模糊，并且能够同时实现多个目标运动参数的估计，本文采用仿真数据对模型正确性和算法性能进行了验证分析。下一步工作重点是设计相应的迭代算法，实现熵值最小化。

参考文献

[1] SAEEDI J and FAEZ K. Synthetic aperture radar imaging using nonlinear frequency modulation signal[J]., 2016, 52(1): 99-110. doi: 10.1109/TAES.2015.140310.

[2] WERNESS S A S, CARRARA W G, JOYCE L S,. Moving target imaging algorithm for SAR data[J]., 1990, 26(1): 57-67. doi: 10.1109/7.53413.

[3] PERRY R P, DIPIETRO R C, and FANTE R L. SAR imaging of moving targets[J]., 1999, 35(1): 188-200. doi: 10.1109/7.745691.

[4] ZHANG Shuangxi, XING Mengdao, XIA Xianggen,. Robust clutter suppression and moving target imaging approach for multichannel in azimuth high-resolution and wide-swath synthetic aperture radar[J]., 2015, 53(2): 687-709. doi: 10.1109/TGRS.2014.2327031.

[5] GUO Bin, VU Duc, XU Luzhou,. Ground moving target indication via multichannel airborne SAR[J]., 2011, 49(10): 3753-3764. doi: 10.1109/TGRS.2011.2143420.

[6] LI Gang, XIA Xianggen, XU Jia,. A velocity estimation algorithm of moving targets using single antenna SAR[J]., 2009, 45(3): 1052-1062. doi: 10.1109/TAES.2009.5259182.

[7] HOU Lili, SONG Hongjun, ZHENG Mingjie,. Fast moving target imaging and motion parameters estimation based on Radon transform and bi-directional approach[J].,&, 2016, 10(6): 1013-1023. doi: 10.1049/iet-rsn.2014.0567.

[8] 陈一畅, 张群, 朱丽莉, 等. 基于压缩感知和矢量量化的 SAR 数据级联压缩方法[J]. 现代雷达, 2013, 35(10): 36-40. doi: 10.16592/J.CNKI.1004-7859.2013.10.013.

CHEN Yichang, ZHANG Qun, ZHU Lili,. A cascade compress method of SAR data based on compressed sensing and vector quantization[J]., 2013, 35(10): 36-40. doi: 10.16592/J.CNKI.1004-7859.2013.10.013.

[9] BU Hongxia, TAO Ran, BAI Xia,. A novel SAR imaging algorithm based on compressed sensing[J]., 2015, 12(5): 1003-1007. doi: 10.1109/LGRS.2014.2372319.

[10] 陈一畅, 张群, 陈校平, 等. 多重测量矢量模型下的稀疏步进频率SAR成像算法[J]. 电子与信息学报, 2014, 36(12): 2986-2993. doi: 10.3724/SP.J.1146.2013.01831.

CHEN Yichang, ZHANG Qun, CHEN Xiaoping,. An imaging algorithm of sparse stepped frequency SAR based on multiple measurement vectors model[J].&, 2014, 36(12): 2986-2993. doi: 10.3724/SP.J.1146.2013.01831.

[11] GU Fufei, ZHANG Qun, CHI Long,. A novel motion compensating method for MIMO-SAR imaging based on compressed sensing[J]., 2015, 15(4): 2157-2165. doi: 10.1109/JSEN.2014.2371451.

[12] 李刚, 夏香根. 参数化稀疏表征在雷达探测中的应用[J]. 雷达学报, 2016, 5(1): 1-7. doi: 10.12000/JR15126.

LIGang and XIA Xianggen. Parametric sparse representation and its applications in radar sensing[J]., 2016, 5(1): 1-7. doi: 10.12000/JR15126.

[13] RAO W, LI G, Wang X,. Parametric sparse representation method for ISAR imaging of rotating targets[J]., 2014, 50(2): 910-919. doi: 10.1109/TAES.2014. 120535.

[14] 顾福飞, 张群, 杨秋, 等. 基于NCS算子的大斜视SAR压缩感知成像方法[J]. 雷达学报, 2016, 5(1): 16-24. doi: 10.12000 /JR15035.

GU Fufei, ZHANG Qun, YANG Qiu,. Compressed sensing imaging algorithm of high-squint SAR based on NCS operator[J]., 2016, 5(1): 16-24. doi: 10. 12000/JR15035.

[15] 李震宇, 梁毅, 邢孟道, 等. 弹载合成孔径雷达大斜视子孔径频率相位滤波成像算法[J]. 电子与信息学报, 2015, 37(4): 954-959. doi: 10.11999/JEIT140618.

LI Zhenyu, LIANG Yi, XING Mengdao,. A frequency phase filtering imaging algorithm for highly squint missile-borne synthetic aperture radar with subaperture[J].&, 2015, 37(4): 954-959. doi: 10.11999/JEIT140618.

[16] 江淮, 赵惠昌, 汉敏, 等. 基于DFT滤波器组的大斜视SAR成像算法[J]. 电子与信息学报, 2016, 38(1): 104-110. doi: 10.11999/JEIT150381.

JIANG Huai, ZHAO Huichang, HAN Min,. Highly squint SAR imaging algorithm based on DFT filter banks[J].&, 2016,38(1): 104-110. doi: 10.11999/JEIT150381.

[17] 杨军, 李震宇, 孙光才, 等. 一种新的大斜视TOPS SAR全孔径成像方法[J]. 西安电子科技大学学报(自然科学版), 2015, 42(1): 42-48. doi: 10.3969/j.issn.1001-2400.2015.01.08.

YANG Jun, LI Zhenyu, SUN Guangcai,. Novel full aperture imaging algorithm for highly squinted TOPS SAR[J].(), 2015, 42(1): 42-48. doi: 10.3969 /j.issn.1001-2400.2015.01.08.

[18] FANG Jian, XU Zongben, ZHANG Bingchen,. Fast compressed sensing SAR imaging based on approximated observation[J]., 2014, 7(1): 352-363. doi: 10.1109/JSTARS.2013.2263309.

[19] KRAGH T J and KHARBOUCH A A. Monotonic iterative algorithm for minimum-entropy autofocus[C]. IEEE International Conference on Image Processing, Atlanta, 2006: 645-648.

陈一畅： 男，1988年生，博士生，研究方向为稀疏微波成像.

张 群： 男，1964年生，教授，博士生导师，主要研究方向包括雷达信号处理、电子对抗.

Parameter Estimation Method of Moving Targets with SAR Sparse Sampling Data

CHEN Yichang①②ZHANG Qun①③

①(,,710077,)②(,,100084,)③(,,200433,)

To solve the problem of motion parameter estimation of ground moving target, a parameter estimation method of moving targets with sparse sampling data of single SAR sensor is proposed. First, based on the 2 dimensional velocity of moving targets, an equivalent parametric model is constructed to transform the moving target echo into squint SAR echo. Then, with different parameters the modified iterative thresholding algorithm is applied to achieving imagery of moving target. Finally, the motion parameters of targets are obtained by minimizing the image entropy. It is shown that, using the proposed method, the required echo sampling can be reduced, the Doppler ambiguity problem can be avoided and accurate velocity estimation can be obtained even in low signal-to-clutter ration scenarios. Simulation results verify the effectiveness of the proposed method.

SAR; Parametric model; Moving target; Parameter estimation

TN957.51

A

1009-5896(2016)12-3049-07

10.11999/JEIT160922

2016-09-12；改回日期：2016-11-11；

2016-12-13

陈一畅 cyc_2007@163.com

国家自然科学基金(61631019, 61471386)

The National Natural Science Foundation of China (61631019, 61471386)