基于三阶多项式傅里叶变换的SAR地面加速运动目标参数估计与成像

周 辉 赵凤军 杨 健



基于三阶多项式傅里叶变换的SAR地面加速运动目标参数估计与成像

周 辉*①②赵凤军①杨 健③

①(中国科学院电子学研究所 北京 100190)②(中国科学院大学 北京 100049)③(中国运载火箭技术研究院 北京 100076)

该文主要针对加速运动目标的参数估计及成像问题，推导了加速度目标的SAR回波频谱，分析了回波相位三次项估计和补偿对运动参数估计和SAR成像的必要性。提出一种利用Hough变换估计距离走动率和径向速度、相位补偿法校正距离徙动效应，并基于三阶多项式傅里叶变换(LPFT)对三次相位估计的新方法。利用Hough变换，在不明显增加计算量的前提下，达到加速运动目标的运动参数精确估计和精确聚焦成像的目的。最后通过仿真数据验证了该算法的有效性。

合成孔径雷达；地面运动目标成像；加速度估计；三阶多项式傅里叶变换；Hough变换

1 引言

地面运动目标成像技术是近年来合成孔径雷达研究中的热点问题，在对静止场景成像的同时对运动目标检测与成像在军事等领域有着重要的意义。由于存在相对载机平台的额外运动，运动目标的多普勒中心及调频率都会发生改变，在静止场景SAR图像中会呈现出方位移位和散焦等问题，不利于SAR图像应用。

由于运动目标的径向速度使其方位频谱发生多普勒中心偏移，因此对于运动目标的高分辨成像首先要进行距离徙动校正，消除径向速度对成像算法的影响。多数文献中均使用Keystone变换进行距离走动校正。然而Keystone变换虽然能达到对距离走动效应的盲校正，但其面临两个方面的问题：首先，Keystone变换需要差值运算，计算量大；其次，动目标径向速度较大时，多普勒中心出现混叠，Keystone变换失效[6,7]。

常规的运动目标成像方法都是假设运动目标在合成孔径时间内作匀速直线运动，通过对运动目标回波频谱的一次和二次相位的估计即可反演出运动目标的速度分量，进而对运动目标重新聚焦。常用的估计方法有时频分析法[8]、距离历程拟合法[9]、子孔径法[10]等等。实际情况中，运动目标的运动姿态比较复杂，由于其加速度的存在，回波频谱的三次相位影响无法忽略。

针对以上的问题，本文提出使用Hough变换对距离走动率进行估计，得到径向速度值，并根据估计出的多普勒中心通过相位补偿的方式校正距离走动和距离弯曲效应。此方法采用相位复乘避免了差值，运算量小；其次利用Hough变换估计距离走动率避免了多普勒中心混叠的影响，对于提取出的含有动目标的距离门信号进行三阶多项式傅里叶变换(LPFT)。本文具体介绍该算法的原理与各步骤的实现方法，具体安排如下：第2节推导了加速动目标的频谱并分析了三阶相位估计对运动目标运动参数估计和成像的必要性；第3节介绍了距离徙动校正的方法；第4节介绍了三阶LPFT的估计方法；第5节通过仿真数据对该算法的正确性进行了验证。

2 加速运动目标回波分析

运动目标的运动参数可以分解为径向速度、径向加速度、方位向速度及方位向加速度4个分量。在机载正侧视SAR合成孔径时间内，运动目标的回波表达式与静止目标相同，单点目标基带回波表达式可以表示为

与静止目标相比，运动目标由于自身存在相对于雷达平台的额外运动，其瞬时斜距公式与静止目标有所不同。机载SAR运动目标在斜距平面内的几何关系如图1所示，运动目标的径向速度为，径

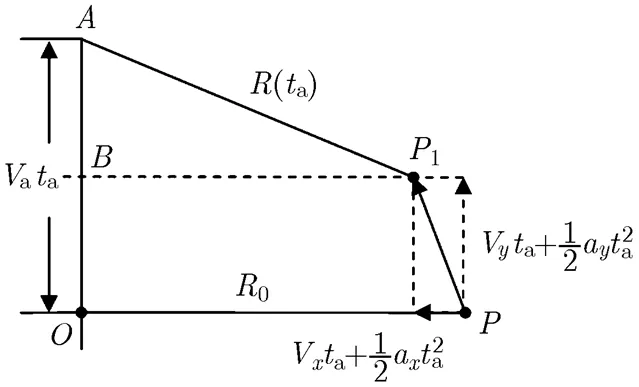
图1正侧视机载SAR运动目标几何关系图

将式(3)代入式(1)，得到距离压缩后的回波信号为

在式(4)中，第2项指数项为动目标多普勒中心偏移项；第3项指数项为方位时间二次项，运动目标由于存在方位向速度和距离项加速度，使得其调频率相对静止目标发生了变化；第4项指数项为方位时间三次项，三次项会造成压缩后旁瓣的不对称性，对成像效果有较大的影响，同时三次相位的产生与目标的径向速度、方位向速度、方位向加速度有关；第5、第6项指数项分别为距离走动项和距离弯曲项。

从目标方位谱的三次项可以看出，三次项的产生主要与径向速度、方位向速度有关。由于分母取值很大，一般在几千米至一万米之间，而方位向加速度的取值认为较小，在此可以认为方位加速度的值可以忽略，可以只考虑径向速度、径向加速度、方位向速度对于动目标频谱的影响。因此对于3个未知参数可以通过三次相位项来得到准确的估计，即

综上分析可知，通过估计方位频谱的三次相位可以得到运动目标径向速度、径向加速度、方位向速度这3个分量的准确估计。同时，当径向速度较大时，回波频谱的三次项影响不可忽略，对于三次频谱分量的补偿有助于提高动目标成像的质量。然而估计3次频谱会明显增加估计的复杂度和运算量，因此本文将在后续小节中详细介绍结合Hough变换的三阶LPFT降阶算法，在不增加参数估计运算量的前提下对运动目标的参数进行精确估计并准确聚焦。

3 运动目标的距离徙动校正

运动目标的径向速度会造成方位向频谱产生多普勒中心偏移，径向加速度和方位向速度会造成多普勒调频率改变。同时，这两项运动目标产生的相位还会使得运动目标相对于静止目标而言发生额外的距离徙动效应。

距离徙动效应可以分为距离走动效应和距离弯曲效应两部分，提取式(4)中的距离徙动项，可知

式(10)中第1项为距离走动项，第2项为距离弯曲项。其中，距离走动项使得距离压缩后的回波为一条斜线。估计此斜线的斜率就可以得到距离走动率，从而对距离走动效应进行校正，同时可以反演出目标的径向速度。对于回波距离走动率的估计可以采用Hough变换的方法完成。

Hough变换的原理如图2所示，2维平面表示距离压缩后的2维时域，运动目标的距离走动曲线为一条不平行于轴的直线。对Hough变换采用标准化参数方程为

如果忽略目标方位速度和径向加速度对于目标距离弯曲产生的影响，只考虑补偿载机运动的影响，得到的一致RCM可以表示为

根据相位驻定原理，将回波信号变换至距离频域，可知

将式(14)代入式(13)，可以得到

因此，结合式(13)中估计出的径向速度，可以作出运动目标在距离频域的距离徙动校正滤波器，其表达式为

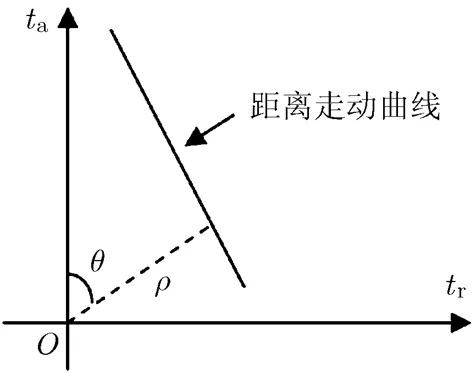
图2 Hough变换原理示意图

利用式(16)中的滤波器可以通过相位补偿的方式在距离频域将运动目标的距离徙动效应进行校正，使其能量尽可能集中在一个距离门内，从而应用LPFT方法进行参数估计。

4 多项式傅里叶变换

标准离散傅里叶变换的形式为

多项式傅里叶变换(LPFT)可以定义为

估计至二阶相位的方法在含有加速度的运动目标的运动参数反演问题上含有较大误差，且如果径向运动速度过大，三阶相位还会造成压缩后旁瓣不对称性，严重影响到动目标成像的精度。基于以上分析，本文提出利用三阶LPFT对回波相位进行估计的方法[18]。对每个距离门信号，三阶LPFT的表达式为

因此，各阶相位参数的估计值可以由式(22)得到：

然而LPFT估计高阶相位参数时面临的问题是多维参数搜索运算量较大，因此本文提出在RCMC环节中利用Hough变换估计出目标的径向速度，三阶LPFT可以降阶为只估计二阶和三阶相位参数的二阶LPFT。式(21)可以修改为

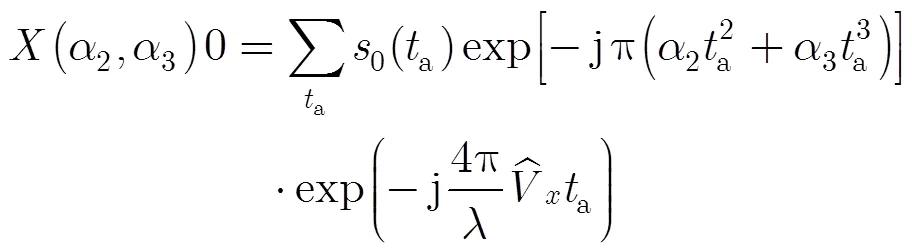
相位参数的估计公式可以表示为

(24)

由此可见，2维参数搜索可以得到动目标回波的三阶相位，运算量相比二阶LPFT没有任何提升。具体的实现步骤为：

(1) 提取出运动目标所在的距离门；

(3) 应用二次循环逐次变化二阶和三阶相位的设定参数，生成LPFT滤波器，与回波相位进行多项式傅里叶变换，并记录每次变换的最大值；

(4) 在每次变换产生的最大值中找到最大的一点作为所要搜索的峰值点，将2维峰值搜索分解为两次1维峰值搜索能够减少算法的存储量，有利于实时处理。

根据三次相位的估计值，可以得到运动目标的径向速度、方位向速度、径向加速度的反演公式为

实现加速运动目标成像的算法流程如图3所示。

如图3所示，如果场景中包含多个运动目标，可以参考基于“CLEAN”思想[19,20]的多目标处理方法，即首先提取幅值最高的动目标回波进行估计成像，得到该目标的参数并聚焦后，将该目标的回波从多动目标的总回波中去除该目标回波能量，再剩下目标中提取能量最高的目标，并重复此过程。

5 仿真结果与分析

针对加速运动目标的参数估计与成像问题，在仿真时可以通过设置静止点目标来模拟静止地物回波，在此回波内叠加含有速度与加速度的运动点目标。仿真参数如表1所示。

表1 仿真实验基本参数

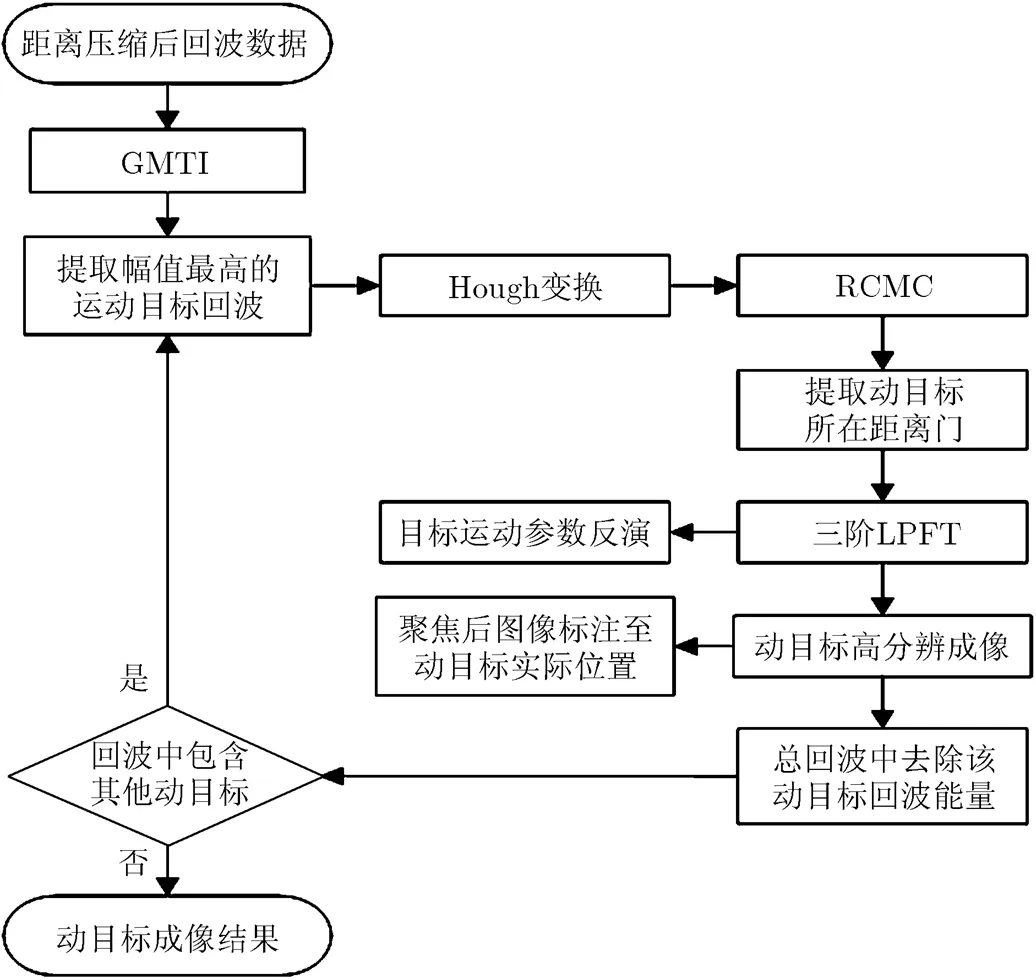
图3 基于三阶LPFT的加速动目标成像算法流程图

在仿真中，将运动目标设置在场景中心，静止目标与动目标在同一方位门，但是其与载机的斜距大于运动目标100 m，从而与运动目标进行区分。图4(a)为距离压缩后的运动目标与静止目标的图像，由于径向速度的影响，运动目标距离压缩曲线出现了距离走动效应；图4(b)为聚焦成像后的运动目标和静止目标图像，运动目标由于径向加速度和方位向速度的影响，其成像在静止目标图像中出现散焦，同时，由于径向速度的影响，动目标在图像位置中出现了方位向错位现象，由于本仿真中径向速度较大，所以方位向错位还出现了方位混叠。

提取出运动目标的回波后，利用Hough变换估计该距离徙动曲线的斜率，并在距离频域与RCMC滤波器相乘，补偿掉方位距离耦合相位。利用距离频域补偿法校正后的动目标距离压缩曲线如图5所示。其中图5(a)为提取出的运动目标频谱；图5(b)为RCMC后的距离压缩曲线，该方法能够将距离走动精确校正，运动目标能量已经集中在其所在距离门内。

为了对比常规的时频分析法及三阶LPFT算法对运动目标成像及参数估计的性能，在仿真中使用常用的分数阶傅里叶变换(FrFT)对该运动目标的参数进行估计，与本文提出的三阶LPFT算法效果进行比较[15]。图6(a)为根据分数阶傅里叶变换估计出的二阶相位对动目标成像后的图像，图6(b)为根据三阶LPFT估计出的二阶及三阶相位对运动目标成像后的图像。从图6的对比中可以看出，图6(a)中目标在方位向的旁瓣出现不均匀的现象，而图6(b)中旁瓣对称，压缩效果较好，回波中高次相位得到了很好的补偿。图7为FrFT算法与三阶LPFT法估计后运动目标方位向剖面dB图，从图7中可以更加清楚看出三阶LPFT算法在运动目标成像上的优越性。

运动目标成像效果的数值性能指标如表2所示。从表2中看出，三阶LPFT的成像效果无论是从峰值旁瓣比还是积分旁瓣比上性能都优于传统方法。

表2 FrFT算法与三阶LPFT算法的成像性能指标(加窗)

根据第4节中运动目标运动参数的反演式(27)~式(29)，将Hough变换的估计参数，三阶LPFT的估计参数，以及反演出的运动参数列于表3。

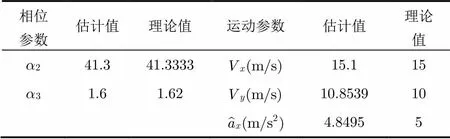
表3 三阶LPFT估计结果及运动参数反演

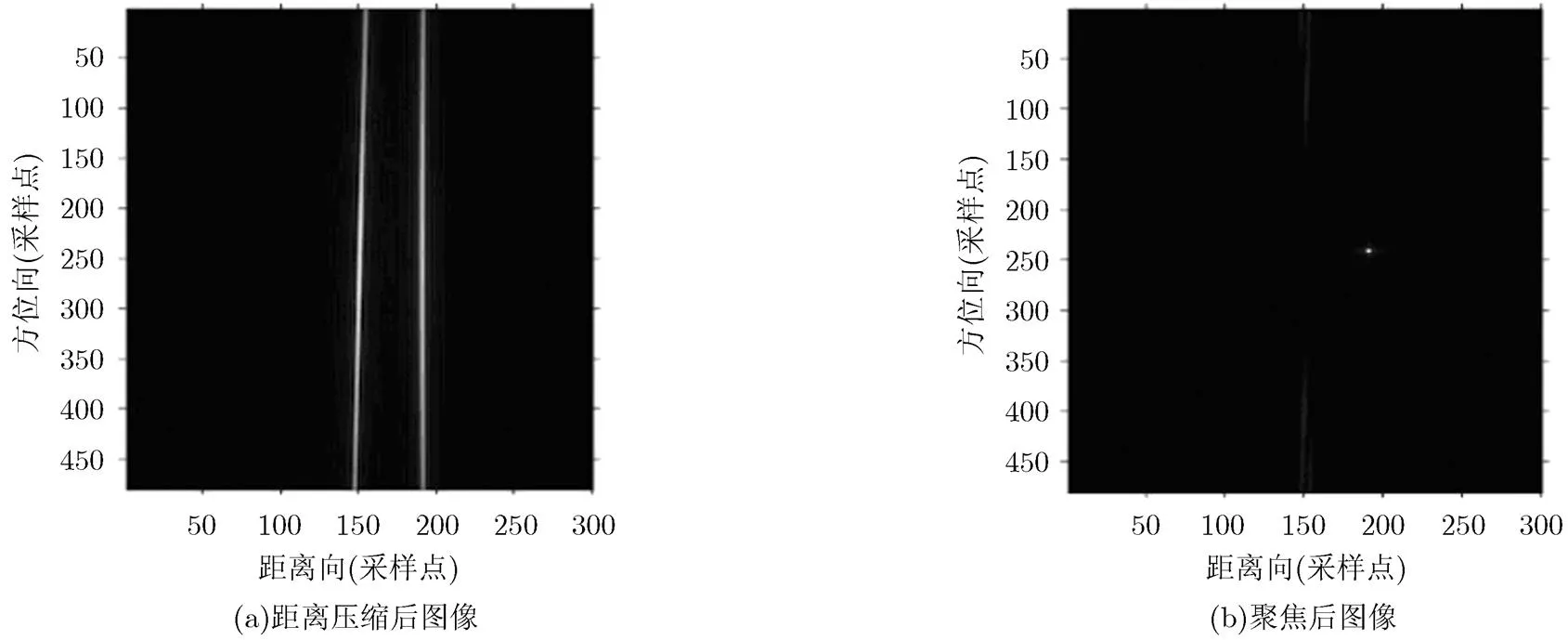
图4 运动目标在静止地物中图像

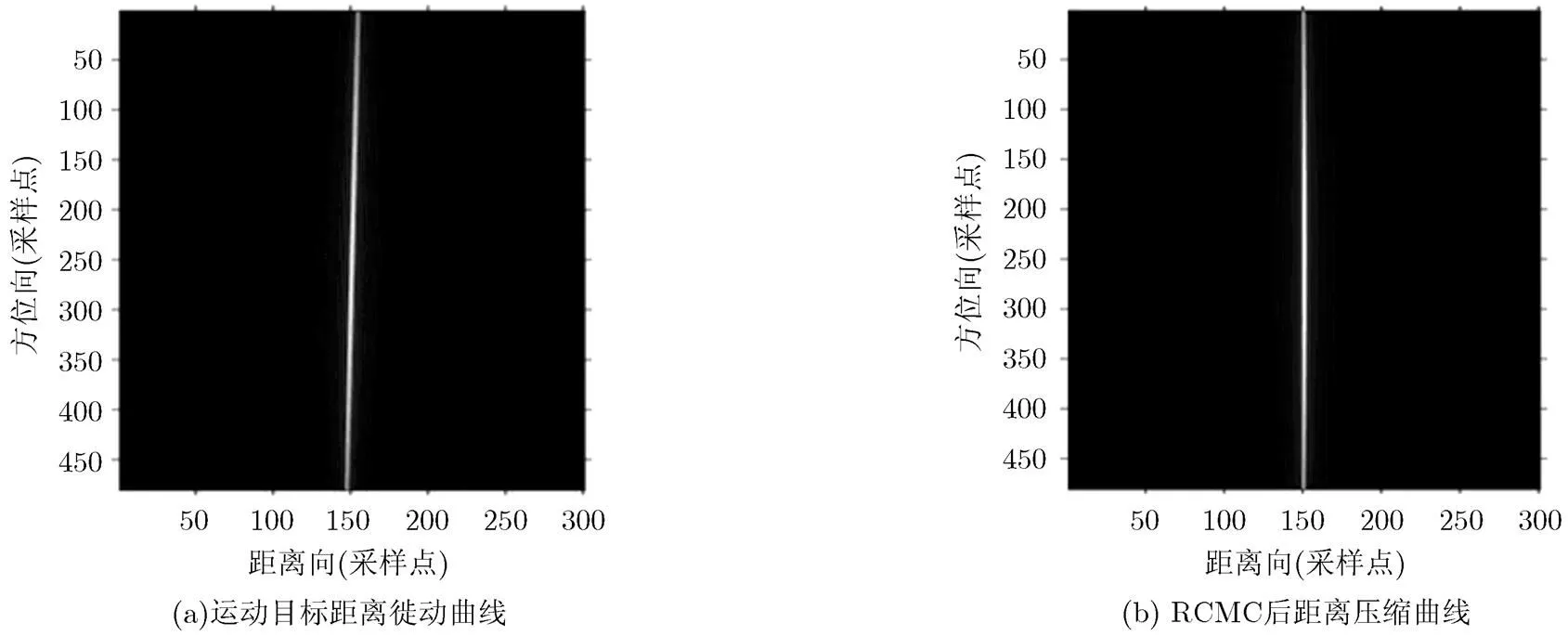
图5 运动目标RCMC前后对比图像

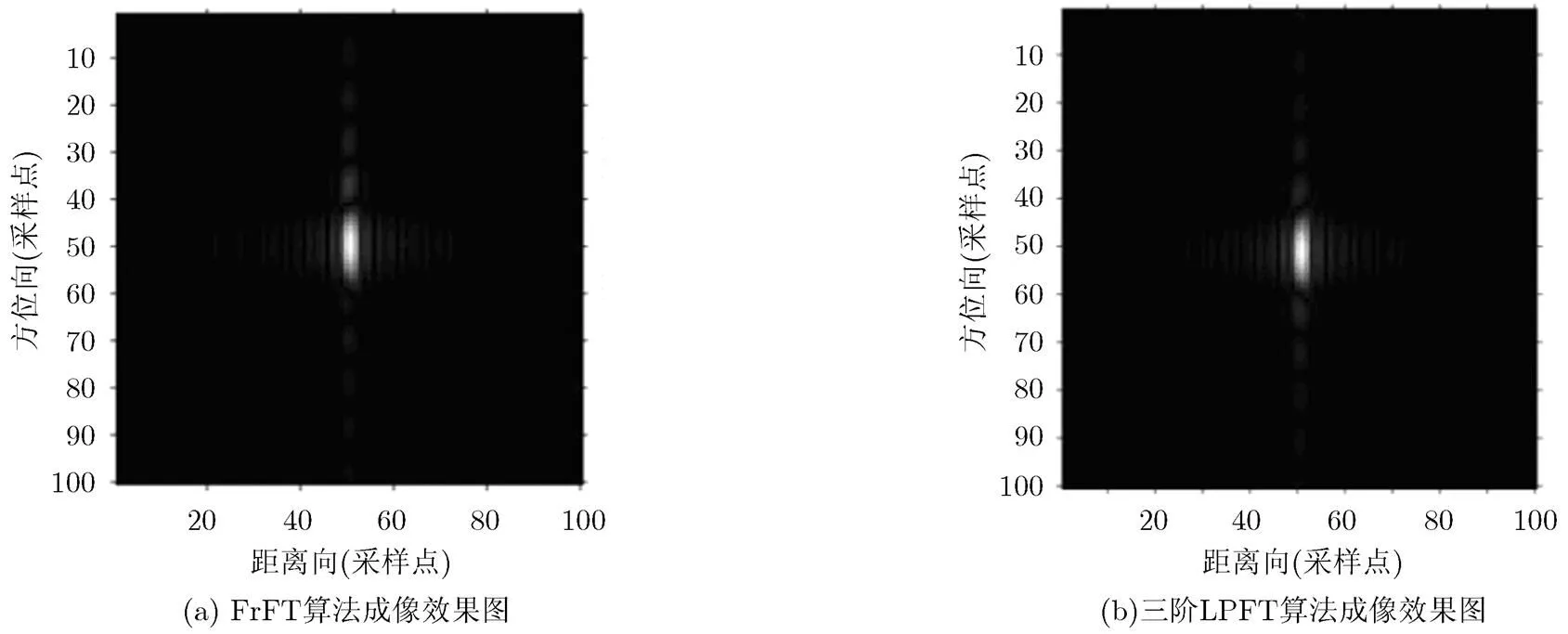
图6 FrFT与三阶LPFT算法估计参数成像效果对比图(截取目标区域)

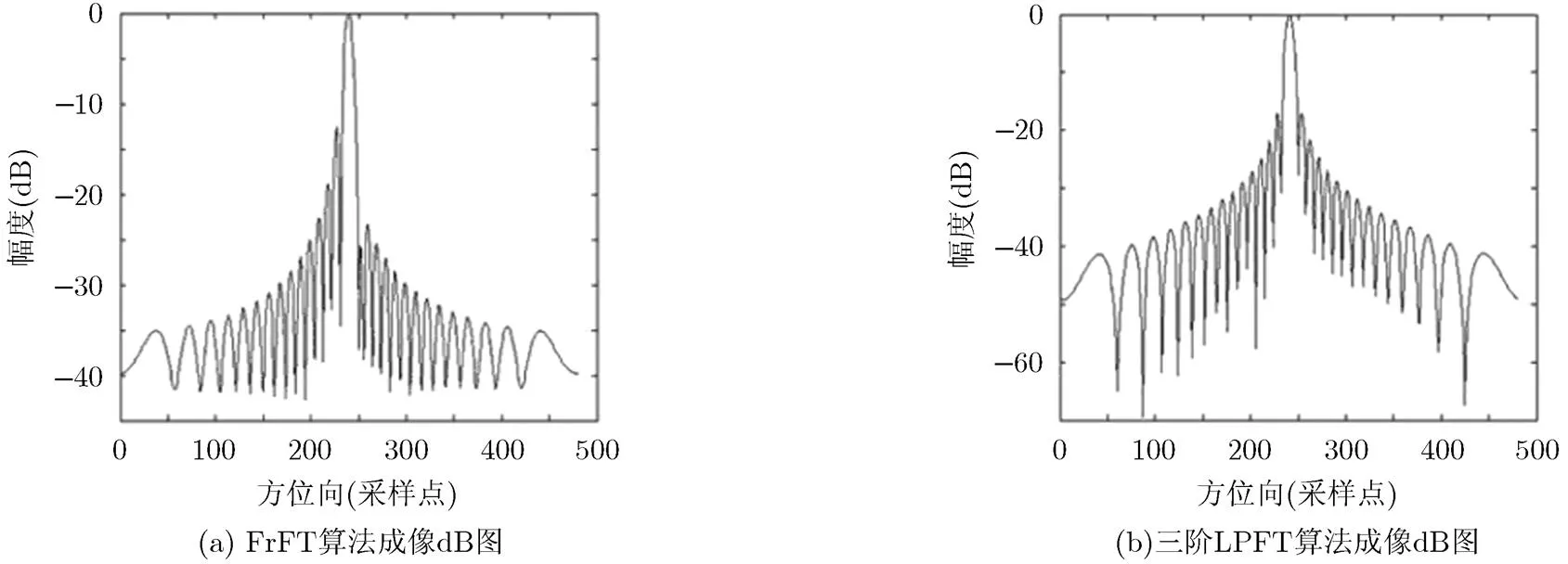
图7 FrFT与三阶LPFT算法估计参数成像dB图

从表3中看出，应用本文方法对于加速运动目标的运动参数的估计基本是准确的。

6 结束语

本文首先分析了运动目标的三次回波表达式，并提出了一种新的运动目标成像算法。即首先利用Hough变换估计运动目标距离徙动曲线的斜率，采用这一方法在避免了多普勒中心模糊问题的同时，可以得到目标径向速度的估计值。然后，利用估计出的斜率在距离频域通过相位复乘的方式补偿RCM相位。提取出目标所在距离门后，利用本文提出的三阶LPFT法对目标的相位参数进行估计，通过结合Hough变换估计出的一次相位参数，三阶LPFT搜索可以在2维参数平面内进行，从而在不显著提高运算量的前提下精确估计出运动目标的相位参数和运动参数，最终对运动目标高分辨成像并标注在实际位置上。在仿真实验中，通过与分数阶傅里叶变换结果的对比，分析验证了本文算法的有效性。

[1] ZHOU Feng, XING Mengdao, and BAO Zheng. Approach for single channel SAR ground moving target imaging and motion parameter estimation[J].,&, 2007, 1(1): 59-66.

[2] SUN Guangcai, XING Mengdao, XIA Xianggen ,Robust ground moving-target imaging using deramp– keystone processing[J]., 2013, 51(2): 966-981.

[3] YANG J, LIU C, and WANG Y F. Imaging and parameter estimation of fast-moving targets with single-antenna SAR[J]., 2014, 11(2): 529-533.

[4] YANG J G, HUANG X T, JIN T,New approach for SAR imaging of ground moving targets based on a keystone transform[J]., 2011, 8(4): 829-833.

[5] 汤立波, 李道京, 吴一戎, 等. 机载SAR的地面运动目标成像处理[J]. 系统工程与电子技术, 2005, 27(10): 1681-1686.

TANG Libo, LI Daojing, WU Yirong,Imaging of ground moving targets based on airborne SAR[J]., 2005, 27(10): 1681-1686.

[6] CAO Yufei, QU Xiaoguang, and HUANG Peikang. Research on keystone formatting based on non-baseband interpolation [J]., 2010, 21(4): 562-565.

[7] 朱圣棋, 廖桂生, 曲毅, 等. 机载正侧视合成孔径雷达地面运动目标参数估计方法[J]. 电子学报, 2010, 38(12): 2757-2762.

ZHU Shengqi, LIAO Guisheng, QU Yi,An approach of ground moving target motion parameter estimation for airborne side looking SAR system[J]., 2010, 38(12): 2757-2762.

[8] YANG Jungang, HUANG Xiaotao, JIN Tian,New approach for SAR imaging of ground moving targets based on a keystone transform[J]., 2011, 8(4): 829-833.

[9] 盛蔚, 毛士艺. 地面多个运动目标成像及定位问题的研究[J]. 系统工程与电子技术, 2003, 25(9): 1074-1078.

SHENG Wei and MAO Shiyi. Research on the imaging and location for multiple ground moving targets[J]., 2003, 25(9): 1074-1078.

[10] 康雪艳, 杨汝良. 一种有效的机载合成孔径雷达动目标成像方法[J]. 测试技术学报, 2004, 18(3): 214-218.

KANG Xueyan and YANG Ruliang. An effective imaging method of moving targets in airborne SAR real data[J]., 2004, 18(3): 214-218.

[11] KATKOVNIK V. A new form of the Fourier transform for time-frequency estimation[J]., 1995, 47 (2): 187-200.

[12] DJUROVIC I , THAYAPARAN T, and STANKOVIC L. SAR imaging of moving targets using polynomial Fourier transform[J]., 2008, 2(3): 237-246.

[13] QU Changwen, HE You, SU Feng,SAR moving targets detection based on the chirp-Fourier transform[C]. IEEE International Radar Conference, Arlington, 2005: 802-805.

[14] STANKOVIC LJUBISA and DJUKANOVIC Slobodan. Order adaptive local polynomial FT based interference rejection in spread spectrum communication systems[J]., 2005, 54(6): 2156-2162.

[15] 刘颖, 陈殿仁, 陈磊, 等. 基于周期Choi-Williams Hough变换的线性调频连续波信号参数估计算法[J]. 电子与信息学报, 2015, 37(5): 1135-1140. doi: 10.11999/JEIT140876.

LIU Ying, CHEN Dianren, CHEN Lei,. Parameters estimation algorithm of linear frequency modulated continuous wave signals based on period Choi-Williams Hough transform[J].&, 2015, 37(5): 1135-1140. doi: 10.11999/ JEIT140876.

[16] 刘建成, 王雪松, 肖顺平, 等. 基于Wigner-Hough变换的径向加速度估计[J]. 电子学报, 2005, 33(12): 2236-2238.

LIU Jiancheng, WANG Xuesong, XIAO Shunping,. Radial Acceleration Estimation Based on Wigner-Hough Transform [J]., 2005, 33(12): 2236-2238.

[17] 问翔, 刘宏伟, 包敏. 一种距离扩展目标的Hough变换检测器[J]. 电子与信息学报, 2015, 37(5): 1104-1110. doi: 10.11999/ JEIT140692.

WEN Xiang, LIU Hongwei, and BAO Min. A Hough transformation detector for range spread target[J].&, 2015, 37(5): 1104-1110. doi: 10.11999/JEIT140692.

[18] 阮航, 吴彦鸿, 叶伟. 基于FRFT-CLEAN的机动目标逆合成孔径激光雷达成像算法[J]. 电子与信息学报, 2013, 35(7): 1540-1546. doi: 10.3724/SP.J.1146.2012.01423.

RUAN Hang, WU Yanhong, and YE Wei. Inverse Synthetic aperture radar imaging algorithm for maneuvering target based on FRFT-CLEAN[J].&, 2013, 35(7): 1540-1546. doi: 10.3724/SP.J.1146.2012.01423.

[19] YANG Jian, LIU Chang, and WANG Yanfei. Detection and imaging of ground moving targets with real SAR data [J]., 2015, 53(2): 920-923.

[20] 周辉, 赵凤军, 禹卫东, 等. 基于非理想运动误差补偿的SAR地面运动目标成像[J]. 雷达学报, 2015, 4(3): 265-275.

ZHOU Hui, ZHAO Fengjun, YU Weidong,. SAR imaging of ground moving targets with non-ideal motion error compensation[J]., 2015, 4(3): 265-275.

周 辉： 男，1982年生，博士生，研究方向为SAR运动目标检测及成像处理.

赵凤军： 男，1963年生，研究员，博士生导师，研究方向为星载SAR系统设计.

杨 健： 男，1982年生，博士，工程师，研究方向为SAR运动目标检测及成像处理.

SAR Accelerating Moving Target Parameter Estimation and ImagingBased on Three-order Polynomial Fourier Transform

ZHOU Hui①②ZHAO Fengjun①YANG Jian③

①(Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)②(University of Chinese Academy of Sciences, Beijing 100049, China)③(China Academy of Launch Vehicle Technology, Beijing 100076, China)

This paper aims at the issue of accelerating moving target parameter estimation and imaging. The SAR echo spectrum of target with acceleration is calculated, and the necessity of estimation and compensation of the three-order moving target echo phase to imaging and movement parameter estimation is analyzed. Then, a Novel algorithm is proposed to estimate range cell migration rate and range velocity by Hough transform, compensate the range cell migration by phase compensation, and estimate the three-order phase using three-order Local Polynomial Fourier Transform (LPFT). Using the parameter estimated by Hough transform, the movement parameters can be precisely estimated and image well focused without increasing the calculation significantly. Simulated data processing results are provided to demonstrate the effectiveness of the proposed algorithm.

SAR; Ground Moving Target Imaging(GMTIm); Acceleration estimation; Three-order Local Polynomial Fourier Transform (LPFT); Hough transform

TN958

A

1009-5896(2016)04-0919-08

10.11999/JEIT150679

2015-06-04；改回日期：2015-10-09；网络出版：2015-11-19

周辉 zhouh@chinastns.com