基于Amdahl定律的多核密码处理器性能模型研究

冯 晓 戴紫彬 李 伟② 蔡路亭



基于Amdahl定律的多核密码处理器性能模型研究

冯 晓①戴紫彬①李 伟*①②蔡路亭①

①(解放军信息工程大学 郑州 450000)②(复旦大学专用集成电路与系统国家重点实验室 上海 201203)

该文构建面向密码应用的多核处理器性能模型，对多核密码处理器设计提供理论支持和有效建议。通过引入密码并行处理特征、数据传输时间、同步时间等因素，建立基于Amdahl定律扩展的多核密码处理器性能模型，基于提出的性能模型，对多核密码处理器设计空间进行搜索。

密码处理器；多核处理器；Amdahl定律；性能模型；通信/计算比

1 引言

密码算法作为保证信息安全的重要措施，在整个信息系统中占有非常重要的地位。密码处理器具有密码专用指令及相应的密码专用运算单元，能够高效灵活地实现密码处理任务，成为实现密码算法的主要方式之一[1]。然而，随着信息网络的飞速发展，对密码处理器性能提出了更高的要求，而受限于功耗、线延时、设计复杂度等因素，依赖于传统的单核架构提升密码处理性能变得越来越困难[2]。

相对于传统单核处理器，多核处理器可以提供更强的处理能力，成为许多高性能计算平台的首选解决方案。结合多核处理器设计技术和密码处理器技术，设计面向高速密码应用的多核密码处理器，不仅能够有效满足信息安全领域日益增长的需求，同时也具有创新性和理论研究价值。然而，目前面向高速密码应用的多核密码处理器研究尚处于起步阶段，理论体系尚不完备。本文拟基于并行系统加速比定律Amdahl定律，结合密码并行处理特征、处理器规模、通信消耗等性能因素对定律进行扩展，通过建模及参数分析，构建多核密码处理器性能模型，为多核密码处理器结构设计提供一定的理论支持和建议。

2 Amdahl定律研究

Amdahl定律由IBM大型机之父Amdahl博士在1967年首次进行描述[6]。Amdahl指出系统采用并行化技术后所能获得的性能提升受限于系统中并行化部分所占比例。该论述在并行计算领域得到充分肯定和广泛应用[7]，逐渐成为描述并行系统加速比的基本定律，Amdahl定律可抽象为

国内外提出了许多基于Amdahl定律的多核处理器性能模型。文献[8]定义了算法中的关键程序段(critical section)，充分考虑并行进程通过关键程序段的同步问题，并指出同步问题是影响多核系统性能的关键因素之一。文献[9]将通信开销引入到Amdahl定律中，提出了关于层次化片上多核处理器的Amdahl定律扩展。文献[10]将程序的并行度引入到Amdahl定律中，建立了多级并行计算(multi- level parallel)的加速比模型，该模型假定了并行度对通信开销没有影响，虽然指出了处理器数目会对算法可执行并行度有影响，但是未对其做进一步研究，模型精确度有待提高。文献[11]建立了面积-性能模型，用于评估处理器规模受限时可达到的最高性能。文献[12]将通信开销引入Amdahl定律，建立了基于面向广域分布式系统通信特征的多核性能模型。文献[13]将算法分解为多个部分，每部分可以以不同比例进行加速。文献[14]充分讨论了核间通信时间及并行串行部分的数据同步时间对多核系统性能影响并对Amdahl定律进行了修正。文献[15]基于任务并行特征建立了进程级封闭式排队网络模型(thread-level closed-queuing network model)，用于评估多进程多核处理器的并行计算能力

Amdahl定律中有3个假设：(1)应用程序中只存在一种可开发并行度；(2)无论应用程序中的可并行部分并行度多大，系统都能够实现；(3)应用程序并行化实现不会引入额外的通信开销。然而在实际应用中，这3点假设是不准确的。为更精确地评估系统性能，需将以上3点补充进Amdahl定律。目前，尚无综合考虑以上3种因素的多核处理器性能模型[16]。针对上述不足，本文将密码算法并行特征、处理器规模、数据传输时间、同步时间等因素引入Amdahl定律，建立基于Amdahl定律的多核密码处理器性能模型。

3 基于Amdahl定律扩展的多核密码处理器性能模型

3.1 多核密码处理器性能模型

多核处理器一般采用已有的成熟的单核处理器作为计算核心，本文研究基于成熟的密码处理器(单核)，为简化研究复杂度，计算核心为相同的密码处理器，即研究对象为同构多核密码处理器结构。设同构多核密码处理器共个核，借鉴等价基本核模型，每个核抽象为等价的基本核BCE(Base Core Equivalents)[17]，BCE通过某种互连方式连接为一个系统。设多核处理器BCE数目为，单个BCE单位时间内可完成的运算量为，下面根据Amdahl定律，分析多核密码处理器性能，构建多核密码处理器性能模型。

(1)并行比例及并行度： 密码算法可分解为串行执行部分及多种并行度的并行执行部分。如图1(a)所示为某密码程序段执行顺序的分解图，由图中可知，该段程序有串行执行部分及并行度分别为2, 3, 4, 5的并行执行部分。将图1(a)程序中相同并行度的任务组合在一起，则该密码程序段可重新分解为如图1(b)所示结构，分别表示密码程序中并行度为5, 4, 3, 2和1的部分。

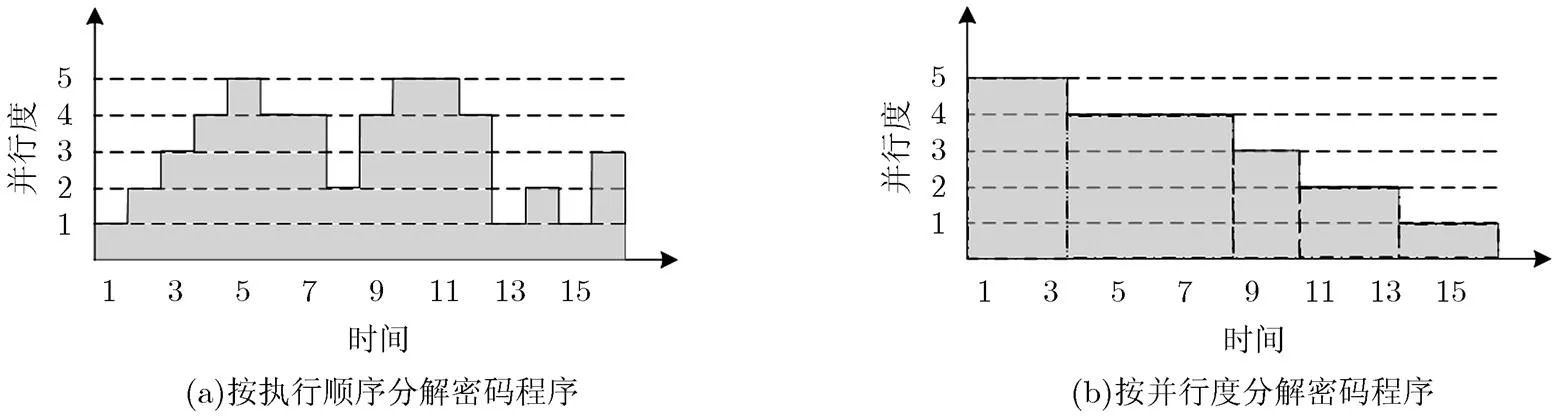
图1 密码程序分解图

密码处理器主要面向具有某种特征的一类算法，由于密码算法的差异性，密码处理器类型呈现多样化特征。而并行度是一个相对量，可消除这些差异性带来的影响。通过引入并行度参数不仅能够提高模型准确度，还能够扩展性能模型的适用范围。

(2)可实现并行度： 多核密码处理器系统不可能集成无限多个密码处理核心，当时，多核处理器完成工作量的时间；当时，最快只能以并行度完成。因此，多核处理器完成工作量的时间为

通信开销： 并行计算中BCE间会有通信开销，主要包括数据传输时间和数据同步时间。

应用程序中通信量与计算量有关[18]，密码程序中计算量较为固定，设密码程序通信计算比为，则多核处理器完成计算量所需通信量为。单位时间内数据传输量是与多核处理器拓扑结构有关的函数，设核处理器单位时间内可传输数据量为，则完成并行度任务所需数据传输时间：

并行计算中，数据同步直接决定了整体计算结果的正确与否。设设并行度为时通信次数为，同步机制每次通信的同步开销为，则完成所需的同步时间为有

基于以上分析，多核密码处理器完成任务W所需时间，可用式(7)表示：

3.2 多核密码处理器性能模型参数分析

密码算法特点是数据运算比较整齐，算法内并行度变化较少，并行度一般为=1, 2, 4, 8，例如AES轮运算并行度取值为1或4(S盒可开发=16并行度)，DES轮运算并行度取值为1或8, IDEA轮运算并行度取值为1或4, MD5轮运算并行度取值为1或4, A5算法中移位寄存器次态信息受其前一状态控制，其并行度为1。

以密码协议方式处理数据分组，各个密码算法间可实现并行，可开发并行度与协议所包含的密码算法数目相等。如SSL(Secure Sockets Layer)协议中包括非对称加密、对称加密、单项杂凑3个步骤，3个步骤可通过流水方式并行执行，可开发并行度为3。

操作模式主要有ECB(Electronic CodeBook)，CBC(Cipher Block Chaining), CFB(Cipher FeedBack), OFB(Output FeedBack)和CTR (CounTer Mode)等。除ECB工作模式外，其余工作模式中都是反馈工作模式，存在很强的数据相关，开发并行性难度很大。由于安全原因，ECB模式极少使用，因此数据包内各个分组间的可开发并行度有限。

不同数据包间一般不存在数据相关，理论上存在无限大的可开发并行度。

以2D-Mesh结构为例，在常规2D-Mesh结构中，消息的平均跳步数为[9]，消息经过每个互连节点延迟一个时钟周期。由于吞吐率要求，目前设计的密码处理器中，密码算法程序执行时间一般控制在102~103数量级的运算周期，若互连网络的位宽为32 bit，一次可传输1~32个数据，代入式(8)可得

以AES为例，若不采用并行结构，即=1，此时=0，多核密码处理器BCE间无通信；若采用密钥生成部分与轮运算部分并行的结构，即=2，多核密码处理BCE间有通信，且通信次数为1，通信量等于密钥长度；若轮运算部分采用4核并行，即=4，多核BCE间有通信且通信量每轮为128 bit，每轮通信3次，完成轮运算需通信36次。可见，由于算法和映射方式的不同，通信计算比及通信次数变化较大，当密码算法及算法映射固定时，通信计算比及通信次数固定。在第4节设计空间搜索中，为尽量覆盖算法映射情况，通信计算比及通信次数尽量设计变化较大的取值范围。

4 多核密码处理器设计空间搜索

本节将基于第3节多核密码处理器性能模型参数的分析结果，对多核密码处理器设计空间进行搜索，分析其设计原则并给出设计建议。

设单个BCE完成任务所需时间为单位1。首先，分析通信性能对多核密码处理器性能的影响。将(假设只存在1, 2, 4, 8, 16并行度，且各部分所占比例相同)，(设为0.01)，,(设为)等参数固定，模拟不同取值下，多核密码处理器性能与BCE数目的关系。如图2所示，横坐标表示多核密码处理器BCE数目，纵坐标表示多核密码处理器运算时间。

由图2中可以发现，6条曲线基本重合，可见，对于多核密码处理器，BCE互连结构对多核密码处理器的性能影响并不大。 同时，由曲线趋势可以发现，在BCE数目为2, 4和8时，多核密码处理器性能提升幅度较大，而当BCE数目大于8时，处理器性能提升很少。可见，多核密码处理器性能并非随BCE数目增加而增加。

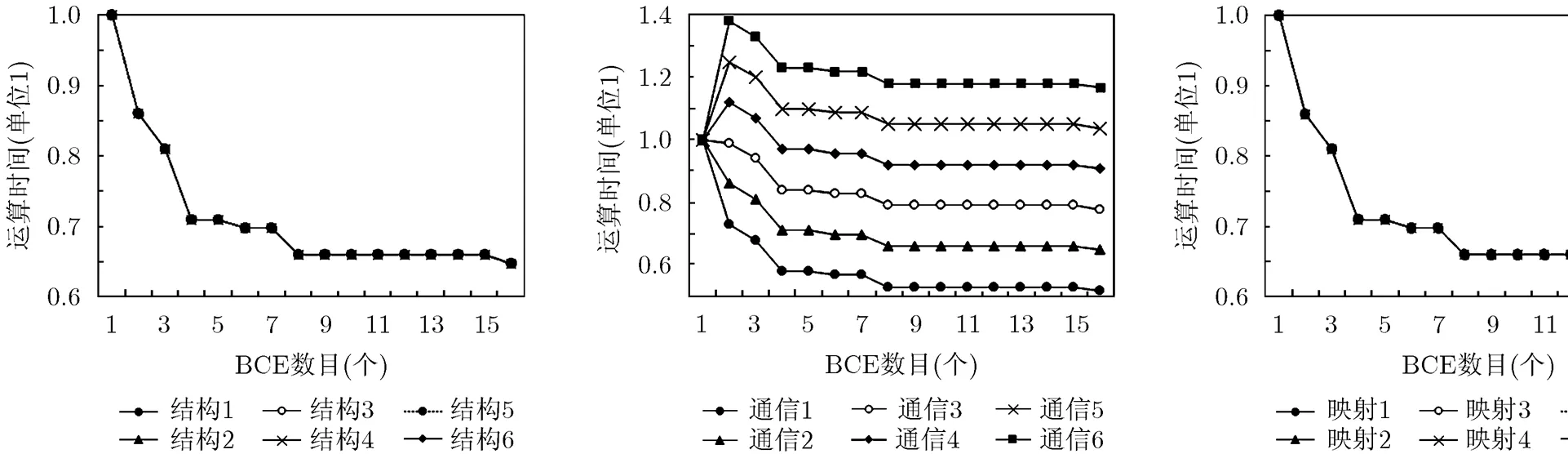
图2 对多核密码处理器性能影响 图3 对多核密码处理器性能影响 图4 对多核密码处理器性能影响

图5 对多核密码处理器性能影响

1和4，任务计算量比例由1:1递减到1:6。图5(c)为密码应用场景3，密码应用中可开发并行度为1和8，任务计算量比例由1:1递减到1:6。图5(d)为密码应用场景4，密码应用可开发并行度为16。

分别观察图5(a)~图5(c)，可以看出，多核密码处理器结构相同时，密码程序并行部分比例越大，完成密码运算所需时间越少。如图5(a)中，BCE数目相同情况下，密码程序串行并行部分比例为1:6(比例6)时，多核处理器运算时间明显小于串行并行比例为1:1(比例1)时。同时，当多核密码处理器集成的BCE数目超过密码程序中的最大并行度后，BCE数目增加不会提高密码处理器性能。如当图5(a)中BCE数目大于2、图5(b)中BCE数目大于4及图5(c)中BCE数目大于8时，提高BCE数目并不能减少多核密码处理器完成运算任务的时间。可以得出结论，多核密码处理器可达到的最高性能主要是由密码算法可开发并行度及并行部分所占比例决定的。

图5(d)中密码应用无串行部分，用于模拟密码算法数据包级并行的情况。由图中可以看出，虽然多核密码处理器运算时间随着BCE数目增多而逐渐降低，但其下降趋势逐渐平缓，图中虚线为其拟合函数。可见，即使对于理论上可以无限并行的密码算法，多核密码处理器集成的BCE数目也并非越多越好。

通过以上设计空间搜索可得出多核密码处理器的基本设计原则：根据并行度及各并行度所占比例，确定集成的处理器数目(BCE)，算法映射中尽量减少核间通信次数。文献[8]从软件设计方面提出了关键程序部分对系统性能的影响，但未将关键程序段与硬件设计进行对应，也未对关键程序部分进行深入研究。本文则对关键部分进行了更深入的分析，指出了通信次数是影响性能的关键因素之一。文献[9]深入研究了不同层次片上数据通信延迟对多核处理器性能的影响，提出层次化设计的多核处理器具有更好的性能，本文从通信特点角度出发得出了相同的结论。文献[10]主要修订了应用程序具有多级并行度时的Amdahl定律，模型中做了大量理想化假设，并略去了通信因素的影响，与实际情况具有一定偏差。文献[11]提出的模型中，假设应用程序的并行度随着处理器核心数成一定比例关系()，实质上这是对通信开销等的简化处理，本文的研究更深入，更有说服力。文献[13]提出了程序分段加速的思想，将程序分解为多个独立加速的部分，其分段原则较为模糊，本文是按照并行度对待完成任务进行分解。文献[14]以FFT等3种典型应用为例，深入分析了通信开销对多核处理器性能的影响，并未探讨密码类应用的通信特点。文献[15]基于排队论建立了多进程多核处理器的性能模型，该模型主要用于研究多进程多核处理器可实现的最高加速比，探讨了不同同步类型及不同通信特征应用下多进程多核处理器性能随处理器数目的变化特征，该论文对应用特征等参数的提取并非基于实际应用。 此外，上述论文都忽略了应用程序可实现并行度对多核密码处理器设计的重要影响。

对比于其他基于Amdahl 定律的多核处理器性能模型，可以发现，由于引入了更完备的参数，并且在设计空间搜索时参数选取了更为贴近实际情况的取值范围，本文提出的模型对影响性能的关键因素得出了不同的结论，能够对多核密码处理器设计提供更准确的指导意见。不同与其他模型偏重于理论性，本文实现了理论性与应用性的统一。

5 结束语

多核密码处理器是未来密码处理器的发展方向，然而，目前对多核密码处理器研究的理论还不完善。在现有Amdahl定律及扩展的研究基础上，本文建立了面向密码应用的多核密码处理器性能模型，并对影响多核密码处理器处理性能的参数行了详细分析。通过对各个参数的模拟得出，多核密码处理器适用于可开发并行度高且并行部分比例大的密码应用。对于多核密码处理器，互连结构及通信计算比对处理器性能的影响较小，通信次数对多核密码处理器性能的影响较大，而多核密码处理器可到达的最高性能及对应的BCE数目主要由密码算法取值决定。

密码算法不同并行层次的操作特点不同。算法内各操作的数据相关性较大，具有较大的取值；密码协议中，各算法间一般仅需传递密码运算结果，取值较小；数据包及任务间并行，存在并行性的各个分组/任务间一般无数据相关，取值基本为0。若充分发挥多核密码处理器优势，必须充分发掘密码应用的并行性，减少各运算部分的通信次数，依据不同并行层次的通信特征，优化密码应用多核映射方案。

[1] BOSSUET L, GRAND M, GASPAR L,. Architectures of flexible symmetric key crypto engines-a survey: from hardware coprocessor to multi-crypto-processor system on chip[J].(), 2013, 45(4): 1-32. doi: 10.1145/2501654.2501655.

[2] 冯晓静. 面向服务的异构多核片上系统的关键技术研究及实现[D]. [博士论文], 中国科学技术大学, 2013.

FENG Xiaojing. Study and implementation of service oriented heterogeneous multi processor system-on-chip[D]. [Ph.D. dissertation], University of Science and Technology of China, 2013.

[3] 蒋骁辰, 李国平, 王国中, 等. 基于AVS+实时编码的多核并行视频编码算法[J]. 电子与信息学报, 2014, 36(4): 810-816. doi: 10.3724/SP.J.1146.2013.00845.

JIANG Xiaochen, LI Guoping, WANG Guozhong,. Multi-core parallel video coding algorithm based on AVS+real-time encoding[J].&, 2014, 36(4): 810-816. doi: 10.3724/ SP.J. 1146.2013.00845.

[4] SHUKLA S K, MURTHY C N S, and Chande P K. A Survey of Approaches used in Parallel Architectures and Multi-core Processors, for Performance Improvement[M]. Switzerland, Springer International Publishing, 2015: 537-545.

[5] SILBERSTEIN M. GPUs: High-performance accelerators for parallel applications: the multicore transformation (ubiquity symposium)[J]., 2014, 2014: 1-13. doi: 10.1145/ 2618401.

[6] AMDAHL G M. Validity of the single processor approach to achieving large scale computing capabilities[C]. Proceedings of Spring Joint Computer Conference, New York, 1967: 483-485.

[7] 刘斌, 赵银亮, 韩博, 等. 基于性能预测的推测多线程循环选择方法[J]. 电子与信息学报, 2014, 36(11): 2768-2774. doi: 10.3724/SP.J.1146.2013.01879.

LIU Bin, ZHAO Yinliang, HAO Bo,. A loop selection approach based on performance prediction of speculative multithreading[J].&, 2014, 36 (11): 2768-2774. doi: 10.3724/SP.J.1146. 2013.01879.

[8] EYERMAN S and EECKHOUT L. Modeling critical sections in Amdahl's law and its implications for multicore design[C]. ACM SIGARCH Computer Architecture News, New York, 2010: 362-370.

[9] 陈书明, 陈胜刚, 尹亚明. Amdahl 定律在层次化片上多核处理器中的扩展[J]. 计算机研究与发展, 2012, 49(1): 83-92.

CHEN Shuming, CHEN Shenggang, and YIN Yaming. Revisting Amdahl’s law in the hierarchical chip multicore processors[J]., 2012, 49(1): 83-92.

[10] TANG S, LEE B S, and HE B. Speedup for multi-Level parallel computing[C]. Parallel and Distributed Processing Symposium Workshops & PhD Forum (IPDPSW), Shanghai, 2012: 537-546.

[11] JUURLINK B H H and MEENDERINCK C H. Amdahl's law for predicting the future of multicores considered harmful[J]., 2012, 40(2): 1-9. doi: 10.1145/2234336.2234338.

[12] KHANYILE N P, TAPAMO J R, and DUBE E. An analytic model for predicting the performance of distributed applications on multicore clusters[J]., 2012, 39(3): 312-320.

[13] CASSIDY A S and ANDEROU A G. Beyond Amdahl's law: an objective function that links multiprocessor performance gains to delay and energy[J]., 2012, 61(8): 1110-1126. doi: 10.1109/TC.2011. 169.

[14] YAVITS L, MORAD A, and GINOSAR R. The effect of communication and synchronization on Amdahl’s law in multicore systems[J]., 2014, 40(1): 1-16. doi: 10.1016/j.parco.2013.11.001.

[15] CHE H and NGUYEN M. Amdahl’s law for multithreaded multicore processors[J]., 2014, 74(10): 3056-3069. doi: 10.1016/j.jpdc. 2014.06.012.

[16] AL-BABTAIN B M, AL-KANDERI F J, Al-Fahad M F,. A survey on Amdahl's law extension in multicore architectures[J].(), 2013, 3(3): 30-46.

[17] HILL M D and MARTY M R. Amdahl's Law in the Multicore Era[J]., 2008, 41(7): 33-38. doi: 10.1109/MC.2008. 209.

[18] ASANOVI´C K, BODIK R, CATANZARO B C,. The landscape of parallel computing research: A view from Berkeley[R]. Technical Report ofComputer Sciences University of California at Berkeley, Berkeley: UC Berkeley, 2006: 8-11.

[19] BUCHTY R, HEINTAE N, and OLIVA D. Cryptonite-A Programmable Crypto Processor Architecture for High- bandwidth Applications[M]. Berlin Heidelberg Springer, 2004: 184-198.

[20] 徐卫志, 宋风龙, 刘志勇, 等. 众核处理器片上同步机制和评估方法研究[J]. 计算机学报, 2010, 33(10): 1777-1787. doi: 10.3724/SP.J.1016. 2010.01777.

XU Weizhi, SONG Fenglong, LIU Zhiyong,. On synchronization and evaluation method of chipped many-core processor[J]., 2010, 33(10): 1777-1787. doi: 10.3724/SP.J.1016.2010.01777.

冯 晓： 女，1987年生，博士生，研究方向为多核处理器、可重构芯片等.

戴紫彬： 男，1966年生，博士生导师，研究方向为专用芯片设计、可重构芯片、可重构SoC设计等.

李 伟： 男，1983年生，博士生，研究方向为大规模集成电路设计、多核处理器、信息安全等.

蔡路亭： 男，1989年生，硕士生，研究方向为信息安全、安全通信、SoC设计等.

Performance Model of Multicore Crypto Processor Based on Amdahl’s Law

FENG Xiao①DAI Zibin①LI Wei①②CAI Luting①

①(PLA Information Engineering University, Zhengzhou 450000, China)②(State Key Laboratory of Special Integrated Circuit and System, Fudan University, Shanghai 201203, China)

This paper builds a performance model of multicore processor, which applies to the crypto algorithms, and some advisable suggestions and academic supports are given for its design. By introducing parallelism degree, transformation overhead and synchronization time, performance model of multicore crypto processor is built based on the Amdahl’s law and its extension, and accordingly the design space of multicore crypto processors is searched. Simulation analysis shows that the key factors influencing the performance model of multicore crypto processor are the exploitable parallelism of crypto application, the proportion of parallel part and the communication times in the process of operation.

Crypto processor; Multicore processor; Amdahl’s law; Performance model; Communication/computing ratio

National Natural Science Foundation of China (61404175)

TP309.7；TN492

A

1009-5896(2016)04-0827-07

10.11999/JEIT150474

2015-04-27；改回日期：2015-12-25；网络出版：2016-02-18

李伟 try-1118@163.com

国家自然科学基金项目(61404175)