基于多重分形特征的通信调制方式识别研究

陈 红 蔡晓霞 徐 云 刘文涛



基于多重分形特征的通信调制方式识别研究

陈 红*①蔡晓霞①徐 云①刘文涛②

①(解放军电子工程学院 合肥 230037)②(解放军95915部队 天津 301612)

该文提出一种基于多重分形特征的数字通信信号调制方式识别新方法。对接收信号进行去噪预处理，基于2维数据阵列求取信号的广义维数和多重分形谱；详细讨论了权重因子对多重分形谱的影响，提取了13个多重分形特征参数；设计了基于多重分形特征的支持向量机分类器对不同信号进行调制方式识别。仿真结果表明，该算法在低信噪比情况下具有很好的识别性能。

调制方式识别；多重分形特征；广义维数；支持向量机

1 引言

随着通信技术的快速发展，复杂、多样的通信体制、调制方式使得通信信号调制方式识别越来越困难。要从本质上提高调制方式识别性能，特征选取至关重要。传统的基于信号的幅度、频率和相位瞬时特征[1]、时频特征[2]等通信信号调制方式识别方法受通信环境的影响很大，在低信噪比条件下的识别率会明显降低。基于高阶累积量特征[3,4]、循环谱特征[5,6]的识别方法在高斯噪声环境下识别性能较好，但是在短时大幅度脉冲背景噪声环境下识别性能明显下降甚至失效[7,8]，而且这类算法计算量较大，实时处理能力差。

信号分形特征作为反映信号“几何”特性的信息，是度量信号的复杂度和不规则度的重要手段，目前已应用于信号检测[9,10]、参数估计[11,12]和调制方式识别[7,13,14]等信号处理领域。但单分形维只是一个标度指数，只能对信号从整体或平均的角度进行定量描述，并未考虑信号在不同层次上的波动特征[15]。若要想全面完整地刻画通信信号的内部特性，就需要提取多重分形维数特征来描述目标信号。本文基于多重分形理论，提出了通过计算广义维数和多重分形谱，提取多重分形特征实现数字信号调制识别的新方法，仿真实验验证了该方法的有效性。

2 多重分形

多重分形又称分形测度，是定义在分形结构上的，由多个具有不同标度指数的奇异测度所组成的集合。把分形对象用尺度对其进行划分，得到单元，设是的线度大小，为的测度，且。可用标度指数来表示：

即

3 多重分形谱的计算

通信信号和噪声的广义维数和多重分形谱数值计算步骤如下：

(1)对接收到的1维信号时间序列进行去噪预处理，用固定长度的窗口去截取，依截取顺序按行排列，转换为一个2维数据阵列，根据2维数据阵列可以画出信号的纹理图案，图1给出了几种通信信号以及高斯白噪声的纹理图案，可以明显看出不同调制方式(2ASK, BPSK, QPSK, 2FSK, 16QAM等)、不同进制(BPSK, QPSK作为类内识别)信号之间的纹理差异，利用这一特性可以计算多重分形谱，获取信号在时间和空间上的相关分形特征，提取信号的多重分形特征参数用于信号调制方式识别。

(2)将2维数据阵列经中心化、归一化之后取绝对值得到幅度矩阵，记为矩阵的总质量。在此，我们选择截取信号窗口的大小为一个码元的采样长度，即窗口长度，得到的数据阵列为。

图1 不同信号的纹理图

图3是接收信号经过双树复小波变换预处理后，不同信噪比条件下BPSK信号的多重分形谱关系曲线。比较图2和图3：信号去噪处理前，随着信噪比的增大，曲线呈发散趋势，且奇异谱在不同信噪比条件下有很大的变化，如果不经过处理，则从中提取的特征不很稳定，受噪声影响较大，将影响识别结果。信号经过去噪处理之后，进一步削弱了噪声影响，多重分形谱更稳定一些，从而增加信号识别算法的噪声容限，提高识别正确率。

4 基于多重分形谱的特征参数提取

4.2 高斯白噪声的多重分形谱

4.3 通信信号分形特征参数提取

不同调制方式信号具有不同的分形特征，本文分别从质量指数、广义维数和多重分形谱中提取信号的多重分形特征参数用于信号调制方式识别。

图2 去噪前BPSK多重分形谱 图3 去噪后BPSK多重分形谱 图4 ,随的变化曲线

图5 不同方差下噪声多重分形曲线图

可以看出：多重分形谱函数是一个单峰曲线，进一步证明了通信信号存在多重分形特性，不同类型信号的多重分形谱曲线差异较大。因此，利用不同信号多重分形谱之间的差异提取如下特征参数：

5 基于多重分形特征参数的调制方式识别

5.1 分类器设计

不同调制方式信号之间特征的分布不是很均匀，特征的非线性比较明显，所以使用线性分类器或者基于距离的聚类分类算法效果不太好，在此我们使用支持向量机对其进行分类识别，它能较好地解决小样本、非线性、高维数和局部极小点等问题。

选择待识别的信号集为：2ASK, BPSK, QPSK, 8PSK, 16PSK, 2FSK, 4FSK, MSK和16QAM共9种数字调制信号。按照4.3节的方法，提取信号的13个分形特征参数，构成分类识别特征向量集，采用粒子群优化算法，对支持向量机参数进行寻优，设计支持向量机分类器训练和测试软件，进行信号方式识别。

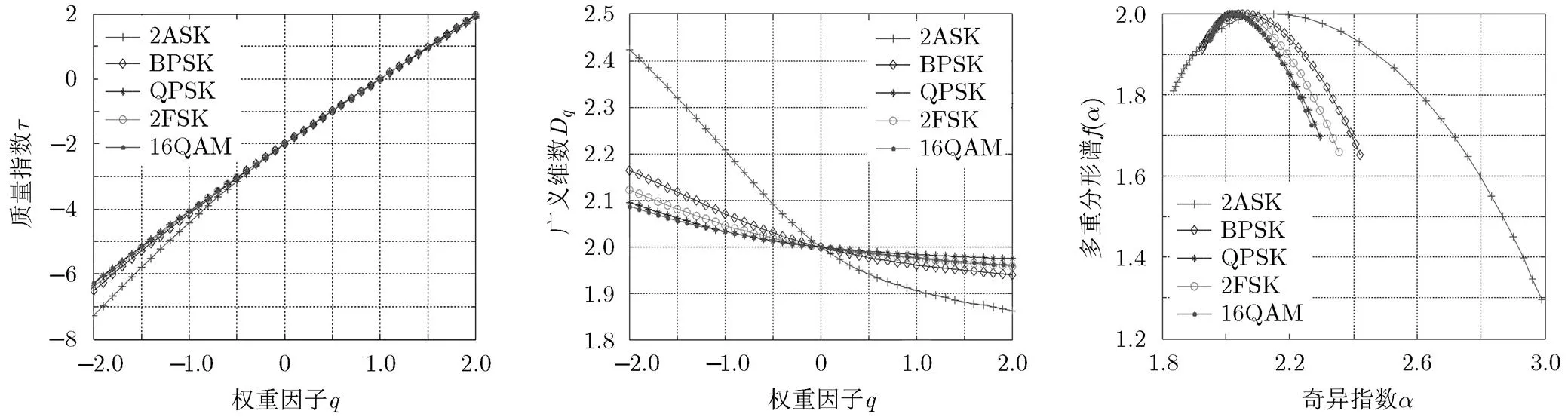
图6 质量指数与的关系曲线 图7 广义维数与的关系曲线 图8 多重分形谱与奇异指数的关系曲线

5.2 仿真分析

选择信噪比的变化范围为-3~20 dB，对每一类信号在信噪比大于0 dB时，每隔5 dB产生点的样本300个，在信噪比小于0 dB时，每隔1 dB产生点的样本300个，其中100个作为分类器的训练集，200个作为测试集，这样一来，每一类信号共有训练特征向量10400个，测试特征向量208000个。通过支持向量机学习训练之后，对不同通信信号进行调制方式分类识别，识别结果如表1所示。

可以看出，2ASK和BPSK的识别率最高，对QPSK, 8PSK及16PSK的识别效果在低信噪比情况下不太理想，因为在训练过程中混入了低信噪比的信号，噪声的影响减小了不同调制样式特征之间的距离，使得低信噪比下误判增多。本文基于多重分形特征算法的识别正确率明显高于文献[14]中基于单分形维数的识别率，能够实现低信噪比下数字信号的有效识别。

针对BPSK, QPSK, 8PSK, 16QAM，特征向量集及参数取值不变，重新设计支持向量机分类器，2000次仿真实验后统计得到信号正确识别率随着信噪比变化的曲线如图9所示。

结果表明：信噪比大于0 dB时，所有信号的正确识别率均可达到95%以上。随着信噪比下降，对BPSK, 16QAM的识别效果仍然较好，-6 dB时仍可达到90%以上的识别率，对QPSK, 8PSK的识别率下降，-3 dB时仍可达到70%左右的正确识别率，-6 dB时下降到50%以下。

将本文算法与文献[2]中基于小波变换的识别方法相比，比较结果如表2所示。

可见在信噪比较高的情况下，本文方法与文献[2]的识别效果相近，但信噪比较低时，本文算法的识别效果明显优于文献[2]，其原因在于多重分形对噪声不敏感。

5.3 数据验证

为了验证算法的实用性，采用一段QPSK的实测接收数据，中频为70 MHz，采样频率为40 MHz，信号带宽为5 MHz，脉冲成形波形采用滚降因子为0.22的升余弦脉冲，信噪比估算为10 dB。该信号的时频图如图10所示。

图9 不同信噪比情况下的正确识别率 图10 实测信号的时频图

表 1 基于多重分形特征的信号识别正确率(%)

进行1000次训练和识别的结果如表3所示，对实测QPSK信号的检测率为100%，识别成功率达到98%。

6 结束语

已调数字通信信号具有复杂的动力学特性，且这种复杂性在低信噪比下也能通过分形特征显现出

来。通过计算不同数字调制信号的多重分形谱，详细分析了多重分形谱的变化规律，提取了多个分形特征参数，设计支持向量机分类器进行调制方式识别。仿真实验证明了基于多重分形特征信号识别方法的有效性，且在低信噪比情况下也能取得很高的识别正确率，具有一定的实用价值。

[1] HEADLEY W C and DA SILVA C R. Asynchronous classification of digital amplitude-phase modulated signals in flat-fading channels[J]., 2011, 59(1): 7-12.

. 通信侦察信号处理关键技术研究[D]. [硕士论文], 电子科技大学, 2011.

LIAO Hongshu. A study of key technologies of signal processing for communication reconnaissance[D]. [Master dissertation], University of Electronic Science and Technology of China, 2011.

[3] SU W. Feature space analysis of modulation classification using very high-order statistics[J]., 2013, 17(9): 1688-1691.

[4] 张弛, 吴瑛, 周欣. 基于高阶累积量的数字调制信号识别[J]. 数据采集与处理, 2010, 25 (5): 575-579.

ZHANG Chi, WU Ying, and ZHOU Xin. Digital modulation recognition based on high-order cumulants[J].&, 2010, 25(5): 575-579.

[5] YU Ningyu, MA Hongguang, and SHI Rong. Modulation recognition of co-channel OQPSK and MSK based on cyclostationarity[C]. The 2nd International Conference on Information Management and Engineering, Chengdu, 2010: 284-287.

[6] 赵宇峰, 曹玉健, 纪勇, 等. 基于循环频率特征的单信道混合通信信号的调制识别[J]. 电子与信息学报, 2014, 36(5): 1202-1208. doi: 10.3724/SP.J.1146.2013.00454.

ZHAO Yufeng, CAO Yujian, JI Yong,. Modulation identification signals based single-channel mixed communication cyclic frequency features[J].&, 2014, 36(5): 1202-1208. doi: 10.3724/SP.J.1146.2013.00454.

. Alpha稳定分布噪声下通信信号调制识别研究[D]. [博士论文], 哈尔滨工程大学, 2012.

YANG Weichao. Modulation recognition for communication signals in the alpha-stable distribution noise[D]. [Ph.D. dissertation], Harbin Engineering University, 2012.

[8] 陈红, 蔡晓霞, 王晓翔. Alpha稳定分布噪声下的通信信号检测技术[J]. 中国人民解放军电子工程学院学报, 2015, 34(2): 20-24.

CHEN Hong, CAI Xiaoxia, and WANG Xiaoxiang. Detection technology for communication signals in the alpha-stable distribution noise[J]., 2015, 34(2): 20-24.

[9] 赵春晖, 马爽, 杨伟超. 基于分形盒维数的频谱感知技术研究[J]. 电子与信息学报, 2011, 33(2): 475-478. doi: 10.3724/SP.J.1146.2010.00400.

ZHAO Chunhui, MA Shuang, and YANG Weichao. Spectrum sensing in cognitive radios based on fractal box dimension[J].&, 2011, 33(2): 475-478. doi: 10.3724/SP.J.1146.2010.00400.

[10] 孙康, 金钢, 王超宇, 等. 扫描模式下海杂波的多分形布朗运动模型[J]. 电子与信息学报, 2015, 37(4): 982-988. doi: 10.11999/JEIT140730.

SUN Kang, JIN Gang, WANG Chaoyu,. Modeling sea clutter in radar scanning mode by multifractional Brownian motion[J].&, 2015, 37(4): 982-988. doi: 10.11999/JEIT140730.

[11] 李一兵, 李靖超, 林云. 基于分形盒维数的线性调频信号参数估计[J]. 系统工程与电子技术, 2012, 34(1): 24-27.

LI Yibing, LI Jingchao, and LIN Yun. Parameter estimation of LFM signals based on fractal box dimension[J]., 2012, 34(1): 24-27.

[12] 程曙晖, 王斌. 基于分形盒维数的跳频信号跳周期快速估计方法[J]. 信息工程大学学报, 2014, 15(2): 193-197.

CHENG Shuhui and WANG Bin. Fast estimation of hop duration of frequency-hopping signals based on fractal box dimension[J]., 2014, 15(2): 193-197.

[13] 党月芳, 徐启建, 张杰, 等. 高阶累积量和分形理论在信号调制识别中的应用研究[J]. 信号处理, 2013, 29(6): 761-765.

DANG Yuefang, XU Qijian, ZHANG Jie,. Research on modulation classification based on high-order cumulants and fractal theory[J]., 2013, 29(6): 761-765.

[14] 刘文涛, 陈红, 蔡晓霞, 等. 基于分形维数的数字信号调制方式识别[J]. 火力与指挥控制, 2014, 39(10): 1766-1768.

LIU Wentao, CHEN Hong, CAI Xiaoxia,. Digital modulation signal identification based on fractal dimension[J].&, 2014, 39(10): 1766-1768.

[15] CHAKRABORTY B, HARIS K, LATHA G,. Multifractal approach for seafloor characterization[J]., 2014, 11(1): 54-58.

[16] 唐智灵, 杨小牛, 李建东. 调制无线电信号的分形特征研究[J]. 物理学报, 2011, 60(5): 056401.

TANG Zhilin, YANG Xiaoniu, and LI Jiandong. Study on fractal features of modulated radio signal[J]., 2011, 60(5): 056401.

[17] 吴建飞, 袁学华. 基于小波多重分形的通信信号调制识别[J]. 航天电子对抗, 2014(3): 27-30.

WU Jianfei and YUAN Xuehua. Communication signal modulation recognition based on wavelet and multifractal[J]., 2014(3): 27-30.

[18] 郭鹏程, 孙龙刚, 李辉, 等. 多重分形及其改进算法研究[J]. 西安理工大学学报, 2014, 30(2): 139-144.

GUO Pengcheng, SUN Longgang, LI Hui,. Research on multifractal dimension and its improved algorithm[J].', 2014, 30(2): 139-144.

陈 红： 女，1965年生，教授，研究方向为通信信号处理和调制方式识别.

蔡晓霞： 女，1965年生，教授，研究方向为通信信号处理、隐匿通信与检测.

徐 云： 男，1972年生，讲师，研究方向为通信信号处理和信号参数估计.

Foundation Items: The National Natural Science Foundation of China (61571446), The Natural Science Foundation of Anhui Province (KY13C152)

Communication Modulation Recognition Based on Multi-fractal Dimension Characteristics

CHEN Hong①CAI Xiaoxia①XU Yun①LIU Wentao②

①(PLA Electronic Engineering Institute, Hefei 230037, China)②(Unit 95915 of PLA, Tianjin 301612, China)

A new modulation recognition algorithm of digital communication signals based on the multi-fractal dimension characteristics is proposed. Employing preprocessing the received signal, the generalized dimension and the multi-fractal spectrum can be calculated by 2D data array. The effect of multi-fractal spectrum due to the weighted factorsis discussed in detail, the 13 multi-fractal characteristic parameters are extracted. The Support Vector Machine (SVM) classifier based on the multi-fractal dimension characteristics is designed for recognition of different modulation signals. Simulation results show that the proposed method has a good recognition performance under low SNR.

Modulation recognition; Multi-fractal dimension characteristics; Generalized dimension; Support Vector Machine (SVM)

TN92

A

1009-5896(2016)04-0863-07

10.11999/JEIT150703

2015-06-08；改回日期：2015-12-11；网络出版：2016-02-29

陈红 hplanhf@126.com

国家自然科学基金(61571446)，安徽省自然科学基金(KY13C152)