一种低信噪比环境下的符号同步改进算法

张 玥，王 钢，赵海涛，郑黎明

一种低信噪比环境下的符号同步改进算法

张 玥1，王 钢1，赵海涛2，郑黎明1

（1.哈尔滨工业大学通信技术研究所，黑龙江哈尔滨150080；2.中国移动通信集团黑龙江有限公司，黑龙江哈尔滨150028）

针对OFDM符号同步基本算法在低信噪比条件下定时度量值低和干扰峰严重的缺点，提出了一种改进算法。该算法在基于训练序列符号同步的典型算法基础上，对训练序列的帧结构进行了改进，将共轭序列带入到帧结构中，同时改变了度量函数的计算方法。改进后的算法在低信噪比条件下有5 dB的性能提升，且具有计算量小、受信噪比影响小和实现简单等优点。仿真验证了改进算法在低信噪比环境下的有效性。

OFDM；低信噪比；符号同步；训练序列

引用格式：张 玥，王 钢，赵海涛，等.一种低信噪比环境下的符号同步改进算法［J］.无线电工程，2016，46（5）：33-36.

0 引言

正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）技术是属于多载波调制（Multicarrier Modulation，MCM）的一种，同时是一种无线环境下的高速传输技术［1］。目前OFDM在通信系统的快速发展主要得益于其关键技术：OFDM同步技术、降低峰均功率技术、空时编码技术和信道估计技术等，其中同步技术为现阶段常用的关键技术之一［2］。

符号同步技术是OFDM系统中同步技术的关键技术之一，国内外许多学者对OFDM系统的符号同步算法进行了研究。文献［3］中提出了一种基于窄带干扰的OFDM系统的同步算法，在复杂度增加的同时，在应用于电力线的基础上，提供了更尖锐的相关峰。文献［4］提出了 2种基于训练序列的OFDM符号同步算法，具有实现简单、计算量小及可迅速建立同步等优点。文献［5］提出了一种适用于DDO-OFDM系统的符号同步方法。文献［6-9］对原有算法函数进行了改进，提高了定时精度和系统性能。但这些算法都只是在接收信噪比较大的环境下能够获得良好的同步效果，而接收信噪比较差的环境下（5 dB以下）无法找到准确的符号同步位置，造成较大的同步误差。为了在信噪比较差的情况下尽可能地获得更好的符号同步性能，首先介绍了2种基于训练序列的经典同步算法，并在经典算法的基础上进行了发送端数据结构的改进，即对训练序列的帧结构进行了改进，同时改变了度量函数的计算方法。改进后的符号同步算法相比原算法，计算量更低，干扰相关峰更低，并且在低信噪比的情况下可以获得更好的同步性能。

1 系统模型描述

OFDM系统框图如图1所示。

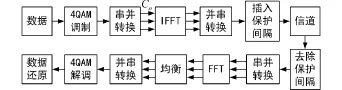
图1　OFDM系统框图

发送端，设待发送的OFDM符号数据在4QAM子载波调制后，串并转换后经过N点的快速傅里叶逆变换（IFFT）实现各子载波的基带调制，调制后OFDM系统中发送的基带符号的样值为：

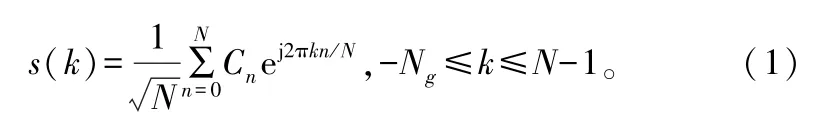
式中，经过4QAM调制后在第n个子载波上传输的数据为Cn；IFFT的点数（即子载波的个数）为N；循环前缀的宽度为Ng。

发送后的信号进入信道，离散时间信道的系统函数为：

式中，τi为路径i的时延；K为多径传输的信道总数。若接收端的抽样时钟的同步可以精确获得，信号接收端的接收信号为：

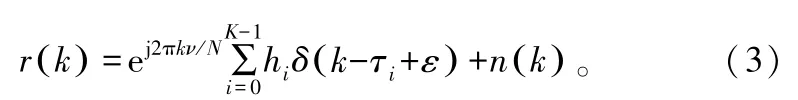
式中，ν为发射端和接收端的频率偏差；ε为传输符号的未知到达时间，其中ε为整数；n（k）为加性高斯白噪声。

在系统接收端对接收到的信号做符号定时、去前缀、频偏补偿和快速傅里叶变换（FFT）变换，最后根据判决准则恢复出发送信息［10］。

2 符号同步算法

符号同步（Symbol Timing Synchronization）位于OFDM系统的接收端，其作用是估计符号帧或帧头的起始时刻，以及在接收端信号经FFT变化前找到FFT窗口的精确位置。符号定时问题直接决定原始数据能否在接收端正确恢复出来，而符号同步算法可以很好地解决该问题［11］。

OFDM系统的符号同步方法可以分为非数据辅助类和数据辅助类两大类。非数据辅助类即在不使用辅助数据的条件下，仅仅利用循环前缀的自相关特性来达到同步性能，所以效率高，但易受噪声干扰，且精度较差。而数据辅助类符号同步方法，牺牲了一定的传输效率，在传输符号中加入特定的训练序列，可以在噪声环境下获取更高的同步性能。经典同步算法Schmidl&Cox同步算法和H.minn同步算法等属于数据辅助类符号同步方法。由于经典算法在低信噪比条件下的局限性，提出了一种改进的符号同步算法。

2.1 Schmidl&Cox同步算法

Schmidl&Cox同步算法［12］的训练序列结构如图2所示。

图2 Schmidl&Cox同步算法训练序列结构

图2中，Ng为循环前缀的长度，N为子载波个数。该训练序列由重复的2部分组成，每部分的序列长度为1/2的子载波个数，通过计算得到时间度量函数 M（d）。算法是通过寻找时间度量函数M（d）最大值的位置来完成定时估计的。

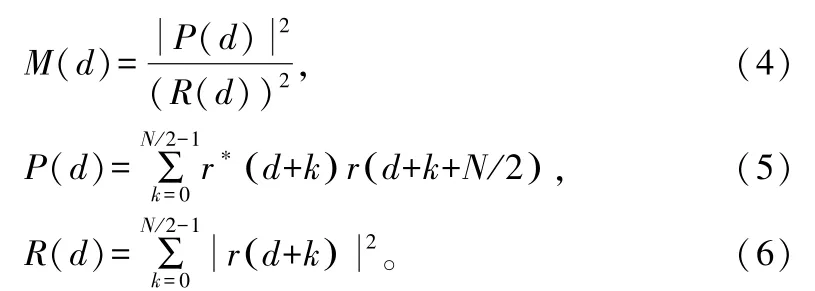
式中，r（k）为时域接收信号的数据；d为滑动窗口对应的第1个时间样值；P（d）为相关函数；R（d）为能量函数，作为P（d）归一化的量值。时间度量函数M（d）的最大值所对应的d值即为符号定时同步的估计位置。

由于存在循环前缀，Schmidl&Cox同步算法会存在一定长度的平顶区域，当没有噪声干扰时，平顶区域的理论长度应等于循环前缀的长度，平顶区域的存在会严重影响符号定时同步的准确性。且当信噪比较低时，度量函数的最大值过小，平顶干扰更加严重，也会造成符号同步定时不准确，定时误差增大。

2.2 H.minn同步算法

H.minn同步算法［13］是对Schmidl&Cox同步算法做出的改进算法。H.minn同步算法的训练序列结构如图3所示。

与Schmidl&Cox同步算法不同的是，H.minn同步算法将训练序列分为了4部分，长度均为子载波个数的1/4，训练序列的前半部分与Schmidl&Cox同步算法相同，后半部分是对前半部分的取反。

图3　H.minn同步算法训练序列结构

H.minn同步算法的时间度量函数如下：

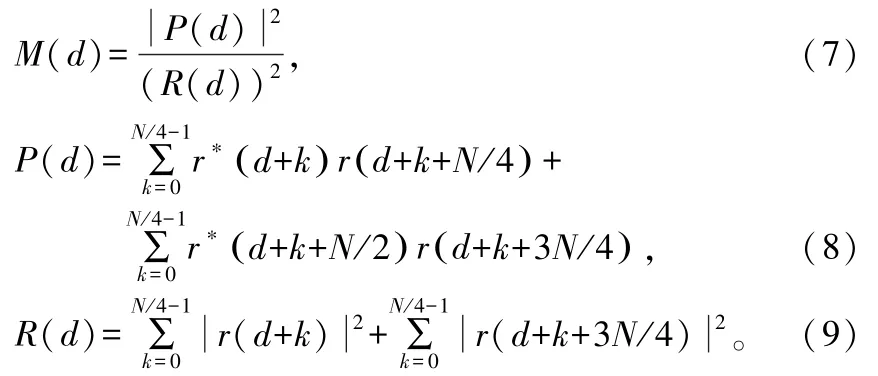
H.minn同步算法能够在符号同步定时位置处产生一个尖锐的峰值，有效地改进了Schmidl&Cox同步算法中的平顶区域。但H.minn同步算法也存在很大的缺陷，即在最大峰值的周围会产生几个干扰峰。当信噪比很小时会造成峰值误判，造成定时估计的不准确。

2.3 改进算法

由于Schmidl&Cox同步算法和H.minn同步算法在低信噪比条件下的缺陷，本文提出了一种低信噪比环境下OFDM系统的符号同步改进算法。改进的符号同步算法的训练序列结构如图4所示。

图4　改进算法训练序列结构

改进算法同H.minn同步算法一样将训练序列分为4部分，二者第1部分相同。改进算法的第2部分是对第1部分取反，后半部分对前半部分取共轭。改进同步算法的时间度量函数如下：

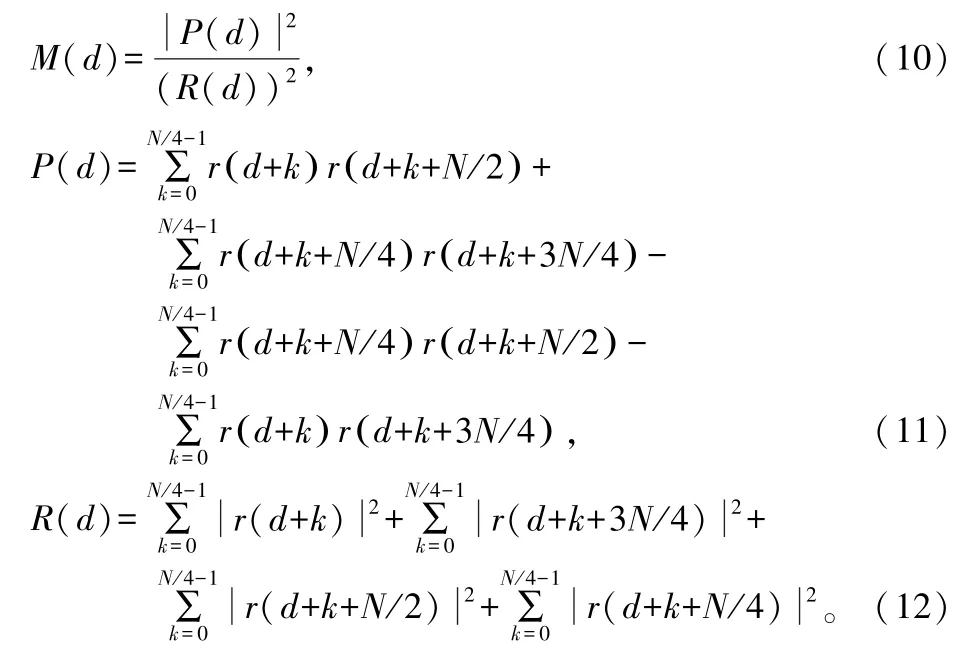
从改进算法的公式中可以看出，在乘法和加法的运算量没有变化的前提下，由于训练序列中存在共轭运算的序列，所以在计算时间度量函数时去除了共轭运算，一定程度上改进算法减小了算法的运算量。在消除了Schmidl&Cox同步算法定时测量平顶的同时，有效抑制了 H.minn同步算法副峰的产生。

3 性能仿真

3.1 仿真参数设置

仿真信道为高斯白噪声信道。用时间度量函数最大值来描述算法性能。仿真具体参数为：系统FFT点数为 256，传输数据循环前缀长度为32 bit，调制方式为4QAM调制，仿真次数为100，在SNR=-5 dB和SNR=25 dB之间进行仿真。

3.2 仿真结果

在无噪声条件下 Schmidl&Cox同步算法、H.minn同步算法及改进算法的时间度量曲线如图5所示。当信噪比SNR=0 dB时，3种算法的时间度量曲线如图6所示。当SNR分别为-5 dB、0 dB、5 dB和无穷大时改进算法的时间度量曲线如图7所示。在低信噪比条件下（SNR＜5 dB），各个算法的时间度量函数最大值随信噪比SNR变化曲线如图8所示。

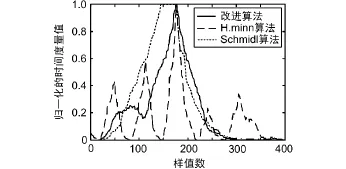
图5　无噪声条件下各个算法时间度量曲线

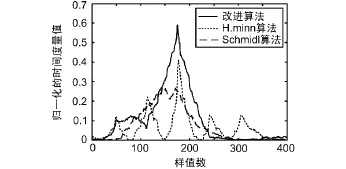
图6　SNR=0 dB各个算法时间度量曲线

由图5的仿真结果可以看出，在无噪声条件下Schmidl&Cox同步算法存在明显的峰值平台，而H.minn同步算法和本文改进算法函数峰值处曲线尖锐，且改进算法很大程度上避免了干扰峰值的产生，定时误差较小。由图6的仿真结果可以看出，此时Schmidl&Cox同步算法峰值不明显，定时误差很大。H.minn同步算法时间度量函数峰值不到0.4，相比较最大值1相差较大，且副峰干扰明显。改进算法时间度量函数峰值明显大于经典算法，且无副峰干扰。由图7的仿真结果可以看出，在SNR=-5 dB很低时，曲线依然具有尖锐的峰值，且没有副峰干扰，定时误差较小，定时位置准确。由图8仿真结果可以看出，当SNR＜5 dB时，改进算法峰值明显高于经典算法，相比经典算法受信噪比影响小，且随信噪比增加峰值趋近于1。在低信噪比条件下改进算法相比经典算法具有明显优势。

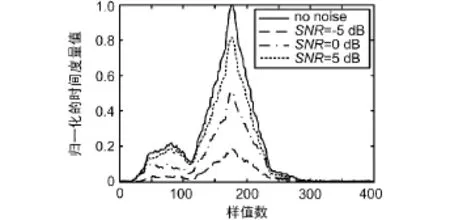
图7　改进算法时间度量曲线

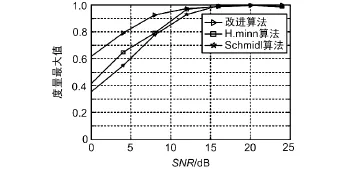
图8　峰值随SNR变化曲线

4 结束语

对传统的基于训练序列的符号同步算法进行了改进，将共轭序列引入到训练序列中，同时经过数学推导改变了度量函数的计算方法，并通过度量函数计算出的数值峰值能够寻找到同步位置。基于Matlab软件设计了验证算法有效性的实验，结果表明，改进后的算法在低信噪比条件下有5 dB的性能提升，当SNR＜5 dB时，改进算法的2个函数峰值明显高于经典算法，相比经典算法受信噪比影响小，所以在低信噪比条件下改进算法相比经典算法具有明显优势。本文研究的结果可以广泛应用于数据传输等方面。

［1］ DING C.An Improved Symbol Synchronization Method in OFDM Systems Based on Training Sequence［J］.Applied Mechanics and Materials，2015，713：1 273-1 276.

［2］ TANAKAYuki，INAMORIMamiko，SANADA Yukitoshi.Two Step Timing Synchronization Scheme for OFDM SignalinGeneralPurposeProcessorBased Software Defined Radio Receiver［J］.Wireless Personal Communications，2014，79（1）：363-374.

［3］ LIU Si-song，YANG Fang，SONG Jian，et al.OFDM Preamble Design for Synchronization Under Narrowband Interference［C］∥Power Line Communications and Its Applications（ISPLC），2013 17th IEEE International Symposium on.Johannesburg：IEEE Press，2013：252-257.

［4］ 费全荣.基于训练序列的OFDM符号同步算法研究［J］.舰船电子工程，2013（4）：123-125.

［5］ CHEN M，HE J，CAO Z，et al.Symbol Synchronization and Sampling Frequency Synchronization Techniques in RealtimeDDO-OFDMSystems［J］.OpticsCommunications，2014，326（5）：80-87.

［6］ 王 跃.基于训练序列的OFDM系统定时同步技术研究［D］.长春：吉林大学，2014：26-37.

［7］ 郑小真，孟艳花.基于训练序列的OFDM系统符号同步改进方法［J］.光通信研究，2013，39（1）：11-13.

［8］ 乔一新，赵晨霞，汤化新.基于交织训练序列的OFDM系统符号同步算法［J］.移动通信，2013（12）：82-86.

［9］ DING C.An Improved Symbol Synchronization Method in OFDM Systems Based on Training Sequence［J］.Applied Mechanics&Materials，2015，713（715）：1 273-1 276.

［10］祝晓霞，陈忠辉.OFDM系统符号同步研究及时间同步方法性能比较［J］.有线电视技术，2014（1）：53-56.

［11］BEEK Van de J J，BORJESSON P O，BOUCHERET M L.A Time and Frequency Synchronization Scheme for Multiuser OFDM［J］.SelectedAreasinCommunications，IEEE Journal on，1997，17（11）：1 900-1 914.

［12］SCHMIDL T M，COX D C.Robust Frequency and Timing Synchronization for OFDM［J］.Communications IEEE，1997，45（12）：1 613-1 621.

［13］MINN H，BHARGAVA V K，LETAIEF K B.A Robust Timing and Frequency Synchronization for OFDM Systems ［J］.Wireless Communications，IEEE Transactions on，2003，2（4）：822-839.

An Enhanced Symbol Synchronization Method for Low SNR OFDM Communications

ZHANG Yue1，WANG Gang1，ZHAO Hai-tao2，ZHENG Li-ming1
（1.Communication Research Center，Harbin Institute of Technology，Harbin Heilongjiang 150080，China；2.China Mobile Group Heilongjiang Co.，Ltd.，Harbin Heilongjiang 150028，China）

In view of the existence of high redundant peaks and of low timing metric when the classical methods are used in the condition of low SNR OFDM systems，a new symbol synchronization method with new training sequence and new timing metric calculation is proposed in this paper.The improved method has advantages of ease for implementation，smaller calculations and low influence by SNR difficultly.The effectiveness of the method will be verified by the simulation results.

OFDM；low SNR；symbol synchronization；training sequence

TN919.3+4

A

1003-3106（2016）05-0033-04

10.3969/j.issn.1003-3106.2016.05.09

2016-01-05

国家自然科学基金资助项目（61401120）。

张 玥 女，（1992—），硕士研究生。主要研究方向：移动通信和预编码技术。

王 钢 男，（1962—），教授，博士生导师。主要研究方向：无线通信和通信网络。