最小化类内距离和分类算法

王晓初 王士同 包 芳 蒋亦樟



最小化类内距离和分类算法

王晓初*①②王士同①包 芳②蒋亦樟①

①(江南大学数字媒体学院 无锡 214122)②(江阴 214405)

支持向量机分类算法引入惩罚因子来调节过拟合和线性不可分时无解的问题，优点是可以通过调节参数取得最优解，但带来的问题是允许一部分样本错分。错分的样本在分类间隔之间失去了约束，导致两类交界处样本杂乱分布，并且增加了训练的负担。为了解决上述问题，该文根据大间隔分类思想，基于类内紧密类间松散的原则，提出一种新的分类算法，称之为最小化类内距离和(Intraclass-Distance-Sum-Minimization, IDSM)分类算法。该算法根据最小化类内距离和准则构造训练模型，通过解析法求解得到最佳的映射法则，进而利用该最佳映射法则对样本进行投影变换以达到类内间隔小类间间隔大的效果。相应地，为解决高维样本分类问题，进一步提出了该文算法的核化版本。在大量UCI数据集和Yale大学人脸数据库上的实验结果表明了该文算法的优越性。

支持向量机；惩罚因子；大间隔分类思想；类内距离和；映射法则

1 引言

分类一直是人工智能和模式识别等领域研究的热点，分类算法广泛应用于数据挖掘、图像处理、视频跟踪与检测、智能收索、推荐系统、识别系统等领域，所以分类算法的发展与进步改变着人们的生产和生活方式。 目前常用的分类算法有决策树算法、贝叶斯分类器、K近邻算法、fisher判别分析法，神经网络算法和SVM等分类算法。决策树[1,2]是通过一定的规则对样本已知属性进行选择达到分类目的的算法。主要的决策树算法有ID3, C4.5等。ID3算法的目的在于减少树的深度，但不能处理具有连续值和具有缺失的数据属性。C4.5算法在ID3算法的基础上对于预测变量的缺值等方面作了较大的改进，使之适合于分类和回归问题。但决策树本身有容易过度拟合及忽略了数据集中属性之间的相关性等缺点。贝叶斯分类器[3,4]的分类原理是对属性决定类别可能性大小用训练样本进行判断，然后对新样本进行预测。贝叶斯分类算法假设数据属性之间是相对独立的，而现实中的问题并不总是这样。K近邻算法原理简单易于实现，但它假设样本每个属性的作用都是相同的，当数据集包含有许多不相关属性时，会误导分类过程。fisher判别分析法是找到一个映射法则，使得样本投影到该空间后能在保证方差最小的情况下，将不同的样本很好分开，但该算法仅仅用方差来衡量样本的离散程度，具有一定局限性。人工神经网络由众多的神经元可调的连接权值连接而成，具有大规模并行处理、分布式信息存储、良好的自组织自学习能力等特点。BP (Back Propagation)网络[11,12]是一种按误差逆向传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。人工神经网络算法和SVM (Support Vector Machine)都支持非线性分类，因此都有很高的精确率，但人工神经网络算法的可解释性不强，并且需要大量的参数。而SVM以其良好的抗噪声性能在小样本的分类上优秀的表现成为了目前最为常用的分类算法，但SVM最求间隔最大化，并没有太多关注类内样本间的关系，并且引入惩罚因子后增加了训练的难度。

关于SVM的改进大多在时间方面的优化：文献[17~19]提出SMO(Sequential Minimal Optimization), SVMlight和libSVM等算法，其中SVMlight和libSVM已经成为目前最常用的方法，这些算法将SVM时间复杂度由降低为。其他改进如文献[20]提出的拉格朗日支持向量机(LSVNM)等，最好的情况下可以达到。另外文献[21~23]将SVM推广到半监督领域。文献[24]提出了一种改进的支持向量机NN-SVM算法，它先对训练集进行修剪，根据每个样本与其最近邻类标的异同决定其取舍，然后再用SVM训练得到分类器，改善支持向量机的泛化能力。

上述方法都没有很好地解决引入惩罚因子后，错分的样本在分类间隔之间失去了约束，导致两类交界处样本杂乱分布的问题。本文提出的最小化类内距离和分类算法，利用样本通过映射法则投影到1维空间后可以在该1维空间重新分布的特性，对样本在该1维空间的分布进行训练。归一化投影后正负标签样本均值的相对间隔，且最小化投影后正负标签样本的类内距离和。训练后得到一个映射法则，样本通过该映射法则投影到1维空间后重新分布为线性可分的形式，同时该方法可引入核函数用于线性不可分的情况。该方法通过最小化类内距离和，使得样本投影到1维空间后同类样本的分布向各自均值集中，非同类样本产生间隔，使得分类更加容易。总地来说本研究的贡献主要有以下几个方面。(1)从距离和大间隔的角度提供了一种新的实现类内差异最小化，类间差异最大化思想下的分类算法。提出了最小化类内距离和准则，用于构造大间隔思想下的分类模型。可以选择不同的距离公式用于不同的要求。(2)适当避免了支持向量机分类算法引入惩罚因子来调节过拟合和线性不可分时无解的问题时允许一部分样本错分，错分的样本在分类间隔之间失去了约束，导致两类交界处样本杂乱分布的问题。同时优化了线性训练时参数选优带来的额外开销。

2 大间隔分类算法

近年来机器学习领域，间隔成为代表性的特征评估策略之一，已成为研究的热点。间隔概念首次由Vapnik在构建SVM模型时提出，SVM也成为运用了大间隔思想最具代表算法。图1为2维空间中对样本用SVM分类算法分类原理图，其中横、纵坐标分别表示样本的两个维度。

如图1所示，SVM的目的就是通过间隔最大化，找到最优超平面，其中且。当训练样本线性可分时，则存在超平面使得训练样本中的样本满足：

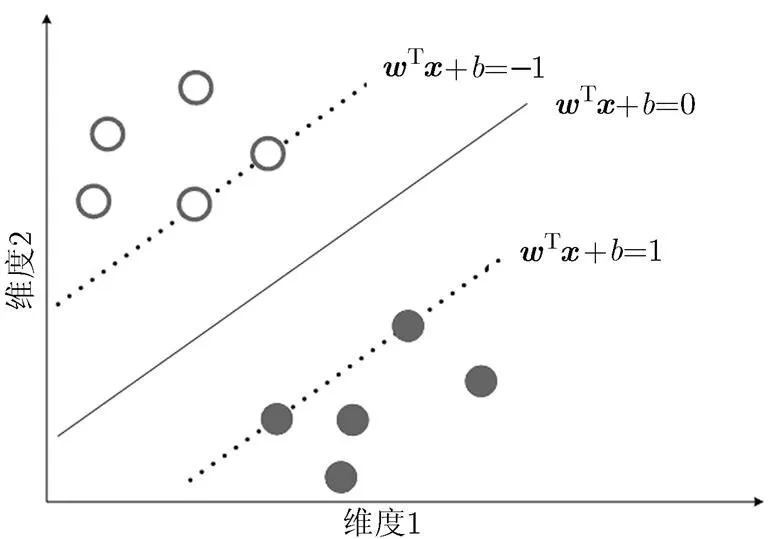
图1 SVM分类原理图

对于非线性问题，SVM通过引入核函数，其对应的对偶问题式(4)变为

最优决策超平面式(4)变为

支持向量机在分类过程中，利用结构化风险最小原理，求出最优决策超平面。并且引入惩罚因子来调节过拟合和线性不可分时无解的问题，这样做的好处是可以通过调节参数取得最优解，但同样带来的问题是训练时允许一部分样本错分，而允许错分的样本并不一定是噪声，错分的样本在分类间隔之间失去了约束，导致错分的样本在两类交界处样本杂乱分布；另外，引入参数后，增加了训练的成本。

3 最小化类内距离和分类算法

鉴于支持向量机的上述缺点，本文依据大间隔思想提出了最小化类内距离和(Intraclass- Distance-Sum-Minimization, IDSM)分类算法，该算法的原理是：将样本通过映射法则做投影变换，以最小化类内距离和为准则构造一个最大化类间间隔的训练模型，对该模型求解，寻找到最佳的映射法则。样本经过该最佳映射法则转化为线性可分问题。通过与之匹配的判别规则来判定未知样本的属性。由于本文采用最小化类内距离和准则，使得同类样本聚集，非同类样本相对远离，从而两类之间形成间隔。这样所有训练样本都向同类样本聚集。一定程度上解决了两类交界处样本杂乱分布的问题。另外，线性IDSM算法并不需要调节参数，相比支持向量机训练更加容易。图2展示了IDSM算法的构造原理。

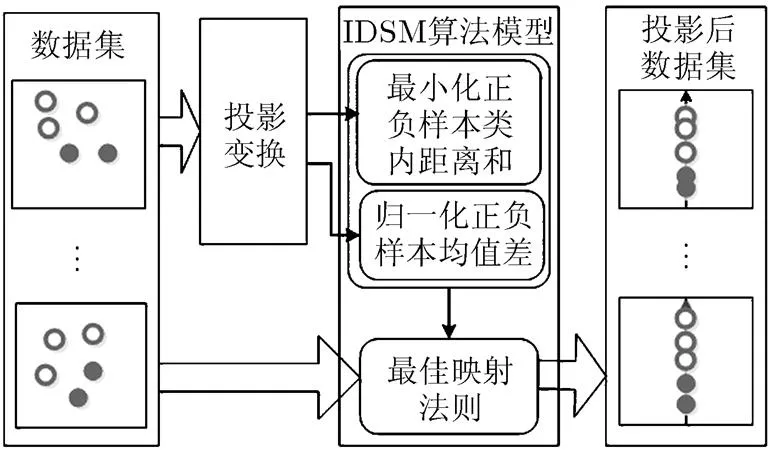
图2 IDSM算法构造原理

为了更加清晰地说明两者的区别，本文在两类服从高斯分布的2维数据(如图3(a))上进行模拟实验， 图3(b)是惩罚因子取0.001时的SVM的分类结果的3维图，可清晰看到两类交界处附近点的分布很杂乱。图3(c)是欧氏距离和用于本文算法所得的结果，可以看到两类样本在投影后的空间上均值相对间隔为1，并且两类样本聚集在同类均值附近，类内更加紧凑，类间相对形成间隔。

3.1 IDSM算法框架的提出

样本间的距离和反映了样本在类内的聚集程度。距离和越小，样本越集中。假设两样本间的距离用表示。训练样本集包含个特征为的样本。由训练集的前个样本组成。

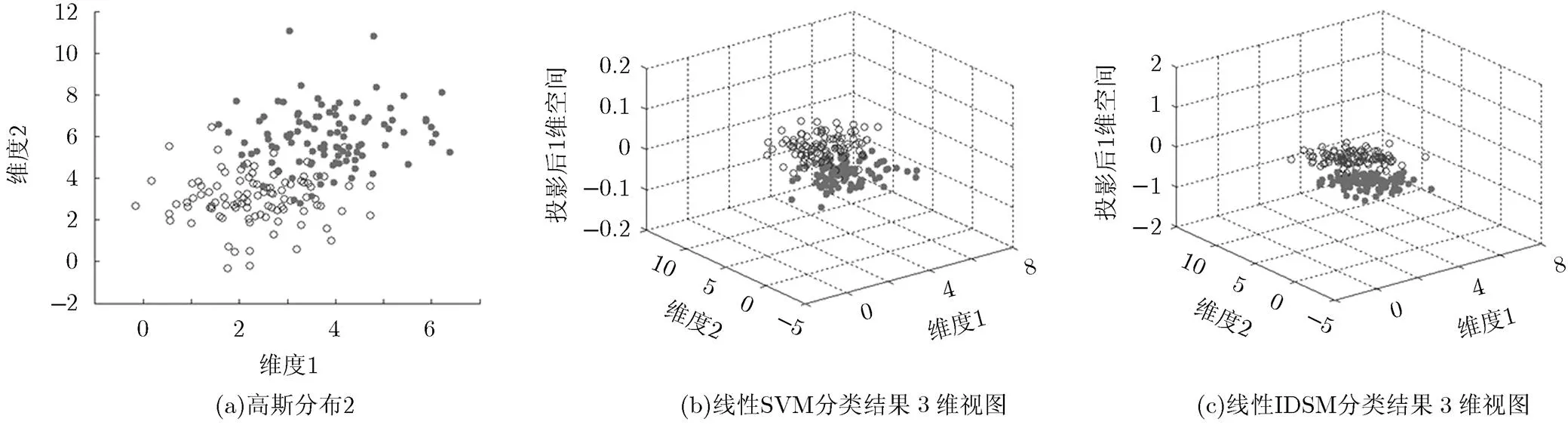
图3 SVM与IDSM算法区别示意图

正样本和负样本的均值表达式为

归一化正负样本均值差且最小化类内距离和，得到IDSM算法训练模型：

得到的模型可以用递归最小二乘算法进行求解，进而得到最佳映射法则。对于测试样本，通过最优映射法则投影变换得到：。由于IDSM算法训练模型使得投影后的样本类内距离和达到最小，同类样本向各自均值聚集，从而类间产生间隔。那么，通过最优映射法则变换得到的测试样本便具有靠近同类样本均值，远离非同类样本的特性。因此，可以通过比较经过最佳映射法则投影变换后测试样本与正负训练样本均值之间的距离来判断样本的属性。假设测试样本到正训练样本均值的距离，到负训练样本均值的距离。IDSM算法具体判别规则：

上面介绍了IDSM算法的训练模型和判别方法，IDSM算法提供了一个框架，可以在不同的需求下选择不同的距离公式。本文选用欧氏距离公式来推理验证IDSM算法的有效性。欧氏距离公式下的IDSM算法简称为EIDSM。3.2节是对EIDSM算法的推导。

3.2 EIDSM算法

欧氏距离作为IDSM算法中距离和的衡量标准，投影变换后两样本间的距离为

那么，欧氏距离和表达式：

那么欧氏距离和式(15)，式(16)衡量的最小化类内距离和分类算法(EIDSM算法)，去掉常数2，不影响结果，得目标函数：

3.3 非线性EIDSM算法

设

此时正样本欧氏距离和的非线性表达式可化简为矩阵形式：

同理，负样本欧氏距离和的非线性表达式可化简为矩阵形式：

那么非线性欧氏距离和式(24)，式(25)衡量的最小化类内距离和分类算法(非线性EIDSM)，去掉常数2，不影响结果，可以写成如式(26)目标函数：

判别方法见3.1节式(12)。

4 目标函数求解算法

目标函数式(17)，式(26)是非线性有约束优化问题，并且是凸优化问题。有多种方法可以选择，比如拟牛顿法，Rosen梯度投影法等，线性和非线性目标函数可以化简到相同的形式，我们只解析线性目标函数算法过程。这里我们用解析法对该优化问题进行求解，算法步骤如下：

步骤 2 目标函数式(17)可写为

步骤 7 重复步骤5，步骤6直到收敛或满足停止条件；

步骤 9 根据式(12)对新样本进行归类。

分析最小二乘的递归求解过程，本文算法在线性和非线性的时间复杂度分别为和，为最小二乘算法收敛时循环的次数。

5 实验与分析

设计了两组试验来验证本文方法的有效性。第1组用UCI公共有效数据集中的10个数据集进行随机抽取75%的样本用于训练，剩余的25%用于测试，记录正确率和每次运行所用时间(s)。表1列出了10个UCI数据集的信息。第2组用Yale大学人脸数据库，在小样本下，不断增加训练样本个数，记录正确率和每次运行所用时间(s)。这样设计可验证其在小样本上的表现。鉴于IDSM算法和fisher用于分类的算法[32]都具有使类内样本聚集的特点，相同之处在于他们都利用了最小化类内差异的思想，区别在于IDSM算法是用距离来度量类内和类间的差异，而fisher用于分类算法是用方差来度量类内差异；其次IDSM算法由于引入了，对不平衡数据适应性相对较好。所以用SVM和fisher作为EIDSM算法的对比试验。表2包含了对实验平台和部分算法英文缩写的说明。

5.1 UCI数据集

表1 UCI数据集信息

数据集

breast

cleve

German

haberman

heart

ionosphere

liver

pima

sonar

WBC

正样本个数

81

160

300

225

150

126

145

268

111

444

负样本个数

196

136

700

81

120

225

200

500

97

239

属性个数

9

13

24

3

13

34

6

8

60

9

表2 实验说明

实验平台

CPU: Intel(R)Core(TM)2Duo 3.00 GHz

RAM: 4.00 GB

系统：64位Win8.1操作系统

工具：32位MatlabR2012a

实验中缩写算法的全称

LSVM：线性支持向量机

KSVM：非线性支持向量机

LFISHER: fisher线性判别分类算法

KFISHER：核fisher判别分类算法

LEIDSM：线性欧氏距离和衡量的最小化类内距离和分类算法

KEIDSM：非线性欧氏距离和衡量的最小化类内距离和分类算法

表3 UCI数据集的正确率测试结果(%)

UCI

LSVM

KSVM

LFISHER

KFISHER

LEIDSM

KEIDSM

breast

75.36±3.92

75.71±4.74

66.81±3.58

72.17±2.38

72.17±5.19

74.88±2.11

cleve

51.30±4.38

68.15±5.62

81.43±2.31

81.84±3.50

82.59±3.52

83.01±2.33

German

32.16±1.71

73.32±1.88

71.60±3.35

71.68±2.20

73.84±2.01

69.20±3.86

haberman

71.84±3.34

77.37±4.96

72.76±3.40

76.58±2.35

75.63±0.72

79.39±2.47

heart

51.34±3.89

68.36±2.45

83.13±4.39

80.30±4.34

87.16±3.27

80.63±3.11

ionosphere

88.41±8.22

91.82±3.25

87.16±2.99

87.27±3.15

90.91±2.41

89.39±5.37

liver

52.56±9.60

64.19±3.03

61.63±4.87

62.09±2.11

64.88±7.04

67.83±2.69

pima

46.06±17.68

69.06±4.37

73.83±3.09

69.08±3.13

77.92±2.46

76.83±2.27

sonar

79.52±4.17

86.92±2.85

73.00±6.14

73.63±8.64

75.00±3.85

80.13±4.84

WBC

96.37±1.12

97.89±0.89

96.19±0.88

97.54±0.64

96.61±0.96

97.96±0.89

均值

64.49±5.80

77.28±3.40

76.75±3.50

77.22±3.24

79.67±3.14

79.93±2.99

表4 UCI数据集的时间测试结果(s)

UCI

LSVM

KSVM

LFISHER

KFISHER

LEIDSM

KEIDSM

breast

0.1719±0.0082

0.0780±0.0061

0.0035±0.0004

0.1156±0.0301

0.0040±0.0004

0.1780±0.0060

cleve

0.4265±0.2948

0.0961±0.0039

0.0031±0.0003

0.0906±0.0007

0.0043±0.0003

0.0746±0.0028

German

3.7270±0.5067

0.6778±0.0139

0.0094±0.0037

1.3044±0.2950

0.0181±0.0012

2.6074±0.3863

haberman

0.2881±0.2186

0.0762±0.0110

0.0041±0.0035

0.1088±0.0381

0.0035±0.0005

0.2166±0.0130

heart

0.4100±0.2112

0.0839±0.0048

0.0047±0.0005

0.0781±0.0053

0.0043±0.0005

0.0682±0.0032

ionosphere

0.4992±0.2488

0.1208±0.0049

0.0063±0.0004

0.1469±0.0075

0.0081±0.0004

0.3057±0.0075

liver

0.2979±0.1338

0.0764±0.0057

0.0054±0.0011

0.1031±0.0013

0.0044±0.0009

0.1621±0.0080

pima

1.0151±0.3822

0.2824±0.0079

0.0070±0.0005

0.3719±0.0104

0.0096±0.0007

0.5191±0.0202

sonar

0.6587±0.1144

0.0679±0.0046

0.0062±0.0002

0.0500±0.0020

0.0100±0.0004

0.0654±0.0045

WBC

0.1167±0.0442

0.1290±0.0029

0.0031±0.0017

0.5125±0.0036

0.0089±0.0009

1.4975±0.3204

均值

0.7611±0.2163

0.1689±0.0066

0.0043±0.0012

0.2882±0.039

0.0075±0.0006

0.5695±0.0752

根据表3所示，通过比较本文LEIDSM算法与其他对比算法在各UCI数据集上的实验结果可知：

(1)LEIDSM和KEIDSM算法在大部分数据集上取得了比LSVM和KSVM更高的正确率。说明本文算法的通过类内距离和最小化准则构造的大间隔分类模型在一定程度上优于SVM结构风险化最小和引入惩罚因子构造的标准SVM大间隔分类模型。

(2)LEIDSM和KEIDSM算法在大部分数据集上取得了比LFISHER和KFISHER更高的正确率。分析数据知，对于正负样本个数差别不大的数据集，如cleve, liver, sonar等上的表现，fisher用于分类的算法与本文算法正确率差距相对较小，而在正负样本个数差别很大的数据集，如breast等上的表现，fisher算法与本文算法正确率差距相对较大。这是由于本文算法在提出时便考虑到样本不平衡时算法的适应性问题，加入了参数，一定程度上解决了数据样本不平衡带来的不适性。而fisher算法认为两类均衡，在不平衡数据集上表现相对较差。

根据表4所示，线性方面，LFISHER平均用时最短，LSVM用时最长，LEIDSM介于他们之间。非线性方面，KSVM用时最短。由于本文采用递归最小二乘法对算法进行求解，在线性时时间复杂度为，非线性时时间复杂度为。而fisher算法线性和非线性时间复杂度分别为和。由于SVM用经典的改进算法SMO作对比，SMO在线性和非线性平均时间复杂度为。分析实验中UCI数据集知，几乎所有数据集的特征个数远小于训练样本数，因此在线性时有，所以fisher算法平均用时最短。而非线性时，在训练样本个数相同的情况下，有，所以KSVM用时最短。

5.2 Yale大学人脸数据库

Yale大学人脸数据库由Yale大学计算视觉与扼制中心创立，包括15位志愿者的165张图片，每人11张照片，主要包括光照条件和表情等的变化，每幅图片重新采样为10×10的大小。实验参数的设置与5.1节相同，实验中采取两两配对的方法，共有105种配对方式，在每个训练样本级别都取这105种准确率结果的平均值。每个图像分别用2, 3, 4, 5, 6, 7, 8, 9, 10个进行训练，剩下的样本作为测试样本。表5记录了5次独立重复实验的正确率均值，表6记录了平均每次运行所用的时间均值。

依据表5所示，样本变化时，随着训练样本的增多，各种算法下分类的正确率几乎都有提升。

(1)比较各算法线性情况在样本变时的表现：LEIDSM大部分情况下比LSVM和LFISHER正确率高。这是由于人脸本身是非线性的，SVM引入惩罚因子来解决非线性无解的情况，允许部分样本错分，错分后的样本在两类交界处杂乱分布。而本文算法，使得投影变换后的样本向各自均值聚集，并且本文算法训练和判别都用距离最小准则，训练和判别更加匹配，所以更有利于分类。

(2)比较各算法非线性情况在样本变化时的表现：在样本个数较少时，KSVM比KEIDSM和KFISHER表现要好，而当样本个数增大到一定程度时，KEIDSM表现更好。这是因为SVM只需关键的支持向量，所以对小样本有很强的学习能力。而样本增加时，本文算法的类内距离和利用了更多的样本信息，所以取得了更好的结果。另外，由于实验105个配对分类，每次实验对不同的人脸图像分类选用的是同一个参数，若是算法对参数较为敏感，实验结果会偏差。

表5 Yale人脸数据库实验准确率测试结果(%)

Yale

LSVM

KSVM

LFISHER

KFISHER

LEIDSM

KEIDSM

2

81.48±17.41

88.35±13.34

88.41±24.52

84.11±14.21

91.80±8.89

86.98±8.95

3

85.60±14.17

86.42±15.70

93.21±9.33

81.79±15.19

92.62±9.45

87.68±9.96

4

88.44±10.02

89.09±10.3

91.16±10.46

82.04±15.09

92.04±10.21

88.78±8.63

5

91.43±7.88

91.75±7.96

94.05±7.55

80.57±16.74

94.29±8.36

86.67±10.80

6

89.43±12.62

92.00±9.24

93.81±8.01

85.43±17.37

92.48±10.72

90.67±8.69

7

91.19±10.67

91.43±1.30

94.16±5.23

86.50±18.70

91.79±11.73

91.67±9.44

8

88.73±13.30

89.05±13.24

95.24±8.24

89.31±18.12

95.87±7.59

93.02±9.18

9

93.57±11.51

94.76±6.67

94.76±10.79

90.71±17.63

96.67±8.54

96.90±8.66

10

93.81±16.55

94.47±9.76

92.38±11.03

86.67±16.51

96.67±12.53

97.14±10.06

表6 Yale人脸数据库实验时间测试结果(s)

Yale

LSVM

KSVM

LFISHER

KFISHER

LEIDSM

KEIDSM

2

0.0059±0.0008

0.0049±0.0003

0.0060±0.0004

0.0025±0.0003

0.1378±0.2362

0.0303±0.0554

3

0.0069±0.0009

0.0053±0.0009

0.0071±0.0003

0.0058±0.0007

0.0085±0.0026

0.0069±0.0005

4

0.0070±0.0014

0.0055±0.0009

0.0071±0.0017

0.0060±0.0007

0.0171±0.0083

0.0076±0.0003

5

0.0073±0.0019

0.0066±0.0016

0.0079±0.0006

0.0042±0.0002

0.0077±0.0003

0.0084±0.0005

6

±0.0015

0.0071±0.0009

0.0077±0.0006

0.0075±0.0013

0.0073±0.0005

0.0092±0.0010

7

0.0093±0.0017

0.0088±0.0016

0.0109±0.0012

0.0057±0.0005

0.0110±0.0004

0.0095±0.0006

8

0.0105±0.0025

0.0090±0.0014

0.0116±0.0009

0.0126±0.0111

0.0145±0.0011

0.0103±0.0007

9

0.0125±0.0039

0.0098±0.0009

0.0058±0.0018

0.0135±0.0056

0.0078±0.0008

0.0113±0.0009

10

0.0104±0.0030

0.0101±0.0011

0.0094±0.0002

0.0138±0.0019

0.0082±0.0009

0.0116±0.0004

依据表6所示，样本增加时各算法用时都变长。大部分情况下LSVM和KSVM用时更短，这是由于图片本身维度为100维，所以有，此时LEIDSM, LFISHER失去了线性方面时间复杂度的优势。

6 结束语

本文依据大间隔思想，提出了最小化类内距离和分类算法。并且在欧式距离标准下对本文算法进行推理实验，通过与SVM和fisher判别分类算法的比较，证明了该分类算法的有效性。另外，本文只在欧氏距离下验证了算法的有效性，欧氏距离要求数据样本在模式空间中呈球状分布，接下来的工作可以针对不同的数据选择不同的距离公式来构建距离矩阵拓展本文算法。该分类算法时间复杂度方面还有待改进，且该分类算法是一种二分类算法，对于多类问题，需要设计多分类器。

[1] QUINLAN J R. Induction of decision trees[J].,1986, 1(1): 81-106.

[2] QUINLAN J R. Improved use of continuous attributes in C4.5[J]., 1996, 4(1): 77-90.

[3] PENG F, SCHUURMANS D, and WANG S. Augmenting naive Bayes classifiers with statistical language models[J]., 2004, 7(3/4): 317-345.

[4] CHENG J and GREINER R. Comparing Bayesian network classifiers[C]. Proceedings of the Fifteenth Conference on Uncertainty in Artificial Intelligence, San Francisco, USA, 1999: 101-108.

[5] COVER T and HART P. Nearest neighbor pattern classification [J].,1967, 13(1): 21-27.

[6] BIJALWAN V, KUMAR V, KUMARI P,. KNN based machine learning approach for text and document mining[J].2014, 7(1): 61-70.

[7] 黄剑华, 丁建睿, 刘家锋, 等. 基于局部加权的Citation-kNN算法[J]. 电子与信息学报, 2013, 35(3): 627-632.

HUANG Jianhua, DING Jianrui, LIU Jiafeng,. Citation- kNN algorithm based on locally-weighting[J].&, 2013, 35(3): 627-632.

[8] WELLING M. Fisher linear discriminant analysis[J]., 2008, 16(94): 237-280.

[9] FUIN N, PEDEMONTE S, ARRIDGE S,. Efficient determination of the uncertainty for the optimization of SPECT system design: a subsampled fisher information matrix[J]., 2014, 33(3): 618-635.

[10] DUFRENOIS F. A one-class kernel fisher criterion for outlier detection[J].&, 2014, 26(5): 982-994.

[11] VAN Ooyen A and NIENHUIS B. Improving the convergence of the back-propagation algorithm[J]., 1992, 5(3): 465-471.

[12] 潘舟浩, 李道京, 刘波, 等. 基于BP算法和时变基线的机载InSAR数据处理方法研究[J]. 电子与信息学报, 2014, 36(7): 1585-1591.

PAN Zhouhao, LI Daojing, LIU Bo,. Processing of the airborne InSAR data based on the BP algorithm and the time-varying baseline[J]&, 2014, 36(7): 1585-1591.

[13] SUYKENS J A K and VANDEWALLE J. Least squares support vector machine classifiers[J]., 1999, 9(3): 293-300.

[14] 胡文军, 王士同, 王娟, 等. 非线性分类的分割超平面快速集成方法[J]. 电子与信息学报, 2012, 34(3): 535-542.

HU Wenjun, WANG Shitong, WANG Juan,. Fast ensemble of separating hyperplanes for nonlinear classification[J].&, 2012, 34(3): 535-542.

[15] GAO X, LU T, LIU P,. A soil moisture classification model based on SVM used in agricultural WSN[C]. 2014 IEEE 7th Joint International, Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, 2014: 432-436.

[16] RIES C X, RICHTER F, ROMBERG S,. Automatic object annotation from weakly labeled data with latent structured SVM[C]. 2014 12th IEEE International Workshop on Content-based Multimedia Indexing (CBMI), Klagenfurt, Austria, 2014: 1-4.

[17] PLATT J. Fast training of support vector machines using sequential minimal optimization[J].:, 1999(3): 185-208.

[18] JOACHIMS T. Making large scale SVM learning practical[R]. Universität Dortmund, 1999.

[19] CHANG C C and LIN C J. LIBSVM: A library for support vector machines[J].&, 2011, 2(3): 389-396.

[20] MANGASARIAN O L and MUSICANT D R. Lagrangian support vector machines[J]., 2001, 1(3): 161-177.

[21] SEOK K. Semi-supervised regression based on support vector machine[J].&, 2014, 25(2): 447-454.

[22] LENG Y, XU X, and QI G. Combining active learning and semi-supervised learning to construct SVM classifier[J].-, 2013, 44(1): 121-131.

[23] CHEN W J, SHAO Y H, XU D K,. Manifold proximal support vector machine for semi-supervised classification[J]., 2014, 40(4): 623-638.

[24] 李红莲, 王春花, 袁保宗. 一种改进的支持向量机NN- SVM[J]. 计算机学报, 2003, 26(8): 1015-1020.

LI Honglian, WANG Chunhua, and YUAN Baozong. An improved SVM: NN-SVM[J]., 2003, 26(8): 1015-1020.

[25] 陈宝林. 最优化理论与算法[M]. 北京: 清华大学出版社, 2005: 281-322.

CHEN Baolin. Optimization Theory and Algorithm[M]. Beijing, Tsinghua University Press, 2005: 281-322.

[26] YOSHIYAMA K and SAKURAI A. Laplacian minimax probability machine[J]., 2014, 37: 192-200.

[27] MIGLIORATI G. Adaptive polynomial approximation by means of random discrete least squares[J].&, 2013, 103: 547-554.

[28] HUANG K, YANG H, KING I,. The minimum error minimax probability machine[J]., 2004(5): 1253-1286.

[29] PLAN Y and VERSHYNIN R. Robust 1-bit compressed sensing and sparse logistic regression: A convex programming approach[J].,2013, 59(1): 482-494.

[30] ALIZADEN F. Interior point methods in semidefinite programming with applications to combinatorial optimization[J]., 1995, 5(1): 13-51.

[31] BOYD S and VANDENBERGHE L. Convex Optimi- zation[M]. Cambridge University Press, 2009: 127- 214.

[32] 边肇祺, 张学工. 模式识别[M]. 北京: 清华大学出版社, 2001: 83-90.

BIAN Zhaoqi and ZHANG Xuegong. Pattern Recognition[M]. Beijing, Tsinghua University Press, 2001: 83-90.

王晓初： 男，1987年生，硕博连读生，研究方向为模式识别、数字图像处理.

王士同： 男，1964年生，教授，研究方向为人工智能、模式识别、生物信息.

包 芳： 女，1970年生，教授，研究方向为人工智能、模式识别.

蒋亦樟： 男，1988年生，博士，研究方向为模式识别、智能计算.

Foundation Items: The National Natural Science Foundation of China (61170122, 61272210)

Intraclass-Distance-Sum-Minimization Based Classification Algorithm

WANG Xiaochu①②WANG Shitong①BAO Fang②JIANG Yizhang①

①(School of Digital Media, Jiangnan University, Wuxi 214122, China)②(Information Fusion Software Engineering Research and Development Center of Jiangsu Province, Jiangyin 214405, China)

Classification algorithm of Support Vector Machine (SVM) is introduced the penalty factor to adjust the overfit and nonlinear problem. The method is beneficial for seeking the optimal solution by allowing a part of samples error classified. But it also causes a problem that error classified samples distribute disorderedly and increase the burden of training. In order to solve the above problems, according to large margin classification thought, based on principles that the intraclass samples must be closer and the interclass samples must be looser, this research proposes a new classification algorithm called Intraclass-Distance-Sum-Minimization (IDSM) based classification algorithm. This algorithm constructs a training model by using principle of minimizing the sum of the intraclass distance and finds the optimal projection rule by analytical method. And then the optimal projection rule is used to samples’ projection transformation to achieve the effect that intraclass intervals are small and the interclass intervals are large. Accordingly, this research offers a kernel version of the algorithm to solve high-dimensional classification problems. Experiment results on a large number of UCI datasets and the Yale face database indicate the superiority of the proposed algorithm.

Support Vector Machine (SVM); Penalty factor; Large margin classification thought; Sum of intraclass distance; Projection rule

TP391.41

A

1009-5896(2016)03-0532-09

10.11999/JEIT150633

2015-05-04；改回日期：2016-01-05；网络出版：2015-11-19

王晓初 icnice@yeah.net

国家自然科学基金(61170122, 61272210)