Turbo均衡中的符号方差反馈均衡器

武岩波 房小芳 朱 敏



Turbo均衡中的符号方差反馈均衡器

武岩波*①②房小芳②③朱 敏①②

①(中国科学院声学研究所声场声信息国家重点实验室 北京 100190)②(中国科学院声学研究所海洋声学技术中心 北京 100190)③(中国科学院大学 北京 100190)

为了降低Turbo均衡中均衡器的复杂度，该文提出了符号方差反馈均衡算法(SVFE)。该算法是对精确的线性最小均方误差估计值(LMMSE)进行Taylor展开得到的。在该算法中，先利用时不变均衡器得到初步符号估计值，再根据先验符号方差对估计值加权，最后进行时不变滤波得到更佳的符号估计值。由于用到了时变的先验符号方差信息，其性能更接近精确的LMMSE均衡器。将所提算法用于Proakis C信道下的Turbo均衡处理，和时不变均衡算法进行仿真对比，所提算法将信噪比损失从0.83 dB降到了0.17 dB，并且仍可通过快速傅里叶变换降低为对数复杂度。

Turbo均衡；软输入软输出均衡；最小均方误差线性均衡器

1 引言

信道的多径效应造成码间干扰，导致通信性能的恶化；信道编码通过人为地增加冗余可显著提高通信的质量。对具有码间干扰的编码符号进行最佳检测，应根据接收到序列样本，在编码符号序列空间中找到最大似然值，进而得到原始信息比特序列的最佳估计值。直接的最佳联合检测算法需要遍历所有的信息比特序列，因而难以实时地完成计算工作量。利用Turbo迭代原理，人们提出Turbo均衡算法，将信息比特序列的软信息在软输入软输出(Soft-Input Soft-Output, SISO)均衡器和SISO译码器之间进行多次迭代，降低了计算复杂度，其性能接近最佳联合检测算法，且明显优于均衡和译码的单步处理方式。由于SISO译码器在Turbo码中的研究较为成熟，且和信道多径没有直接的关联，不同Turbo均衡算法间的主要区别在SISO均衡器的性能和计算复杂度。SISO均衡按照结构划分，可分为基于格型结构的SISO均衡器和基于滤波器结构的SISO均衡器。

最早提出Turbo均衡算法时采用了基于最大后验概率准则(Maximumprobability, MAP)的格型SISO均衡器[1]，其均衡性能是最优的，但计算复杂度随信道冲激响应长度呈指数增长。为了降低计算复杂度，提出了更为实用的基于线性最小均方误差估计(Linear Minimum Mean Squared Error, LMMSE)的SISO均衡器。由于先验符号方差的时变特点，即使信道是恒定的，精确的LMMSE均衡器也是时变的，且滤波器系数的计算较为复杂。因而人们提出了一些简化的算法。目前，基于LMMSE的SISO均衡器及其简化算法可分为以下几类：

(1)精确的均衡器[2,3,5]。将译码器的软输出映射成先验符号均值和方差。对滤波窗口内的接收符号序列和先验信息均值序列进行线性处理，得到某个符号的MMSE估计。由于均衡器的系数是先验符号方差的非线性函数，且先验符号方差是时变的。因而需要为每一个符号进行均衡器系数更新，系数的计算复杂度随滤波器长度平方增长。基于精确的LMMSE-SISO均衡器的Turbo均衡性能接近基于MAP-SISO的Turbo均衡，但其计算复杂度在长延迟信道中同样不能接受。如水声信道，其延迟为几十或者上百个符号长度。

(2)近似的LMMSE均衡器[2,3]。为了降低精确的LMMSE均衡器的计算复杂度，在每次迭代中将均衡器系数设为常值。有两种实现方法：一种是混合方法[2]，在计算滤波器系数中对先验符号方差取两种极端的情况，全“1”和全“0”，分别用于Turbo均衡迭代过程的初始阶段和结束阶段，因而LMMSE滤波器的系数在两种恒定的系数中切换；另一种平均方差的近似方法[3]，即将用先验信息方差的时间平均值代替先验信息方差序列，得到时不变的滤波系数。两种方法都是线性复杂度；若利用快速傅里叶变换实现滤波器，则进一步降低为对数复杂度。相对于精确的LMMSE均衡器，两种近似方法在Proakis C信道下的信噪比损失分别为1.18 dB和0.83 dB。

时不变均衡器(包括混合LMMSE均衡器，平均方差LMMSE均衡器和软反馈均衡器)的实现过程中都忽略了先验符号方差的时变性，导致了性能损失。针对信道未知情况下Turbo均衡，文献[14]通过上下文树算法对先验符号方差窗口矢量进行分类，相对于时不变均衡器性能有所改进，其分类过程的初始化阶段需要较长的训练序列，且计算量较大。

为了利用时变的先验符号方差且保证低的计算复杂度，本文提出了符号方差反馈均衡器(Symbol- Variance Feedback Equalizer, SVFE)算法，其推导过程是对精确的MMSE估计进行一阶Taylor展开，表示为符号方差的一次线性函数。SVFE均衡器的处理过程如下：先利用时不变均衡器得到初步符号估计值，用先验符号方差对该估计值加权，进行二次滤波得到更佳的符号估计值，由于用到了时变的先验符号方差信息，因而其性能更接近精确的LMMSE均衡器。在Proakis C信道下，相对于低复杂度的时不变均衡算法，所提出的符号方差反馈均衡算法将信噪比损失从0.83 dB降到了0.17 dB，并且仍可通过快速傅里叶变换降低为对数复杂度。

2 系统描述

在发送端，信息比特进行递归系统卷积码编码，之后进行交织和调制得到个符号。通过带有多径和加性噪声的信道之后，接收符号表示为

在接收端的Turbo均衡处理中，SISO均衡器和SISO译码器进行软信息的迭代。Turbo均衡中信道估计可以采用Turbo迭代估计的方式或者盲估计[15,16]的方式。在本文中认为信道冲激响应是完全已知。基于LMMSE的SISO均衡器实现方法如下：首先，译码器输出的先验对数似然比(LLR)被映射成[2,3]先验符号均值和方差。其次，得到估计值为[2]

且有

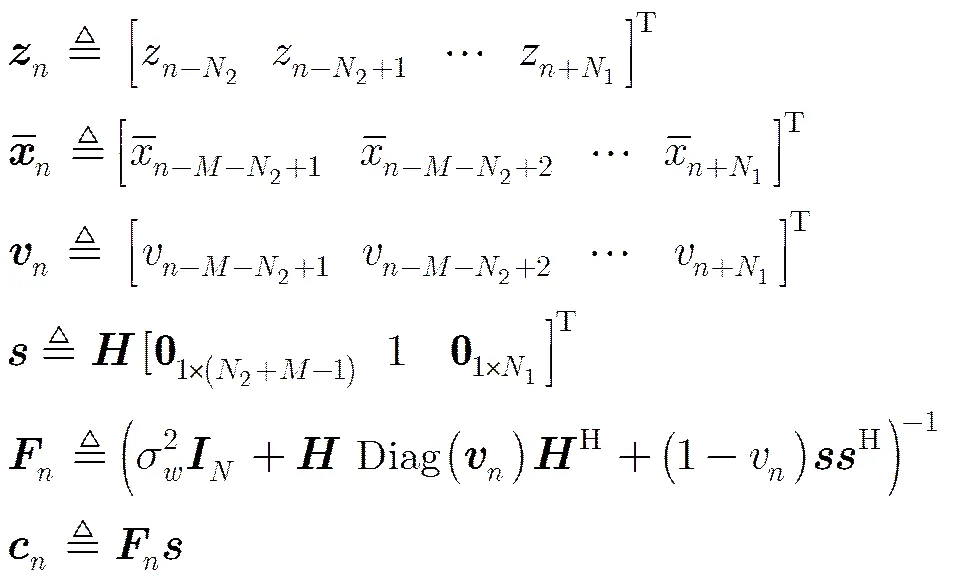
3 符号方差反馈均衡器

为了利用时变的先验符号方差且保证低的计算复杂度，将精确的MMSE估计进行一阶Taylor展开，表示为符号方差的一次线性函数。

3.1 精确MMSE线性估计的Taylor展开

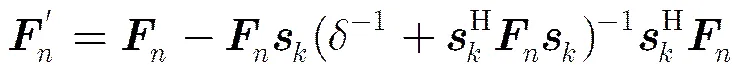
根据偏导数的定义可以得到：

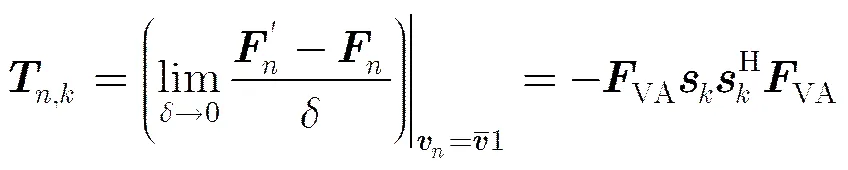
因此，Taylor展开可简化写为

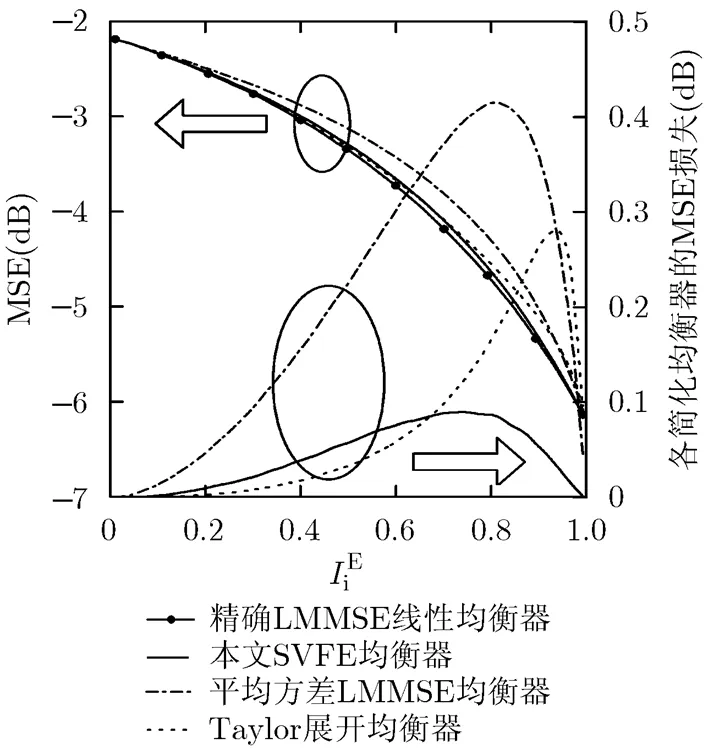
图1 不同均衡器均方误差随外部输入信息

的变化关系(符号信噪比=2 dB)

3.2 符号方差反馈均衡

本文提出的符号方差反馈均衡器(SVFE)的符号估计式为

定义如式(16)所示变量及其矢量形式：

将式(9)，式(12)，式(16)，式(17)，式(18)代入式(15)得到：

图2给出了SVFE均衡器的结构图，其中3个滤波器均为时不变系数。可进一步利用基于重迭保留的分段快速傅里叶变换方法[17]简化计算，复杂度可降低为均衡器长度的对数量级。图1给出了其均方误差性能。得到估计后，输出对数似然比的计算方法与平均方差MMSE线性均衡[3]相同。对于二进制相移键控调制，可得输出对数似然比为

4 仿真结果分析

Turbo均衡的性能进行比较，选取4种SISO衡器：MAP均衡器、精确LMMSE线性均衡器、本文提出的SVFE均衡器和平均方差LMMSE均衡器。仿真条件与文献[3,4,12]相同：信息比特长度为，信道编码码率为，采用生成式为的递归系统卷积码进行编码。编码后的

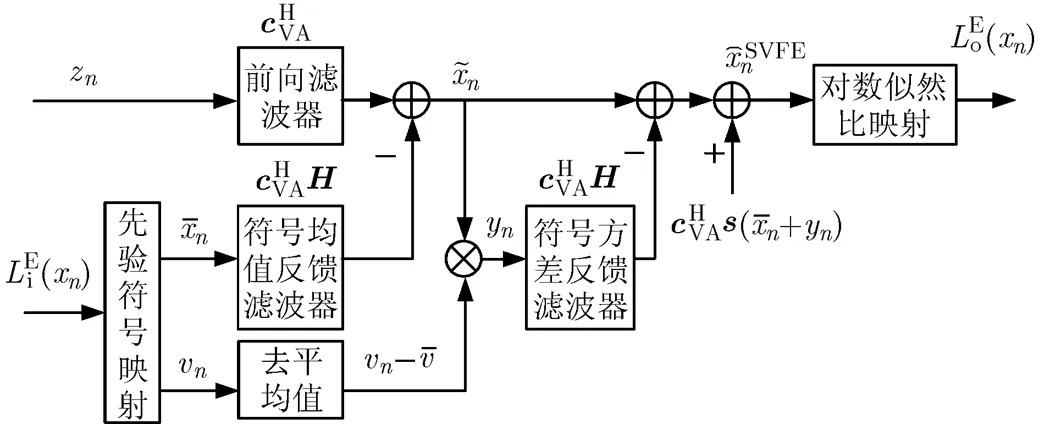
图2 本文提出的符号方差反馈均衡器

图3展示了符号信噪比为2 dB时SISO均衡器的外部互信息转移图(EXIT)[19,20]。相比于精确LMMSE线性均衡器，平均方差LMMSE均衡器输出信息的最大性能损失为0.05，而本文的SVFE均衡器的最大性能损失则明显降低，最大损失为0.004。借助于译码器的外部信息转移图，可以预测，在2 dB符号信噪比下经过足够次数的迭代过程，精确LMMSE线性均衡器和本文SVFE均衡器都可实现较低的误比特率，而平均方差MMSE均衡器不能收敛，误比特率(BER)较高。

图4展示了各Turbo均衡器经过14次迭代之后的误比特码率性能。时，基于精确LMMSE线性均衡器和本文提出的SVFE均衡器的Turbo均衡器，；而平均方差LMMSE均衡器对应的Turbo均衡器，。验证了前文外部互信息转移图的分析。表1给出了4种低复杂度算法的对比。本文提出的算法性能最优，且可以利用快速傅里叶变换实现。

5 结论

本文提出了一种基于MMSE准则的Turbo均衡低复杂度实现方法，即符号方差反馈均衡器(SVFE)。所提出的Turbo均衡方法，将初始估计进行先验符号方差加权后反馈滤波得到更佳的符号估

表 1 不同低复杂度 Turbo 均衡比较

低复杂度均衡器

相对精确MMSE均衡器的SNR损失(BER=0.001)

能否FFT实现

对先验方差的处理

本文提出的均衡器

0.17

能

方差近似为平均值，时变方差反馈

软反馈均衡器

0.33

否

方差近似为平均值，软判决反馈

平均方差均衡器

0.83

能

方差近似为平均值

混合简化均衡器

1.18

能

方差在0和1之间切换

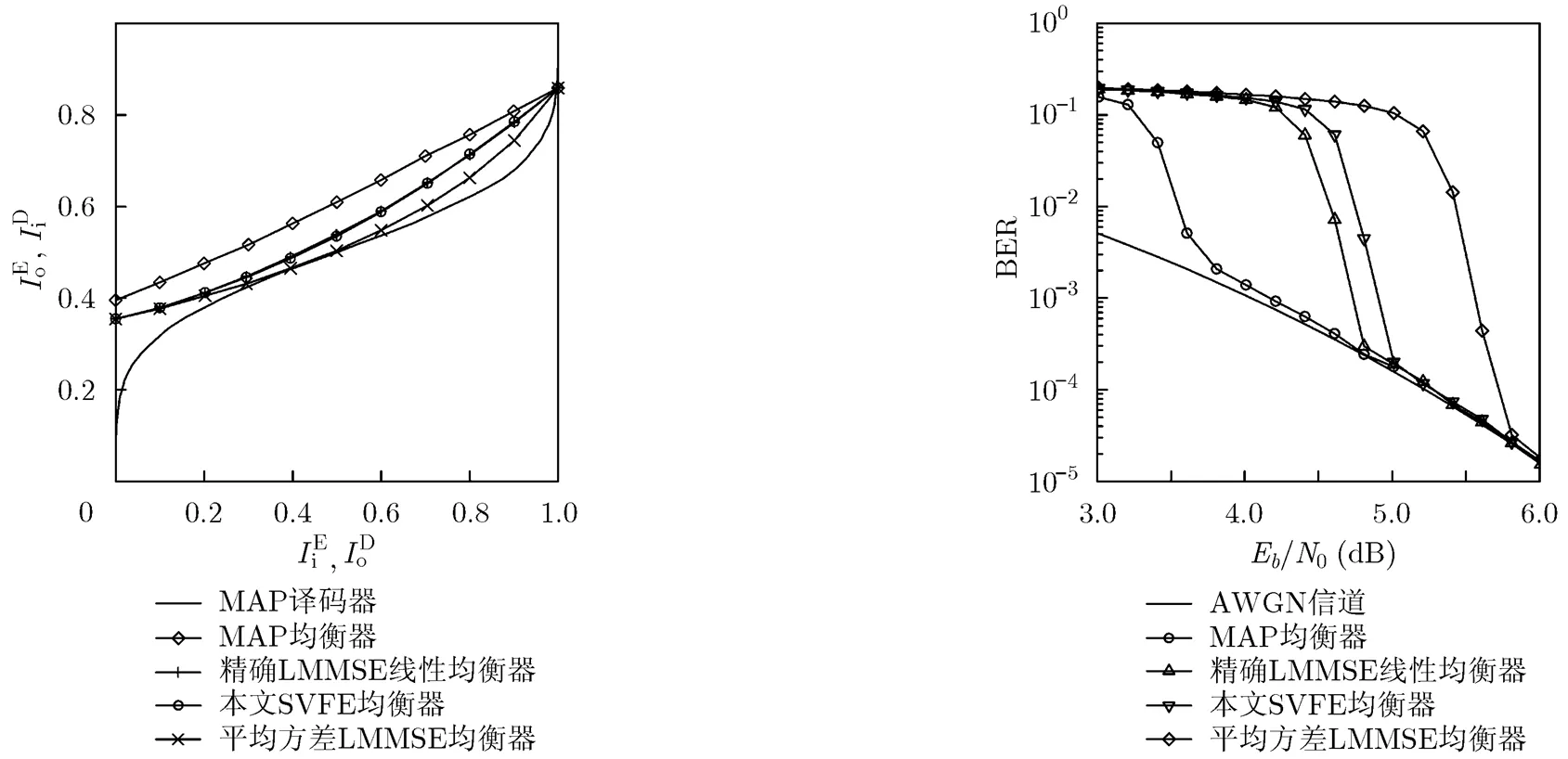
图 3 不同均衡器的外部信息转移图(符号信噪比=2 dB) 图 4 经过14次迭代后各Turbo均衡器的误比特率性能图

计，且可以通过快速傅里叶变换实现。仿真结果显示，在码间串扰严重的Proakis C信道下，相对于精确MMSE线性均衡器，本文提出的均衡器信噪比损失只有0.17 dB。该方法还可用于自适应Turbo均衡[7]、高阶调制Turbo均衡[5,11]及频域Turbo均衡[21]。

[1] DOUILLARD C, JEZEQUEL M, BERROU C,Iterative correction of intersymbol interference: Turbo- equalization[J]., 1995, 6(5): 507-511. doi: 10.1002/ett.4460060506.

[2] TUCHLER M, KOETTER R, and SINGER A C. Turbo equalization: principles and new results[J]., 2002, 50(5): 754-767. doi: 10.1109/TCOMM.2002.1006557.

[3] TUCHLER M, SINGER A C, and KOETTER R. Minimum mean squared error equalization using a priori information[J]., 2002, 50(3): 673-683. doi: 10.1109/78.984761.

[4] LOPES R R. Iterative estimation, equalization and decoding [D]. [Ph.D. dissertation], Georgia Institute of Technology, 2003.

[5] TUCHLER M and SINGER A C.[J]., 2011, 57(2): 920-952. doi: 10.1109/TIT.2010.2096033.

[6] GUO Q and HUANG D.[J]., 2011, 15(5): 566-568. doi: 10.1109/LCOMM.2011. 032811.102073.

[7] LAOT C, GLAVIEUX A, and LABAT J.[J]., 2001, 19(9): 1744-1752. doi: 10.1109/ 49.947038.

[8] STOJANOVIC M and PREISIG J.[J]., 2009, 47(1): 84-89. doi: 10.1109/MCOM.2009.4752682.

[9] SINGER A C, NELSON J K, and KOZAT S S. Signal processing for underwater acoustic communications[J]., 2009, 47(1): 90-96. doi: 10.1109/ MCOM.2009.4752683.

[10] 许浩, 朱敏, 武岩波. 一种水声通信中的多阵元Turbo均衡算法[J]. 电子与信息学报, 2014, 36(6): 1465-1471. doi: 10.3724/ SP.J.1146. 2013.01027.

XU Hao, ZHU Min, and WU Yanbo. An algorithm of multi-array Turbo equalization of underwater acoustic communication[J].&, 2014, 36(6): 1465-1471. doi: 10.3724/SP.J.1146. 2013.01027.

[11] LOU H A and XIAO C S. Soft-decision feedback Turbo equalization for multilevel modulations[J]., 2011, 59(1): 186-195. doi: 10.1109/TSP.2010.2083656.

[12] VOGELBRUCH F and HAAR S. Low complexity Turbo equalization based on soft feedback interference cancelation [J]., 2005, 9(6): 586-588. doi: 10.1109/LCOMM.2005.07016.

[13] 窦高奇, 高俊, 陶伟, 等. 基于序列检测的块判决辅助Turbo均衡器[J]. 电子与信息学报, 2009, 31(9): 2152-2156.

DOU Gaoqi, GAO Jun, TAO Wei,. Sequence-based block decision-aided equalizer for Turbo equalization[J].&, 2009, 31(9): 2152-2156.

[14] KIM K, KALANTAROVA N, KOZAT S S,. Linear MMSE-optimal Turbo equalization using context trees[J]., 2013, 61(12): 3041-3055. doi: 10.1109/TSP.2013.2256899.

[15] 杨晓霞, 王海斌, 汪俊, 等. 水声通信中基于信道辨识的盲Turbo均衡方法[J]. 应用声学, 2015, 34(2): 125-134.

YANG Xiaoxia, WANG Haibin, WANG Jun,. Blind Turbo equalization based on channel identification for underwater acoustic communications[J]., 2015, 34(2): 125-134.

[16] 张冬玲, 杨勇, 李静, 等. 基于Turbo均衡和信道估计的单通道盲信号恢复算法[J]. 通信学报, 2014, 35(1): 47-61.

ZHANG Dongling, YANG Yong, LI Jing,. Blind data recovery of single-channel mixed signals based on Turbo equalization and channel estimation[J]., 2014, 35(1): 47-61.

[17] PROAKIS J G and MANOLAKIS D G. Digital Signal Processing: Principles, Algorithms and Applications[M]. 4th ed, New Jersey: Prentice-Hall, 2007.

[18] PROAKIS J G and SALEHI M. Digital Communications[M]. 5th ed, New York: McGraw-Hill, 2008: 640-672.

[19] LEE S J, SINGER A C, and SHANBHAG N R. Linear Turbo equalization analysis via BER transfer and EXIT charts[J]., 2005, 53(8): 2883-2897. doi: 10.1109/TSP.2005.850375.

[20] MOVAHEDIAN A and MCGUIRE M. On the capacity of iteratively estimated channels using LMMSE estimators[J]., 2015, 64(1): 97-107. doi: 10.1109/TVT.2014.2320928.

[21] 钟凯, 彭华, 葛临东. 基于Rimoldi分解的连续相位调制信号Turbo频域均衡算法[J]. 电子与信息学报, 2014, 36(5): 1190-1195. doi: 10.3724/SP.J.1146.2013.00990.

ZHONG Kai, PENG Hua, and GE Lindong. Turbo frequency domain equalization algorithm based on Rimoldi decomposition for continuous phase modulation signals[J].&, 2014, 36(5): 1190-1195. doi: 10.3724/SP.J.1146.2013.00990.

武岩波： 男，1982年生，副研究员，研究方向为水声通信及组网.

房小芳： 女，1989年生，硕士生，研究方向为通信信号处理.

朱 敏： 男，1971年生，研究员，研究方向为海洋声学.

Foundation Items: The National Natural Science Foundation of China (61471351), The National 863 Program of China (2009AA 093301)

Symbol-variance Feedback Equalizer for Turbo Equalization

WU Yanbo①②FANG Xiaofang②③ZHU Min①②

①(State Key Laboratory of Acoustics, Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China)②(Ocean Acoustic Technology Center, Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China)③(University of Chinese Academy of Sciences, Beijing 100190, China)

A novel Symbol-Variance Feedback Equalizer (SVEF) algorithm is proposed to reduce the computational complexity of the equalizer in Turbo equalization. The derivation of the algorithm is based on the Taylor expansion of the Linear Minimum Mean Squared Error (LMMSE) estimation function. In the proposed scheme, the initial estimates are obtained from the time-invariant equalizer, then the estimates are weighted by thesymbol variances and finally filtered by a time-invariant filter to obtain better estimates. As the time-variantsymbol variances are utilized, the performance of the proposed equalizer is much closer to that of the exact MMSE linear equalizer. Simulation results show that the Signal-to-Noise Ratio (SNR) loss of the proposed scheme in Proakis C channel is reduced to 0.17 dB from 0.83 dB compared to the various time-invariant MMSE Turbo equalization, and its computational complexity can be reduced to logarithmical order by implementation based on the fast Fourier transform.

Turbo equalization; Soft-Input Soft-Output (SISO) equalizer; Minimum Mean Squared Error (MMSE) linear equalizer

TN911.5

A

1009-5896(2016)03-0694-06

10.11999/JEIT150825

2015-07-09；改回日期：2015-12-08；网络出版：2016-02-03

武岩波 wuyanbo@mail.ioa.ac.cn

国家自然科学基金(61471351)，国家863计划(2009AA 093301)