联合稀疏信号恢复的贪婪增强贝叶斯算法

王友华，张建秋

（1.复旦大学电子工程系，上海200433；2.模拟集成电路重点实验室，重庆400060）

联合稀疏信号恢复的贪婪增强贝叶斯算法

王友华1，2，张建秋1

（1.复旦大学电子工程系，上海200433；2.模拟集成电路重点实验室，重庆400060）

本文针对联合稀疏信号恢复问题，提出了一种贪婪增强贝叶斯算法.算法首先利用联合稀疏的特点对信号进行建模，然后在贝叶斯框架下，提出一种贪婪推理方式对信号恢复问题进行迭代求解.在迭代过程中，提出算法利用贝叶斯估计的方差信息来增强支撑恢复的结果，极大地提高了算法对信号恢复性能.理论分析表明：提出算法与同步正交匹配追踪算法具有相同的计算复杂度，远低于其他联合稀疏信号恢复算法.提出方法在具有高恢复精度和较低计算复杂度的同时，兼具贝叶斯方法和贪婪算法的优点.数值仿真验证了理论分析的有效性.

联合稀疏；信号恢复；贪婪算法；贪婪增强贝叶斯算法

1 引言

由于可以用远低于香农采样定理所需的测量来恢复原信号，压缩感知理论一涌现就得到了广泛的关注和研究.稀疏信号恢复是压缩感知领域的一个重要研究方向［1～3］.稀疏信号恢复问题可以分为单测量和多测量压缩感知信号恢复.多测量压缩感知信号恢复问题也称为联合稀疏信号恢复问题.当前，联合稀疏信号恢复问题逐渐成为压缩感知研究领域中的一个重要研究内容［4～8］.联合稀疏信号恢复问题在实际中有着广泛的应用；如：波达角估计［7］、磁共振成像［9］、雷达成像［10］、雷达波形设计［11］等.

与单测量压缩感知信号恢复相比，联合稀疏信号恢复算法可恢复的信号最大稀疏度，随着测量数的增加而增加［4，5］.目前，针对联合稀疏信号恢复问题，存在诸如贪婪算法、基于lp（0＜p≤1）范数最小化方法、子空间方法等几类算法.文献［4，12］提出了一种同步正交匹配追踪算法（S-OMP）.文献［7，13］扩展了l1范数最小化方法，提出了混合范数方法（M-BP）.文献［14］将单测量压缩感知问题中的稀疏贝叶斯学习方法推广到联合稀疏信号恢复问题中，从而提出了M-SBL方法.文献［15～17］将多测量压缩感知问题进行“拉长”处理，将问题转化为单测量压缩感知问题进行求解，利用“块稀疏”的先验，提出了B-OMP方法.文献［6］以阵列信号处理中的MUSIC方法为基础，提出了CS-MUSIC方法.最近，沿着单测量信号恢复的思路，文献［18］将单测量压缩感知中的子空间追踪方法进行扩展，并应用于多测量压缩感知中，提出了GSP方法.文献［19］将单测量压缩感知文章中的贪婪算法统一推广到多测量压缩感知问题中，并对多测量压缩感知问题的相变进行了研究.

前述方法中，贪婪算法和子空间方法具有运算速度快的优点，但是信号恢复性能不如其他方法好.基于lp（0＜p≤1）范数最小化方法和基于贝叶斯推理的算法对信号恢复性能好，但是运算量较大.为了克服目前算法存在运算量和恢复性能折中的问题，本文在贝叶斯框架下，提出了一种新的联合稀疏信号恢复算法，称之为贪婪增强贝叶斯算法（GRBA）.GRBA首先采用稀疏的先验知识对信号的联合稀疏特性进行建模，以便获得更为准确的信号估计.在所建模型基础上，GRBA在贝叶斯框架下，自适应地学习稀疏模型中的超参数.超参数学习过程中，GRBA利用本文提出一种贪婪的策略对信号进行恢复，从而极大的降低了算法的复杂度.同时，GRBA充分利用贝叶斯估计不仅能够得到信号均值信息，还能得到信号方差信息的特点，首次将获得的方差信息对每次估计均值进行增强，极大地提高了算法对支撑恢复的准确性.理论分析和数值仿真表明：GRBA既具有传统贝叶斯方法对信号恢复精度高的优点，又具有贪婪算法运算量小的特点.特别的，GRBA相对于常见的贝叶斯推理算法，由于更充分利用了贝叶斯推理过程得到的均值和方差信息，极大地降低了计算量、提高了信号恢复的精度.

本文的数学符号按照如下规则进行处理：大写黑斜体字母表示矩阵，小写斜黑体字母表示向量.矩阵X的第i行表示为Xi·，第j列表示为 X·j，第 i行、第 j列元素表示为Xij.xi表示向量x的第i个元素.向量x的2-范数表示为‖x‖2.p（x|y）表示给定y时x的条件概率密度函数；p（x；α）表示x满足参数为α的概率密度函数p.N（μ；σ）表示均值为μ，均方差为σ的正态分布.diag（x）表示一对角矩阵，其对角线元素为x.矩阵X的支撑记为supp（X），对于一M×N的矩阵X，其支撑定义为：supp（X）=｛1≤i≤N：‖Xi·‖2≠0｝，|I|表示集合I的非空元素个数.IL表示L×L的单位矩阵，0表示零向量，其长度由上下文确定.

2 问题描述及提出算法

2.1问题描述

联合稀疏信号X∈RN×L可以描述为［6～8］：

其中，W∈RM×L，T∈RM×L和A∈RM×N分别为测量噪声矩阵、观测数据矩阵和测量矩阵.本文假设测量噪声为零均值高斯白噪声.根据观测数据矩阵T和测量矩阵A，联合稀疏信号恢复问题中信号的估计可表示为［6，7］：

式（1）中信号X的最大后验估计为［14］：

当测量噪声W为零均值，方差与λ相关的高斯白噪声，且信号的先验分布为exp（-‖X‖0）时；式（3）和式（2）的解具有相同形式.在信号空间中，先验分布exp （-‖X‖0）在全零处具有最大峰值，能够很好地描述信号的稀疏特性.但是，与该信号先验相对应的式（2）却存在大量的局部最优解［14］.因此，研究者希望找到一种稀疏的先验，既能对信号的稀疏性进行描述，又能避开局部最优解.而层次化的先验具有上述的特征.

本文设信号X的第i行Xi·（1≤i≤N）满足层次化的先验分布［20～22］；其中，第一层为零均值高斯分布：

其中γi是信号第i行高斯分布的方差.由式（4）知，当方差γi为零时，信号X的第i行 Xi·为零的概率是1.进一步，当未知的方差γi满足平移截断伽马分布时，得到先验分布的第二层为［22］：

其中γ=［γ1，…，γN］T，概率分布密度函数Γτ（γi；ε，η）定义为：

式中，形状参数ε、变化率η和平移τ等参数均大于零；式（6）等号右侧分母中伽马函数Γητ（ε）定义为：

式（4）与式（5）所定义的层次化先验分布推广了高斯-伽马分布［20］和拉普拉斯先验分布［21］，它们能够对信号稀疏性进行更好的描述.在先验分布的第二层次，由于未知方差参数γi（i=1，…，N）满足独立平移截断的伽马分布，有：

由式（8）可以看出：当 ε＜1时，γi以极大的概率为零；由先验分布的第一层次知，此时Xi·以极大的概率为零.因此，这样的层次化先验分布可以很好地描述信号X的联合稀疏特性.进一步，设变化率参数η满足先验分布：

易证明：当τ，ε→0时，X的先验分布在零处具有无穷大概率.上述分析表明：利用上述先验分布得到的最大后验估计，能够非常好的表示信号的稀疏解，即能够很好的逼近式（2）.

2.2贝叶斯推理算法

由式（4）定义的信号X每行先验分布；可得：当给定参数γ时，信号X的每列都为零均值的高斯分布.设信号X全部列的协方差矩阵记为Γ，则有：Γ=diag（γ1，…，γN）.设测量噪声W的方差为σ2，由测量方程式（1）知，当给定观测数据矩阵T时，X的第j列X·j（1≤j≤L）后验分布为：

经过计算，X第j列X·j（1≤j≤L）的后验分布为：

其中：

由式（11）知，该后验分布为高斯分布.将 X的所有列写成矩阵形式，得到X的后验分布为：

其中，均值矩阵Π和方差矩阵Σ分别为：

矩阵C定义为：

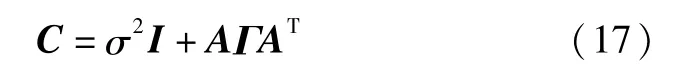
当超参数γ已知时，均值矩阵Π可作为信号X的估计值 ^X.通过式（15），将信号X的估计问题转化成为对超参数γ的估计问题.

（1）超参数估计

由于不同的超参数γ对应不同的先验分布，不同的先验分布又决定了信号非零行的位置，从而决定测量矩阵A中对测量数据T起作用的列.因此：确定合适的超参数γ等效于根据已知测量数据矩阵T来选择测量矩阵A中不同的列（基）.在贝叶斯框架下，可将X作为隐变量，将其积分掉［23］，从而可完成对γ的估计.当c= d=0时，将log（η）作为隐变量，可以得到下面关于γ和log（η）的对数似然函数：

其中c1为常数.将式（17）代入式（18）中，可得到γ的似然函数；对其关于γi求导，可得：

其中：

令式（21）为零，即可求得γi.由式（20）知，f（t）的系数与方差矩Σ和均值矩阵Π相关.因此，γi与方差矩阵Σ和均值矩阵Π相关.而由式（15）和（16）知：方差矩阵Σ和均值矩阵Π又与超参数γ相关.因此，可以采用迭代方式对γ、Σ、Π进行求解.式（21）中一元三次方程的三次项系数和二次项系数均大于零，常数项小于零.由附录中一元三次方程求根引理一可知：f（γi）=0存在一正实根，记为则似然函数 L（γ，log（η））在处取得最大值.同理，可求得参数η的估计值.当求得γ估计值后，由式（15）和式（16）可以求得矩阵Σ和Π；从而可以进行下次迭代，直至满足终止条件.

（2）噪声方差估计

在上述分析中，假设测量噪声W的方差σ2是已知的.当σ2未知时，将噪声方差σ2作为参数，利用EM算法［24］，对σ2进行迭代求解，在每次迭代中，σ2的估计为：

3 贪婪推理方法

在前述贝叶斯推理过程中，每次迭代需对式（15）中的矩阵C求逆.当信号维度较大时，矩阵求逆将带来很大的运算量.针对该问题，本节在前述框架下，提出一种贪婪的推理方法来进行贝叶斯估计.由于信号X是联合稀疏的，即参数γ只有较少的非零元素.由式（15）知，均值矩阵Π也只有较少非零行.这表明在计算Σ和Π时，可以只针对非零的γi进行计算，以达到降低计算中Σ和Π维度的目的.基于这个思路，本文首先从γ= 0开始，通过贪婪方式逐渐将非零γi加入到模型中.因此在整个计算过程中，Σ和Π的实际维度都较小.为了避免复杂的记号，设测量矩阵A按列分块为A=［a1，a2，…，aN］.

对式（17）中C作如下变换：

其中C-i为C中不含ai和γi的部分.将式（23）其代入式（18），可得：

式中c1和c3为常数.通过式（24），将对数似然函数L（γ）分成两部分：与ai及γi不相关的部分L（γ-i），与ai及γi相关的部分l（γi）.l（γi）定义为：

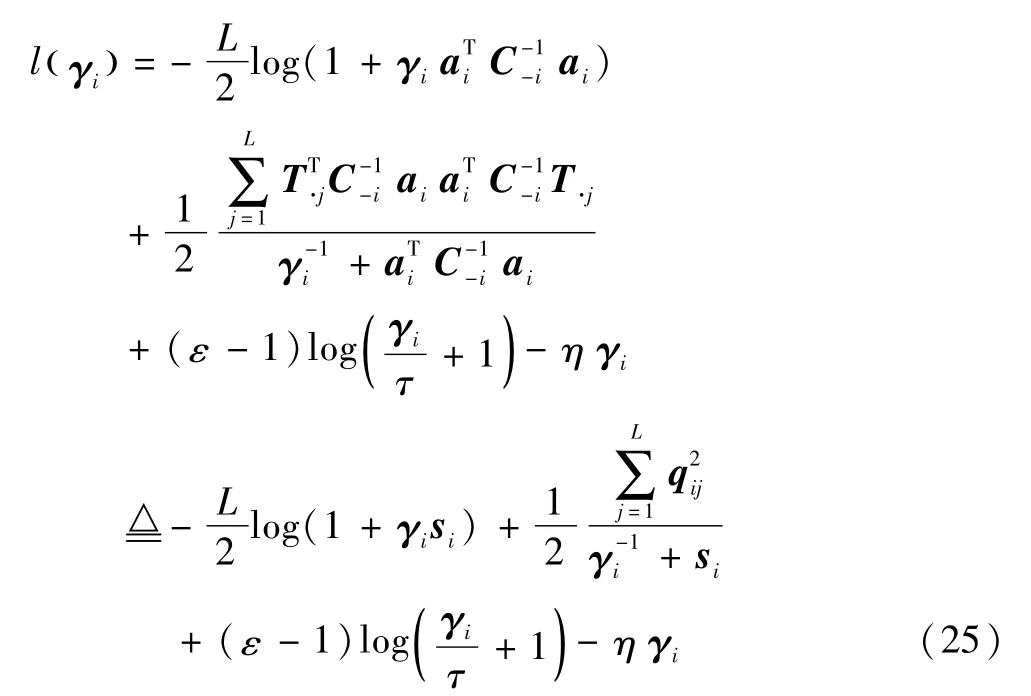
其中，si，qij分别为：

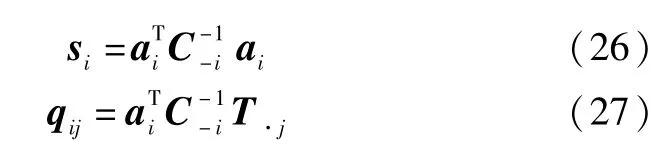
由于矩阵C-i和C-1-i均为正定矩阵，信号采样快拍数L ≥1，si＞0（i=1，…，N）.因此式（29）中系数c1，c2＞0.利用附录所述的一元三次方程求根基本知识，下面分三种情况来讨论 l（γi）在何处取得最大值.

（1）c4＜0.由引理一知h（γi）=0在（0，+∞）上有唯一的解，设为容易证明l（γi）在上单调上升，在上单调下降.因此处取得最大值，即

（2）c4≥0，c3＜0，Δ＞0.因为Δ＞0，由引理二知，存在三个不同的实根.由于表示函数h（γi）关于γi的导数）且c3＜0，所以h（γi）在y轴的两边各有一驻点.由于h（0）= c4≥0，所以三个不同实根包含一个负实根和两个正实根.令为最大实根，则l（γi）从零点处到某点单调下降，然后从某点到l（γi）处单调上升，接着单调下降.故：l（γi）要么在零点处获得最大值，要么在处获得最大值.因此：如果，则处获得最大值，则；如 果，则l（γi）在零处获得最大值，则

上述分析表明：通过对一元三次方程求解和逻辑判断可保证每次迭代后似然函数都在不断的增加；通过迭代更新γi，以确定测量矩阵A中第i列ai是否对应信号的非零行.在迭代求解过程中，设前次迭代的γi值记为取得最大值处对应的自变量为如果则表明基矢量ai对增加似然函数是有贡献的，应将其纳入到模型中，同时更新如果，则表明基矢量ai已存在于模型中，只需要更新γi的值为当前迭代值即可.如果则表明基矢量ai对增加似然函数无贡献，当前的迭代应该将其从模型中删除，同时令完成γ的一次迭代后，更新参数η.

上述迭代过程可以从空集开始，逐渐将基矢量ai添加到模型中，或者从模型中删除，直到收敛.迭代过程仅需求解一元三次方程和作简单的逻辑判断，不需要进行高维矩阵求逆，从而极大地降低了算法的复杂度.与文献［25］类似，为了更高效地更新式（26）和式（27）中的参数si、qij，令：

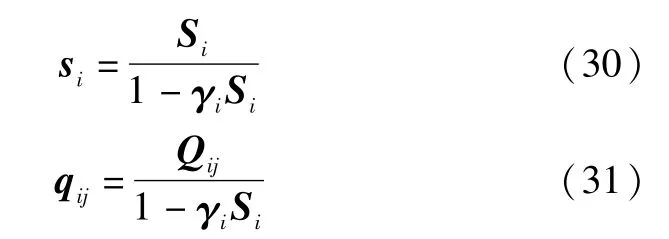
其中

上式中Σactive和Aactive仅包含γi≠0对应的ai所构成的方差矩阵和测量矩阵.由于信号具有联合稀疏特性，所以γ中非零元素非常少.因此，Σactive和Aactive的维度是很小.故对式（32）和式（33）进行计算只需要较小的计算量.详细的计算量分析见算法复杂度部分.

4 贝叶斯增强

传统基于贝叶斯方法的联合稀疏信号恢复算法［20～22］，仅仅利用了后验分布的均值信息，并将其作为信号的估计值.但是贝叶斯估计方法不仅能得到估计的均值信息，也能够得到方差信息.但是，除文献［26］以外，尚未有其他的文献利用该信息.文献［26］将方差信息作为自适应设计测量矩阵的一种度量，并未讨论如何利用方差信息来提高恢复算法本身的性能.本文将提出一种增强方法，它将利用方差信息来提高算法对支撑估计的正确率.由测量方程式（1）可知，X·j，T·j构成的评价函数为：

因此，其Fisher信息矩阵为［24］：

设信号和测量噪声不相关，有：

将式（36）至式（38）代入式（35），可得到：

不失一般性，设测量矩阵A为列归一化的矩阵，可得：

因此：

由于Δ中元素较小，因此式（42）表示：对任给的列信号，其估计的克拉美劳下限约为噪声功率.基于前述推导，算法在每次迭代过程中，根据当前的方差矩阵和噪声估计值进行判断.如果方差矩阵的某一（些）对角元素Σii，远远比噪声方差小；即可认为，与Σii相对应的γi值较小，其估计的可信度不高.与之对应的基向量ai不应在信号生成模型Aactive中.如果在迭代过程中，该基向量已经在Aactive中；那么当前迭代中应该将其删除.

5 算法复杂度分析

本文提出算法计算量主要在对式（29）至（33）的计算及做相应的逻辑判断上.由前述分析知：Σactive列数在每次迭代过程中动态增加，但是最多为K列（K为X中非零行数）.因此，最坏情况下计算Σactive需要O（K2M）+O（K3）次操作.由于K＜M，Σactive计算仅需要O（K2M）次操作.在计算Qij时，需要O（MK）操作.因此，在每次迭代过程中，更新完所有的Qij时，需要O（MKNL）次操作.因此本文提出算法的复杂度与S-OMP方法的算法复杂度相当［12］.由文献［14］知，M-SBL每次迭代需要的算法复杂度为O（M2NL），用标准二阶锥实现的M-BP算法的复杂度为O（N3L3）.由于在联合稀疏问题中K＜＜M ＜＜N，因此，本文提出算法的复杂度远远小于其他方法的算法复杂度.

6 仿真结果

本节在仿真中，除GRBA的性能外，还列出了S-OMP［12］、B-OMP［15］、M-BP［7，13］、M-SBL［14］及CS-MUSIC［6］的性能.在仿真中，信号相对均方误差（RMSE）定义为：

本节通过仿真，将验证贝叶斯推理过程中方差矩阵对角元素分布情况.在仿真中，噪声方差 σ2=0.01. 图1表示了没有增强时，方差矩阵Σ对角元素分布情况.图中x-轴为信号X的行号，y-轴为估计的方差值.

图中星号点为非零行对应的方差值.从图1中可以看出，当无增强时，算法共恢复出了31个非零行；其中第183行被错误地恢复成信号的支撑.从图中可以看到正确支撑所对应的方差值集中在σ2附近.与第183行对应的方差明显小于其他行所对应的方差值.因此，可以通过前述的贝叶斯增强方法，提高算法对支撑正确恢复的概率.

图2为本文提出算法有增强和无增强两种情况下，支撑恢复率对比.在仿真中，信号非零行数从26到45均匀变化，其余仿真参数设置同上一仿真设置.

图2中，菱形线为有方差增强时的支撑回复率，星号线为算法无方差修正时的结果.从图中可知，当算法采用方差增强时，可以大幅度的提高算法对支撑的恢复率.特别是在低稀疏度时，两者具有较大的差距.在下文中，GRBA方法的仿真结果均是指具有方差增强时算法的性能.本小节给出了算法性能随着信噪比变化的趋势.在仿真中，信噪比从12dB到30dB均匀变化.

图3所示为算法的支撑恢复率与信噪比关系.从图中可以看到，当信噪比大于一定“阈值”后，GRBA方法和M-SBL方法对支撑恢复性能迅速提高.对于GRBA方法，该“阈值”约为13dB；对于M-SBL方法，该“阈值”约为25dB.因此，GRBA对测量噪声敏感性远低于MSBL方法.同时，由图3知：CS-MUSIC方法的支撑恢复率随着信噪比的增加而线性增加；但是增加的速度较慢.两种贪婪的恢复算法：S-OMP和B-OMP方法在仿真的信噪比区间均不能正确的恢复信号支撑.

图4所示为信号的均方误差与信噪比关系.从图中可以看到，基于统计推理的算法对信号幅度恢复明显优于确定性算法.在所有算法中，GRBA方法幅度恢复性能最优，CS-MUSIC方法对幅度恢复性能最差.在低信噪比区域，由于GRBA和M-SBL对支撑恢复率均较低，因此两者间的差距较小.随着信噪比的增加，GRBA对支撑成功恢复率迅速增加，而M-SBL对支撑恢复率仍然较低；因此，GRBA和M-SBL之间的差距拉大.随着信噪比的进一步增加，GRBA和M-SBL均能够以极高的概率恢复信号支撑，此时GRBA和 M-SBL之间的差距缩写.从图中可以看到，两种贪婪的恢复算法：S-OMP方法和B-OMP方法对信号幅度恢复差别较小.

图5所示为算法运行时间随着信噪比变化曲线.图5上图为所有算法运行时间的对比图.从上图可以看到，M-BP算法的运算时间最长，远远高于其他的算法运行时间；其次为M-SBL方法，算法S-OMP方法的运行时间最短.图5下图显示了GRBA方法、B-OMP方法、SOMP方法和CS-MUSIC方法的运行时间.从图中可以看到，虽然本文提出的GRBA方法为基于贝叶斯推理的恢复方法；但是采用了贪婪推理方法，运算时间不仅仅远低于同样为统计推理的M-SBL方法；还低于贪婪算法B-OMP的运行时间，和贪婪方法S-OMP的运行时间相似.且随着信噪比的增加，GRBA运行时间和S-OMP方法运行时间的差距越来越小.从图中看到，随着信噪比的减少，噪声功率增加；M-SBL方法迭代次数增加，运行时间变长.而GRBA方法采用估计方差信息增强，将估计方差和估计噪声功率进行比较，能自适应地估计信号的支撑.因此，与M-SBL方法相比，其运行时间随着信噪比变化波动较小.另外，从图5中可以看到，同为贪婪算法，B-OMP方法运行时间较S-OMP方法运行时间长.造成这种情况是因为：B-OMP在求解过程中，将多测量压缩感知问题转化成单测量压缩感知问题，将信号X和测量数据T进行“拉长”处理，极大的增加了求解问题的维度，增加了算法运行时间.

当改变信号快拍数、信号稀疏度时，算法取得了与前述类似的性能，由于篇幅限制，本文没有将其性能一一列出.

7 结论

本文针对联合稀疏信号恢复问题，提出了一种增强贝叶斯信号恢复算法.算法在贝叶斯框架下，采用了一种贪婪的方法和一种增强的策略对信号稀疏模型进行求解.从而使本文提出方法既具有贝叶斯方法恢复精度高的优点又具有贪婪算法运算量小的特点.理论分析和数值仿真结果证明了提出算法的良好特性.

附录

引理二［28］对一元三次方程令其判别式为：

如果Δ＞0，则g（t）=0有三个不同的实根；如果Δ =0，则方程有三个实根，其中包含重根；如果Δ＜0，则方程包含一实根和一对共轭复根.

［1］D L Donoho.Compressed sensing［J］.IEEE Trans on Information Theory，2006，52（4）：1289-1306.

［2］E Candes，T Tao.Decoding by linear programming［J］. IEEE Trans on Information Theory，2005，51（12）：4203 -4215.

［3］焦李成，杨淑媛，刘芳，侯彪.压缩感知回顾与展望［J］.电子学报，2011，20（7）：1651-1662. JIAO Li-cheng，YANG Shu-yuan，LIU Fang，HOU Biao. Development and prospect of compressive sensing［J］.Acta Electronica Sinica，2011，20（7）：1651-1662.（in Chinese）

［4］J Chen，X Huo.Theoretical results on sparse representations of multiple measurement vectors［J］.IEEE Trans on Signal Processing，2006，54（12）：4634-4643.

［5］P Feng.Universal Minimum-Rate Sampling and Spectrum-Blind Reconstruction for Multiband Signals［D］.Champaign：University of Illinois，1997.

［6］J M Kim，et al.Compressive MUSIC：A missing link between compressive sensing and array signal processing［J］.IEEE Trans on Information Theory，2012，58（1）：278 -301.

［7］D Malioutov，et al.A sparse signal reconstruction perspective for source localization with sensor arrays［J］.IEEE Trans on Signal Processing，2005，53（8）：3010-3022.

［8］M F Duarte，et al.Distributed compressed sensing of jointly sparse signals［A］.Asilomar Conference on Signals，Systems and Computers［C］.USA：Asilomar，2005.1537 -1541.

［9］O Lee，et al.Compressive diffuse optical tomography：noniterative exact reconstruction using joint sparsity［J］.IEEE Trans on Medical Imaging，2011，30（5）：1129-1142.

［10］周汉飞，李禹，粟毅.基于压缩感知的多角度SAR特征提取［J］.电子学报，2013，41（3）：543-548. ZHOU Han-fei，LI Yu，SU Yi.Multi-aspect SAR feature extraction based on compressive sensing［J］.Acta Electronica Sinica，2013，41（3）：543-548.（in Chinese）

［11］贺亚鹏，朱晓华，等.噪声干扰背景下压缩感知雷达波形优化设计［J］.电子学报，2014，42（3）：469-476. HE Ya-peng，ZHU Xiao-hua，et al.Waveform design for compressive sensing radar in the presence of interference and noise［J］.Acta Electronica Sinica，2014，42（3）：469-476.（in Chinese）

［12］J A Tropp，A C Gilbert，M J Strauss.Algorithms for simultaneous sparse approximation，Part I：Greedy pursuit［J］. Signal Processing，2006，86（3）：572-588.

［13］J A Tropp.Algorithms for simultaneous sparse approximation，Part II：Convex relaxation［J］.Signal Processing，2006，86（3）：589-602.

［14］D P Wipf.Bayesian Methods for Finding Sparse Representations［D］.San Diego：University of California，2006.

［15］Y C Eldar，P Kuppinger，et al.Block-sparse signals：uncertainty relations and efficient recovery［J］.IEEE Transa on Signal Processing，2010，58（6）：3042-3054.

［16］R G Baraniuk，V Cevher，et al.Model-based compressive sensing［J］.IEEE Trans on Information Theory，2010，56 （4）：1982-2001.

［17］Y C Eldar，M Mishali.Robust recovery of signals from a structured union of subspaces［J］.IEEE Trans on Information Theory，2009，55（11）：5302-5316.

［18］J M Feng.Generalized subspace pursuit for signal recovery from multiple-measurement vectors［A］.Proceedings of IEEE Wireless Communications and Networking Conference［C］.Shanghai：IEEE，2013.2874-2878.

［19］J D Blanchard，M Cermak，et al.Greedy algorithms for joint sparse recovery［J］.IEEE Trans on Signal Processing，2014，62（7）：1694-1704.

［20］N Pedersen，D Shutin，et al.Sparse Estimation Using Bayesian Hierarchical Prior Modeling for Real and ComplexModels［OL］.http：//arxiv.org/pdf/1108. 4324v2，2011.

［21］S Babacan，R Molina，et al.Bayesian compressive sensing using Laplace priors［J］.IEEE Trans on Image Processing，2010，19（1）：53-63.

［22］Z Yang，L H Xie，C S Zhang.Bayesian Compressed Sensing With New Sparsity-Inducing Prior［OL］.http：//arxiv.org/pdf/1208.6464v1，2012.

［23］D J C MacKay.Bayesian interpolation［J］.Neural Computation，1992，4（3）：415-447.

［24］M R Gupta，Y H Chen.Theory and use of the EM algorithm［J］.Foundations and Trends in Signal Processing，2011，4（3）：223-296.

［25］M Tipping，A Faul.Fast marginal likelihood maximisation for sparse Bayesian models［A］.Proceedings of the 9th International Workshop Artificial Intelligence and Statistics ［C］.Florida：Key West，2003.1-13.

［26］S Ji，Y Xue，L Carin.Bayesian compressive sensing［J］. IEEE Trans on Signal Processing，2008，56（6）：2346 -2356.

［27］Y C Eldar，G Kutynoik.Compressed Sensing［M］.Cambridge：Cambridge Press，2012.

［28］R Irving.Integers，Polynomials，and Rings：A Course in Algebra［M］.Berlin：Springer Verlag，2004.

王友华 男，1981年生，重庆人.2011年进入复旦大学电子工程系，现为博士生，从事压缩感知信号恢复，混合信号集成电路设计等工作.

E-mail：wangyouhua@fudan.edu.cn

张建秋 男，1962年生于湖南隆回县，现任复旦大学电子工程系教授、博士生导师、IEEE高级会员，主要研究领域有信息处理理论及其在测量和仪器、新型传感器、控制和通信中的应用.

E-mail：jqzhang01@fudan.edu.cn

A Greedy Refinement Bayesian Approach to Joint Sparse Signal Recovery

WANG You-hua1，2，ZHANG Jian-qiu1

（1.Department of Electronic Engineering，Fudan University，Shanghai 200433，China；2.Science and Technology on Analog Integrated Circuits Laboratory，Chongqing 400060，China）

In this paper，a new greedy refinement bayesian approach（GRBA），used to solve the joint sparse signal recovery problem，is proposed.The joint sparse property of signals is first used to model the signals.Based on the model，a greedy Bayesian inference method used to estimate the signals is then presented.In order to enhance the performance of the recovery，the covariance matrix got by the Bayesian inference is utilized to refine the support recovery results in our inference process.The analytical results show that GRBA outperforms the reported algorithms in the literature in terms of both the signal recovery accuracy and computational complexity.It keeps both the advantages of Bayesian methods and greedy methods. Numerical simulations verify the effectiveness of the analytical results.

joint sparsity；signal recovery；greedy algorithm；greedy refinement Bayesian approach

TN919.72

A

0372-2112（2016）04-0780-08

电子学报URL：http：//www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.04.005

2014-08-18；

2014-12-14；责任编辑：孙瑶

国家自然科学基金（No.61171127，No.61571131）；模拟集成电路重点实验室基金（No.9140C090110130C09003）