高斯粒子流滤波器
张宏欣,周穗华,冯士民
(海军工程大学兵器工程系,湖北武汉 430033)
高斯粒子流滤波器
张宏欣,周穗华,冯士民
(海军工程大学兵器工程系,湖北武汉 430033)
粒子流滤波器以粒子流速度场描述随机样本从先验分布到后验分布的演化,实现对系统状态的贝叶斯估计.针对其一般解计算复杂、难于滤波求解的问题,导出一种高斯假设条件下的粒子流滤波器.在线性高斯条件下推导了速度场的解析解;证明了当演化步长趋近于0时,该解析解与Kalman-Bucy滤波器的解具有一致的形式;基于该解导出了非线性高斯系统速度场的表达式,并进一步利用Unscented变换近似求解.通过若干仿真算例表明,高斯粒子流滤波器放宽了系统噪声为高斯型的限制,其精度优于经典非线性高斯滤波器,计算复杂度低于一般粒子滤波器,且具有良好的稳定性.
非线性滤波;贝叶斯估计;粒子流滤波器;速度场;Unscented变换
1 引言
贝叶斯非线性滤波基于非线性动态系统模型,通过带噪声的观测采样序列近似计算出目标状态的后验分布统计量,来实现对系统状态的估计[1],近几十年来已经在目标跟踪、导航等工程领域得到了广泛应用.根据近似方法的不同,可分为解析近似方法和仿真近似方法.解析法基于卡尔曼滤波器(Kalman Filter,KF)框架,假设后验分布为高斯型,近似计算非线性变换后的状态均值和误差矩阵,利用卡尔曼滤波框架进行求解,其中,扩展卡尔曼滤波(Extended Kalman Filter,EKF)基于一阶伪线性化,对于高阶模型精度不高;以无迹卡尔曼滤波(Unscented Kalman Filter,UKF)为代表的σ点卡尔曼滤波器[2,3]采用一组确定的样本点更精确的捕捉均值和方差信息,对高斯分布可达到三阶精度;但对于某些高阶模型(如指数函数,三角函数等),在高维情况下仍可能引入较大误差,而捕捉更高阶矩信息则需要更庞大的Sigma点集和克服数值问题[4].
仿真近似方法采用大量随机样本经过特定“变换”来近似后验分布.粒子滤波[5](Particle Filter,PF)从建议分布中抽取满足后验分布样本(重采样),但并未改变样本本身,因此建议分布样本需足量覆盖后验分布样本,否则将导致滤波性能不稳定甚至发散[6],该问题在状态维数较高时尤为明显,通常需要大量随机样本(随问题维数呈指数增长[7]).针对此问题,反馈型的粒子滤波算法通过对每个先验分布样本叠加反馈量来构造建议分布样本,普遍做法是对每个样本进行非线性卡尔曼滤波,从而衍生出EKF-PF及UKF-PF[8]滤波器,这类算法的时间复杂度较高,且在重要性权值计算中很容易出现数值不稳定情况.
粒子流滤波器[9~12](Particle Flow Filter,PFF)是一种无需构造建议分布和重采样过程的反馈式粒子滤波器,通过构造同伦(Homotopy)函数,将先验分布粒子到后验分布粒子的变化过程描述为粒子的“流动”,结合描述概率分布随时间变化的Fokker-Planck方程(FPE),得到粒子流速度场(以下简称速度场)的偏微分方程,求出速度场即可利用数值方法得到后验分布样本;其优势在于无需构造建议分布和重采样过程,且适于求解高维问题[6].文献[9]中通过直接求解泊松方程给出了粒子流速度场理论表达式的Monte-Carlo (MC)积分解,其计算复杂度过高,难于实现.
与文献[9]不同,本文从粒子流滤波器的基本理论出发,推导出一种高斯型粒子流滤波器(Gaussian Particle Flow Filter,GPFF).假设系统噪声为高斯分布的基础上,根据速度场所满足的偏微分方程,在线性高斯条件下推导了速度场的解析解,证明了该解与连续时间条件下的Kalman-Bucy滤波解具有一致的形式;并将该解推广到非线性系统,推导了速度场的期望形式解,结合无迹变换(Unscented Transform,UT)进行近似求解.由于GPFF采用粒子进行非线性传播,放宽了对系统噪声的高斯型限制[13],相比EKF和UKF而言具有较高的精度;保留了PFF无需构造建议分布及重采样的优点,相对PF来讲降低了所需的粒子数量,减小了计算量,且稳定性得到提高.通过对若干问题模型进行仿真验证了GPFF的有效性.
2 反馈粒子滤波器
考虑如下滤波问题模型:




若将状态向量x视为R Rd空间标准基下的某一点的位置坐标,则f(x,λ)可以看做λ时刻该点上的速度,若f对所有粒子都有定义,则它表示粒子从先验分布到后验分布“流动”的速度场.因此,若能求得f,即可通过数值积分方法计算后验粒子.
假设变化过程不存在噪声,根据连续时间随机滤波理论,q(x,λ)满足零扩散项(diffusion term)的Fokker-Planck方程:

其中▽·为散度算子.对式(4)取自然对数得,

对式(7)求关于λ的偏导数,并结合式(6)可得:


式(9)是难处理的,这是因为:(a)获得合适的β值是困难的[9];(b)q(x,λ)求值需要采用分布拟合算法,计算代价过高;(c)格林公式仅适用于d>2情况;(d)已经证明[14],这种形式的解在数值上是不稳定的.因此需要寻求其他方法.事实上,文献[9]中仅给出了使用式(9)计算速度场的结果,并未给出基于该式的滤波结果.
3 粒子流速度场在线性高斯条件下的解
3.1解析解推导
对于线性系统,假设先验概率密度 g(x)满足高斯分布;似然函数h(x)为高斯型,即



分别为λ条件下的后验均值及协方差矩阵.在线性高斯条件下,设粒子流速度场f(x,λ)具有如下形式
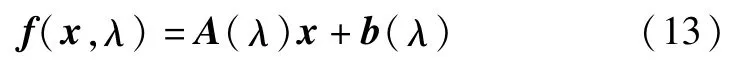
其中A(λ)∈R Rd×d,b(λ)∈R Rd.记f=f(x,λ),注意到式(8)右端的形式,则可将其重写为

将式(11)、(12)和(14)代入式(8)可得:


可得

根据式(18)右端的形式,可设

将式(19)和(20)代入式(15),可以得到如下关系


为减小计算量,利用如下关系
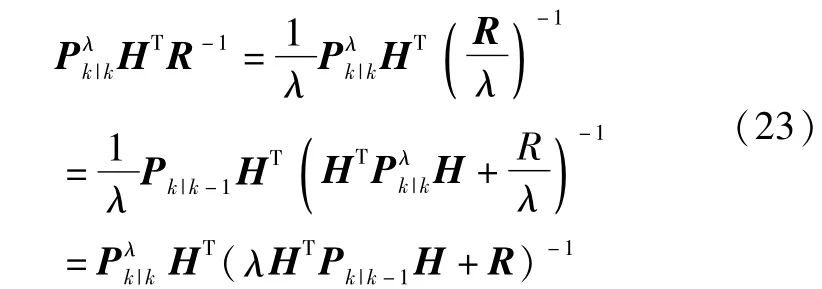
则A(λ)可仅由先验协方差矩阵表示如下


将式(25)和式(26)代入式(20),则b(λ)可仅由先验信息表示为

式(13)、(24)和(27)给出了粒子流速度场在线性高斯条件下的解析解.
3.2速度场与Kalman-Bucy滤波器的一致性
由考虑如下的连续时间线性随机系统

其中xt为连续时间状态向量,Ft为漂移项;Ht为观测矩阵,wt,vt分别为满足零均值的高斯过程的状态噪声和观测噪声,且
对于连续时间线性高斯系统,Kalman-Bucy滤波器[16]以线性微分方程形式给出了最小均方无偏估计解及其协方差矩阵Pt,即


利用式(26)求Pλ关于λ的导数,可得



ε为一任意小的正数.将式(37)代入式(36),化简得

利用式(23),得到Pλ关于λ的导数为

对式(22)取关于x的期望可得,

综上可知线性高斯条件下λ变化过程中,速度场与零漂移项和零过程噪声系统的Kalman-Bucy滤波器解是一致的.
4 非线性滤波
设非线性条件下速度场的解具有如下形式:

将h(x)在状态预测值^xk|k-1附近做一阶泰勒展开,即


将式(41)和式(42)代入式(14),利用2.1节的推导过程可得

为将式(43)表示为统计量形式,利用式(23),并注意到



其中

式(41)和(46)给出了速度场在非线性高斯条件下的近似解.
采用无迹变换(UT)近似求解式(44)及式(45),UT通过一组确定的采样点来近似计算随机变量经过非线性变换后的均值和方差,首先生成Sigma点以及相应用于计算均值的权值和用于计算方差的权值即:

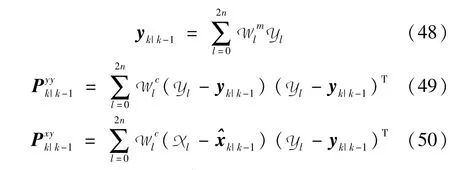
关于状态的统计量直接通过粒子实现,则先验统计量为

其中x(i)k|k-1为第i个先验粒子,N为粒子个数.利用导出的速度场计算公式,对状态在λ∈(0,1]内进行数值积分即可求出后验粒子,相应的后验统计量可根据式(51)和(52)类似地得到.
5 仿真结果及分析
为验证 GPFF的有效性,对三个典型算例,即连续Wiener过程加速度(CWPA)模型、一维非稳定增长(UNG)模型以及只测角跟踪(BOT)模型进行仿真,CWPA模型为线性模型,用于在高斯噪声和非高斯噪声条件下将GPFF与KF进行比较;UNG模型用于在精度上将GPFF与EKF、UKF及PF等经典非线性滤波器进行比较.BOT模型考察多维和非理想初值条件下各滤波器性能.GPFF的粒子数量均为100个,步长Δλ=0.05.
5.1平面CWPA模型
平面CPWA模型为目标加速度受随机扰动的连续时间运动模型,以随机微分方程描述如下:


其中,
k=1,2,…,T,T为观测点数,

噪声协方差矩阵

Δt为离散化时间间隔.
以平面位置坐标作为观测量,观测方程为

观测矩阵H=(I2×202×4).设Δt=0.1,T=80.初始状态为x0=06×1,滤波器初始分布为N(x0,P0|0),初始误差矩阵P0|0=diag(0.1,0.1,0.1,0.1,0.5,0.5).分别在高斯噪声和混合高斯噪声条件下进行仿真,即

为直观比较,采用由下式定义的维度无关均方误差(MSE)

图1(a)~(b)分别给出了在不同类型观测噪声下,KF与GPFF的100次MC计算MSE对比.由图可知,在高斯噪声条件下,GPFF与KF误差近似相同,这与2.2中证明的结论是一致的;而在非高斯噪声条件下,KF误差增幅较大,且变得不稳定,而GPFF仍具有较小的误差,这表明GPFF保持了粒子型算法对系统噪声的适应性.
图2给出了非高斯噪声条件下GPFF与KF的跟踪结果对比,可知在非高斯观测噪声下,KF跟踪轨迹与真实轨迹产生了较大偏差,而GPFF仍可准确地跟踪目标.
5.2UNG模型
该模型是非线性滤波中的基准问题[5],其状态空间模型为




图3给出了各个算法 MSE的100次 MC仿真计算结果,其中PF粒子数N=100.由于UNG是一个不含采样时间的完全离散模型,且包含高阶非线性项,导致EKF的一阶线性化误差较大,稳定性较差;GPFF在MSE和稳定性上均显著地优于EKF以及同样采用UT变换的UKF.
表1进一步给出了各个算法100次MC计算的MSE均值和方差以及单次平均计算时间.其中,对于PF 和GPFF分别给出了 N=100,N=500和N=1000时的计算结果(如括号内所示),执行时间在MATLAB R2013(8.1.0.604)版本和2.5GHz双核计算机条件下测得.由表可知,作为高斯型滤波器,GPFF精度优于EKF和UKF;而作为粒子型算法,GPFF的计算量随粒子数量的增长变化是较慢的;PF采用重采样方法,其计算时间随粒子数量增长较快,因此GPFF的计算效率高于PF.综合图表结果看,由于PF对样本分布不基于任何假设,对于本例的情况(一维模型和理想初始条件),其精度最高.而在算例3中将会看到,对于多维问题,PF的性能将会大幅下降.


表1100 次MC计算结果:MSE均值,方差,计算时间
5.3BOT模型
BOT模型[15]是只以方位角测量值作为观测量的跟踪模型,其状态模型为离散Wiener速度模型,


观测噪声vk~N(02×1,R),噪声协方差矩阵R= 0.052I2×2.观测点坐标,设Δt=0.1s,时刻k=1,2,…,T,T= 200.状态初值x0=(0,36,0.2,-1)T,滤波器初始分布为N(^x0,P0|0),初始估计值^x0=(-6,17,0,0)T,初始误差矩阵P0|0=(25,25,1,1)T.PF粒子个数N=500.
采用各算法进行100次Monte-Carlo计算,对于k时刻的某一个状态分量εk,按下式计算各个状态分量的MSE

其中Nm为Monte-Carlo仿真次数,^εk为k时刻状态估计值.由上式可知,MSEkε是100次Monte-Carlo计算的平方误差在特定时刻上的均值,可衡量算法随观测值信息增加的收敛性能.其计算结果如图4(a)~(d)所示,由图可知,EKF、UKF和GPFF均能够收敛到较小的误差范围,而PF则出现了显著偏差,且随时间变化的趋势是起伏的,可见在多维模型和不理想初始值条件下,经典PF的性能较差;进一步地可以看出,相较EKF和 UKF,GPFF能够更快的收敛,且误差较小.
图5(a)~(d)给出了各个算法MSE的100次MC计算结果,可以看到,PF对于目标纵轴坐标的估计产生了很大误差,而对于目标横轴速度估计的MSE则较小,且PF稳定性较差,这种现象是由于y的估计初值与真实初值偏差最大,而.x的估计初值与真实初始偏差很小造成的,这从图4中也可得出.
图4和图5表明一定粒子数量条件下,对于多维估计问题,PF的性能对于初始条件是十分敏感的,若初始条件不够理想的,其平均性能甚至会劣于EKF算法.而GPFF对于每个分量估计的MSE均明显地低于其他算法,具有较高的精度,且在所有仿真中都保持了稳定的性能.
表2中给出了各个算法条件下,100次MC计算所得的状态分量估计MSE均值,方差和执行时间,其中对于PF分别给出了粒子数时的结果.可知各算法中GPFF 的MSE均值为最小,且稳定性好;UKF精度高于 EKF;PF算法在粒子数量为4000时给出了较好的估计结果,但此时其精度仍低于GPFF,表明在不理想初值和/或多维模型条件下,PF若无足够粒子来代表多维样本空间,或建议分布本身就与后验分布相去甚远(不理想的初值),则重采样方法此时是低效的.



表2 MSE均值、标准差和执行时间
6 总结
针对粒子流滤波器中速度场难于计算的问题,基于粒子流滤波器基本理论,导出一种高斯粒子流滤波器.在线性高斯条件下推导了速度场的解析解;证明了当粒子流演化步长趋近于0时速度场解析解与Kalman-Bucy滤波器解的一致性;并将算法推广到非线性系统,利用Unscented变换近似求解.仿真算例表明,算法放宽了系统噪声为高斯型的限制,其精度优于EKF 和UKF等经典非线性高斯滤波器,计算复杂度低于一般粒子滤波器,且性能稳定,具有一定的应用价值.
[1]James C.Bayesian Signals Processing[M].Hoboken:John Wiley&Sons Press,2009.3-10.
[2]Simon J,Jeffery U,Hugh D.A new method for the nonlinear transformation of means and covariance in filters and estimators[J].IEEE Transactions on Auto Control,2000,45(3):477-481.
[3]Arasaratnam I,Haykin S.Cubature Kalman filters[J]. IEEE Transactions on Auto Control,2009,56(6):1254 -1269.
[4]Rudolph M.Sigma-Point Kalman Filters for Probabilistic Inference in Dynamic State-Space Models[D].Oregon:Oregon Health&Science University,2004.251-256.
[5]Gordon N,Salmond D,Smith A.Novel approach to nonlinear/non-Gaussian Bayesian state estimation[J].IEE Radar and Signal Processing,1993,140(2):107-113.
[6]Fred D.Nonlinear filters:Beyond Kalman filter[J].IEEE Aerospace&Electronics Systems Magazine,2005,43(8):57-69.
[7]Synder C,Bengtsson T,Bickel P,et al.Obstacles to highdimensional particle filtering[J].Monthly Weather Review,2008,136(1):4629-4640.
[8]Rudolph M.The Unscented Particle Filter[R].Cambridge:Cambridge University,2000.
[9]Daum F.Coulomb's law particle flow for nonlinear filter[A].Proceedings of SPIE on Signal Processing and Sensor Fusion[C].USA:SPIE Press,2011.3351-3362.
[10]Daum F.Numerical experiments with Coulomb’s law for particle flow in nonlinear filters[A].Proceedings of SPIE Conference[C].San Diego:SPIE Press,2011.2137 -2146.
[11]Fred D,Jim H.Particle flow with non-zero diffusion for nonlinear filters[A].Proceedings of SPIE on Signal Processing and Sensor Fusion[C].USA:SPIE Press,2013. 1745-1755.
[12]Tao D,Mark C.Implementation of the daum-huang exactflow particle filter[A].IEEE Statistical Signal Processing Workshop[C].Ann Arbor:IEEE Press,2012.257-261.
[13]Kotecha J,Djuric P.Gaussian particle filtering[J].IEEE Transactions on Signal Processing,2003,51(10):2592 -2601.
[14]Tao Y,Mehta P G,Meyn S P.Feedback particle filter [J].IEEE Transactions on Automatic Control,2013,58 (10):2037-2043.
[15]Bar-Shalom Y,Xiaorong Li.Estimation with Applications to Tracking and Navigation[M].New York:John Wiley &Sons Press,2005.50-54.
[16]Simon D.Optimal State Estimation[M].New York:John Wiley&Sons Press,2006.22-27.

张宏欣 男,1987年12月出生,陕西汉中人.2010年毕业于西安理工大学,现为海军工程大学博士生,从事统计信号处理及目标跟踪相关研究.
E-mail:mylifeforthebattle@hotmail.com

周穗华 男,1962年10月出生,广东五华人,1984年毕业于海军工程学院,1990年在海军工程学院获得博士学位.现为海军工程大学教授,从事军用目标特性信息处理及武器系统总体设计方面研究.
Gaussian Particle Flow Filter
ZHANG Hong-xin,ZHOU Sui-hua,FENG Shi-min
(Department of Weapon Engineering,Naval University of Engineering,Wuhan,Hubei 430033,China)
Particle flow filter formulated the dynamics from prior samples with posterior samples with particle flow velocity field to perform Bayesian estimation of system state.To address difficulties of particle velocity field computation in present particle flow filter,a novel particle flow filter based on Gaussian assumption was proposed.The analytical solution of velocity field under linear Gaussian condition was derived.The consistency of this analytical solution with Kalman-Bucy filter for continuous system,when discrete dynamic step goes to zero,was proved.The solution was finally extended to obtain the nonlinear Gaussian velocity field expression which can be approximated by using unscented transformation.Several simulations revealed the effectiveness over classic nonlinear Gaussian assumption on accuracy and particle filter on efficiency and stability.
nonlinear filtering;Bayesian estimation;particle flow filter;velocity field;Unscented transformation
TP202
A
0372-2112(2016)04-0795-09
电子学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.04.007
2014-10-28;
2015-03-23;责任编辑:孙瑶

