基于模拟电荷法的微间隙场增强因子研究
钟久明,刘树林,王玉婷,韩长端,刘锦涛
(1.西安科技大学电气与控制工程学院,陕西西安710054;2.海南师范大学物理与电子工程学院,海南海口571158)
基于模拟电荷法的微间隙场增强因子研究
钟久明1,2,刘树林1,王玉婷1,韩长端1,刘锦涛1
(1.西安科技大学电气与控制工程学院,陕西西安710054;2.海南师范大学物理与电子工程学院,海南海口571158)
运动电极下的微间隙是国际电工委员会推荐安全火花试验装置(IEC-STA)短路火花放电体系的核心组成部分,也是研究装置短路放电特性、揭示短路放电机理的关键性难点.为研究其短路放电特性,运用扫描电镜对其电极进行了扫描分析,重构了最危险打火情形下的电极表面形貌模型.基于模拟电荷法建立了阴极表面场强的数学模型,并对传统模拟电荷法进行了改进,给出了其参数设置、算法流程及病态矩阵处理方法,并对场增强因子进行了数值计算.数值计算结果表明,对于给定的微凸起高度,场增强因子与微凸起密度并不成简单的单调关系,而是存在使场增强因子最大的微凸起密度;对于给定的微凸起密度,在电极间距较大的情况下,场增强因子随间距成单调递减关系,反之,则随间距的减小而增大.数值计算结果为IEC-STA短路放电特性研究奠定了基础.
微间隙;IEC安全火花试验装置;短路放电;模拟电荷法;场增强因子
1 引言
IEC(国际电工委员会)安全火花试验装置(IECSTA)是电路本质安全(简称本安)性能测试、评价鉴定的标准设备,研究基于该装置的电容短路放电机理,是进行电路输出本安性能非爆炸评价的前提和基础[1,2].目前,国外关于本质安全电路火花放电及其评价的相关研究鲜有报道,而国内关于本质安全电路的相关研究大多集中在本质安全电路设计及实验评价等工程应用领域.关于本质安全电路放电机理方面,国内学者的研究大多集中在电感断路放电及内部本安性能评价等领域,而针对IEC安全火花试验装置电容短路放电机理的研究未见相关报道[1~4].
运用IEC-STA进行相关试验时,由于电极放电相对面存在微米量级的金属微凸起,且微凸起的几何尺寸与短路放电的临界击穿间距相比显然不能忽略,因此研究阴极表面微凸起与极间场强的定量关系,成为场增强因子及场致发射电流计算所必须解决的首要问题及关键性难题[5,6].
文献[7,8]运用数值方法对金属微凸起电场增强因子进行研究,但是其理论模型仅适用于电极间距远大于微凸起高度的电极系统,且未考虑微凸起密度对场增强因子的影响.
分析场发射器件(如碳纳米管)的场发射性能时,场增强因子的分析和计算极为重要[9,10],但与此相关的研究只适用于碳纳米管阵列这一类可忽略边界效应的物理结构及物理模型,而对IEC-STA而言,当电极间距足够小时,微凸起高度显然无法忽略,因此,探索行之有效的数值算法十分必要.
模拟电荷法具有原理简单、无需封边、误差小,无需通过梯度求场强的优点.而且它还具有计算公式和程序简单、不存在奇点处理问题以及电极表面附近的场强计算精度高的特点.因此,本文在电极微观表面分析的基础上,运用模拟电荷法计算不同电极间距下的阴极表面场强及场增强因子,为电容短路放电的分析及本安电路的非爆炸评价奠定理论基础.
2 电极系统微观表面形貌分析
IEC-STA的短路放电试验基本过程为:密闭的容器内充满特定的气体介质,其中布置一对钨丝和镉盘电极,钨丝以 v≈0.25m/s的速率向旋转镉盘电极靠近直至短路[1,2].
由于IEC-STA短路放电过程中,电极的短路接触点是随机的,因此,不可能运用重构的方法建立一个既反映电极表面全局特征也反映电极表面的微观局部特征的三维表面形貌模型[11,12].
事实上,建立统一的电极微观表面模型亦无必要;其原因在于运用IEC-STA进行短路放电试验的目的是寻找短路打火最危险的情况,产生最苛刻的检验条件,并在此条件下评价电路是否本安.有鉴于此,建立IECSTA电极三维表面形貌模型时可以产生最危险打火能量的接触点形貌为约束,并通过适当的放大处理,建立电极表面形貌模型.为获取电极表面微观特征并建立表面形貌模型,运用扫描电镜(SEM)分别对钨丝与镉盘在放电相对面的微观表面形貌特征进行实验测试,测试结果表明钨丝侧边的微观表面比较光滑,无明显的表面微凸起,而镉盘的微观表面存在不规则分布的微米量级凸起.
在不考虑表面微附加物等对电极表面发生性能影响的情况下,对于规则且均匀分布的微凸起,其长径比越大,场增强因子通常越大,相同的宏观场强下获得发射电流就越大,其短路放电能量也越大[13,14],该情形下的短路放电就越危险.因此,以最危险短路打火方式为目标约束进行适当的放大处理:假设钨丝电极表面绝对光滑,而镉盘电极表面存在规则且均匀分布的圆柱形微凸起,且以凸起最高、顶端半径最小作为圆柱形凸起的统一高度和半径,并以凸起密度为变量,通过数值求解获得使场增强因子最大的密度分布,以最危险打火方式为目标,取最危险的放电截面建立以凸起高度、半径、密度参量为表征的二维微观表面模型,如图1所示.
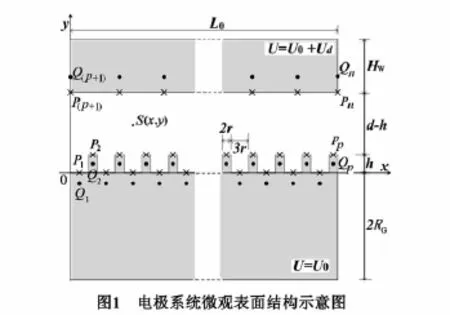
在图1中,2RG=30mm为镉盘的直径,h和r分别为镉盘表面微凸起的高度和半径,Hw=0.2mm为钨丝电极的直径,L0=1mm为钨丝与镉盘相交部分的长度,d为电极间距.
研究场增强因子与电极微观表面特征参量之间的数值关系,关键在于极间电场计算.下面运用模拟电荷法计算不同间距下的电极表面电场及其场增强因子.
3 基于CSM的电场强度计算
根据CSM基本原理,场域内任意点的电位与场强可由各模拟电荷所产生的场量叠加而获得,从而获得原场的近似解.下面给出具体的算法步骤.
3.1匹配点的设置
匹配点太密则计算量加大,并使方程的条件数变坏,易使系数矩阵产生病态;太少则无法全面描述边界特征,计算精度低、误差大.因此,根据图1所示的电极微观表面结构示意图,在镉电极表面的每一个凸起与凹槽处各布置一个匹配点,用“×”标记,其编号顺序如图1所示.
3.2模拟电荷的布置
根据电极表面形貌特征,模拟电荷类型取点电荷.设置模拟电荷数量与匹配点数量相等.模拟电荷正对匹配点,并布置在边界的垂直线上.设模拟电荷相对边界面的垂直距离为a,该处左右相邻两匹配点间的距离为b,取两者的比值f=a/b.f一般为0.2~1.5,通常可取0.75,当匹配点分布疏时,f取较小值,反之取较大值[15].由于阴极和阳极表面匹配点的疏密程度不一样,比例系数也不一样,设阴极内部的比例系数为 f1,阳极内部的比例系数为f2.模拟电荷用“·”标记,其编号如图1所示.
3.3模拟电荷量值的确定
由于该电极系统为孤立的带电系统,若以阴极或阳极上的任意点为参考点,则运用模拟电荷法求解时,参考点的电位方程无法确定.因此,以无穷远处为电位参考点,并假设阴极电位(镉盘电极)的电位为U0,则阳极(钨丝电极)电位为U0+Ud,其中Ud为阳极与阴极之间的电位差.
根据叠加原理,对于阴极上的匹配点,由设定的模拟电荷所建立的电位方程为
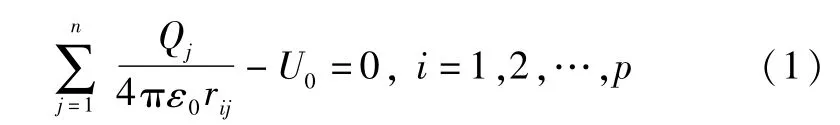
其中,Qj是第j个模拟电荷的电荷量,n为模拟电荷总个数,i=1,2,…,p依次表示阴极上的各匹配点,p为阴极上的匹配点总数.为第j个模拟电荷到第i个匹配点的距离,表示第j个模拟电荷对第i个匹配点电位的贡献,称为电位系数.
同理,对于阳极上的匹配点,由设定的模拟电荷所建立的电位方程为
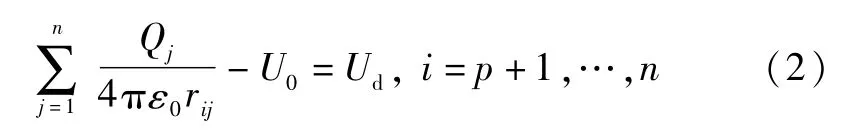
其中,i=p+1,…,n依次表示表示阳极上的各匹配点,n为匹配点总数.
根据电荷守恒定律,可补充方程

综合式(1)、(2)和(3),并考虑到方程式中的电位系数rij和电极间距d均为微米量级,为计算方便,将方程式进行恒等变换:电位系数中的坐标单位选为微米,而待求的模拟电荷量由库伦转换为单位电荷个数,代入普适物理常量:1e=1.6×10-19C,ε0=8.85×10-12Fm-1,整理后可得

式(4)共有n+1个代数方程,第1个为电荷守恒方程,第2~p+1和p+2~n+1个分别为阴极上和阳极上匹配点的电位方程,待求的未知数有Q1,Q2,…,Qn以及U0共n+1个.
由于系数矩阵A的条件数往往很大,方程组(4)多为病态方程组,系数矩阵的微小扰动将引起解的巨大变化,从而使数值计算不稳定.为此,本文采用一种简单实用的迭代算法处理该病态问题.
3.4模拟电荷的校验
为检验模拟电荷设置的合理性,需对解得的模拟电荷量值进行校验.
在阴极和阳极表面上,在匹配点旁边选取相同数量的校验点,重新计算电位系数,代入式(4),得各校验点的电位计算值,若计算值与已知值误差足够小,电极表面自由电荷的作用可由设置的该组模拟电荷等值替代.若误差不满足要求,则调整模拟电荷设置(位置、数量和形态),直至满足计算精度要求为止.
3.5电场计算
假设S为场域内的任意一点,其坐标为(x,y),如图1所示.
根据叠加原理,任意一点的电场强度可由所有模拟电荷在该点所形成的场强叠加而得,即
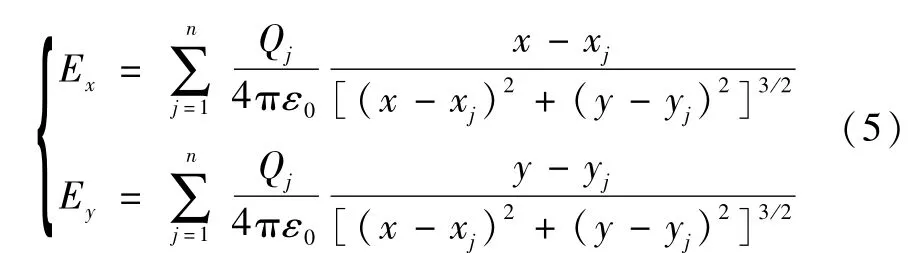
其中Ex、Ey分别为场强E在x和y方向上的分量,(xj,yj)为第j个模拟电荷的位置坐标.由于场致发射电流仅与其y方向的场强有关,所以,事实上仅需计算其y方向的场强分量.
4 场增强因子计算
根据第2节理论分析,对于给定极间电压、极间距以及阴极表面微凸起参量的电极系统,运用上述模拟电荷法可求得每一个微凸起尖端处的场强,取其平均值与宏观场强之比,可得给定参数下的场增强因子.
然而,运用传统模拟电荷法进行电场强度数值计算的过程中,模拟电荷的数量及其位置等关键参量的设置均由设计者凭经验给出,因此,需要对传统的模拟电荷法进行优化和改进[15],下面结合本课题所面对的工程问题给出一种简单实用的优化算法.
对传统模拟电荷法进行优化之前,首先根据电极表面形貌设定匹配点数目及其位置,然后令模拟电荷数等于匹配点数,接下来重点对模拟电荷的位置进行优化配置.优化算法步骤如下:
(1)按传统方法设置匹配点数目及其位置;令模拟电荷数等于匹配点数,并使模拟电荷在过匹配点的边界垂直线上分布.
(2)以0.1为步长将f1和f2分成若干等份,取 f1和f2为初值0.1.
(3)按传统方法计算模拟电荷量及校验点的平均误差.
(4)变换f1和f2的取值,重复第3步的计算,直至f1和f2的取值超出设定的范围.
(5)取平均误差最小时所对应的f1和f2取值,为f1和f2的最优解.
(6)计算f1和f2为最优值,即平均误差最小时的阴极表面场强等参量.
5 计算结果及分析
设极间电位差为24V、极间距为25μm.取镉盘表面微凸起参量为:高度h=5μm、半径r=0.5μm,间隔5r.在阴极表面每一个凸起和凹陷中心处各设置一个匹配点,则在钨丝与镉盘相交部分长度1mm范围内设置571个匹配点.将阳极表面分为200等份,在每一个等份点及边界点各设置一个匹配点,即阳极表面设置201个匹配点,在电极内部、与匹配点垂直相对位置依次设置772个模拟电荷.
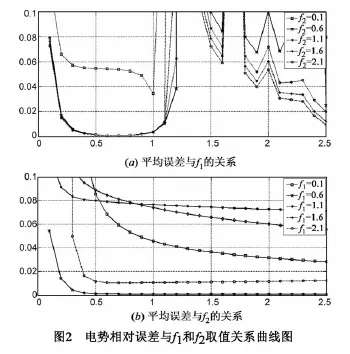
分别取f2=0.1、0.6、1.1、1.6、2.1,依次画出平均误差与比例系数 f1的关系曲线,如图2(a)所示.从图2 (a)可看出,固定f2,平均误差与f1成复杂的非线性关系.类似地,分别取f1=0.1、0.6、1.1、1.6、2.1,依次画出平均误差与比例系数f2的关系曲线,如图2(b)所示.不难看出,f1取值不变时,随着 f2的增大,平均误差先增后减.综合图2(a)、图2(b)可知,当f1=0.6、f2=2.5时,电极表面校验点电势平均相对误差最小.
可见,模拟电荷在电极表面的合成电位等势面与电极表面形状高度逼近,因此,电极表面自由电荷在空间激发的电场可由该组设定的模拟电荷等值替代.根据场叠加原理及式(5),可求得各微凸起尖端中心处场强的平均值约为1.37×106V/m,而宏观场强E0=Ud/d =24/(200×10-6)=012×106V/m,即当极间距为200μm时,由微凸起引起的场增强因子为β1=1.37/ 0.12=11.42.
将给定参数代入具有类似物理模型的文献[9]所得公式,可得场增强因子为12.3,与本文计算结果极为接近.
为考察微凸起密度对场增强因子的影响,固定电极间距d=200μm、微凸起高度h以及半径r,取不同的微凸起密度,本文数值计算结果与文献[9]的对比如图3所示.

可见,采用CSM的数值计算结果与文献[9]的解析计算结果吻合良好,两者均表明场增强因子与微凸起密度并不成简单的单调关系,当凹槽宽与凸起半径之比约为5时,场增强因子最大,对应的微凸起密度约为8.18×104/mm2.其原因在于:当微凸起密度较小时,临近微凸起表面电荷间的库仑力作用力较小,使得微凸起上的电荷无法在尖端处充分集中,而使场增强因子下降;当微凸起密度较大时,凸起尖端之间的屏蔽作用加强,从而削弱了凸起尖端处的场强,而使场增强因子下降,这与文献[8]的实验分析亦相符合.
以上计算结果及对比分析表明,模拟电荷法用于IEC-STA电极系统的场增强因子计算时结果可信、方法有效.
IEC-STA短路放电过程中,放电的临界击穿间距较小,一般为几十微米,而且极间距逐渐缩小直至短路,短路放电过程中微凸起高度与极间距相比显然无法忽略不计,文献[8,9]等解析算法所基于的物理模型已失效,所以,考察极间距对场增强因子的影响只能用数值算法.
设阴极表面微凸起高度h=5、半径r=0.5及凹槽宽为5r(对应的微凸起密度为时阴极表面场强最强的密度),取0.1≤f1、f2≤2.5,运用图4所示算法流程计算不同极间距下的场增强因子,仿真计算结果表明,当f1=0.6、f2=2.5时校验点的平均误差最小,最小值为3.6 ×10-4.取f1=0.6、f2=2.5可得场增强因子与极间距的关系如图4所示.

从图4的数值计算结果可看出,场增强因子与极间距之间并不成简单的单调关系,随着间距的减小,场增强因子先减小后增大,存在一个最小的场增强因子.运用数值拟合的方法可获得该情形下场增强因子与极间距的数值关系近似为:β=5.08×10-5d3+8.80×10-3d2-0.334d+8.15,其中d的单位为μm.究其原因在于:一方面,在极间电压不变的情况下,随着间距的减小,极间宏观场强增大而使场增强因子减小;另一方面,随着间距的减小,阳极逐渐靠近阴极,阳极与阴极微凸起上电荷之间的库仑力加强,尖端处电荷密度增大,使阴极微凸起尖端的微观场强增大从而使场增强因子增大.当间距较大时,库仑力作用不明显,前者占主导地位,表现为场增强因子随间距的减小而减小;当间距较小时,库仑力作用明显,后者起主导作用,所以表现为场增强因子随间距的减小而增大.
6 结论
本文首次将模拟电荷法应用于IEC-STA短路放电过程中阴极表面微观场强分析及其场增强因子的计算,得到的主要结论有:
(1)考虑到表面微凸起的作用,开放边界的微间隙电极系统的电场强度数值计算可用模拟电荷法实现.
(2)IEC-STA短路放电过程中,给定微凸起高度和半径情形下,场增强因子与微凸起密度并不成简单的单调关系,当微凸起密度约为8.18×104/mm2时场增强因子最大.
(3)取使场增强因子最大时的微凸起密度、半径和高度,当间距较大时,场增强因子随间距呈单调递减关系,反之,场增强因子随间距的减小而增大.该情形下,场增强因子β与极间距d的数值关系近似为β=5.08 ×10-5d3+8.80×10-3d2-0.334d+8.15.
本文针对开放性的复杂边界动态电极系统极间场强的数值计算,进行了有益的探索,并对传统的模拟电荷法进行了改进,提出了优化算法,减小了计算量,为该类问题提出了一种有效的解决方法.
[1]刘树林,崔强,李勇.Buck变换器的输出短路火花放电能量及输出本质安全判据[J].物理学报,2013,62(16):148601-1-148601-10. LIU Shu-lin,CUI Qiang,LI Yong.Output short-circuit spark discharging energy and output intrinsic safety criterion of Buck converters[J].Acta Physica Sinica,2013,62(16):148601-1-148601-10.(in Chinese)
[2]刘树林,刘健,钟久明.buck-boost变换器的能量传输模式与输出纹波电压分析[J].电子学报,2007,35(5):838 -843. LIU Shu-lin,LIU Jian,ZHONG Jiu-ming.Energy transmission mode and output ripple voltage of Buck-Boost converters[J].Acta Electronica Sinica,2007,35(5):838-843. (in Chinese)
[3]刘树林,钟久明,樊文斌,等.电容电路短路火花放电特性及其建模研究[J].煤炭学报,2012,(12):174-179. LIU Shu-lin,ZHONG Jiu-ming,FAN Wen-bin,et al.Short circuit discharge behavior of the capacitive circuit and its mathematical model[J].Journal of China Coal Society,2012,(12):174-179.(in Chinese)
[4]钟久明,刘树林,崔强.IEC火花试验装置的电容短路放电特性数学仿真分析[J].电工电能新技术,2014,33 (2):29-34. ZHONG Jiu-ming,LIU Shu-lin,CUI Qiang.Short circuit discharge behavior of capacitive circuit and its mathematical simulation analysis[J].Advanced Technology of Electrical Engineering and Energy,2014,33(2):29-34.(in Chinese)
[5]G N Fursey.Field emission and vacuum breakdown[J]. IEEE Transactions on Electrical Insulation,1985,EI-20 (4):659-670.
[6]Y Hirata,K Ozaki,U Ikeda,M Mizoshiri.Field emission current and vacuum breakdown by a pointed cathode[J]. Thin Solid Films,2007,515(9):4247-4250.
[7]Kokkorakis G C,Modinos A,Xanthakis J P.Local electric field at the emitting surface of a carbon nanotube[J].Journal of Applied Physics,2002,91(7):4580-4584.
[8]Edgcombe C J,Valdr U.The enhancement factor and the characterization of am orphous carbon field emitters[J]. Solid State Electron,2001,45(6):857-863.
[9]朱亚波,王万录,廖克俊.对碳纳米管阵列的场发射电场增强因子以及最佳阵列密度的研究[J].物理学报,2002,51(10):2335-2339. ZHU Ya-bo,WANG Wan-lu,LIAO Ke-jun.Study on the electric field enhancement factor and the optimum densities of carbon nanotube arrays[J].Acta Physica Sinica,2002,51(10):2335-2339.(in Chinese)
[10]Zarko D,Ban D,Lipo T A.Analytical calculation of magnetic field distribution in the slotted air gap of a surface permanent-magnet motor using complex relative air-gap permeance[J].IEEE Transactions on Magnetics,2006,42 (7):1828-1837.
[11]Reizer R.Simulation of 3D Gaussian surface topography [J].Wear,2011,271(3-4):539-543.
[12]Wang Z Y,Meng H,Fu J H.Novel method for evaluating surface roughness by grey dynamic filtering[J].Measurement,2010,43(1):78-82.
[13]刘蜀阳,韩志宏,吴南星,等.负极性电火花加工时表面做功能量研究及其参数分析[J].电子学报,2014,42(3):578-582. LIU Shu-yang,HAN Zhi-hong,WU Nan-xing,et al.The study of work energy on machined surface during negative polarity EDM and its parameters analysis[J].Acta Electronica Sinica,2014,42(3):578-582.(in Chinese)
[14]刘蜀阳,黄玉美.负极性电火花加工时的电极损耗机理及积碳层的减损作用研究[J].电子学报,2012,40(4):654-660. LIU Shu-yang,HUANG Yu-mei.The study on the wear mechanism ofelectrodematerialsinnegativeEDM process and the effect of carbon deposition layer[J].Acta Electronica Sinica,2012,40(4):654-660.(in Chinese)
[15]袁述,袁东辉,孙基周,等.蚁群-遗传算法在多传感器多目标跟踪技术中的应用[J].电子学报,2013,41(3):609-614. YUAN Shu,YUAN Dong-hui,SUN Ji-zhou,et al.The application of AG-GA on multi-sensor multi-target tracking [J].Acta Electronica Sinica,2013,41(3):609-614.(in Chinese)

钟久明 男,1975年8月出生于江西宁都,博士,研究领域为本质安全开关变换器、气体放电.
E-mail:jiumingxyz@163.com

刘树林(通讯作者) 男,1964年12月出生于四川成都,博士、教授、博士生导师.研究领域为开关变换器、功率集成电路.发表论文100余篇,其中SCI、EI收录60余篇次;出版专著及教材6部,其中国家“十一五”规划教材1部.
E-mail:lsigma@163.com
Study on the Electric Field Enhancement Factor for Micro-Gap Based on CSM
ZHONG Jiu-ming1,2,LIU Shu-lin1,WANG Yu-ting1,HAN Chang-duan1,LIU Jin-tao1
(1.School of Electrical and Control Engineering,Xi’an University of Science&Technology,Xi’an,Shaanxi 710054,China;2.School of Physic and Electronics Engineering,Hainan Normal University,Haikou,Hainan 571158,China)
The moving electrode micro-gap is a core part of short-circuit spark discharge system of safety spark test apparatus(STA)specified by the international electrotechnical commission(IEC),it is the key difficulty of researching on IEC-STA short circuit discharge mechanism and characteristic.In order to establish the mathematical models of capacitive circuit short-circuit discharge on the IEC-STA,its electrodes are scanned with scanning electron microscope(SEM).A physical model of the electrodes micro surface in the most dangerous case is established.Mathematical models of IEC-STA cathode surface electric field are established by improved charge simulation method(CSM),the parameters setting,algorithm technological process and the method for ill-conditioned matrix are presented.The numerical computation for IEC-STA cathode surface electric field in different micro-protrude density being developed with CSM shows that there is one density which makes the electric field enhancement factor be the highest.The cathode surface electric field in different electrodespacing being calculated with CSM shows that the enhancement factor decreases with the reduced electrode-spacing when the electrode-spacing is longer,while it increases with the reduced electrode-spacing when it is shorter.The results will prepare for the further research on the short-circuit discharge with IEC-STA.
micro-gap;IEC safety spark test apparatus;short-circuit discharge;charge simulation method;electric field enhancement factor
O462
A
0372-2112(2016)04-1003-06
电子学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.04.035
2014-10-13;
2015-07-17;责任编辑:孙瑶
国家自然科学基金(No.50977077,No.51277149)

