基于稀疏相似保持算法的人脸识别

冯海亮，王应健，罗甫林



基于稀疏相似保持算法的人脸识别

冯海亮，王应健，罗甫林

( 重庆大学 光电技术及系统教育部重点实验室，重庆 400044 )

鉴于人为选取近邻大小和权重矩阵对局部保持投影(LPP)算法的高维人脸图像特征提取有较大影响，结合稀疏表示原理提出了一种稀疏相似保持(SSP)算法。SSP算法利用稀疏表示，在全局结构中自适应地选取数据间的相似关系，构建非负稀疏关系图，在低维空间中保持高维原始数据的内在稀疏特性不变，能有效地提取出低维鉴别特征。在Extend Yale B、CMU PIE人脸数据库上进行实验，其识别率分别达到了87.35%、90.09%，验证了算法的有效性。

人脸识别；局部保持投影；稀疏图；稀疏相似保持

0 引 言

人脸识别是模式识别领域的一个重要研究项目，在人工智能、公共安全等领域具有巨大的应用前景。由于人脸图像是典型的高维数据，为避免“维数灾难”，人们提出了各种各样的维数约简方法。传统的降维方法，如主成分分析(Principal Component Analysis，PCA)[1]、线性判别分析(Linear Discriminant Analysis，LDA)[2]是全局线性降维方法，而研究表明，人脸空间更可能存在于非线性流形子空间中。为此，研究人员提出了一系列基于流形的子空间学习方法，如等距映射(Isometric Mapping，ISOMAP)[3]、局部保持嵌入(Locally Linear Embedding，LLE)[4]和拉普拉斯特征映射(Laplacian Eigenmaps，LE)[5]。该类方法的主要思想是假设每个样本数据点和其邻域点位于一个线性或近似线性的流形上，采用非线性映射方式，在低维嵌入空间中保持数据间的内在结构关系不变。通过流形学习方法学习样本数据就能有效地揭示数据中的内在属性，进而得到隐含鉴别特征。但是这些方法只在所学习的样本中有定义，对外来的新样本无法直接进行投影，使其泛化能力受到限制。为此，He等人提出LE和LLE的线性近似方法，分别为局部保持投影(locality Preserving Projection，LPP)[6]和邻域保持嵌入(Neighborhood Preserving Embedding，NPE)[7]。其中LPP通过投影矩阵把LE中隐含的非线性映射转换为线性映射，因而能够直接通过投影矩阵得到新样本数据点在嵌入空间中的映射。虽然LPP本质上为线性方法，但同传统的主成分分析(PCA)、线性判别分析(LDA)等方法相比，LPP算法能够在嵌入空间中保持数据原始空间的局部几何结构，进而揭示出高维空间中的内在低维流形结构。在LPP 算法中需要通过欧氏距离选取近邻，但是欧氏距离受数据噪声影响较大，且人为设置的近邻大小不能自适应地反映局部结构特性，导致所提取的特征鉴别力不足[8]。

作为近年来新兴的一种数据表示方法，稀疏表示以其良好的鲁棒性、抗干扰能力、可解释性和判别性等优势，在人脸识别领域引起了广泛关注。Qiao[9]等提出了稀疏保持投影(Sparsity Preserving Projection，SPP) 的人脸识别算法，较好的反映了人脸图像全局非几何结构，然而SPP算法没能得到子空间的正交向量基，这使其真实表征数据变得困难；Liu[10]等提出了一种稀疏保持嵌入(Sparsity Preserving Embedding with Manifold Learning and Discriminant Analysis，SPE)算法，以鉴别分析和流形学习为基础，利用稀疏表示理论，在低维嵌入空间中保持数据在高维空间中的稀疏特性不变，即通过非负稀疏表示揭示出各类型数据在高维空间中的内在特性。然而，包括 SPP 和SPE 在内的基于稀疏表示的人脸识别方法，在对原始样本进行稀疏重构时都没有很好的利用样本之间的局部结构信息，极易造成误学习。

结合LPP和稀疏表示各自的优点，本文提出了一种稀疏相似保持(Sparse Similarity Preserving，SSP)算法。SSP算法根据稀疏表示揭示出高维数据在全局结构中的相似关系，并通过非负稀疏系数大小来反映相似性程度，构造非负稀疏关系图，在低维嵌入空间中保持数据在高维空间中的稀疏特性不变，受局部结构关系的影响小，能有效地提取出低维鉴别特征。SSP算法根据稀疏表示原理自动地选取数据间的相似关系，减小了近邻设置和选取方式带来的影响。选取Extend Yale B人脸数据库和CMU PIE人脸数据库进行识别率实验和算法的有效性验证。

1 相关原理分析

1.1 局部保持投影算法(LLP)

局部保持投影算法(LLP)是通过数据集构建反映数据流形结构的无向权重图矩阵={，}，其中为图中的顶点，表示各顶点对应边的权值矩阵。LLP的特点是用一个保持顶点间相似关系不变的低维向量来表征图的每个顶点，用边的权值衡量顶点间的相似性。

LPP算法的主要步骤为

1) 构造近邻关系图。采用近邻法得到近邻，若x与x为近邻，则在近邻关系矩阵中有边连接；否则无边连接。

3) 计算投影矩阵。投影矩阵可以通过求解如下目标函数最小化问题得到：

1.2 稀疏表示

近年来，信号的稀疏表示在模式识别等相关领域已引起研究人员极大的兴趣。稀疏表示的主要思想是利用字典，将信号表示成少数原子的线性组合，以一种简洁、稀疏的形式反映信号的主要特征和内在结构。

过完备字典是指样本维数小于样本个数(即>)。稀疏表示是对通过中的少数几个能够反映内在特征的元素来近似表示，它是一个全局性的算法。其求解模型为

2 稀疏相似保持算法

由稀疏表示理论可知，稀疏表示能够较好的揭示各数据在全局结构的内在特性，具有自然鉴别能力和自动选择近邻功能。由LLP算法理论可知，LLP能够在低维空间很好的保持高维空间中原始数据顶点间相似关系不变，具有良好的维数约简效果，但是人为选取近邻大小和权重矩阵对LLP的结果有较大影响。针对这种情况，本文提出了一种稀疏相似保持(Sparse Similarity Preserving, SSP)算法。SSP算法在全局结构中自适应地选取数据间的相似关系，构造非负稀疏关系图，能够在低维空间中保持高维空间中原始数据的稀疏特性不变。因此，它在构建无向权重图时不需要任何模型参数，并且保留了数据的稀疏结构关系。

SSP算法首先使用稀疏表示计算图的相似矩阵。式(3)是一个NP-hard问题，可以把求解范数最小化问题转换为求解范数最小化问题。为得到非负稀疏系数，增加约束条件。因此，我们采用非负稀疏表示得到非负稀疏系数矩阵。其稀疏求解函数变为

然后根据非负稀疏系数矩阵构建无向图，在图中，如果两顶点与之间的非负稀疏系数为非零，就在这两个顶点间设置一条边，相应的权值设为该两点间的非负系数，即；如果两顶点与之间非负稀疏系数为零，该两个顶点之间不设置边，相应的权值为0，即。为在低维嵌入空间保持稀疏特性，目标函数设置如下

其中：tr(×)表示矩阵的迹，为对角矩阵，且；为拉普拉斯矩阵，且；为权值矩阵，即。为得稳定解，使降维数据对矩阵单位化，增加约束：

则目标函数可被转换成如下最小化问题：

对式(7)用Lagrange乘子法可得：

通过对式(8)求取广义特征值特征向量，取出个最小的特征值及其对应的特征向量，令，则降维数据为。

3 实验结果与分析

为验证算法的有效性，本文分别选取Extend Yale B人脸数据库和CMU PIE人脸数据库进行实验。实验中，将所有的人脸图像基于眼部对齐裁剪为32 pixels×32 pixels大小，并将人脸图像归一化处理。实验选取最近邻分类器(Nearest Neighbor, NN)估算识别率。为研究算法的特征提取效果，对PCA、NPE、LPP、SPP、MFA(Marginal Fisher Analysis)[11]、DLSP(Discriminative Learning by Sparse Representation Projections)[12]、SSP进行了不同训练样本下总体识别率随嵌入维数变化的对比实验。所有训练图片均采用随机抽取的方法获得，并重复进行10组实验，最后取10次实验结果的均值作为最终结果进行分析。

3.1 Extend Yale B人脸数据库实验

Extended Yale B人脸库包含有38个人，每人有约64张不同光照条件下的近似正面人脸图像，共计2 414幅人脸图像。图1展示了Extended Yale B人脸库部分人脸样本图像，体现出了明显的光照、表情变化以及轻微的姿态变化。在实验中，从该库中的38类样本随机选取每类中的个样本组成训练集，剩余个样本组成测试集。

图1 Extended Yale B人脸库中某一个人的部分人脸图像

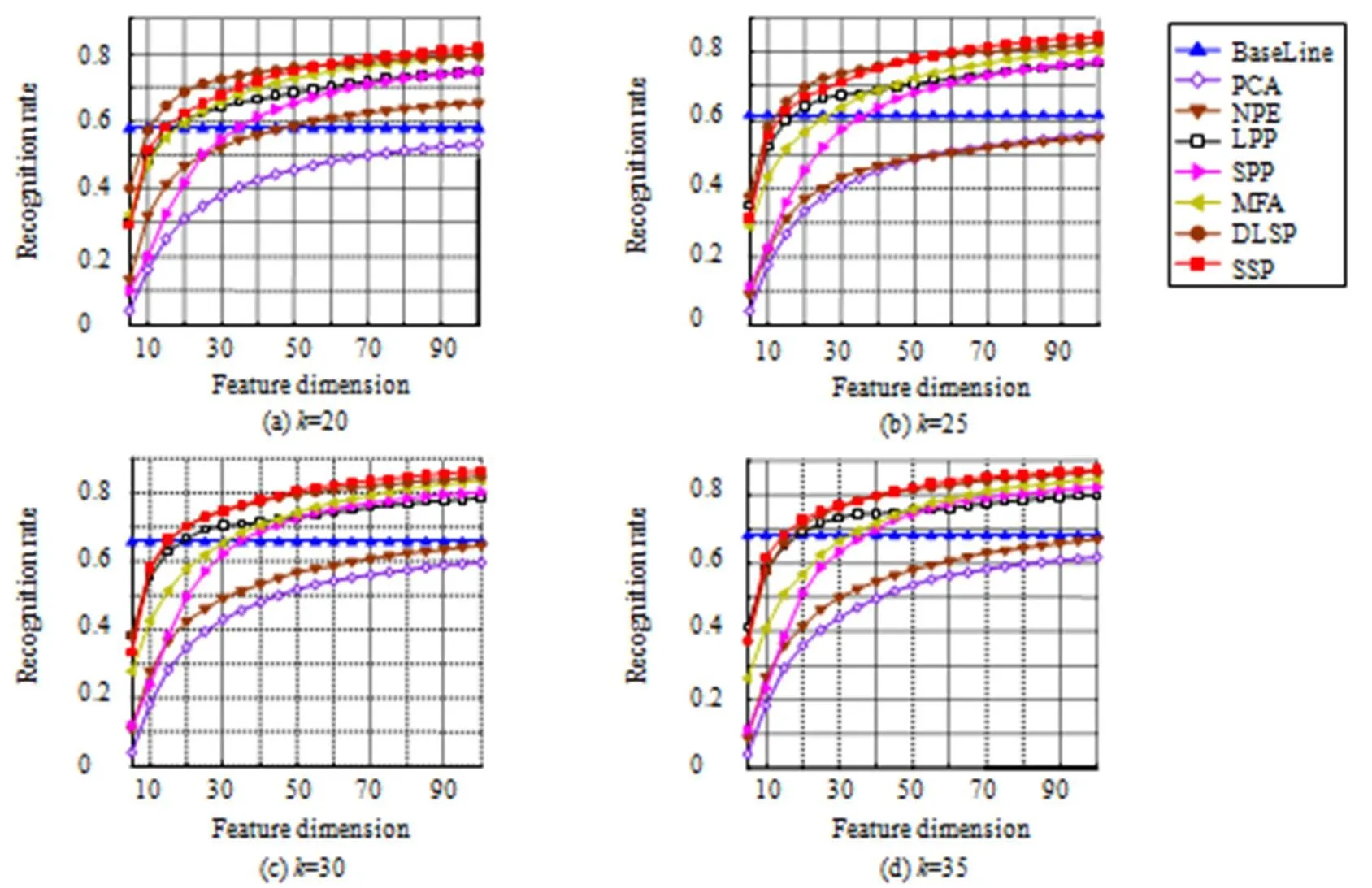
图2 Extend Yale B人脸库中各算法在不同训练样本数不同维度下的总体识别率

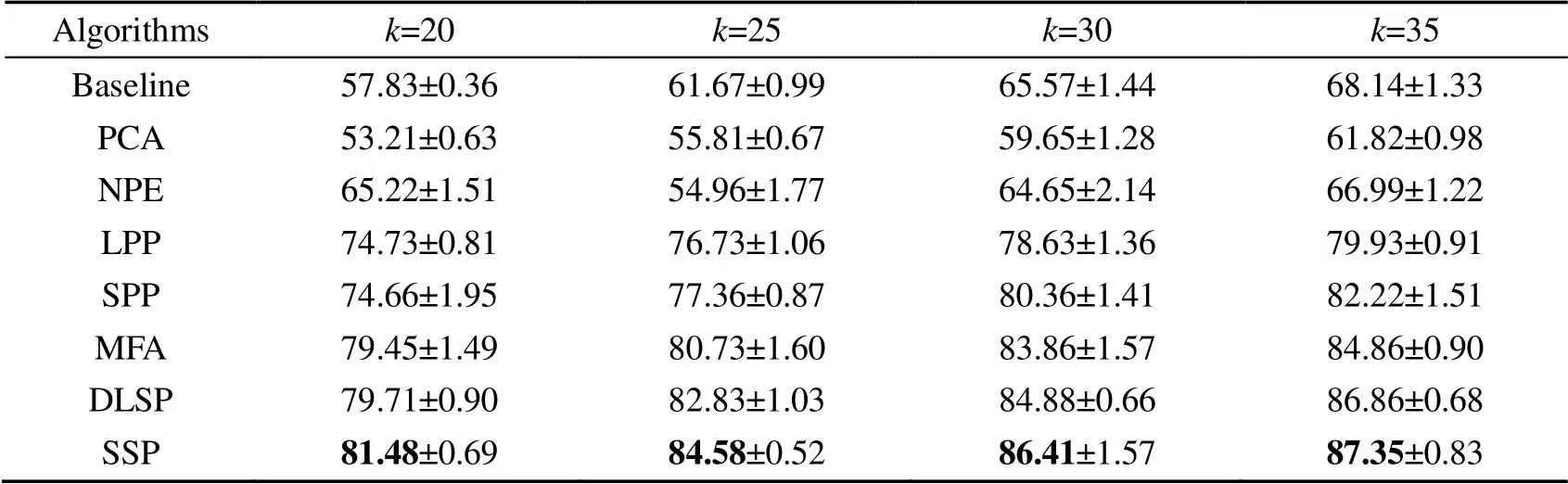
表1 Extend Yale B人脸库中各算法总体识别率的最高值及其方差(平均值±方差)

由图2和表1可知，随着训练样本数的增加，各算法的总体识别率和最高总体识别率都呈现出增加趋势，这是因为训练样本数越多，已知信息越丰富，在特征提取时，可利用的信息就越充足，使各算法的总体识别精度也就越高。显然，SSP算法比PCA、NPE、LPP、SPP、MFA、DLSP的总体识别率和最高总体识别率都好，这是因为SSP算法通过稀疏表示能够很好地从全局结构中揭示出数据间的相似关系，减小了局部几何结构带来的影响，且不受近邻选取和选取方式的影响，并能较好地体现出各类型数据在全局结构中的相似关系，降维后保持相似关系不变，使提取出的鉴别特征更有效，总体识别精度更好。

3.2 CMU PIE人脸数据库进行实验

PIE人脸库含有68个人，每个人13种姿态，43种光照条件，4种表情，共41 368张图片。本文选择在所有光照条件和表情条件下的5个近似正向的姿态(C05，C07，C09，C27，C29)，每个人170张，总共11 560张图片。图3展示了PIE人脸库中某一个人的部分人脸图像，体现出了明显的光照、表情变化以及轻微的姿态变化。

图3 PIE人脸库中某一个人的部分人脸图像

在实验中，从该库中的68类样本随机选取每类中的个样本组成训练集，剩余个样本组成测试集。图4给出了各种算法总体识别率随训练样本数和维数变化的结果，表2给出了在不同训练样本下不同算法总体识别率的最高值及其方差。由图4和表2可知，本文提出的SSP算法的识别率是最好的，SSP算法在全局结构中自适应地选取数据间的相似关系，构造非负稀疏关系图，能够在低维空间中保持高维空间中原始数据的稀疏特性不变，增强了算法的识别性能，因此能够获得最好的识别性能。

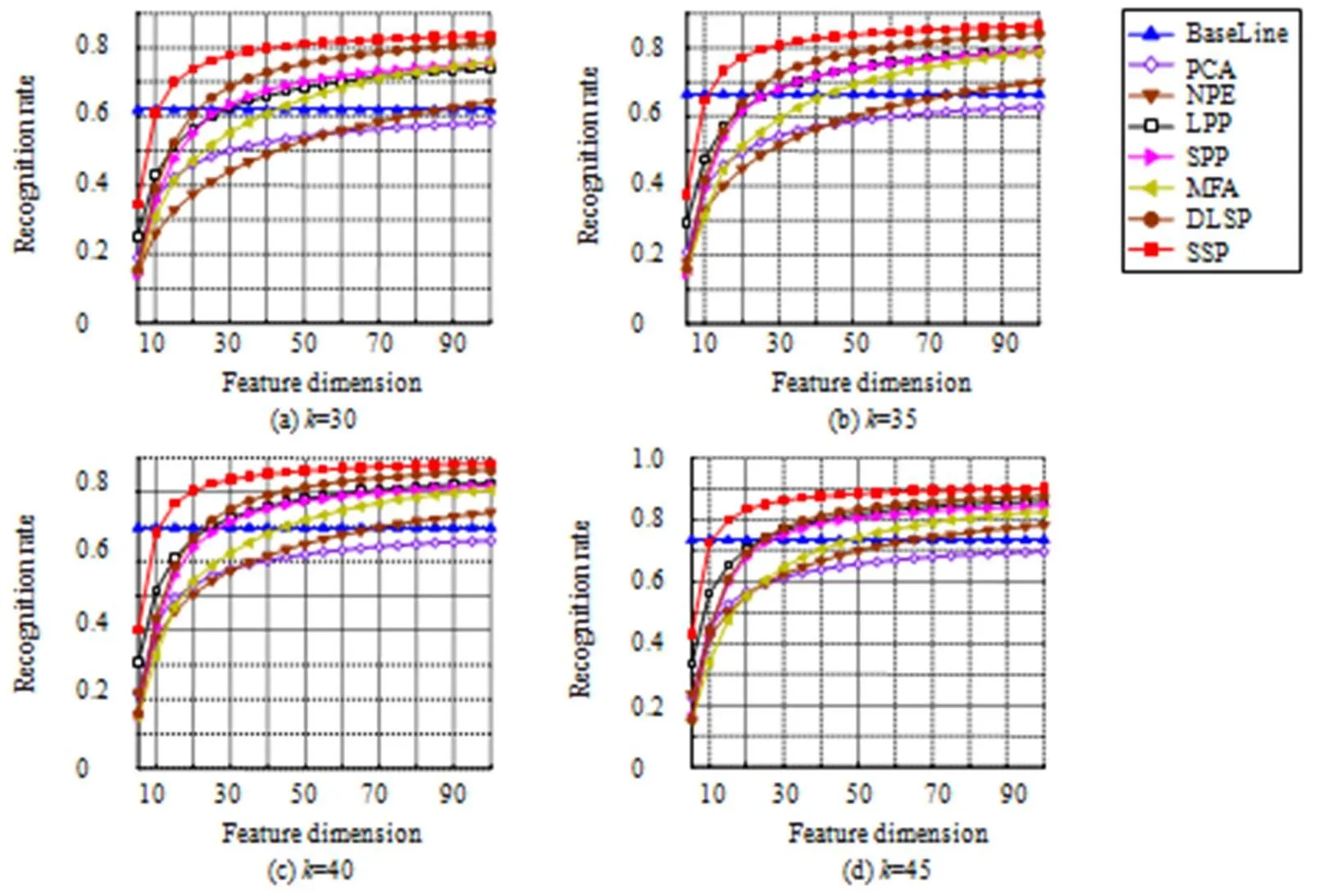
图4 CMU PIE人脸库中各算法在不同训练样本数不同维度下的总体识别率

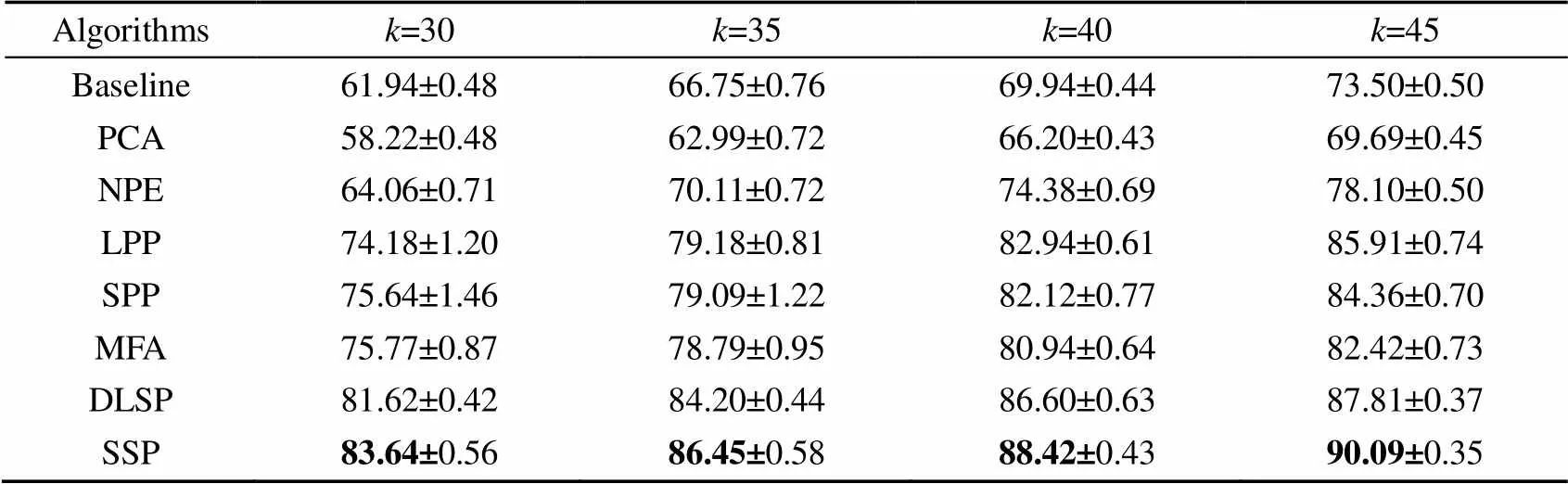
表2 CMU PIE人脸库中各算法总体识别率的最高值及其方差(平均值±方差)

4 结 论

本文基于稀疏表示和LLP提出了稀疏相似嵌入算法(SSP)，对人脸图像进行特征提取。同其它流形学习算法(如LPP、NPE等)相比，SSP算法通过稀疏表示能较好地揭示出各数据点在全局结构中的相似性，可自适应地选取数据间的近邻关系，受局部几何结构影响较小，并在低维嵌入空间中保持这种相似性不变，能更有效地提取出低维鉴别特征。在Extend Yale B人脸数据库和CMU PIE人脸数据库上进行识别率实验，结果表明本文方法比PCA、NPE、LPP、SPP、MFA、DLSP特征提取的效果都好，验证了SSP算法有效性。

[1] KIM K I，JUNG K，HANG J K. Face Recognition Using Kernel Principal Component Analysis [J]. IEEE Signal Processing Letters(S1070-9908)，2002，9(2)：40-42.

[2] LU J，PLATANIOTIS K N，VENETSANOPOULOS A N. Regularization Studies of Linear Discriminant Analysis in Small Sample Size Scenarios with Application to Face Recognition [J]. Pattern Recognition Letters(S0167-8655)，2005，26(2)：181-191.

[3] TENENBAUM J B，SILVA D V，LANGFORD J C. A Global Geometric Framework for Nonlinear Dimensionality Reduction [J]. Science(S0036-8075)，2000，290(5500)：2319-2323.

[4] ROWEIS S T，SAUL L K. Nonlinear Dimensionality Reduction by Locally Linear Embedding [J]. Science(S0036-8075)，2000，290(5500)：2323-2326.

[5] BELKIN M，NIYOGI P. Laplacian Eigenmaps for Dimensionality Reduction and Data Representation [J]. Neural computation (S0899-7667)，2003，15(6)：1373-1396.

[6] DORNAIKA F，ASSOUM A. Enhanced and Parameterless Locality Preserving Projections for Face Recognition [J]. Neurocomputing(S0925-2312)，2013，99(1)：448–457.

[7] GUI Jie，SUN Zhenan，JIA Wei，. Discriminant Sparse Neighborhood Preserving Embedding for Face Recognition [J]. Pattern Recognition(S0031-3203)，2012，45(8)：2884–2893.

[8] NGUYEN T，KHOSRAVI A，CREIGHTON D，. Spike Sorting using Locality Preserving Projection with Gap Statistics and Landmark-based Spectral Clustering [J]. Journal of Neuroscience Methods(S0165-0270)，2014，238：43–53.

[9] QIAO Lishan，CHEN Songcan，TAN Xiaoyang. Sparsity Preserving Projections with Applications to Face Recognition [J]. Pattern Recognition(S0031-3203)，2010，43(1)：331–341.

[10] LIU Qian，LAN Chao，JING Xiaoyuan，. Sparsity Preserving Embedding with Manifold Learning and Discriminant Analysis [J]. IEICE Transactions on Information & Systems(S0916-8532)，2012，95-d(1)：271-274.

[11] ZHAO Cairong，LAI Zhihui，MIAO Duoqian，. Graph Embedding Discriminant Analysis for Face Recognition [J]. Neural Computing & Applications(S0941-0643)，2014，24(78)：1697-1706.

[12] ZHANG Fei，ZHANG Jiangshe. Discriminative Learning by Sparse Representation for Classification [J]. Neurocomputing (S0925-2312)，2011，74(12/13)：2176–2183.

Face Recognition Based on Sparse Similarity Preserving Algorithm

FENG Hailiang，WAGN Yingjian，LUO Fulin

( Key Laboratory on Opto-Electronic Technique and Systems of Ministry of Education, Chongqing University, Chongqing 400044, China )

The Locality Preserving Projection (LPP) algorithms have been extensively applied for feature extraction of high dimensional face images, but selecting the neighborhood size and defining the affinity weight have a significant impact on the efficiency of LPP algorithms. In this paper, a new sparse manifold learning method was proposed, called Sparse Similarity Preserving (SSP), for dimensionality reduction of face images. It adaptively selected the similarity relation in the global structure of the data and constructed non-negative sparse graph using the sparse coefficients which reserved the global sparsity and non-linear manifold structure of face images, effectively extracting the low dimensional discriminant features. Experiments on two popular face databases (Extended Yale B, and CMU PIE), whose recognition rate reached 87.35% and 90.09%, demonstrated the effectiveness of the presented SSP algorithm.

face recognition; locality preserving projection; sparse graph; sparse similarity preserving

1003-501X(2016)06-0019-06

TP391

A

10.3969/j.issn.1003-501X.2016.06.004

2015-07-08；

2015-12-16

国家自然科学基金(61101168)；中国博士后科学基金(2012M511906，2013T60837)

冯海亮(1962-)，男(汉族)，陕西泾阳人。教授，博士，主要研究方向为信息获取与处理领域流形学习算法、模式识别算法的理论及其应用研究。

王应健(1989-)，男(汉族)，河南商城人。硕士研究生，主要从事数字图像处理，模式识别。E-mail：fhliang@cqu.edu.cn。