GPU加速的高精度位移估计方法及超声弹性成像应用

彭 博，黄 丽



GPU加速的高精度位移估计方法及超声弹性成像应用

彭 博，黄 丽

( 西南石油大学 计算机科学学院，成都 610500 )

高精度的位移估计方法对提高超声弹性成像的质量非常重要。在本研究中，通过英伟达公司的CUDA架构实现了一种新颖的可以同时提高轴向和横向运动估计精确度的位移估计方法在GPU上的高效并行计算。对比于原始方法在C Mex编译条件下的实现，GPU实现的方法显示最多可实现76X的加速，同时保持了较高的位移估计精度。

超声弹性成像；运动追踪；子采样位移估计；图形处理器；CUDA

0 引 言

基于超声的弹性成像技术是一种非常有前途的成像模式，它可替代触诊来评估人体组织弹性模量的变化，是传统超声成像技术的有益补充。在超声弹性成像过程中，首先追踪变形前后的两帧RF信号之间的位移，然后通过对位移进行差分操作获得应变信息来表征组织的弹性信息。通常在许多人体器官系统中，正常组织与非正常组织的弹性模量具有非常大的差异，这使超声弹性成像技术成功的应用在鉴别良性或恶性乳腺肿瘤[1-2]，监视肝肿瘤的热消融治疗[3-4]等病症的临床治疗和诊断中。

高精度的轴向与横向位移可以提高超声弹性成像技术的准确度。然而，在普通的超声弹性成像系统中，通常不具有横向位移估计功能或获得的横向位移估计精度远低于轴向位移估计精度。近来Jiang提出了一种可直接采用临床成像系统获得的超声回波数据进行散斑追踪并能同时获取高精度轴向和横向散斑追踪结果的替代算法[5](以下简称Coupled子采样位移估计算法)。该算法基于医学超声成像系统的线性系统理论，通过推导变形前后的回波信号之间的互相关函数，其演示了log压缩的互相关函数的等高线是一系列椭圆并共享同一个中心。这些椭圆的中心正对应着互相关函数峰值。通过确定这些椭圆的中心就能同时获取轴向和横向位移。对比传统的运动追踪方法，该算法在计算机模拟体模、仿真组织体模和活体数据下，都获得了非常高的轴向与横向子采样位移估计精度[5]。虽然该算法具有非常突出的位移估计性能，但是在CPU的计算环境下，其计算效率不高[5]，这使得该算法的临床应用受到极大的限制。

当前GPU软硬件的发展给超声弹性成像技术带来了更多的机会与动力，本文的研究目的主要是利用GPU多核处理器架构实现“Coupled子采样位移估计算法”的高效并行计算。通过分析该算法易于并行处理的特性，利用CUDA架构实现该算法，从而达到通过GPU并行计算满足该算法的实时计算的需求。

1 方 法

1.1 “Coupled子采样位移估计算法”框架

二维块匹配方法[6]是一种常用于超声散斑运动追踪的方法，它的基本思想是将变形前RF信号帧分成许多宏块，然后对每个宏块在变形后RF信号帧中在给定特定搜索范围内根据一定的匹配准则(如互相关函数)找出与当前块最相似的块，即匹配块，匹配块与当前块的相对位移即为运动矢量。当采用互相关函数作为匹配准则时，由于互相关函数的最大值位置代表了变形前RF信号帧中某一宏块在变形后RF信号帧中对应的位置，因此传统的处理方法只关心最大值及其位置，实际上并没有充分利用其它在搜索范围内已经计算出来的互相关函数值。

通过医学超声系统的线性系统理论[7]，非常容易演示在上述运动追踪过程中，变形前后的两帧RF信号在通过互相关函数计算时，延时其log压缩的互相关函数峰值附近可表示为

这里，1和2是相关于超声系统的参数，通常为常数。D和D表示一个均匀的网格，可以得到一个对应的二维互相关系数矩阵。式(1)指出，在互相关的峰值附近，基于log压缩的互相关能被近似为一个二阶的多项式表面。因此子采样位移追踪的目的就是发现对应于互相关函数的真正最大值的位置。拟合互相关系数峰值附近的互相关系数值来估计位移有一阶和二阶曲线两种方法。但“Coupled子采样位移估计算法”不同于拟合曲线方法，它将需要拟合的互相关系数看成是一个椭圆。通过定位椭圆中心等价于寻找互相关函数的理论峰值，也就是当和，互相关函数获得最大值。简而言之，这个方法首先选择互相关峰值附近的一个互相关系数值，然后选择作为等高线的值并拟合为一个椭圆，拟合得到的椭圆中心点在数学角度上等于未知子采样位移。

1.2 “Coupled子采样位移估计算法”的实现

“Coupled子采样位移估计算法”包含四个步骤：1) 采用标准的二维块匹配算法进行初始的整数位移估计，实现细节可参考[6]；2) 利用步骤1得到的整数位移对变形后的RF信号帧进行运动补偿，提高计算互相关系数的相关性。在一个新的搜索区域上如[-3:0.5:3,垂直方向]´[-3:0.5:3,水平方向]计算新的互相关函数矩阵；3) 选择合适的等高线值计算该等高线上位置的坐标；4) 拟合所选择的等高线的坐标成一个椭圆[8]，椭圆方程中的中心点坐标就是子采样位移矢量。在第三步中，等高值的计算式[5]为

1.3 GPU编程环境

GPU编程环境下的并行计算编程可简单分为两个阶段：1) 计算任务并行化，即是同时启动多个GPU线程进行计算以提高计算效率，这是算法可并行计算的必要条件。2) 访存优化，与CPU编程环境下不同，GPU编程环境下对于访存优化的要求更高。当前在英伟达的CUDA编程架构中，合理使用高速存储器(寄存器，共享内存)是提高GPU程序执行效率的一种有效手段[10-11]。除了寄存器和共享内存，常量存储器和纹理映射也是一种提高访存效率的有效内存访问手段。

1.4 “Coupled子采样位移估计算法”的GPU实现

“Coupled子采样位移估计算法”在块匹配方法的框架下实现并行计算。在实现过程中，通过以下几个策略来提高该算法的计算效率。第一，在互相关函数的计算中，轴向的互相关窗口长度和互相关窗口中的回波线数量及轴向的重叠率，这些参数决定了位移估计点数量。假定最终得到位移图像包含rows行和cols列，rows和cols表示搜索区域的尺寸，由于这些估计点的计算过程不需要互相通信。相应的kernel函数可以启动(rows´cols)´(rows´cols)个GPU线程满足算法并行执行的需求。为保证内存访问的一致性，即相邻的线程访问相近的内存区域，尽量满足合并内存事务而采用一维的线程结构。第二，RF数据的存储到纹理内存，英伟达GPU的纹理内存技术通过硬件加速数据的插值过程，避免了计算非整数位置时的插值过程。最后，一些重要的变量(如轴向与横向搜索范围，互相关计算核尺寸)存储到GPU常量内存中，以实现快速访问。

在CUDA编程结构中，kernel函数实际就是SIMD(单指令多数据)的实现过程。而device函数可以认为就是一个单线程函数。因为每一个估计点的计算是独立的，因此，每一步计算过程中kernel函数的线程配置都可以启动(rows´cols)个GPU线程满足算法并行执行的需求。第一步与第二步中搜索区域(rows´cols)上的互相关系数值计算可实现完全的并行计算，这两步的并行计算程度较高。第三步与第四步中计算等高线上位置的坐标的过程与拟合椭圆并求解该椭圆方程的过程均设置为device函数，并在线程配置为(rows´cols)的kernel函数中调用，这两步的并行计算程度较低。

1.5 应变计算

超声弹性成像的应变来源于对位移计算差分，轴向与横向应变的估计公式为和。局部轴向应变和横向应变的计算通过一个低通数字差分滤波器实现[12]。

1.6 验证

本研究中，计算平台的操作系统为Windows 7 64-bit，计算CPU为Xeon E3-1220 V2 CPU @3.1GHz，计算GPU为NVIDIA Telsa K20c，主机内存为8 GB。

仿真模拟数据集使用文献[13]中提出的模拟压缩前后的生物组织变化数学模型模拟获得。仿真的散射子模型内部包含一个硬球，模型的宽度为4 cm，深度为4 cm，硬球的半径为0.5 cm，位于模型内部中间位置。这个模型由200 000散射子构成，散射子的强度符合高斯分布。

体模实验采用CIRS公司(诺福克，弗吉尼亚州，美国)专用于弹性成像研究的Model 049弹性体模。实验使用的超声系统是iMago C21超声机(Saset医疗保健公司，成都，中国)，系统RF信号采样频率设为40 MHz。实验使用的探头型号为SA5L38B的128阵元的线阵探头，中心频率为5 MHz，75%分数阶带宽。实验中成像对象为弹性体模中直径为10 mm、弹性模量是63 kPa的硬包容物(Type IV)。在数据采集过程中未使用任何额外控制设备，徒手保持一恒定的速度将探头进行轴向压缩/释放。

2 结 果

表1显示了计算不同大小位移图像时，CPU和GPU实现的计算时间。对于位移估计的计算来讲，单精度浮点数已经足够，因此本文中所有的GPU实现都默认为采用单精度浮点数。其中与计算效率相关的主要参数值分别为，互相关窗口为61´11，整数位移的搜索范围为[-5:1:5]´[-5:1:5]，子采样互相关函数的计算范围为[-3:0.25:3]´[-3:0.25:3]。从表1可以得出，本文所实现的GPU方法计算效率得到了较大的提高，GPU方法最多获得了76X的加速。

表1 GPU实现与CPU实现的计算效率比较

Table 1 Comparison of running time for two different implementations s

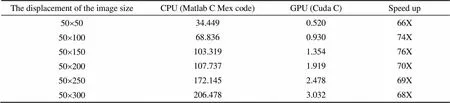
The displacement of the image sizeCPU (Matlab C Mex code)GPU (Cuda C)Speed up 50´5034.4490.52066X 50´10068.8360.93074X 50´150103.3191.35476X 50´200107.7371.91970X 50´250172.1452.47869X 50´300206.4783.03268X

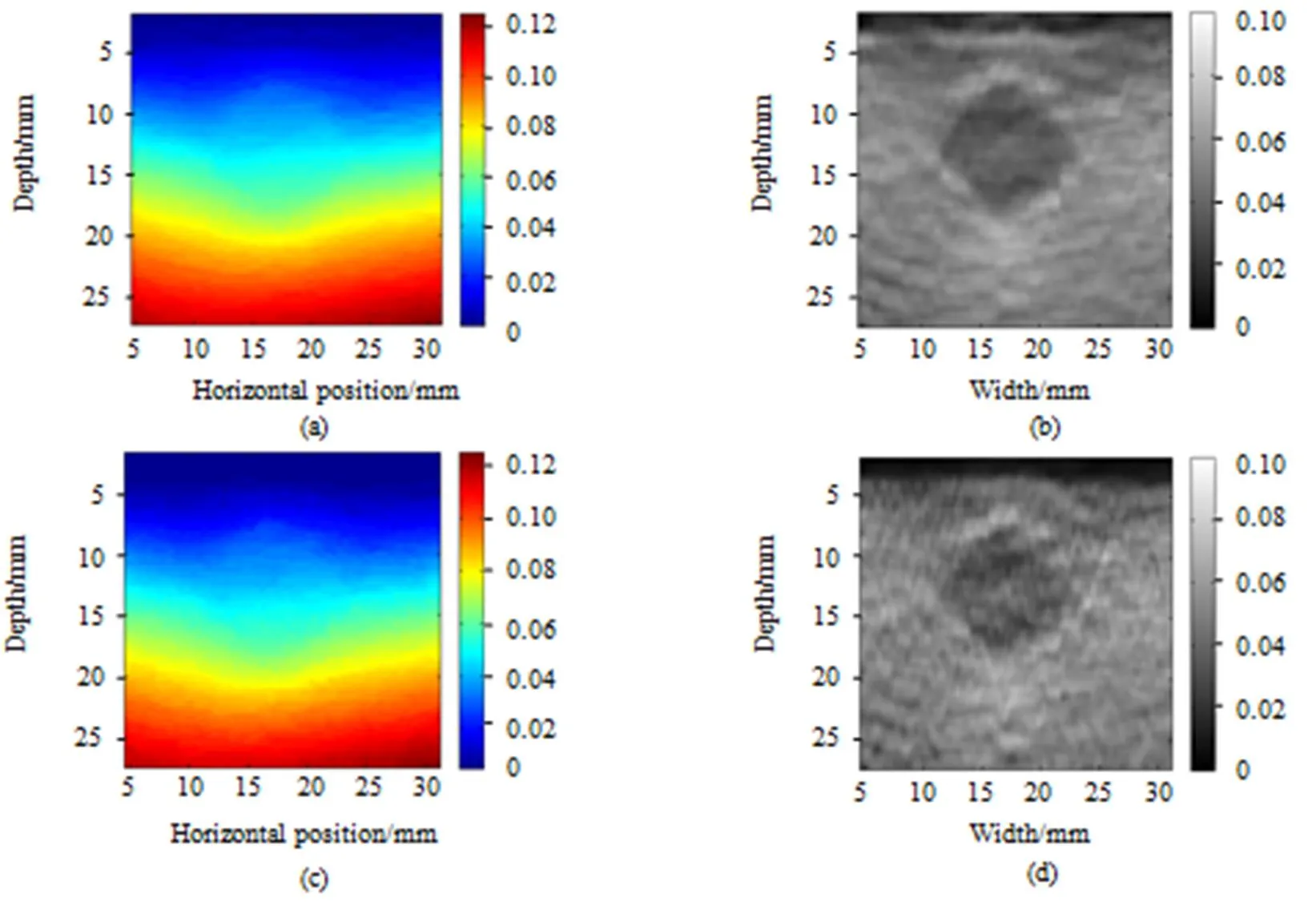
图1显示了“Couple子采样位移估计算法”与二阶抛物线拟合算法[14]在仿真组织体模下产生的位移及对应的应变图。虽然两种方法的轴向位移无明显差距，但生成的轴向应变图可以明显看到两者依然具有一些差异。

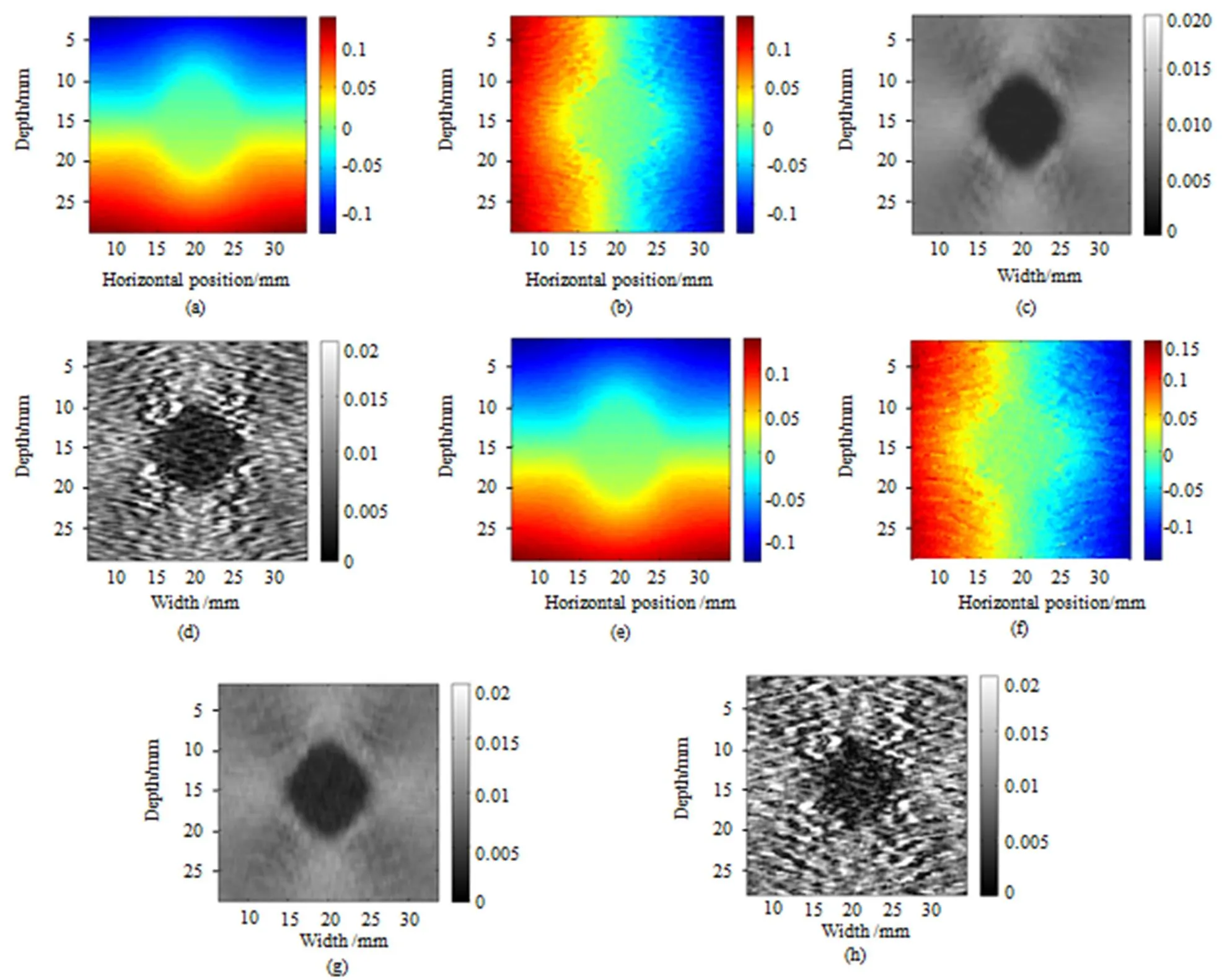
图1 仿真数据上两种方法计算得到的位移和应变对比