小学数学典型易错题分析及纠正策略

江苏盐城市第二小学（224000） 李天良

小学数学典型易错题分析及纠正策略

江苏盐城市第二小学（224000） 李天良

在数学学习过程中，学生不可避免会做错题，此时，教师应引导学生认真审视，深入剖析，理性反思，从中探寻出错误的根源，进而对症下药，及时改正，提高学生的数学解题能力。

小学数学易错题纠正对策

小学生由于受年龄特点、知识经验、认知水平、思维能力的限制，在解数学题的过程中不可避免地会出现各种错误。因此，教师要正确对待学生的错误，因势利导，巧妙地将学生的错误作为一种有效学习资源，引导学生认真审视、深入剖析、理性反思错误，探寻错误的根源。

一、审题偏差类——审题不当，出现认知偏差

【案例1】为增强居民节约用电意识，某市居民生活用电采用阶梯式计费，收费标准如下表所示：

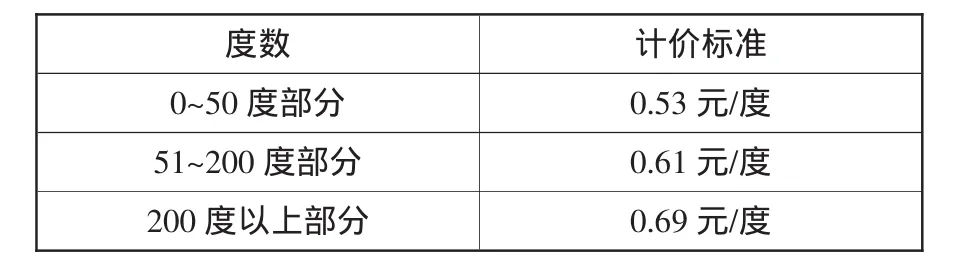
度数　计价标准0～50度部分　0.53元/度51～200度部分　0.61元/度200度以上部分　0.69元/度

王林家八月份用电量是275度，请计算他家八月份应缴纳电费多少元？（得数保留一位小数）

错解：275×0.69≈189.8（元）。

答：王林家八月份应缴纳电费181.5元。

错因聚焦：出现错解的原因主要在于学生审题时出现了认知偏差，未能深刻领会阶梯式计费的实际含义。实际上，275度可以分为3个部分，即50度、150度和75度，故需缴纳电费50×0.53+150×0.61+75×0.69≈169.8（元）。

纠正对策：有效审题是准确解题的前提和关键。在平时教学中，教师要重视学生审题能力的培养，注意引导学生细致审题，认真读题，明确题意，抓住题目中的关键字、词或句，仔细推敲，准确理解其表达的意义，找准其数量关系，挖掘隐含条件，形成良好的审题习惯，从而准确、有效、快速解题。

二、概念模糊类——对数学概念模糊，理解不透彻

【案例2】1.68千克黄豆可榨油0.55千克，那么1千克黄豆可榨油多少千克？榨1千克油需要多少千克黄豆？（得数保留两位数）

错解：1.68÷0.55≈3.05（千克），

0.55÷1.68≈0.33（千克）。

答：1千克黄豆可榨油3.05千克。1千克油需要0.33千克黄豆。

错因聚焦：错解产生的原因是学生对“平均数”这一数学概念理解不透彻，掌握不牢固，对于“把什么东西平均分”、“平均分成几份”混淆不清，因而在解题时只是胡乱将两个数字相除，从而导致错解。

正解：0.55÷1.68≈0.33（千克），

1.68÷0.55≈3.05（千克）。

答：1千克黄豆可榨油0.33千克。1千克油需要3.05千克黄豆。

纠正对策：鉴于以上错解，教师在进行平均数教学时，应引导学生关注平均分的过程，重点把握“把什么东西平均分”、“平均分成几份”的含义。同时，要加强对平均分现象的剖析，通过典型实例引导学生适时构建数学模型，进而透过现象看本质，把握平均分的本质特征，找出数与数之间的内在联系，从而建立数量关系，巧妙解题。

三、思维定式干扰类——思维惯性的束缚，误导问题解决

【案例3】请你先用纸把一串数字“1000，40，1000，30，1000，20，1000，10”盖起来，然后把纸逐渐往右移，一次只露出一个数字，边移动边口算这些数字的和，如1000，40…依次类推，直到最后一个数字，请问你的答案是多少？

错解：5000。

错因聚焦：由于边移动边口算，就会一直重复着“1000”，“2000”，“3000”，“4000”，受思维定式的影响和干扰，学生就会产生思维惯性和盲点，致使许多学生会不假思索，直接脱口而出“5000”。

纠正对策：思维定式是影响解题的重要因素，在平时教学中，教师要加强学生的思维训练，鼓励学生大胆探索、联想，敢于标新立异，另辟蹊径，不拘泥于一种解题思路或解题模式，多角度、多层次、多方位地思考和分析问题，以探求更巧妙的解题方法，从而帮助学生打破思维常规，培养学生思维的灵活性和变通性，提高学生多向思考的能力。

总之，教师要深入分析学生解错题的原因，明晰错误类型，灵活对待学生的错误，并采取相应的纠错策略，帮助学生找错、议错、辨错、纠错，让学生知其错，且知其所以错，从而提升学生的防错能力，增强学生的数学解题能力。

（责编童夏）

G623.5

A

1007-9068（2016）26-046