斜拉桥的极限跨径分析
邓小康,彭 蓉,李永明
(1.武汉市市政工程质量监督站,湖北 武汉 430010;2.广西交通科学研究院,广西 南宁 530007)
斜拉桥的极限跨径分析
邓小康1,彭蓉2,李永明1
(1.武汉市市政工程质量监督站,湖北武汉430010;2.广西交通科学研究院,广西南宁530007)
文章从斜拉索强度、主梁强度等静力性能方面对斜拉桥的极限跨径进行探讨,以苏通长江大桥为例对斜拉桥离索塔最远拉索的受力情况进行了详细分析,并计算出该情况下的斜拉桥极限跨径,同时采用笔者编制的程序对靠近主塔的主梁根部位置进行轴向受力分析,得出了主梁强度是限制斜拉桥跨径增大的关键因素的结论。
斜拉桥;极限跨径;高跨比;索距;斜拉索强度;主梁强度
0 引言
超大跨度桥梁结构必须以缆索承重体系为主,这已经成为结构工程师的共识,而与悬索桥相比,斜拉桥在抗风稳定性、经济性、特别是适应恶劣地质条件等方面优势明显,因此在超大跨径桥梁方案比选时,斜拉桥成为最有竞争力的桥型。尤其是在近二十年来,斜拉桥取得了划时代的长足进步,其最大跨径由300~400 m发展到超过1 000 m,这主要得益于材料性能的提高、工程实践水平的发展以及桥梁设计计算理论的完善。
伴随着斜拉桥的不断发展,确定斜拉桥的极限跨径和经济跨径是一个首先要考虑的问题,国内外虽然许多著名专家学者都曾试图推算出斜拉桥的极限跨径和经济跨径,并取得了一定的成果,如中国的李国豪教授曾经指出,斜拉桥的最大跨径主要取决于缆绳刚度,据此解出斜拉桥的最大跨径可达3 600 m;王伯惠也曾对此问题做过专门分析[1][2]。但这些分析采用的近似计算太多,成果多是在20世纪取得,随着材料学和工程学的发展,有必要对这些分析进行改进。笔者即结合当前斜拉桥最新的发展情况从斜拉索强度、主梁强度等静力性能方面对斜拉桥的极限跨径做进一步探讨。
1 斜拉索强度对极限跨径的影响
1.1斜拉索的受力分析
从斜拉桥的受力特性可以看出,离索塔最远的那根拉索受力情况最为不利。在不考虑垂度效应及非线性时,将斜拉索看作一根受拉刚性直杆,离索塔最远的那根斜拉索的受力情况如图1所示。

图1 离索塔最远的斜拉索的受力示意图
对于密索体系,原则上认为每根拉索承担一个索距节段上的恒载、活载和拉索自重的一半[1],由力的平衡关系可得:
(1)
其中T——离索塔最远的那根斜拉索的拉力;
WD——一个索距节段上作用的恒载;
WL——一个索距节段上作用的活载;
WT——斜拉索的自重。
同时,由斜拉桥的力学和几何特性可得:
T=σcAc
(2)
WD=gλ
(3)
WL=qλ
(4)
(5)
(6)
(7)
其中:σc——斜拉索的应力;
Ac——斜拉索的截面面积;
g——节段上作用的恒载集度;
q——节段上作用的活载集度;
λ——索距;
γc——斜拉索的重度;
Lc——主跨跨径;
h——索塔的有效高度;
e——斜拉桥的塔高跨比。
联立上述(1)~(7)式,可得:
(8)
(9)
1.2参数拟定
针对公式(9)所涉及的参数进行详细分析[3]。
(1)斜拉桥的塔高跨比e
斜拉桥的塔高跨比一般为0.2~0.25,为便于分析,考虑到本文所探讨的为超大跨径的斜拉桥,因此将其取为较小值0.2。
(2)斜拉索的固有特性Ac、σmax、γc
当前斜拉索主要采用平行钢丝斜拉索和钢绞线斜拉索两种,其中绝大多数使用的是平行钢丝拉索。为方便分析,笔者选取国内已建成的跨径最长的斜拉桥——苏通长江大桥斜拉索的固有特性进行分析。苏通长江大桥采用的平行钢丝拉索最长达到577 m,最大重量为59 t,单根拉索最大截面面积为120 cm2(计算时按双索面考虑),平行钢丝的抗拉强度最大为1 770 MPa,线密度约为100.29 kg/m[1]。按公路斜拉桥设计规范将安全系数取为2.5时,则σmax=708MPa。Ac=0.012 m2,Acγc=100.29 kg/m。
(3)λ、g、q
结合当前国内大跨径斜拉桥设计、施工的情况,本文选取λ=15m进行研究。
另根据苏通长江大桥的情况,并考虑适当的放大,取g=2.5×105N/m,q=7×104N/m。
1.3计算结果
将上述参数带入公式(9),可以得到当前状况下斜拉桥极限跨径为5 708 m。
2 主梁强度对极限跨径的影响
为便于计算,笔者仅对主梁为钢箱梁的情况进行计算分析。对于主梁的轴力,采用“平均索法”计算[1],如图2所示,将半个主跨的拉索集中成一根平均索,该索在梁上锚于L/4的位置,承担该半跨的全部荷载。

图2 平均索法求水平分力示意图
由力的平衡关系和斜拉桥的几何特性可得:
(10)
N=T·cosα
(11)
综合式(10)、(11)可得:
(12)
N=ηaA0[σ]
(13)
其中ηa为主梁截面面积增大系数,取为ηa=1.25;A0为主梁截面面积,参考当前斜拉桥的设计施工情况,取为A0=3 m2;[σ]=200MPa。
联立式(12)、(13)可得:
(14)
取e=h/L可得:
(15)
参照第一节的分析,WD=gL/2=2.5×105·L/2,WL=qL/2=7×104·L/2。
对于WT,由图3可得:
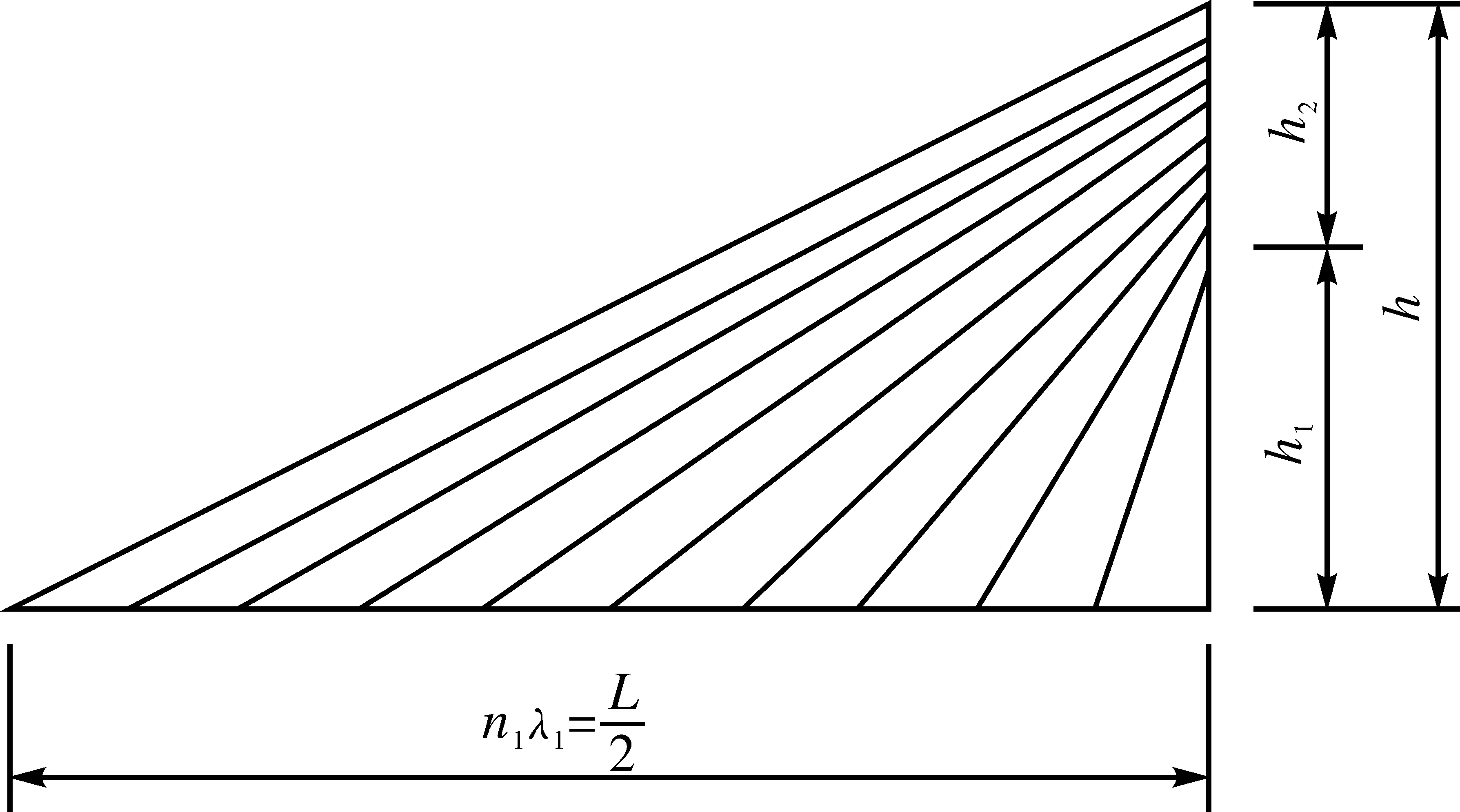
图3 半跨斜拉桥的拉索实际分布示意图

(16)
其中Acγc=100.29 kg/m=982.842 N/m。
整理上述公式可得:

对于上述公式,采用自编程序对n1从100到300(即跨径从1 500 m到4 500 m)进行试算发现,当n1=185时,两边等式最接近。
可以看出,当主梁面积A0=3 m2,梁的高跨比取为0.2,梁上索距取为15 m,塔上索距取为2.8 m,主梁容许应力为200 MPa时,斜拉桥的极限跨径为2 755 m。
3 结语
综上所述,可以得到以下结论:
(1)在只考虑静力作用时,限制斜拉桥的跨径增大的关键因素是主梁的强度,在文中所设条件下,受主梁强度影响,斜拉桥的极限跨径仅2 755 m;
(2)斜拉桥的高跨比、塔上和梁上索距等参数对斜拉桥的极限跨径有着决定性的作用,大跨径的斜拉桥必然伴随主塔高度的增高和斜拉索索距的减小;
(3)斜拉桥的主梁挠度、稳定性和各项动力性能
对斜拉桥跨径的增大也起着决定性的作用,应做进一步的探讨。
[1]王伯惠.斜拉桥的极限跨径(连载一)[J].公路,2002(3):46-53.
[2]王伯惠.斜拉桥的极限跨径(连载二)[J].公路,2001(4):38-48.
[3]孟庆威,齐欣,等.千米级斜拉桥斜拉索相关参数计算方法[J].桥梁建设,2009(2):58-60.
[4]徐利平.超大跨径斜拉桥的结构体系分析[J].同济大学学报:自然科学版,2003,31(4):400.
[5]刘志文,陈艾荣,周志勇,等.大跨径斜拉桥斜拉索静风荷载计算方法比较[J].同济大学学报:自然科学版,2005,33(5):575.
[6]苏庆田,吴冲,董冰.斜拉桥扁平钢箱梁的有限混合单元法分析[J].同济大学学报:自然科学版,2005,33(6):742.
[7]程进,江见鲸,肖汝诚,等.ANSYS二次开发技术及在确定斜拉桥成桥初始恒载索力中的应用[J].公路交通科技,2002,19(3):50.
[8]苗家武,肖汝诚,裴岷山,等.苏通大桥斜拉桥静力稳定分析的综合比较研究[J].同济大学学报:自然科学版,2006,34(7):869.
[9]颜东煌.斜拉桥合理设计状态确定与施工控制[D].长沙:湖南大学,2001.
Limit Span Analysis of Cable-stayed Bridges
DENG Xiao-kang1,PENG Rong2,LI Yong-ming1
(1.Wuhan Municipal Engineering Quality Supervision Station,Wuhan,Hubei,430010;2.Guangxi Transportation Research Institute,Nanning,Guangxi,530007)
This article discussed the limit span of cable-stayed bridges from the aspects of stayed cable intensity,main beam intensity and other static properties,and with Sutong Yangtze River Bridge as the example,it conducted the detailed analysis on the force situation of the cable furthest away from the cable tower in cable-stayed bridge,and calculated the limit span of cable-stayed bridge under such situation,while using the program prepared by the author to conduct the axial stress analysis at the main beam root position close to main tower,and then obtained the conclusion that the main beam intensity is the key factor to limit the span increase of cable-stayed bridges.
Cable-stayed bridge;Limit span;Depth-span ratio;Cable distance;Stayed cable intensity;Main beam intensity
U448.27
A
10.13282/j.cnki.wccst.2016.08.012
1673-4874(2016)08-0046-03
2016-06-02
邓小康(1985—),博士研究生,工程师,主要从事市政工程质量监督工作;
彭蓉(1985—),工程师,研究方向:桥梁检测与加固设计;
李永明(1986—),硕士研究生,助理工程师,主要从事市政工程质量监督工作。

