利率期限结构的突变效应：多结构变点协整分析

韩国文，邓颖婷



利率期限结构的突变效应：多结构变点协整分析

韩国文，邓颖婷

(武汉大学经济与管理学院，湖北武汉，430072)

基于预期理论，运用多结构变点协整回归模型检验利率期限结构。通过考察2002年1月至2014年12月间的长期利率与短期利率，发现在多结构变点存在的前提下，动态OLS协整检验发现长、短期利率之间存在长期协整关系。计算得出的协整向量与理论值有一定差距，说明预期理论仅局部成立。多结构变点检验显示，在样本期间，利率期限结构总共发生了四次结构变点，解释变量的系数符号也发生了反复改变。经过分析发现，宏观经济走势、利率市场化改革、汇率波动以及2008年的全球金融危机是结构变点存在的重要原因。

利率期限结构；多结构变点；预期理论；动态最小二乘法

一、引言与文献综述

在当前全球实体经济持续疲软，金融市场动荡加剧，国际货币政策分化，中国经济进入“新常态”的背景下，利率作为货币政策的主要工具之一，对合理引导预期为实体经济结构调整争取时间和空间、激发更多内生增长动力有重要作用。央行可以通过观察利率期限结构来了解市场参与者的预期和货币政策的实施成效，进而制定相应措施，实现货币政策调控的灵活性、前瞻性、稳定性和精准性。孙浩和石柱鲜[1]、顾亚露等[2]、王志强等[3]分别采用宏观−金融模型、SVAR模型、STR模型研究了利率期限结构与宏观经济增长之间的关系，发现利率期限结构包含了大量宏观经济信息，涉及货币政策、经济增长、利率变化等。利率期限结构是人们判断经济形势，进行金融决策和对金融工具定价的重要依据，其特性已成为理论界与实务界最热门的研究问题之一。

预期理论认为在不存在期限偏好、交易费用但存在理性预期的前提下，长期债券的到期收益率应当等于长期债券到期之前的短期利率预期的平均值。因此，若预期理论成立，那么不同期限的利率将随着时间的推移而发生协同变化，即长、短期利率之间存在着长期的协整关系向量(1，−1)，彼此之间的利差亦存在均值回归。基于这一理论，可以通过检验长、短期利率之间是否存在协整关系以验证预期理论。

Campbell和Shiller[4]采用协整VAR模型检验美国利率期限结构，发现美国长、短期利率之间存在协整关系，他们的研究奠定了最近30年研究利率期限结构预期理论的基础。Sarno等[5]通过拉格朗日乘数法在模型中引入了多种期限利率，提高了检验的有效性。传统上对预期理论的验证多采用线性模型，Esteve[6]在2006年根据门限协整法建立了非线性模型，发现长、短期利率之间的协整关系在非线性模型中不成立，从而确认了线性模型在预期理论检验中的适用性。

由于宏观经济的周期性波动，利率变动可能存在多结构变点，因此有学者开始研究基于结构变点的长、短期利率之间的关系。Camarero和Tamarit[7]首先将结构变点和不稳定性引入协整回归，并提出三种检验协整回归中结构变点和不稳定性的方法：拉格朗日乘数检验、单结构变点检验、基于OLS的多结构变点检 验[8]。其中，最后一种检验能有效克服前两种检验的缺点：第一，样本数目较少、解释变量边际分布存在结构变化时，功效较低；第二，只能用单结构变点。研究结果表明，在西班牙，长期利率和短期利率的协整关系成立。Suardi[9]、Esteve等[10]利用多结构变点方法分别采用澳大利亚和西班牙的数据检验利率期限结构预期理论，结果显示预期理论成立。显然，引入结构变点后，预期理论的检验效果提高不少。

国内的一些学者也对长、短期利率之间的关系进行了研究，然而对预期理论是否在国内成立各执一词。例如吴丹和谢赤[11]采用自回归模型及向量自回归模型、李宏瑾[12−13]采用协整模型及期限溢价修正模型对我国利率进行分析，结果显示预期理论成立。张雪莹等[14]采用VAR模型对我国利率进行分析，结果显示预期理论不成立。王志强和熊海芳[15]在时变期限溢价的基础上采用结构变点方法研究长、短期利差对短期利率变动的解释能力。实证结果显示模型存在多个结构变点，不同区间内预期理论基本上被拒绝。但他们的研究所采用的数据为银行同业拆借利率，最长利率期限为120天，缺乏代表性。

过去15年中国经济处于不断变革之中，许多经济变量表现出结构性变化的特征，因此应当通过多结构变点法来确认结构性变化。通过研究长、短期利率之间的关系，我们可以发现利率期限结构中包含的深度信息，为货币政策的制定和执行提供建议。本文对利率期限结构特性的研究从以下三个方面进行了拓展：第一，采用多结构变点方法和动态最小二乘法，能够更准确地检验参数的不稳定性、变点个数，并对解释变量的内生性、OLS估计的误差项进行修正；第二，采用新的数据，并将样本区间扩展为2002年至2014年，使时间长度更符合统计学中要求的大量观测值；第三，从新的角度考察了我国利率市场化改革的成效，并分析了汇率制度改革、全球金融危机对利率期限结构的影响。

二、实证模型和实证方法

(一)利率期限结构的预期理论模型

根据预期理论，长期利率和短期利率之间应当存在较为稳定的关系，并进而决定利率期限结构的形状。基于Taylor[16]、Bekaert和Hodrick[17]的研究，利率期限结构预期理论的基本模型如下：长期利率=当前短期利率、未来短期利率预期的均值+代表期限/风险溢价的常数项，即

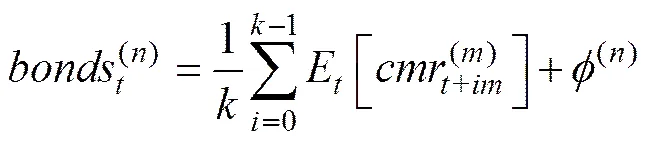
为了方便检验利率期限结构的预期理论，(1)式也可用线性模型表示为：

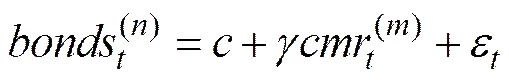
Campbell和Shiller认为bonds、cmr之间存在协整关系，协整向量为(1，−1)，且利差存在向均值回归的趋势。如果利差固定，则期限/风险溢价也是固定的，不同期限的利率会由一个随机变量主导(例如通货膨胀率)，以防过度偏离均值。这一假设表明某些特定到期日的期限溢价结构能预测长期债券收益率的未来变化情况，当前利差是对未来变化的最优预测，市场对短期利率的预期将映射在期限结构的斜率上，即=1。

(二)多结构变点协整回归模型

结构变点模型是针对现实中经济结构存在非线性等问题而提出的，一般可分为外生结构变点模型和内生结构变点模型。由于外生结构变点模型存在无法克服的主观性，研究重心逐渐转向了内生结构变点模型。并且随着计算机技术和计量经济学的发展，研究逐渐从研究单结构变点拓展到了多结构变点[18]。

Kejriwal和Perron[19]提出了一个有个结构变点的模型(+1个时段)：

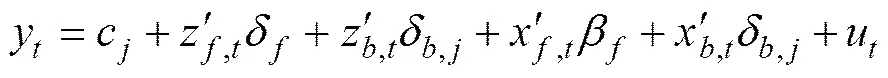
(1,2,…,m)为未知的个结构变点，将样本分成了+1段，其中0=0,T+1=。y为时期的被解释变量，是(1)（一阶差分）过程；代表回归量；代表存在变点的(1)变量的数目(包括截距项)；代表(0)(平稳)变量的数目；和代表系数向量；、分别代表有结构变化的部分和不变化的部分；为误差项。x,t(p×1)和x,t(p×1)是解释变量，是(0)过程；z,t(p×1)和x,t(p×1)是解释变量，是(1)过程。

在模型(3)中，设只有特定的回归量参数可发生变化。在本文中，即为p=p=q=0。并设所有(1)回归量和常数项[模型(2)中的斜率与截距项]可在样本期内变化。则可得：

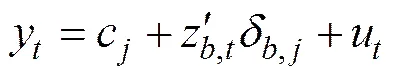
为解决(1)过程的内生性，Kejriwal和Perron提出使用动态OLS回归法(DOLS)。该方法在解释变量中加入了(1)序列的超前量和滞后量：

如果

(5)

(三)多结构变点的检验模型

本文主要采用以下四种方法进行多结构变点检验。

(1)信息准则检验(information criteria test)。Yao[20]认为在相对稳定的条件下，通过使施瓦兹信息准则(Schwarz criterion)最小化，可以获得正确的变点数目。对该方法进行改进，采用修正的施瓦兹信息准则对时间序列进行检验，可以获得更准确的结果。

(2)最小上界Wald检验(Sup Wald test)。原假设为不存在变点(=0)，备择假设为存在固定变点个数(=)：

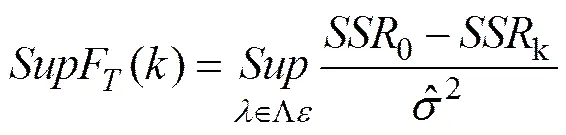
为变点部分的向量，=T/，={1，…，i，…，}，=1,…,，T为变点发生时的日期，为可取的集合。SSR0是在原假设下的残差平方和，SSR是在备择假设下的残差平方和。这一检验的核心思路是在一个设定的域内，对所有可能的变点依次取值，求Wald统计量的最大值并判断其是否显著。若SupF()显著，则所检验的序列存在个结构变点。

(3)双最大值检验(double maximum test)。令原假设为不存在变点(=0)，备择假设为有未知数目的变点。双最大值检验存在两个检验统计量，即统计量和统计量。统计量是SupF(k)统计量，其中k为变点的最大可能数目，而统计量则对单个统计量进行加权，使k取不同值时值相等。

(4)序贯检验(sequential test)。这一检验通过使残差平方和最小化来获得变点日期。令原假设有个变点，备择假设有+1个变化点，变点日期为()。检验将对按从小到大的顺序依次取值，每次将数据按照变点日期分为+1份，并对每一次的+1部分进行检验，判断统计量的最大值是否显著，若显著，则认为有+1个变点。公式如下：

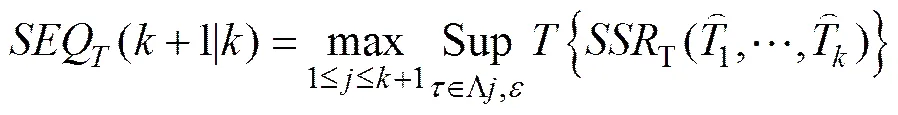
与传统序贯检验不同，的每次日期取值将重新进行估计，以准确地反映残差平方和的全域最小化。

后3种检验由Kejriwal和Perron[19]提出，与之前的结构变点检验相比，放宽了对时间序列平稳性的要求，允许(0)过程和(1)过程同时存在。

三、我国利率期限结构预期理论的实证检验

(一)数据的选取及说明

本文数据的时间跨度为2002年1月至2014年12月。基于数据的可得性和实用性，长期利率采用中央国债登记结算有限责任公司(简称“中债登”)所提供的10年期标准国债的到期收益率月度数据。由于上海银行间同业拆借利率从2007年1月4日起才开始正式运行，故2002年1月至2006年12月的短期利率数据采用1个月银行间质押式回购利率；2007年1月至2014年12月的短期利率数据采用3个月上海银行间同业拆借利率，数据来自Wind咨询数据库。与央行的基准存贷款利率相比，本文所选的短期利率在金融市场上使用范围更广，成交量更大，更具有代表性。

由图1可知，我国长、短期利率的基本变化方向一致，并且随着时间的推移，二者的变化趋势越发接近，这说明短期利率的变化对长期利率的变化影响越来越大。此外，在整个样本期间，短期利率比长期利率的波动幅度更大。

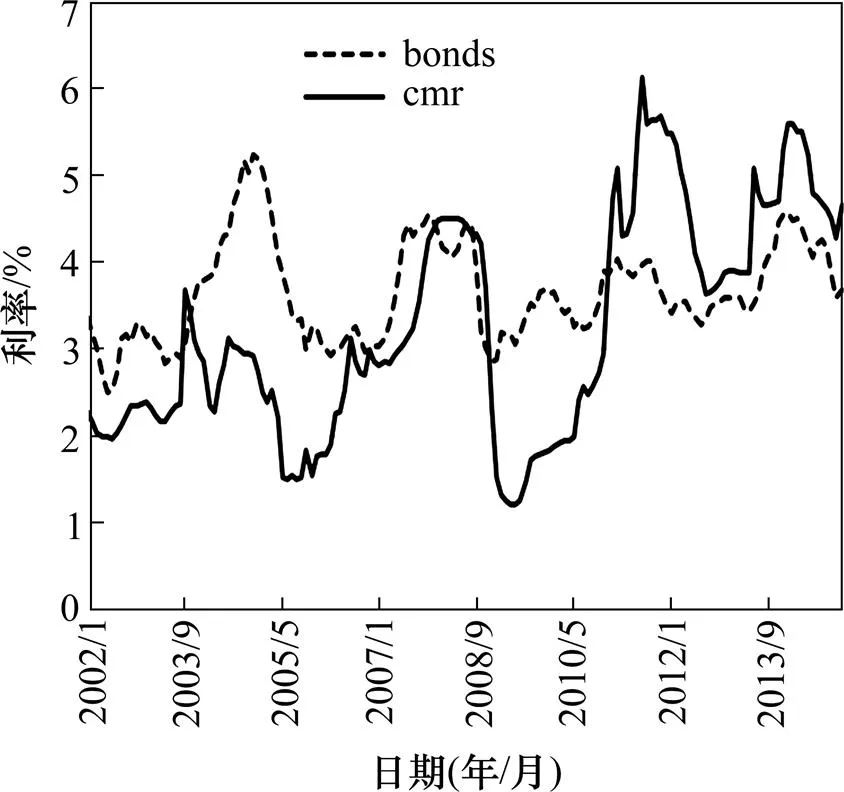
图1 中国长期利率(bonds)和短期利率(cmr)

(二)单位根检验

因为Ng−Perron检验的统计量更为稳健，能较好地避免水平扭曲，并保持较高的检验功效，我们将采用Ng−Perron检验对所选数据进行单位根检验。该检验也称，结合了GLS退势与M统计量，并给出了MGLS的渐近分布及相应的渐近临界值。检验主要包含4个统计量、、、，前两个统计量是经GLS退势后的PP检验统计量和Z的修正统计量，是一个非负统计量，为修正的可行点最优检验统计量。表1显示长期利率原始序列的4个统计量在1%的水平上拒绝原假设，短期利率原始序列的4个统计量在10%的水平上拒绝原假设。因此长、短期利率序列都可认定为(0)或(1)过程。

Perron[21]提出适用于内生性结构突变的单位根检验，其原理是在结构突变未知的条件下，先用结构突变变量的时间趋势项退势，然后用退势的序列进行ADF检验。由于Ng-Perron检验显示序列非平稳，故我们采用该方法判断时间序列是具有结构突变的平稳过程还是具有结构突变的单位根过程。表2的结果显示，长期利率和短期利率的检验值都大于临界值，故原序列是具有结构突变的单位根过程。其中，长期利率的变点时间为2004年11月，短期利率的变点时间为2008年10月，如图2、图3所示。因此，认定长期利率和短期利率序列为(1)过程。

(三)多结构变点检验

由于在利率期限结构分析中所采用的数据往往跨期较大，因此多结构变点出现的可能性更高，根据图1中的数据走势来看，将多结构变点引入协整分析中是合理且必要的。

在多结构变点检验中，设微调值为15%，变点最大值为5，并允许公式(7)中截距和斜率改变。表3显示了各项变点检验的结果和所选出的变点数量和时间。在双最大值检验中，统计量和统计量在1%的水平上显著，并支持模型存在5个结构变点。在Sup Wald检验中，统计量在1%的水平上支持模型存在2~5个变点。序贯检验认为不存在变点；统计量显著性检验认为存在4个变点；信息准则检验认为模型存在3或4个变点。综上所述，判断模型存在4个结构变点是合理的。表3显示，4个变点分别发生在2004年2月、2006年2月、2008年9月和2012年8月。

(四) 协整回归估计

在确定了结构变点后，整个样本区间被分成了5个时段。由于样本数目较少，我们将利用动态最小二乘法(DOLS)来分析和之间是否存在长期均衡的协整关系。该方法由Shin[23]、Saikkonen[24]、Stock和Watson[25]提出，可有效修正解释变量的内生性和OLS估计的误差项。令检验的原假设为协整回归的残差中存在持续性单位根。本文首先建立一个包括所有解释变量的超前项和滞后项的长期动态方程，即DOLS回归模型，如下：

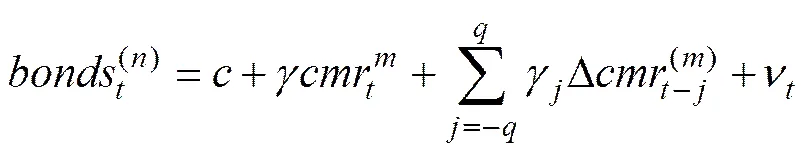
其中：代表存在结构变点的(1)变量的数目(包括截距项)。

表1 Ng−Perron单位根检验

注：1.*、**、***分别表示在10%、5%和1%的水平上显著；

2. 本检验使用了改进的AIC方法，又称MAIC信息准则，主要是用来选取自回归的截断滞后项。临界值由Ng和Perron[21]提供

表2 Perron单结构变点单位根检验

注：1. *、**、***分别表示在10%、5%和1%的水平上显著；

2. 本检验主要利用t统计值进行检验，临界值由Perron[22]提供

通过计算基于DOLS残差的统计量来确定是否存在协整关系。参数即为长、短期利率之间的长期均衡协整系数。

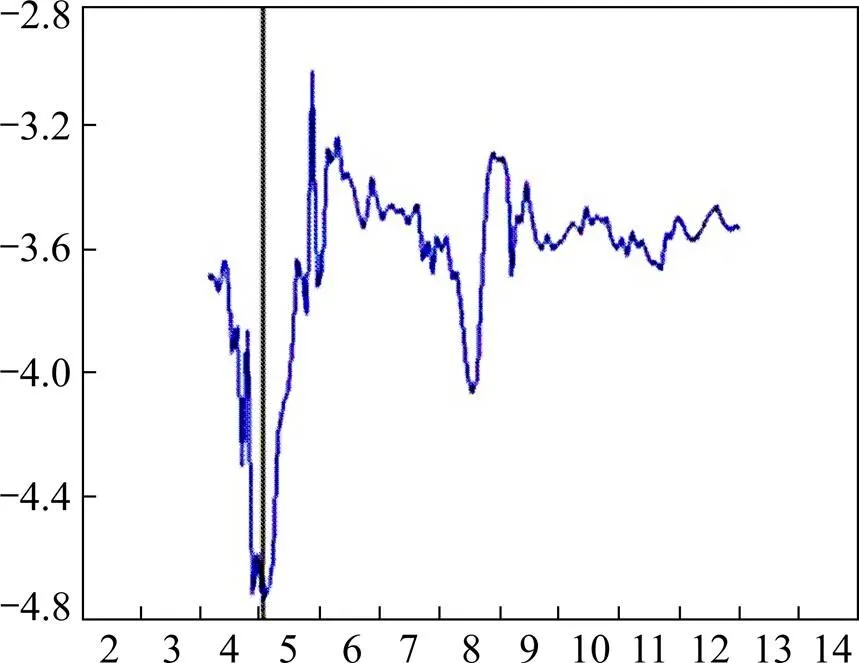
图2 Perron单位根检验(bonds)

将数据按各时段进行协整回归，获得多结构变点模型的协整估计值(见表4)。当模型不存在结构变点时，的值为0.280，对因变量的解释能力很差。在引入多结构变点之后，的值有所上升，在不同时期内基本在1%的水平上显著，因此可以认定模型是存在结构变点的。根据Wald检验结果来看(表4中的W项)，明显不等于1，这不符合预期理论中=1的理论推断。由于在不同时段变化较大，其符号时正时负，其数值时大时小，可以认为，随着短期利率的变化，长期利率有时进行负向调整，有时会产生过度调整，有时则调整不足。我们对表3和表4的结果进行进一步分析。

表3 多结构变化检验

注：1.*、**、***分别表示在10%、5%和1%的水平上显著；

2.代表被解释变量，代表回归量，代表存在变点的(1)变量的数目(包括截距项)，代表(0)变量的个数，代表允许的变点数目最大值；

3. 以95%的置信区间为标准

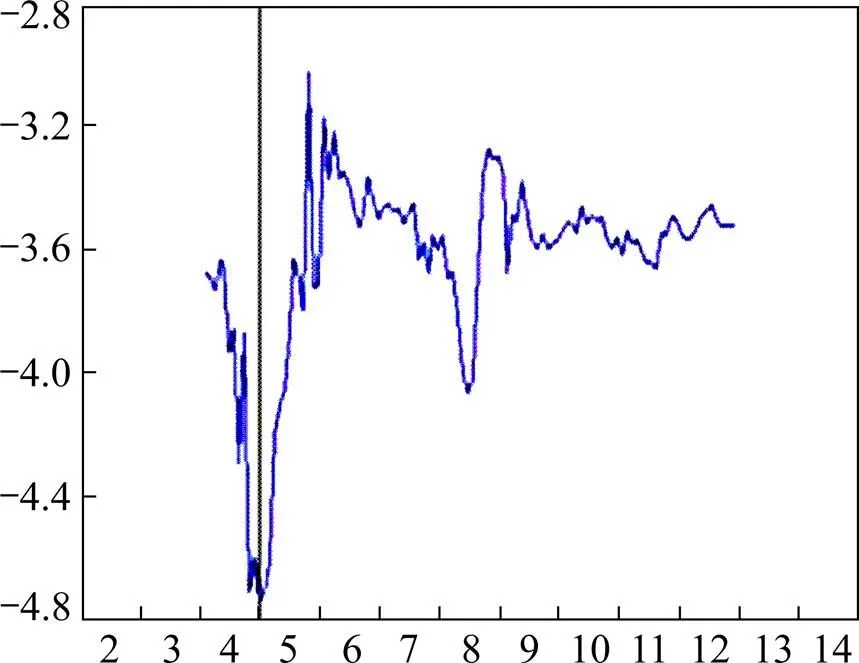
图3 Perron单位根检验(cmr)

1. 协整关系分析

在协整回归模型引入多结构变点后，中国的长、短期利率之间存在着协整关系，但是这一关系存在不稳定性，因此预期理论仅局部成立。在关于协整关系的结果中，有三点值得关注。

(1)协整系数的偏离度。在2012年7月之前，值或很大(绝对值大于1，例如2004年2月至2006年1月)，或很小(绝对值小于0.5，例如2008年9月至2012年6月)。在全球金融危机之前，长、短期利率之间存在反应过度，而全球金融危机则使二者之间的传导效应迅速减少，长期利率对短期利率不再敏感。这一现实与理论的偏离很可能是受到利率、汇率制度改革、通货膨胀以及全球金融危机等多重冲击的影响。预期理论要求利率市场具有完全的自由性，而中国的利率市场化改革在2002年之前进展缓慢。利率、汇率制度尚未实现完全市场化，致使长、短期利率之间的协整关系难以稳定在(1，−1)上。而受全球金融危机的影响，金融市场陷入低迷与混乱之中，导致利率之间的传导效应在之后几年内迅速变小。此后，随着经济的恢复和利率市场化的推进，长、短期利率之间的协整系数上升为0.614，与美国等发达国家的系数更为接近，这说明中国的利率市场化取得了较好的成效。一般认为，反应过度主要是因为政府对利率控制过严，而反应不足则是受利率市场化与经济开放程度的影响。从目前来看，长、短期利率的协整向量仍与理论值有一定差距，长期利率对短期利率的敏感性不够。

(2)协整系数的显著性。由表4可知，当使用全样本进行协整估计时，较小，协整关系的整体显著性不明显。引入多结构变点后，明显增大，协整方程整体显著。但是，在金融危机之后，有所下降，这充分说明类似金融危机这样的外部冲击对长、短期利率的协整关系有十分重大的影响。同时，各时期的都非常显著，说明短期利率对长期利率确实有显著影响。

(3)协整系数的符号变化。在2004年2月至2006年1月、2008年9月至2012年5月以及2012年7月至2014年12月的三个区间内，的符号一直为正号，即长期利率的变化与短期利率预期的变化方向一致，这是符合预期理论的。但是在2002年1月至2004年1月、2006年2月至2008年8月，的符号变成了负号，短期利率上升，长期利率反而下降，长、短期利率之间的反向变化反映出央行上调利率对短期利率引导较好、对长期利率影响较小这一事实。事实上，这一反常现象在美国也有出现。自2004年至2005年，美国联邦基金利率不断上升，同期的10年期国债收益率反而下降，针对这一现象，Bernanke[26]认为是全球经济失衡，尤其是国际储蓄过剩导致长期利率下降。随后一些学者的研究发现，央行的利率政策只能对短期利率产生有效的引导，对长期利率的影响较低。

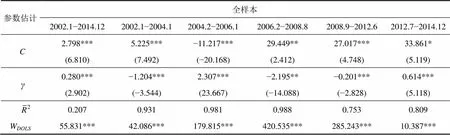
表4 bonds与cmr的协整方程

注：1.*、**、***分别表示在10%、5%和1%的水平上显著；

2. 括号内为t检验值

2. 结构变点成因分析

接下来我们对四个结构变点出现的原因进行分析。从图1中可以发现，2004年2月后，长、短期利差扩大，长期利率出现了一次显著且持续到年末的上升，而短期利率的升幅小，且持续时间短。是什么原因导致了这样的结构变化呢？结合当时的宏观经济发展历程，我们不难发现，结构变点发生在2004年2月，很可能是由于央行上调人民币存贷款利率及进行利率市场化改革，扩大金融机构贷款利率浮动区间所致。一方面，上调利率对于短期市场利率影响不大，拉开了长、短期利差[27]；另一方面，扩大区间打破了利率限制，导致长、短期利率波动范围变大[28]。

2006年2月后，长、短期利率一致呈上升趋势，且利差缩小。这应当是因为央行在2006年至2008年6月多次上调人民币存贷款利率，并且前一时期的利率市场化改革的成效开始显现，央行对货币市场的控制能力增强。

2008年9月后，由于全球金融危机的冲击[29]，长、短期利率出现了较大的背离。背离的具体原因有三：第一，由于实体经济下行压力明显，央行需要下调利率以刺激内需，而与长期市场利率相比，短期市场利率往往对宏观经济更为敏感，因此在这一次的冲击中，长、短期利差再次扩大。第二，汇率波动通过央行冲销操作加剧了资产价格的波动，从而影响利率稳定。第三，债权型货币错配在短期中也会阻碍利率政策绩效的发挥，从而扩大了利差[30]。

2012年7月后，长、短期利差有所缩小，这是由于利率市场化改革又迈出了重要的一步：继2004年放开贷款利率上限和存款利率下限后，央行于2012年6月扩大存款利率浮动区间[31]。随着利率市场化程度提高，长、短期利率之间的协整关系会趋于稳定，利差的波动性也会变小。

四、结论与启示

本文采用多结构变点法和DOLS协整回归模型研究了我国的利率期限结构数据，以此检验预期理论是否在中国成立。实证结果表明：在引入结构变点后，长、短期利率之间存在协整关系，但是这一关系不稳定，因此预期理论仅局部成立。长、短期利率存在协整关系说明央行可以通过调节短期利率来影响长期利率，进而调控实体经济，实现货币政策目标。从整体来看，通过利率调控实现物价稳定等货币政策目标的必要条件已经具备。通过多结构变点检验，我们发现中国的利率结构变点日期分别为2004年2月、2006年2月、2008年9月、2012年7月。在2008年以前，短期利率对长期利率的传导存在反应过度；在全球金融危机发生以后，传导效应迅速变小；2012年7月以后，传导效应上升并趋向理论值。随着时间推移，长、短期利率之间的协整关系逐渐靠近理论值(1，−1)，说明利率市场化效果显著。2015年，存款利率上限全面放开，基本实现利率市场化，央行从直接管制的基准利率向间接引导的基准利率转型，从而在利率市场建立起真正有效的价格机制。在此基础上，利率的价格信号功能得到更有效的发挥，从而助推经济结构升级。

基于上述研究，我们可以得到如下启示。

(一)强化以利率为主的价格型市场化调控

我国目前的货币政策是以货币供应量为中介目标，结合存贷款基准利率对市场进行调整。然而，随着金融创新不断加快、金融市场不断完善，货币供应量的可控性、可测性程度在迅速降低。利率市场化的推进为以利率为主的价格型市场化货币政策调控机制提供了条件，我国的货币政策应当逐渐减少以货币供应量为主的数量型行政性调控，增加以利率为主的价格型市场化调控。

(二)完善国债发行期限结构，增强债券市场的流动性

第一，财政部门应在保证满足政府赤字融资和控制成本的前提下，同时考虑央行公开市场操作对国债的需求，合理安排国债发行的期限结构、频率和数量，提高国债市场的流动性，完善国债收益率曲线，发挥其基准作用，进而增强国债收益率曲线在货币政策传导中的作用。第二，推进银行参与国债期货市场的进度，进一步推动利率掉期产品发展，研究开发与通胀指数挂钩的国债产品。最后，为缓解由于准入管制和投资者风格趋同所造成的流动性不足问题，应进一步放松对债券发行市场的准入管制，加快境外投资者入市步伐，增加QFII、RQFII额度，简化审批程序。

(三)充分利用长、短期利差指标

尽管预期理论没有获得完全的经验支持，但是长、短期利差对未来短期利率变化的预测能力是必须肯定的。本文的实证结果显示，长期利率中包含未来短期利率预期的相关信息。与货币供应量增长率相比，长、短期利差在货币政策预期方面的预测性更好，因此在经济周期波动方面的预测性也更好。

(四)加强预期管理

本文对预期理论的检验结果反映出央行的预期管理尚需加强。欧美国家主要通过清晰地界定政策工具、明确地解释政策调整所应具备的条件、以及定期举行议息会议并公布会议纪要等手段进行预期管理，并取得了较好的效果，因此关于欧美利率期限结构的预期理论检验常能通过。人民银行应一方面加强对宏观经济和利率走向的预测，另一方面加强管理公众和市场对利率的预期，从而有效引导市场预期，提高货币政策效率。

参考文献：

[1] 孙皓, 石柱鲜. 中国的货币政策与利率期限结构: 基于宏观——金融模型的研究途径[J]. 经济科学, 2011, 181(1): 49−59.

[2] 顾亚露, 朱振, 闫妍. 利率期限结构与宏观经济[J]. 中国金融, 2014, 777(3): 87.

[3] 王志强, 李青川, 贺畅达. 利率期限结构与经济增长的非线性关系研究——基于平滑转换模型的实证分析[J]. 金融理论与政策, 2014, 324(4): 27−38.

[4] Campbell J Y, Shiller R. Cointegration and tests of present value models [J]. Journal of Political Economy, 1987, 95(5): 1062− 1088.

[5] Sarno L,Thornton D L, Valente G. The empirical failure of the expectations hypothesis of the term structure of bond yields [J]. Journal of Financial and Quantitative Analysis, 2007, 42(1): 81− 100.

[6] Esteve V. A note on nonlinear dynamics in the Spanish term structure of interest rates [J]. International Review of Economics and Finance, 2006, 15(3): 316−323.

[7] Camarero M, Tamarit C. Instability tests in cointegration relationships: An application to the term structure of interest rates [J]. Economic Modeling, 2002, 19(5): 783−799.

[8] Bai J, Perron P. Estimating and testing linear models with multiple structural changes [J]. Econometrica, 1998, 66(1): 47− 78.

[9] Suardi S. Nonstationarity, cointegration and structural breaks in the Australian term structure of interest rates [J]. Applied Economics, 2010, 42(22): 2865−2879.

[10] Esteve V, Navarro-Ibáñez M, Prats A M. The Spanish term structure of interest rates revisited: Cointegration with multiple structural breaks, 1974-2010 [J]. International Review of Economics & Finance, 2013, 25(1): 24−34.

[11] 吴丹, 谢赤. 中国银行间国债利率期限结构的预期理论检验[J]. 管理学报, 2005, 2(5): 536−541.

[12] 李宏瑾. 基于协整理论的利率期限结构预期理论检验[J]. 投资研究, 2012, 340(6): 52−64.

[13] 李宏瑾. 利率期限结构的远期利率预测作用——经期限溢价修正的预期理论检验[J]. 金融研究, 2012, 286(8): 97−110.

[14] 张雪莹, 陆红, 汪冰. 短期利率与长期利率的关系之谜: 国际表现与中国实证[J]. 上海金融, 2010, 362(9): 144−158.

[15] 王志强, 熊海芳. 结构变点、时变期限溢价与预期理论——来自国内银行同业拆借利率的证据[J]. 数量经济技术经济研究, 2012, 29(5): 104−120.

[16] Taylor M P. Modeling the yield curve [J]. The Economic Journal, 1992, 102(412): 524−537.

[17] Bekaert G, Hodrick R J. Expectations hypotheses tests [J]. Journal of Finance, 2001, 56(4): 1357−1394.

[18] Bai J, Perron P. Computation and analysis of multiple structural change models [J]. Journal of Applied Econometrics, 2003, 18(1): 1−22.

[19] Kejriwal M, Perron P. The Limit distribution of the estimates in cointegrated regression models with multiple structural changes [J]. Journal of Econometrics, 2008, 146(1): 59−73.

[20] Yao Y C. Estimating the number of change-points via Schwarz’ criterion [J]. Statistics & Probability Letters, 1988, 6(3):181−189.

[21] Ng S, Perron P. Lag length selection and the construction of unitroot tests with good size and power [J]. Econometrica, 2001, 69(6): 1529−1554.

[22] Perron P. Further evidence on breaking trend functions in macroeconomic variables [J]. Journal of Econometrics, 1997, 80(2): 355−385.

[23] Shin Y. A residual-based test of the null of cointegration against the alternative of no cointegration [J]. Econometric Theory, 1994, 10(1): 91−115.

[24] Saikkonen P. Asymptotically efficient estimation of cointegration regressions [J]. Econometric Theory, 1991, 7(1): 1−21.

[25] Stock J H, Watson M W. A simple estimator of cointegrating vectors in higher order integrated systems[J]. Econometrica, 1993, 61(4):783−820.

[26] Bernanke B S. Global imbalances: Recent developments and prospects [R]. Berlin: Bundesbank Lecture, 2007.

[27] 滑冬玲. 我国利率政策效果欠佳的制度探究——以2004—2008年利率上调为例[J]. 经济管理, 2008, 449(17): 22−25.

[28] 孙刚, 毛向乾. 金融发展环境、利率市场化与债务融资决策[J]. 广东金融学院学报, 2010, 126(4): 36−48.

[29] 蒋涌. 金融危机冲击下的中国国债利率期限结构分析[J]. 国际经贸探索, 2009, 25(8): 47−52.

[30] 苏应蓉, 李楠. 汇率波动对利率政策经济绩效的影响机理分析[J]. 宏观经济研究, 2014, 183(2): 45−52, 80.

[31] 金中夏, 洪浩, 李宏瑾. 利率市场化对货币政策有效性和经济结构调整的影响[J]. 经济研究, 2013, 545(4): 69−82.

桂林人，武汉大学经济与管理学院硕士研究生，主要研究方向：金融市场

[编辑: 谭晓萍]

Mutation effect of term structure of interest rate: Analysis of cointegration based on multiple structural breaks

HAN Guowen, DENG Yingting

(School of Economics and Management, Wuhan University, Wuhan 430072, China)

Based on expectation hypothesis, the present essay adopts a linear cointegration regression model of multiple structural breaks to study the term structure of interest rates in China. By investigating the cointegration relationship between long-term interest rates and short-term interest rates from January 2002 to December 2014, and by testing dynamic OLS cointegration, we find that on the condition of mutiple structural breaks, there exists a long cointegration relationship between the long and short run Chinese interest rates, and that there is a gap between calculated conintegration vector and theorectical value, which indicates that the results only support a weak version of the expectation hypothesis. Test on multiple structural breaks shows that in sample period, the term structure of interest rates has four break points, and that the sign of coefficients appears reversal repeatedly. Analysis finds that the existence of structural breaks is mainly due to macroeconomic trends, the reform of interest rate and exchange rate, and the 2008 global financial crisis.

term structure of interest rates; multiple structural breaks; expectation hypothesis; Dynamic Ordinary Least Squares

F830.9

A

1672-3104(2016)05−0101−08

2016−04−02；

2016−08−29

国家自然科学基金“中国利率、汇率与央行资产负债及货币供应之间的交互影响：实证分析与政策内涵”(71373187)

韩国文(1968−)，男，甘肃庆阳人，博士，武汉大学经济与管理学院金融系教授，主要研究方向：金融市场；邓颖婷(1991−)，女，广西