路边坡疲劳稳定性分析及其数值计算——基于交通荷载作用

彭　军

(福建省水文地质工程地质勘察研究院　福建漳州　363000)



路边坡疲劳稳定性分析及其数值计算
——基于交通荷载作用

彭军

(福建省水文地质工程地质勘察研究院福建漳州363000)

公路、铁路边坡在不规则动荷载反复作用下会产生疲劳损伤或疲劳破坏。基此，从疲劳分析理论入手，区分材料疲劳与结构疲劳的不同，将边坡视为结构物，结合边坡稳定性分析和边坡疲劳寿命分析方法，提出了边坡疲劳稳定性分析方法。该分析方法与一般的静力稳定性分析的区别在于对疲劳效应的考虑，引入了强度折减技术，建立了“岩土参数—安全系数—疲劳寿命”关系，使安全系数有了与之对应的疲劳寿命。

边坡；动荷载；疲劳寿命；疲劳稳定性

E-mail:1447646950@qq.com

0　引言

自德国的矿业工程师W.A.J.Albert于1829年提出第一份疲劳研究报告以来，人们对疲劳问题的研究已经持续了近两个世纪[1]。但因为当时材料的工作应力很低，结构因疲劳而破坏的事件较少,因此疲劳问题并没有得到足够的重视。20世纪70 年代以后，随着越来越多的结构和构件开始在高应力的状态下工作，疲劳破坏以及疲劳劣化产生的安全度降低问题日益引起了广泛的重视[2]。疲劳破坏的应力水平往往远低于材料的屈服极限和强度极限，破坏时往往没有明显的征兆，因而常常会造成灾难性事故和重大损失[3]。对于公路、铁路的路基或边坡，所受到的交通荷载是频率变化、振幅变化且作用历时也在随机改变的不规则动荷载，在动荷载长期反复作用下, 作为路基或边坡的工程岩土体将产生疲劳损伤，从而造成铁路、公路路基产生不均匀沉降及边坡变形失稳[4,5]。交通荷载作用下边坡岩土体的变形与失稳有其特殊性与复杂性，其疲劳损伤破坏机理研究与防治一直是岩土工作者关注的前沿课题之一，然而目前其仍未形成相应的分析体系。基于此，研究交通荷载作用下岩土边坡的疲劳效应及其对边坡稳定性的影响问题具有重要的理论研究意义及工程应用价值。

1　疲劳累积损伤及边坡疲劳寿命分析方法

当结构承受静荷载时，只要工作应力小于临界应力就认为其是安全可靠的；但是当结构承受交变应力时，即使应力幅值低于临界应力仍将发生破坏，其原因就在于疲劳[6,7]。交变应力是材料疲劳破坏的外因，内因则是损伤累积。当结构承受高于疲劳极限的应力时，每一循环都将使构件受到损伤，损伤累积到一定程度时将引起疲劳失效。疲劳累积损伤理论可以实现变幅荷载或随机荷载与常幅荷载间的转化，进而得以应用常幅荷载下得到的试验结果，疲劳累积损伤理论如图1所示。

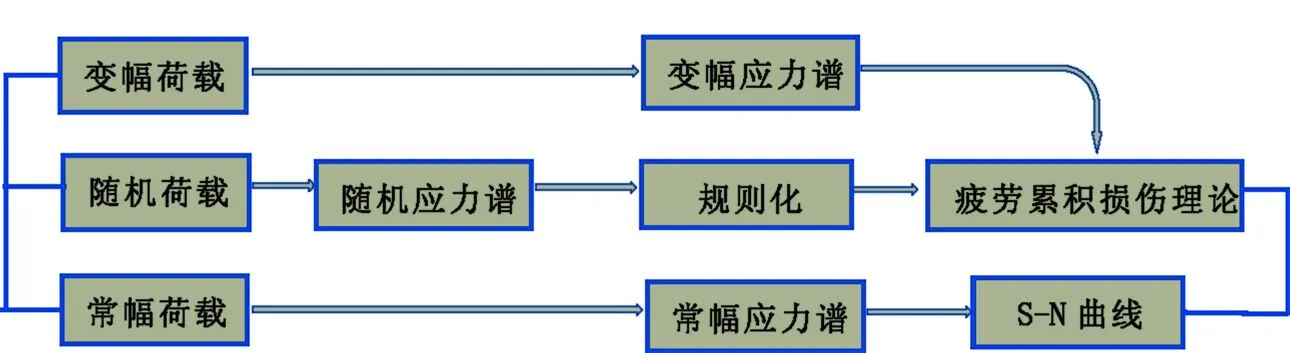
图1　疲劳累积损伤理论的作用

对边坡进行疲劳分析时，为了更好地研究其疲劳破坏的全过程，将其理想化为均质边坡，以边坡出现宏观裂缝为破坏，故该疲劳分析仅涉及疲劳裂纹形成阶段的寿命Ni。该阶段的疲劳法则适合使用S-N曲线(S-N曲线如图2所示)与疲劳累积损伤理论进行疲劳寿命的估算[8]。

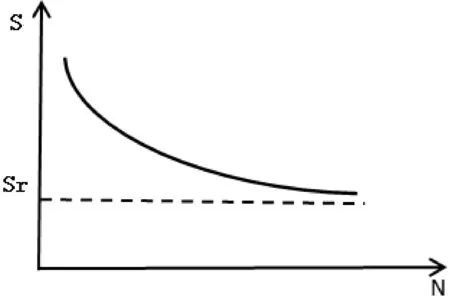
图2　S-N曲线示意图

本文将名义应力法与通用试验-分析法合并细化使其成为适用于分析边坡疲劳寿命的方法。名义应力法的出发点是构件的危险部位(应力集中部位)的名义应力，以名义应力S为参数，以材料或构件的S-N曲线为基础，计入有效应力集中系数、尺寸系数、表面系数和不对称循环系数等因素的影响，适当地结合疲劳累积损伤理论，从而得到危险部位的疲劳寿命[9]。试验-分析法是依据材料的疲劳性能，对照结构所受的载荷历程，对结构做应力-应变分析。结构疲劳分析的试验法完全依赖于试验，它直接通过与实际情况相同或相似的条件对结构做足尺试验以获得疲劳数据。该方法是传统方法，获得的数据真实可靠。故将名义应力法与通用试验-分析法结合起来对边坡做疲劳寿命分析。

2　边坡疲劳稳定性分析

考虑疲劳效应的边坡稳定性分析即称边坡疲劳稳定性分析。边坡疲劳稳定性分析与一般的边坡稳定性分析既有联系又有区别。目前，边坡静力稳定性分析的方法主要可以分为以下几类：确定性分析方法、不确定性分析方法、数值模拟法和综合评价方法[10]。边坡动力稳定性分析常采用的方法有：拟静力法、Newmark滑块位移法、概率分析法及数值模拟法。边坡岩土体在受到诸如交通荷载此类交变荷载的长期反复作用将产生疲劳效应。交通荷载属于动荷载范畴，但其疲劳效应对边坡稳定性产生的影响明显，非前述一般的动力稳定性分析方法所能描述，其重要差别在于是否考虑交通荷载对岩土边坡的长期影响。该长期影响又集中地体现在边坡疲劳寿命上，如何建立边坡稳定性与边坡疲劳寿命的联系就成了解决上述问题的关键。

近年来，随着强度折减法的提出与成功应用，运用有限元分析方法求取岩土边坡安全系数方面取得了重大进展[11]。对于强度折减法，Duncan 曾指出边坡的安全系数可以定义为：对岩土的剪切强度进行折减的程度应使得边坡刚好达到临界破坏状态,即定义安全系数是岩土的实际抗剪强度与临界破坏时折减后的剪切强度的比值。这种强度折减技术特别适用有限元方法来实现[12]。在有限元稳态计算中，如果模型为不稳定状态，有限元计算将不收敛。基于此原理，在非线性有限元边坡稳定分析中，通过降低岩土体的实际强度参数，将粘聚力c与内摩擦角φ值同时除以一个折减系数Fsr，得到一组折减后新的c′、φ′值，即：

(1)

(2)

然后将折减后的c′、φ′值作为新的材料参数代入有限元计算方程中进行试算。若有限元计算收敛，则表明边坡仍处于稳定状态,对折减系数Fsr取稍大一些后再代入试算，直到有限元计算不收敛达到不稳定状态时为止。当由于强度参数的折减而造成有限元计算不收敛时，说明此时岩土体达到临界极限状态，边坡发生剪切破坏。此时采用的折减系数Fsr即为该边坡的稳定安全系数，此时的滑移面即为实际滑移面。

对于 Drucker-Prager 屈服准则使用强度折减法计算边坡安全系数时，令安全系数为Fsr，则该准则可写为：

(3)

有限元强度折减法综合了有限元法、弹塑性分析法和强度折减技术的优点，不仅能够较真实地考虑边坡岩体的非均质、不连续和非线性特性；避免了将坡体视为刚性块体而过于简化计算边界条件的缺点，而且能够较接近实际情况地从应力-应变方面入手分析边坡的变形破坏机制，在计算边坡应力、位移、塑性区的基础上，直接得到边坡的破坏面特征；求解边坡的安全系数时，无需事先假定滑移面的形状和位置，也无需对滑体进行条分，使边坡问题的求解变得更加简单。至此，采用共同的边坡有限元结构分析方法便将边坡稳定性分析与边坡疲劳寿命分析联结在一起；再借助于强度折减分析方法，即可建立“岩土参数-安全系数-疲劳寿命”三者联系。于是，以往所熟知的边坡稳定安全系数不再是一成不变的了，而是有了与之对应的疲劳寿命，将随着疲劳寿命的消耗而逐渐衰减。针对主要受交通荷载控制的边坡而言，其疲劳稳定性分析基本思路如图3所示。

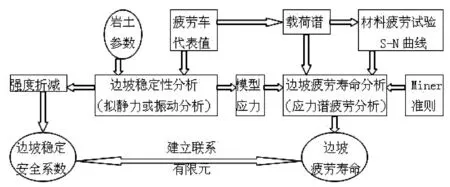
图3　边坡疲劳稳定性分析方法

3　数值计算

以205省道三明沙县段边坡为例对比了静力稳定性分析、动力稳定性分析及疲劳稳定性分析。坡高共20 ，分2级，每级10 ，坡率均为1∶1；中间平台宽10 ，行车道路宽8 ，双向双车道；坡体材料为中风化砂岩。边坡典型剖面如图4所示。

图4　205省道三明沙县段边坡典型剖面图

坡体材料理想为均质中风化砂岩，由进行岩石疲劳试验的同一批岩石试样获取边坡结构分析所需参数，并对边界条件作如下设定：①顶部边界：自由表面；②底部边界：施加水平和竖直方向位移约束；③两侧边界：施加水平方向位移约束。同时将边坡模型简化成平面应变问题，对于平面问题，边坡岩土体的模拟可以选择采用4节点四边形单元或8节点四边形单元，其单元形式如图5、图6所示。

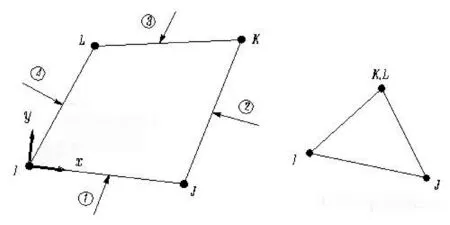
图5　4节点四边形单元及其退化形式

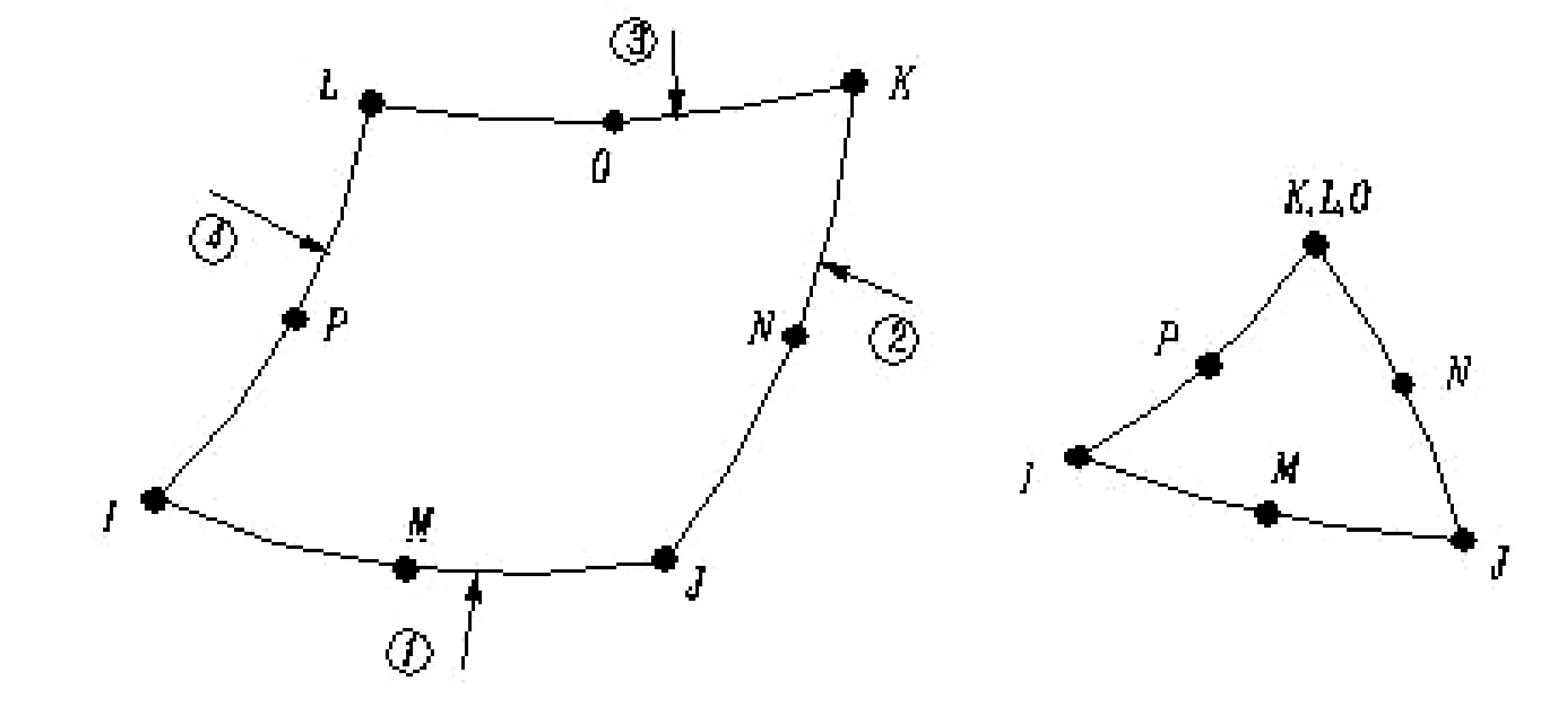
图6　8节点四边形单元及其退化形式

根据均质边坡的特点，在反复对比划分尺寸对计算结果精度与耗时两方面的影响后，最终确定采用2m为单元尺寸进行网格划分。对边坡做静力稳定性分析时，仅考虑在坡体自重作用下产生的失稳破坏。对边坡做动力稳定性分析时，需考虑交通荷载对边坡稳定性的影响，实测的车辆荷载如图7、图8所示，建立的边坡有限元计算模型如图9所示。

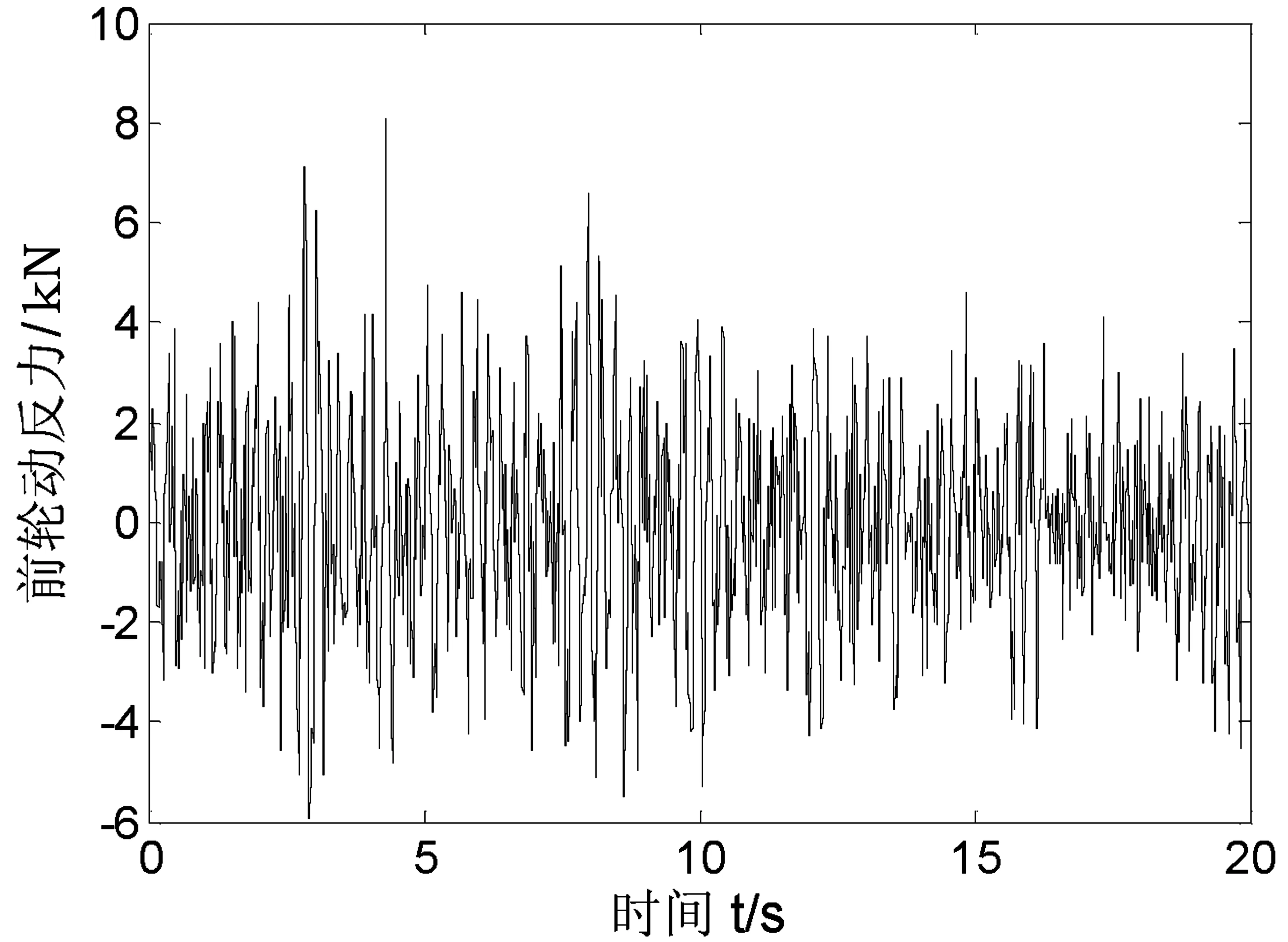
图7　车辆前轮动反力时程曲线

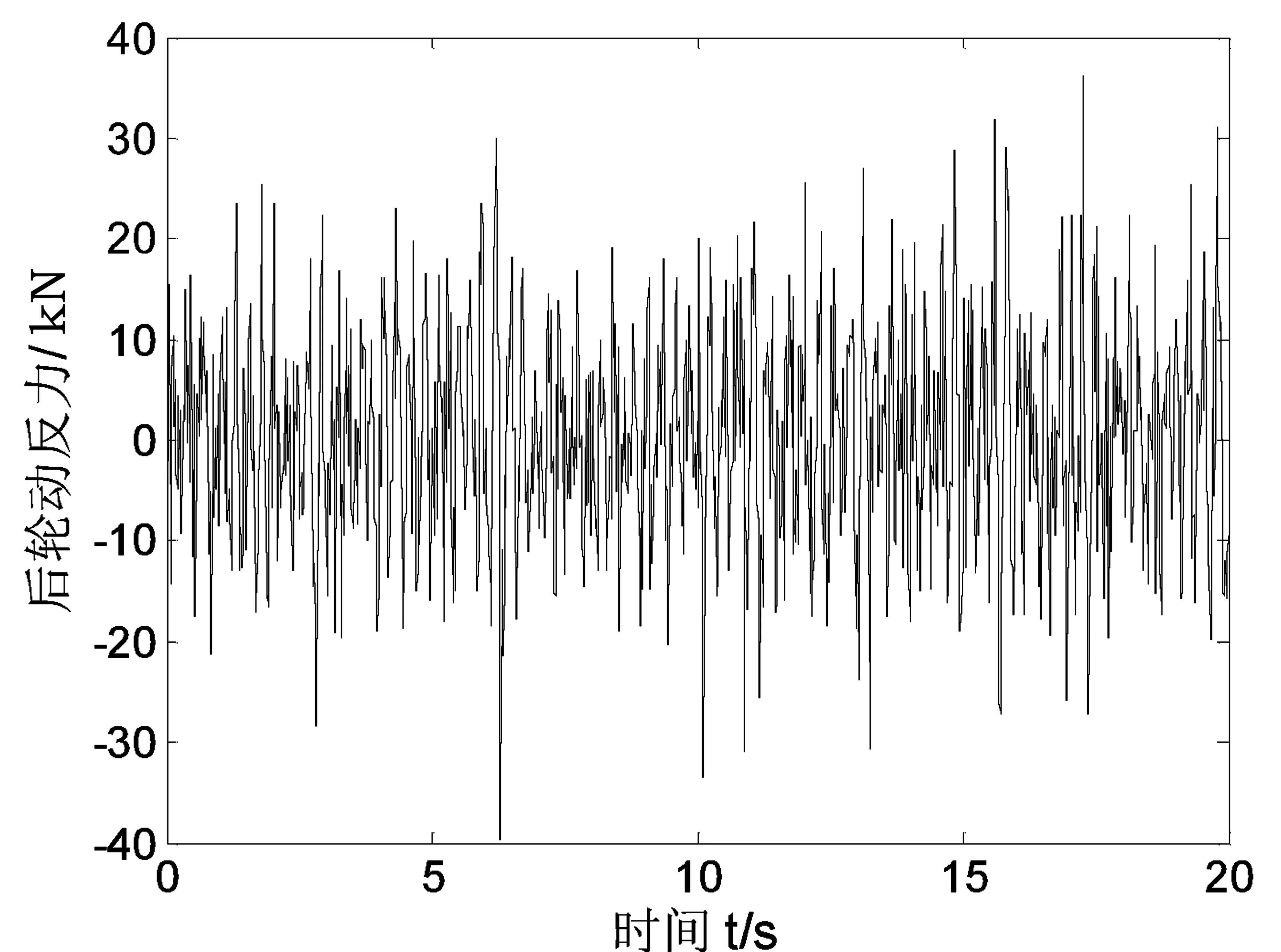
图8　车辆后轮动反力时程曲线

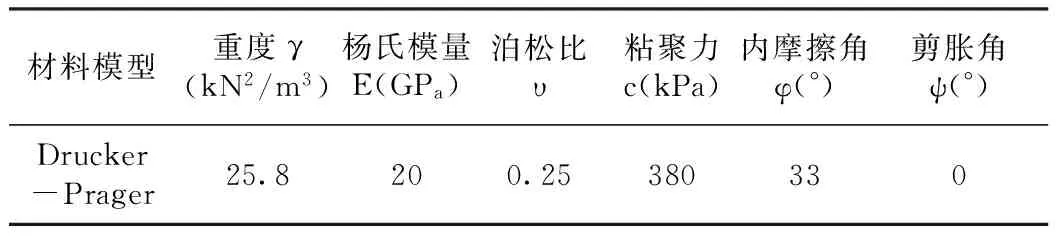
材料模型重度γ(kN2/m3)杨氏模量E(GPa)泊松比υ粘聚力c(kPa)内摩擦角φ(°)剪胀角ψ(°)Drucker-Prager25.8200.25380330

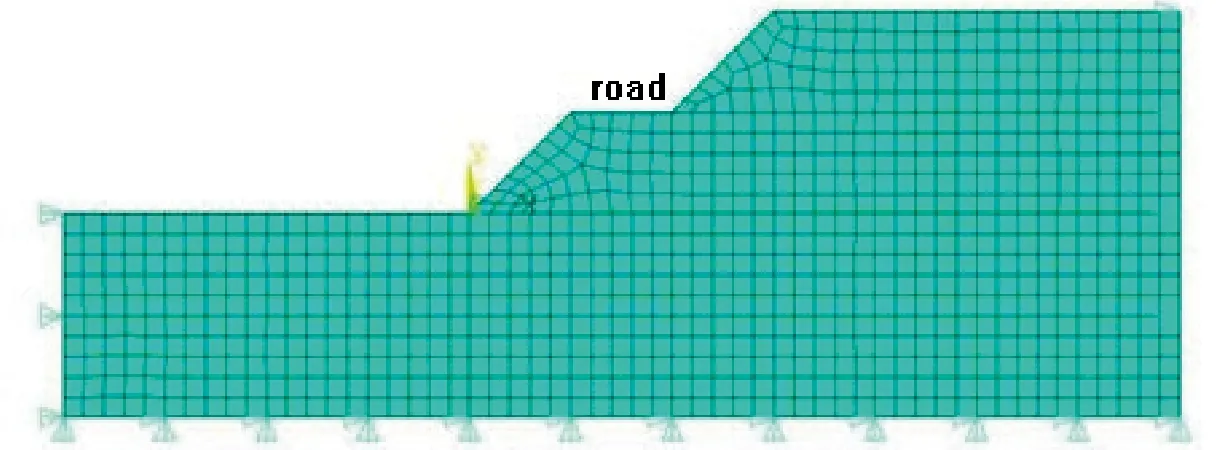
图9　边坡有限元计算模型

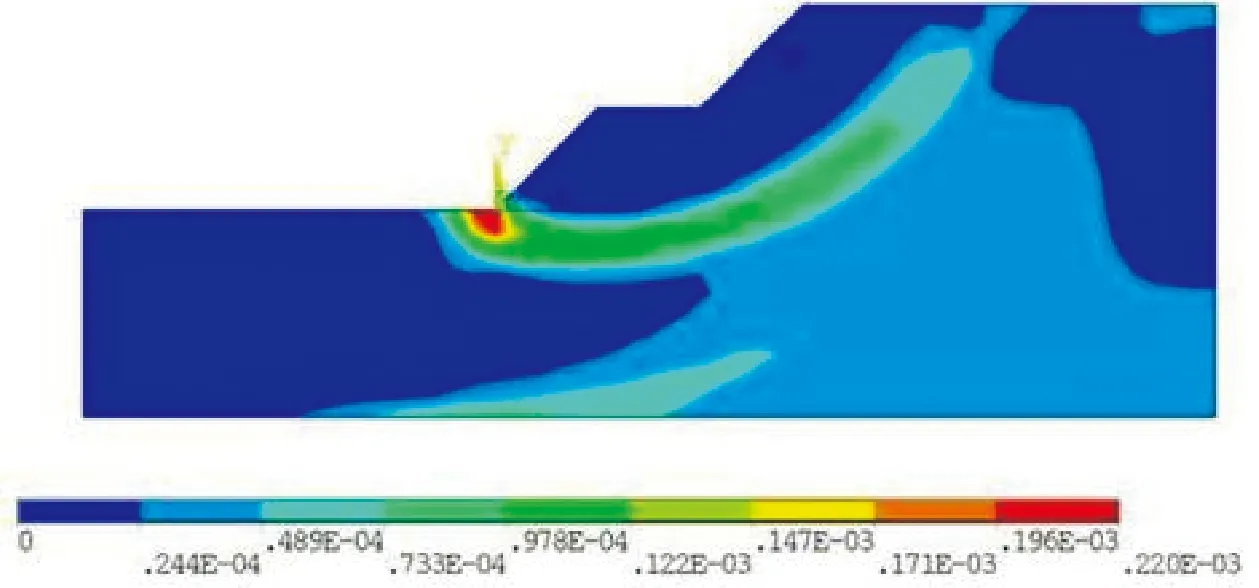
图10　静力稳定性分析方法Von Mises塑性应变图

从图10不难看出，按《公 路 路 基 设 计 规 范》(JTG D30-2015)(下简称《规划》)中(3.6.9-1)，在不考虑交通荷载作用的情况下，边坡潜在破坏面为从坡脚延伸至坡顶，由此计算得到该边坡安全系数Ks=7.92，该值恒定不变。根据规范中给出的安全系数规定，该边坡处于一种非常稳定的状态，并且由于安全系数是恒定的，这种稳定状态将一直保持下去。通过对比图11和图12可以看出，考虑车辆荷载后的边坡破坏形式与不考虑时发生了明显的变化，潜在破坏面变为从坡脚延伸至第一级行车平台。借鉴《规范》中(3.6.9-1)，在考虑车辆荷载作用后计算得该边坡安全系数Kd=7.06，该值要比按静力稳定性分析方法得到的值小10.86%。即便如此，该边坡仍处于一种非常稳定的状态。同样，这种稳定状态也将一直保持下去。从图12中可见边坡的疲劳区域由第一级行车平台逐渐向下扩展至坡体深部，疲劳热点(红色Min所指)出现在第一级行车平台面上，该处所示最小疲劳寿命为1.176×107次。

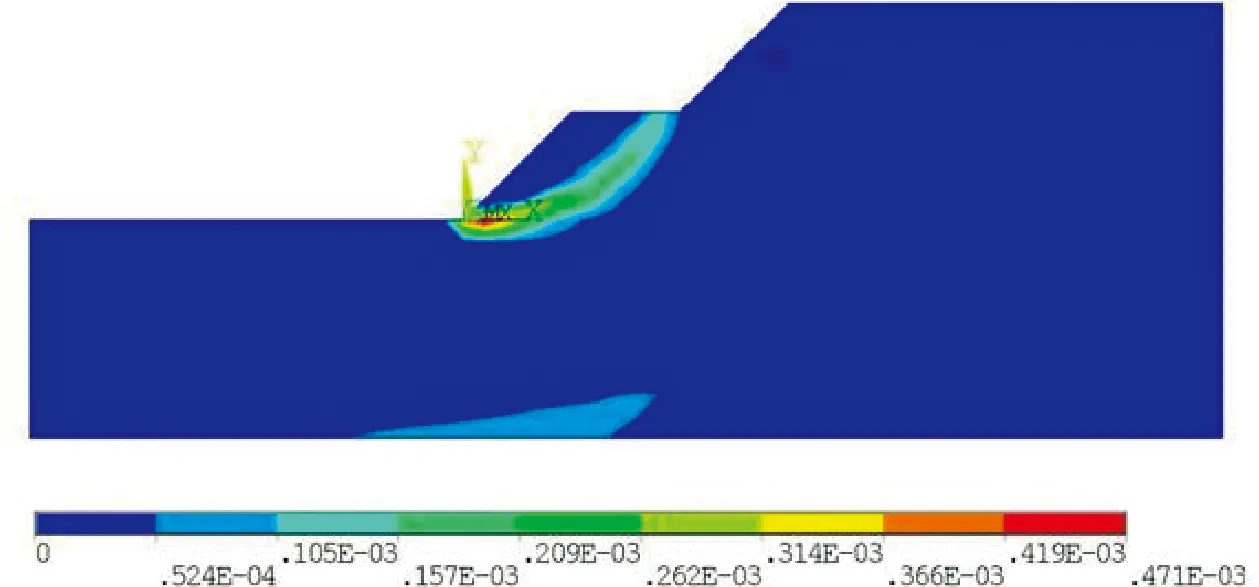
图11　动力稳定性分析方法Von Mises塑性应变图

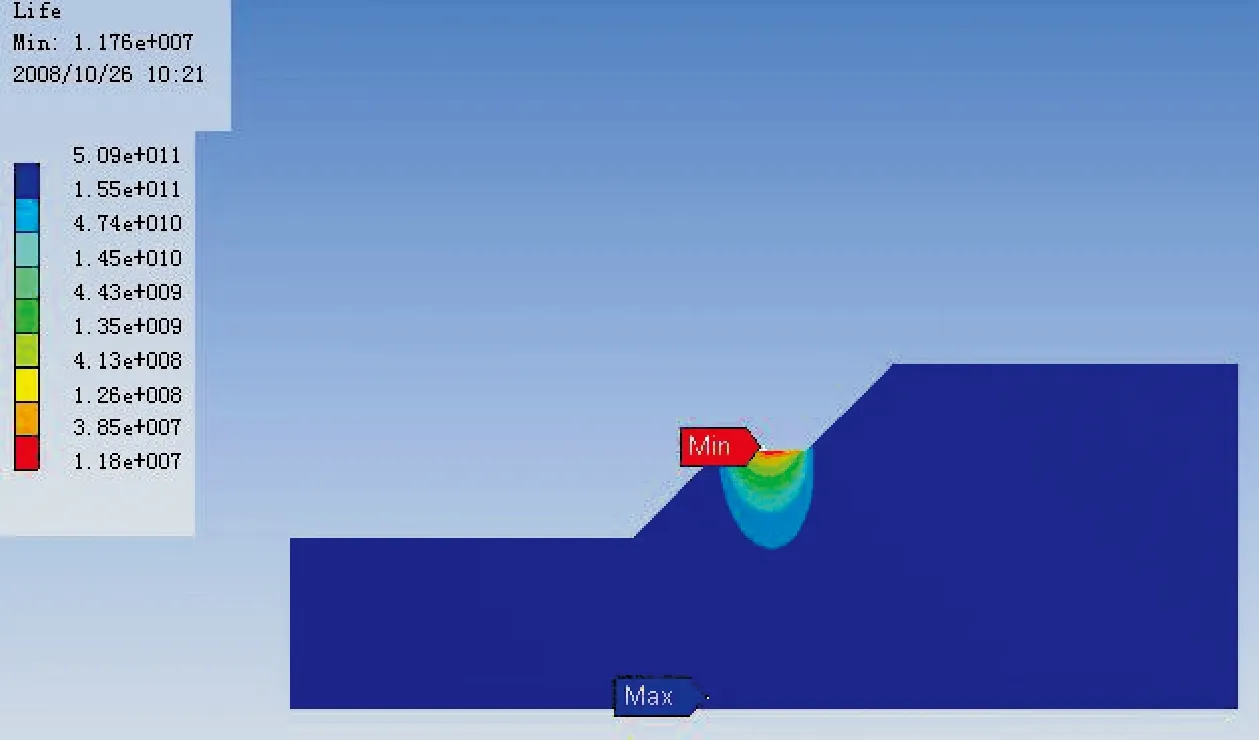
图12　边坡疲劳寿命图

本文用于疲劳寿命估计的方法认为：结构危险部位的疲劳寿命即为结构的疲劳寿命，当危险部位发生疲劳破坏时即认为结构退出工作。故可取第一级行车平台面上的最小疲劳寿命1.176×107次为边坡的疲劳寿命。按照本文提出的边坡疲劳稳定性分析方法，该边坡的安全系数为一逐渐减小的变化值:初始安全系数Kf1=7.63,在经历1.176×107次疲劳荷载循环作用后，以213160次/年计，即在经历了约55年后边坡将有可能发生因疲劳所致的失稳破坏。边坡稳定

性分析得到的安全系数在有了与其对应的疲劳寿命之后，不再是恒定不变的固定值，而是具有一定的时效性。

4　结论

本文从疲劳分析的基本理论入手，指出了对边坡进行疲劳稳定性分析的必要性；并得到下列结论：(1)在获得边坡疲劳寿命分析方法的基础上，进一步使其与边坡稳定性分析建立联系，提出了边坡疲劳稳定性分析方法；(2)边坡疲劳稳定性分析方法指出了边坡疲劳稳定性分析与一般的静力稳定性分析或动力稳定性分析的不同在于对疲劳效应的考虑；(3)引入强度折减技术，建立“岩土参数-安全系数-疲劳寿命”关系，使安全系数有了与之对应的疲劳寿命，说明安全系数并非一成不变，而是具有一定时效性的，将随着疲劳寿命的消耗而逐渐衰减。

[1]孔令伟,陈正汉.特殊土与边坡技术发展综述[J].土木工程学报,2012,45(5):141-161.

[2]郑颖人,赵尚毅,时卫民,等.边坡稳定分析的一些进展[J].地下空间,2001,2(4):262-271.

[3]H.H.Hung and Y.B.Yang.Elastic waves in visco-elastic half-space generated by various vehicle loads[J].Soil Dynamics and Earthquake Engineering, 2001, 21:1-17.

[4]李玉銮.边坡变形及其失稳影响因素分析[J].福建建筑,2006,3:67-69.

[5]秋仁东,石玉成,付长华.高边坡在水平动荷载作用下的动力响应规律研究[J].世界地震工程,2007,23(2):131-138.

[6]陈力华,靳晓光.有限元强度折减法中边坡三种失效判据的适用性研究[J].土木工程学报,2012,45(9):136-146.

[7]李典庆,蒋水华,周创兵,等.考虑参数空间变异性的边坡可靠度分析非侵入式随机有限元法[J].岩土工程学报,2013,35(8):1413-1422.

[8]杜太亮,张永兴,谢强,等.岩体基本参数对岩质边坡变形的影响[J].中国地质灾害与防治学报,2006,17(1):22-27.

[9]程灿宇,罗富荣,戚承志,等.有限元强度折减法计算边坡稳定的对比分析[J].岩土力学,2012,33(11):3472-3478.

[10]Yong-Qiang Zhang, Hong Hao, Yong Lu.Anisotropic Dynamic Damage and Fragmentation of Rock Materials under Explosive Loading.International Journal of Engineering Science, 2003, 41: 917-929.

[11]Bagde, M.N.; Petros, V..Fatigue properties of intact sandstone samples subjected to dynamic uniaxial cyclical loading.International Journal of Rock Mechanics and Mining Sciences, 2005, 42(2): 237-250.

[12]周翠英,刘祚秋,董立国,等.边坡变形破坏过程的大变形有限元分析[J].岩土力学,2003,24(4):644-647.

彭军(1983.7-)，男，副院长，注册岩土工程师，主要从事基坑及边坡稳定性方面的研究。

Fatigue stability analysis and numerical calculation of roadside slope——Based on traffic load

PENGJun

(Institute of Hydrogeological Survey and Engineering Geological Investigation of Fujian Province, Zhangzhou 363000)

The road and railway slope under the action of irregular dynamic load will happen fatigue damage or fatigue failure. Based on the fatigue analysis theory, the difference between the material fatigue and structural fatigue, and regard the slope as the structure, combined with the slope stability analysis and the fatigue life analysis method, the slope stability analysis method is proposed. In order to make the evaluation of the long-term stability of the highway and the railway side slope and avoid all kinds of environmental vibration caused by the rock and soil disaster prevention and control,this method has certain theoretical significance and engineering application value.

Side slope；Dynamic load；Fatigue life；Fatigue stability

彭军(1983.7-)，男，工程师。

2015-11-24

TU435

A

1004-6135(2016)01-0035-04