偏微分方程最优控制中的变分迭代法应用
姜 彬
(南通航运职业技术学院 管理信息系, 江苏 南通 226000)
偏微分方程最优控制中的变分迭代法应用
姜彬
(南通航运职业技术学院 管理信息系, 江苏 南通226000)
首先使用极大值原理得到偏微分方程问题的最优性条件,然后使用变分迭代法求解Hamilton-Pontryagin方程,实现了偏微分方程最优控制问题的准确快速求解。结合两个最优控制的经典实例,对模型和算法进行了仿真实验,证明了该方法的可行性和有效性。
变分迭代法; 偏微分方程; 最优控制; 极大值原理
0 引 言
有很多实际的工业生产过程中的优化模型本质上是偏微分方程的最优控制问题。常微分方程的最优控制问题已经有了较为成熟的求解方法,而偏微分方程的最优控制问题由于计算复杂,偏微分方程往往不存在解析解等困难,在常微分方程里边常见的经典分析方法不能够完全适用[1]。因此,对偏微分方程最优控制问题的研究显得很有意义。
基于常微分方程的最优控制问题已经有了很多有效的方法来进行求解,例如变分法、极大值原理、动态规划[2-4]等。对于偏微分方程的最优控制,文献[5]提出了基于Hamilton-Pontryagin方程的求解方法,文献[6-8]通过导出偏微分方程的对偶方程,给出该类问题的最优性条件。虽然这些方法理论上可以应用,但往往由于数值求解的计算复杂性,使这些方法有很大的局限性。今年以来变分迭代法被广泛地应用到偏微分方程的求解中,文献[9]提出了一种变分迭代方式。文献[10]证明了变分迭代法的解可以收敛于精确解。文献[11]将传统的参数摄动法和变分迭代法相结合,给出了一种改进的变分迭代公式。
文中在全面研究了变分迭代法理论的基础上,从工业生产过程中抽象出一类偏微分方程最优控制问题,先推导出Hamilton-Pontryagin方程,在此基础上采用变分迭代法来求解原偏微分方程和对偶的偏微分方程,并采用了参数的方法来表示偏微分方程的初始解和边界条件。实验表明,该方法能够快速地逼近偏微分方程的真实解,从而简化了计算过程。
1 问题的提出
我们考虑如下的偏微分方程最优控制问题:
(1)
初始条件为:
(2)
边界条件为:
(3)
末端条件为
(4)
在一些问题中,末端条件也可以是自由的,根据所讨论问题不同会有一些小的变化,这里讨论更加一般的问题。
上面偏微分方程最优控制问题中,u(x,t)是控制量,y(x,t)是状态变量,yt(x,t),yx(x,t),yxx(x,t)分别表示状态变量对时间的导数、对空间的一阶导数和二阶导数。r是一个常数,表示对控制量惩罚的大小。α0,α1,β0,β1分别是常数。
对式(1)分析可知,我们希望在t∈[0,T],x∈[0,L]时,状态量y(x,t)能够尽量接近设定值yd,同时对控制量进行一定的惩罚。式(2)和式(3)分别是偏微分方程的初始条件和边界条件。式(4)是终点约束。
根据极大值原理可以得出该最优控制问题最优解的必要条件。由极大值原理分析该问题可得到如下结论:
(5)
式中:p(x,t)——对偶状态,可以由对偶方程得出。
极小化该哈密顿函数,即可得到最优解。
如果假设最优的控制律满足如下的函数表达式:
(6)
那么可知:
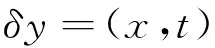
(7)
最优的控制律和对偶状态还满足以下的对偶方程约束:
(8)
边界条件为:
(9)
初始条件为:
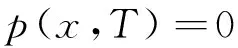
(10)
式(8)的两个偏微分方程,一个是原问题的偏微分方程,另一个是对偶的偏微分方程,可以看到它们很相似,但也有不同对偶方程有着自己的边界条件和初始条件,对偶方程和原方程互相耦合在一起。所以,在求解的时候必须同时求解原方程和对偶方程。因此,要想利用最优性条件求解该问题就必须求解原偏微分方程和对偶的偏微分方程。
2 基于变分迭代法求解偏微分方程最优控制问题
2.1变分迭代法
近年来对变分迭代法的研究很多,该方法被广泛的用来求解偏微分方程取得了很好的效果。我们要使用变分迭代法来求解原偏微分方程和对偶偏微分方程。考虑如下的一个偏微分方程:
(11)
式中:Lt,Lx——微分算子;
N——非线性算子;
f(x,t)——普通的非线性函数。
由此,我们给出如下的变分迭代法的迭代公式:
(12)
上式中等式右边第二项是校正项,λ是拉格朗日乘子,可以由变分理论最佳确定,yk是对微分方程解的第k次迭代时的近似。该方法通过给定一个初始解y0(x,t),然后通过不断的迭代去修正这个初始解来逼近真解。函数y(x,t)的改变量为自变函数的变分,可以用δy(x,t)表示。
如式(12)是常见的变分迭代法的公式,但对于复杂的偏微分方程,该方法往往收敛速度较慢,甚至无法收敛到最优解。文中基于迭代优化的思想提出了双层结构的变分迭代公式。考虑如下偏微分方程:
(13)
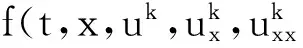
(14)
其中
由此可以得出,迭代表达式为
(15)
同时对其两边求变分,可以得到修正之后的表达式:
(16)
对式(16)两边同时求变分可知
(17)
由此可得拉格朗日乘子的驻值条件
(18)
令初始条件
(19)
由此可知,近似解yk(x,t)能够通过迭代公式完全确定,最后可以确定该偏微分方程的近似解为:
(20)
2.2算法流程
首先要求解原偏微分方程和对偶偏微分方程,即式(8),根据式(16)可以给出如下的迭代表达式:
(21)
(22)
方程的近似解式(17)和式(18)必须验证初始条件、边界条件、横截条件和最终状态条件是否满足。因此,提出了选择这些零的近似作为独立变量的多项式函数z和t,涉及未知参数被强加边界和横截条件。值得注意的是变分迭代法收敛到近似解选择为零的近似,但所需的迭代次数达到这样的精度取决于所选的零级近似[13]。
(23)
迭代次数也与所选最终的终止条件有关,在这里我们选择这样的一个终止条件。
(24)
式中:ε——一个可以自由确定的小数,可根据经验来给定。
由此,给出变分迭代法求解该偏微分方程最优控制问题的算法流程:
1)令k=1,选择初始解y0(x,t)和λx(τ)=λp(τ)=1。
2)依据变分迭代的公式,即式(17)和式(18)来计算出yk(x,t)和pk(x,t)。
3)检验yk(x,t)和pk(x,t)是否满足边界条件和初始条件,若不满足,则返回步骤2)继续修正迭代yk(x,t)和pk(x,t);若满足,则进入下一步。
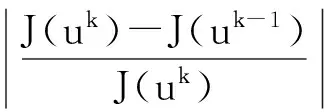
3 应用研究
给出一个具体的偏微分方程最优控制问题,该问题是一个经典的控制问题,我们使用变分迭代法来求解。
考虑如下的最优控制问题:
r[u(x,t)]2dxdt
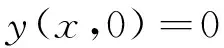
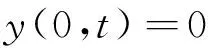
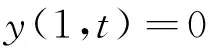
(25)
由此可得,该最优控制的哈密顿函数为:
(26)
由式(26)可知该问题的极值条件为
(27)
由式(27)可知
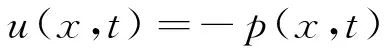
(28)
将式(28)代入式(26)可得
(29)
由对偶方程的表达式可知:
(30)
边界条件为
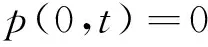
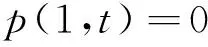
(31)
初始条件为
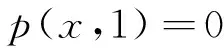
(32)
使用变分迭代法来求解原偏微分方程和对偶偏微分方程,由变分迭代法的公式,即式(21)和式(22)可得:
(33)
(34)
对上式两边同时求变分可得:
(35)
(36)
对上式整理可得:
(37)
(38)
又因为
我们可得
(39)
由此可以得出关于拉格朗日乘子的约束:
(40)
由此可以解出λx(τ)=λp(τ)=1,将上式代入式(33)和式(34)中,可得
(41)
(42)
迭代所求的解必须满足初始条件和边界条件,对偶状态也要满足相应的约束,由此可以对其进行参数化处理。
(43)
经过两次迭代,可以得到如下的结果:
(44)
迭代初始条件和边界条件可得:
(45)
将边界条件代入式(44),由此可以解得参数:
(46)
因此可得其近似解为
(47)
近似的最优控制
(48)
由此计算出适应值函数为:
(49)
之后的迭代过程与前面是一样的过程,下面直接给出第6步迭代的结果,此时已经得到了最优解。
(50)
(51)
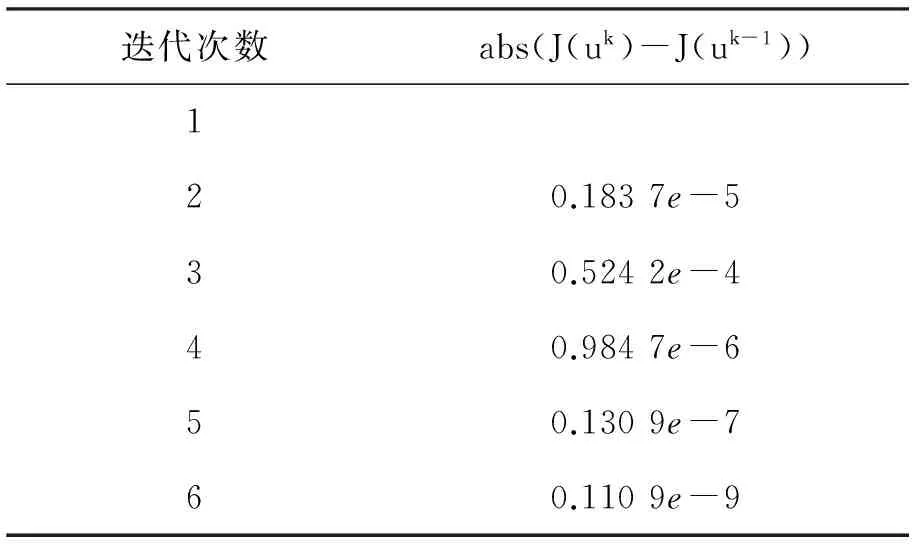
表1 适应值函数迭代变化过程
由表1分析可知,适应值的变化量是在逐步减少的,当小于预先设定值时,该算法终止,即得出最优解。
让我们考虑如下的最优控制问题
(52)
考虑如下约束
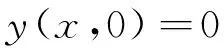
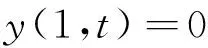
由此可得该问题的哈密顿函数为:
(53)
由此得出状态方程,协态方程和它们的边界条件为:
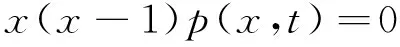
x(x-1)p(x,t)=0
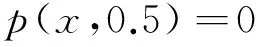
(54)
由此给出迭代的表达式为:
(55)
(56)
同理可知,我们还是要检验该方程是否满足初始条件和边界条件。若该解满足微分方程的初始条件和边界条件,则可以对其进行参数化表示:
(57)
该问题通过变分迭代法迭代5步即得到最优解,适应值函数迭代变化过程见表2。
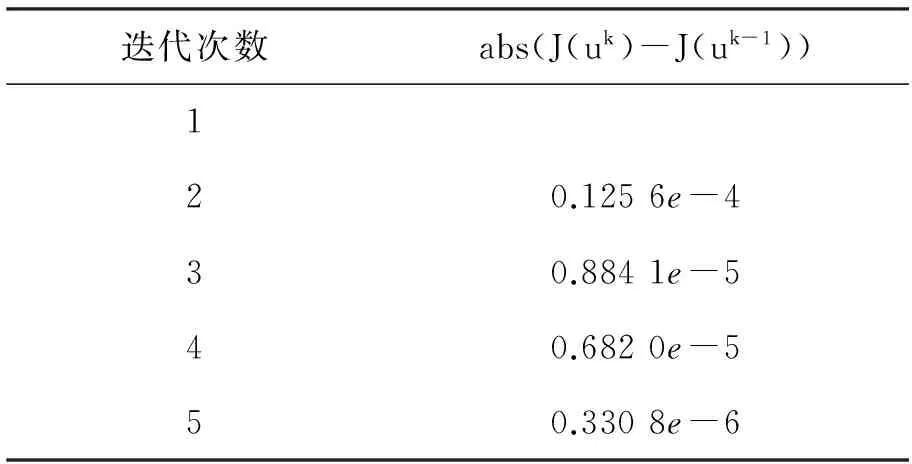
表2 适应值函数迭代变化过程
由表2分析可知,适应值的变化量是在逐步减少的,当小于预先设定值时,该算法终止,即得出最优解。
最优状态量随时间空间的分布如图1所示。
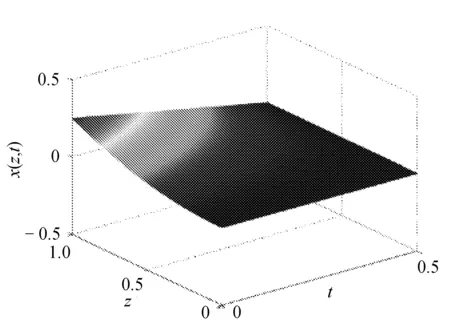
图1 最优状态量变化图
由图1分析可知,最优的状态量能够很好地跟踪我们给出的设定值。
对偶状态量随时间空间的分布如图2所示。
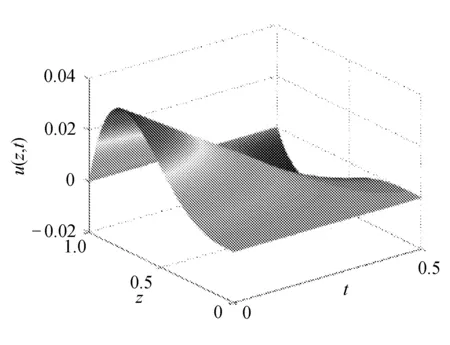
图2 最优对偶状态量变化图
由图2分析可知,最优的对偶状态量能够满足初始条件和边界条件。
最优的控制量随时间和空间的分布如图3所示。
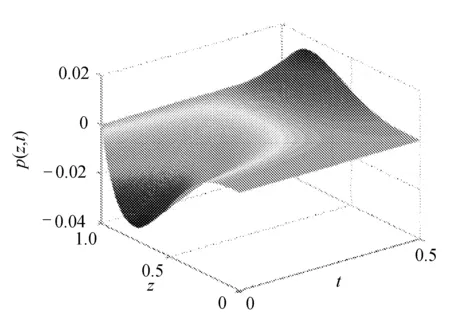
图3 控制量变化图
由图3分析可知,最优的控制量随着时间的增大控制量要相应的增大,来达到最优的控制目标。
4 结 语
采用变分迭代法解决偏微分方程的最优控制问题。先由经典的极大值原理导出该问题的最优性条件,即Hamilton-Pontryagin方程导出最优性条件,然后给出适当的边界和横截性条件。为了求解这些方程,我们使用了全新的变分迭代法进行求解。
采用对近似解析解不断迭代校正的方法来通过多项式函数逼近真实解。并且文中由两个应用实例说明了该方法的有效性。下一步的研究方向是如何改进变分迭代法,使得该方法的收敛速度加快,能够在较快的时间内收敛到真实解。
[1]EugeniuszZieniuk,Dominik.Parametricintegralequationssystemsin2Dtransientheatconductionanalysis[J].InternationalJournalofHeatandMassTransfer,2014,78(12):571-587.
[2]谭拂晓,刘德荣,关新平,等.基于微分对策理论的非线性控制回顾与展望[J].自动化学报,2014,40(1):1-15.
[3]HYe,FLiu,VAnh,etal.Maximumprincipleandnumericalmethodforthemulti-termtime-spaceRiesz-Caputofractionaldifferentialequations[J].AppliedMathematicsandComputation,2014,227(15):531-540.
[4]孙勇,张卯瑞,梁晓玲.求解含复杂约束非线性最优控制问题的改进Gauss伪谱法[J].自动化学报,2013,39(5):672-678.
[5]程建锋,董新民,薛建平,等.基于Gauss伪谱法的飞机最优目标瞄准控制[J].计算机应用,2013,33(11):3291-3295.
[6]Penalty.MPQImethodforconstrainedparabolicoptimalcontrolproblems[J].InternationalJournalofComputerScience,2014,2(12):635-648.
[7]刘西林,王泽文,邱淑芳.基于Priwitt算子的偏微分方程图像去噪模型[J].计算机应用,2013,32(12):3385-3388.
[8]郝岩,许建楼.迭代重加权的小波变分修复模型[J].电子与信息学报,2013,35(12):2916-2920.
[9]AndrejCherkaev.Variationalmethodforoptimalmultimaterialcompositesandoptimaldesign[J].InternationalJournalofEngineeringScience,2014,83(12):162-173.
[10]AsgharGhorbani,JafarSaberi-Nadjafi.AneffectivemodificationofHe’svariationaliterationmethod[J].NonlinearAnalysisRealWorldApplications,2009,10(5):2828-2833.
[11]陈学松,刘富春.一类非线性动态系统基于强化学习的最优控制[J].控制与决策,2013,12(3):20-23.
[12]汪友明,吴青,王文庆.偏微分方程的算子自定义小波解耦算法研究[J].计算机仿真,2013,30(2):261-264.
[13]SAKhuri,ASayfy.Variationaliterationmethod:Green’sfunctionsandfixedpointiterationsperspective[J].AppliedMathematicsLetters,2014,32(10):28-34.
Variation iteration method in optimal control ofpartialdifferentialequations
JIANG Bin
(Department of Management & Information Technology, Nantong Vocation & Technical Shipping College, Nantong 226000, China)
Themaximumprincipleisusedtogettheoptimalconditionsofpartialdifferentialequation,andthenvariationiterationmethodisappliedtosolvetheHamilton-Pontryaginequation.Withtwoclassicalexamplesofoptimalcontrol,themathematicalmodelandalgorithmsimulationshowthatitiseffectiveandfeasible.
variationiterationmethod;partialdifferentialequations;optimalcontrol;maximumprinciple.
2016-05-10
江苏省教育科学“十二五”规划重点资助课题(苏教科规领[2015]1号); 南通航运职业技术学院院级课题(2013HYJY/18)
姜彬(1980-),男,汉族,江苏如皋人,南通航运职业技术学院讲师,硕士,主要从事人工智能与智能系统方向研究,E-mail:jiangb_nt@163.com.
10.15923/j.cnki.cn22-1382/t.2016.4.08
TP273
A
1674-1374(2016)04-0348-08

