无刷直流电机滑模观测器参数优化设计方法

武紫玉，王海峰，顾国彪

（1.中国科学院电工研究所，北京 100190；

2.中国科学院大学信息科学与工程学院，北京 100190）

无刷直流电机滑模观测器参数优化设计方法

武紫玉1，2，王海峰1，顾国彪1

（1.中国科学院电工研究所，北京 100190；

2.中国科学院大学信息科学与工程学院，北京 100190）

滑模反电势观测器的增益参数会影响观测器的收敛速度以及动态响应性能，常见的设计方法是基于观测器稳定性理论进行设计。提出一种利用遗传算法在稳定域内搜索观测误差最小的增益参数的新方法，既减少了参数设计时间，同时能够降低观测器的误差。为了改进传统遗传算法易陷入局部收敛的问题，采用多种群遗传算法求解最优增益参数。实验结果表明提出的方法能够快速求解最优反馈参数，并且观测器误差较小。

无刷直流电机；遗传算法；滑模观测器

永磁无刷直流电机（BLDCM）感应的反电势波形为方波，与永磁同步电机（PMSM）相比，BLDCM具有功率密度大、控制简单的优点。在一个电周期内BLDCM仅需要检测6个换相点，不需要实时观测转子位置。利用霍耳传感器，BLDCM可以很容易获取换相信号。但是，在特殊情况下，例如电机转轴无法安装霍耳传感器，或者在高温高湿的工作环境下传感器将会失效，那么无传感器控制算法则十分必要。

目前，常见的BLDCM无位置传感器控制算法有：反电势过零检测法、3次谐波电压检测法、反向二极管续流检测法、观测器法等。反电势过零检测法最为简单，但低速时精度较差［1］；3次谐波电压检测法适用在更宽的速度范围内，由于3次谐波反电势的频率为基波的3倍［2］；反向二极管续流检测法通过检测二极管的通断得到电机换相点，这种方法在低速时较其他方法性能好，但是需要采用6路独立供电系统对二极管电流进行检测，硬件电路复杂［3］；滑模观测器法（SMO）通过测量电机的电压和电流，构建变结构观测器模型对电机反电势进行在线辨识，利用辨识到的反电势过零点指导BLDCM换相。采用变结构模型，SMO对测量噪声和系统参数不确定性具有良好的抗干扰性，可以省去滤波器且具有良好的动态性能［4-5］。因而，滑模观测器被应用于永磁电动机的无位置传感器控制中。

滑模观测器的建立首先需要选择滑模面，系统稳定时将保持在滑模面上运动。其次需要设计滑模控制律，使系统能够在有限时间内从初始状态运行到滑模面上。SMO收敛速度的快慢以及稳态抖动均会受到滑模增益参数的影响。依靠李雅普诺夫稳定性判据，可以得到滑模增益参数的取值范围。本文提出采用遗传算法在稳定域内搜索最优的增益参数，减少了人工调试的工作量，并且能够减小SMO的观测误差。

1　反电势滑模观测器

1.1BLDCM数学模型

假设PMBLDCM电机非饱和，三相绕组对称，绕组电感值不变，并且忽略铁耗，那么在静止坐标系下，BLDCM的电压方程可以表述为

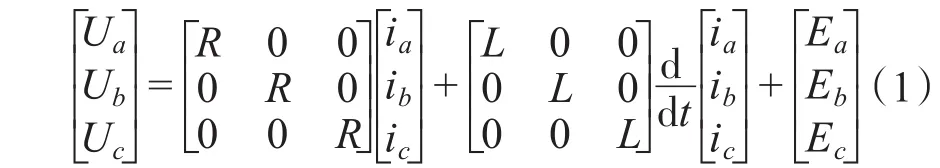
式中：R为定子电阻；L=Ls-Lm，Ls为定子自感，Lm为互感；Ux，ix，Ex（x=a，b，c）分别为三相电压、电流以及反电势。

考虑到线反电势过零点即为BLDCM换相点，因此将线电流和线反电势作为状态变量，构建状态方程如下式所示：

由于系统采样周期比电磁时间常数和机械时间常数小，因此可以认为反电势导数为0。

1.2滑模观测器的设计

选取滑模面如下：

考虑到饱和函数sat比传统的符号函数动态性能更好，一定程度上能够减小抖振，因此构建BLDCM反电势滑模观测器如下：

其中

式中：k1，k2，k3，k4为滑模增益常数。

将式（2）式与式（4）作差，考虑电机运行过程中随着绕组温度升高定子电阻发生改变，那么误差方程可表示为

式中：Δa11=-ΔR/L；e1，e2为线电流误差；e3，e4为线反电势误差。

根据李雅普诺夫稳定性理论，当系统误差满足下式时，系统满足到达滑模面的条件，ei为电流误差。

结合式（5）可以得到

若电阻误差为零，可得到

带入反电势误差方程中，可以得到

选择k3为负，那么反电势误差将随时间以指数形式收敛到0，最终反电势观测值等于实际值。同理可得k4＜0。

1.3基于遗传算法的SMO最优参数搜索

按照 1.2节的分析，选择 ΔRmax=2R，，结合电机参数，可以得到滑模增益常数k1～k4的范围。

在设计滑模反电势观测器时，通常根据设计经验，在满足稳定性的范围内选择合适的k1～k4。但是，这种方法过于依赖经验，并且需要多次调试才能确定最合适的增益参数值。为了解决这一问题，本文提出采用遗传算法的方法搜索最优的滑模增益常数值。

利用遗传算法搜索最优的滑模观测器增益参数，算法基本原理见图1。

图1　基于GA的SMO反馈增益辨识原理图Fig.1　Schematic diagram of SMO feedback gain identification based on GA

将SMO辨识的反电势误差作为适应度函数F为

将仿真得到的适应度值输入给遗传算法，遗传算法按照适应度值最小的原则进行搜索，找到F值最小对应的个体k1～k4。

由于电机三相绕组完全对称，反电势观测器eab与eca对称。为了减小搜索计算量，认为理想反馈增益k1=k2，k3=k4。那么，待搜索个体数由4个降低为2个。当进化代数达到最大限制时，GA停止搜索，输出最优的反馈增益个体到SMO中，SMO辨识的反电势提供换相位置，从而实现BLDCM的无位置传感器控制。

2　仿真实验

为了验证本文提出的参数设计方法，在Matlab/Simulink中搭建了无刷直流电机SMO仿真模型，编写了遗传算法程序以及接口函数。实验电机的参数为：额定电压310V，额定电流5.4A，额定转矩6 N·m，定子电阻1.43 Ω，额定转速2 000 r/min，定子电感4.21 mH，额定功率1 200 W，极数=8。

2.1单种群搜索仿真结果

按照1.3节的分析，将2个待辨识参数的取值范围设置为2.768×105＜k1＜1×108，-1×109＜k3＜0，最大进化代数设为100。通过搜索计算得到最优反馈增益参数分别为k1=2.768×105，k3= -2.296 2×106，进化过程见图2。由图2可知，初始种群适应度值较差，随着进化代数的增加适应度值逐渐下降，即SMO观测误差越来越小。遗传算法在60代左右收敛，超过60代后适应度函数值不再下降。

图2　遗传算法搜索过程Fig.2　Search process of genetic algorithm

将k1，k3带入SMO模型中，得到SMO观测的反电势与真实反电势波形对比，见图3。由图3可知，观测到的反电势基波幅值达到424，实际反电势基波幅值为270，并且，观测到的反电势相角超前实际反电势，观测器存在稳态误差。可见采用单种群遗传算法进行搜索时，仅仅找到了反馈参数的局部最优解，并没有找到全局最优的解。

图3　利用GA求解的SMO性能Fig.3　Performance of the SMO solved by GA

2.2多种群搜索仿真结果

单种群遗传算法存在局部收敛的问题，这是由于遗传算法的全局收敛是基于初始种群及进化代数无限大，而在实际计算时是无法实现的。另一方面，当种群中某个个体适应度优于其他个体，那么下一代群体很快被该个体控制，群体会失去竞争性，从而不再进化。此外，遗传算法的过早收敛还与交叉、变异算子的设置、初始种群个体分布情况、最优解的分布这些因素有关。

为了改善标准遗传算法（SGA）易陷入局部收敛，本文提出采用多种群遗传算法（MPGA）进行求解。MPGA算法的结构图如图4所示，图4中种群1～N均按照常规的GA进行进化，采用轮盘赌进行选择、交叉和变异。不过，与SGA不同之处在于：MPGA算法中每个种群可以设置不同的交叉概率和变异概率参数，从而实现不同的搜索目的；各个种群之间依靠移民算子联系，实现种群间的协同进化；采用最优个体、最少保持代数作为搜索终止判据，较SGA人为设置最大遗传代数更为合理。

图4　MPGA算法结构示意图Fig.4　Schematic diagram of MPGA

由于编写的MPGA算法将最大适应度函数值作为进化依据，因此，将适应度函数重新定义为

个体范围的设置与SGA算法相同。采用MPGA求解的最优解个体为 k1=421 640，k3=-998 917，算法搜索过程以及观测器性能对比见图5和图6。由图5可知，MPGA算法在局部收敛时能够快速跳出，继续进行优化搜索，最大进化代数为25代，计算时长明显缩短。由图6可知，SMO观测的反电势幅值与真实值波形十分接近。对观测到的反电势和实际反电势波形进行FFT分解发现，电机稳定运行时，实际Eab基波幅值为270，观测到的Eab为247，二者较为接近。不过，观测到的反电势相位滞后，在进行无位置传感器控制时需要进行相位补偿。

图5　MPGA算法搜索过程Fig.5　Search process of MPGA

图6　利用MPGA求解的SMO性能Fig.6　Performance of the SMO solved by MPGA

两种搜索算法对比见表1。

表1　两种搜索算法对比Tab.1　Comparison of the two kinds search algorithm

由表1可知，采用多种群遗传算法，算法收敛需要的代数明显减小，相应的搜索时间减小。并且，算法的适应度值也得到改善，即观测器的观测误差减小。

3　结论

滑模观测器模型对噪声具有较强的抗干扰能力，能够省去滤波电路，简化硬件电路，因而越来越多地被用在BLDCM无位置传感器控制中。观测器反馈增益参数的设计会影响SMO的收敛速度、稳态抖动以及稳态误差。本文提出采用MPGA算法求解最优反馈增益参数，既减少了人工调试时间，同时又降低了观测器误差。

需要注意的是，受计算机步长和计算量的限制，MPGA算法搜索到的最优解仍存在相位误差，并非全局最优解。在实际进行无位置传感器控制时，需要对观测到的反电势进行相位补偿。

［1］ Damodharan P，Vasudevan K.Sensorless Brushless DC Motor Drive Based on the Zero-crossing Detection of Back Electro⁃motive Force（EMF）from the Line Voltage Difference［J］.En⁃ergy Conversion，IEEE Transactions on，2010，25（3）：661-668.

［2］ Shen J X，Iwasaki S.Sensorless Control of Ultrahigh-speed PM Brushless Motor Using PLL and Third Harmonic Back EMF ［J］.Industrial Electronics，IEEE Transactions on，2006，53 （2）：421-428.

［3］Ogasawara S，Akagi H.An Approach to Position Sensorless Drive for Brushless DC Motors［J］.Industry Applications，IEEE Transactions on，1991，27（5）：928-933.

［4］Fakham H，Djemai M，Busawon K.Design and Practical Im⁃plementation of a Back-EMF Sliding-mode Observer for a Brushless DC Motor［J］.Electric Power Applications，IET，2008，2（6）：353-361.

［5］ 郭鸿浩，周波，左广杰，等.无刷直流电机反电势自适应滑模观测［J］.中国电机工程学报，2011，31（21）：142-149.

Brushless DC Motor Sliding Mode Observer Parameters Design Method

WU Ziyu1，2，WANG Haifeng1，GU Guobiao1
（1.Institute of Electrical Engineering，Chinese Academy of Sciences，Beijing 100190，China；
2.School of Information Science and Engineering，University of Chinese Academy of Science，Beijing 100190，China）

SMO gain parameters will affect the convergence rate and dynamic response speed of the observer. The common method designs gain parameters based on lyapunov theory.Proposed a new method to determine the gain parameters of SMO，which applies genetic algorithm（GA）to search the smallest observation error gain parameters in stable domain.The proposed method reduced the manual debugging time and the error of the observer.In order to improve local convergence of GA，proposed a multi-population genetic algorithm method to obtain optimal gain parameters.The experiment results have shown that the optimal gain parameters can be solved fast by the proposed method，and the observer error is low.

brushless DC motor（BLDCM）；genetic algorithm；sliding mode observer

TM315

A

2015-06-19

修改稿日期：2016-01-11

武紫玉（1988-），女，博士，Email：wuzy@mail.iee.ac.cn