带0-1和线性约束的特殊三次规划问题的全局最优性条件
周 莉
(重庆师范大学数学科学学院,重庆401331)
带0-1和线性约束的特殊三次规划问题的全局最优性条件
周 莉
(重庆师范大学数学科学学院,重庆401331)
研究了一类带有不等式约束和0-1约束的特殊三次规划问题的全局最优性条件,给出了此问题的一个全局最优性充分必要条件.同时通过数值例子来说明给出的全局最优性充分必要条件是很容易验证的.
三次规划问题;全局最优性条件;0-1约束;线性不等式约束
本文考虑如下带有的线性约束和0-1约束的特殊三次规划问题:
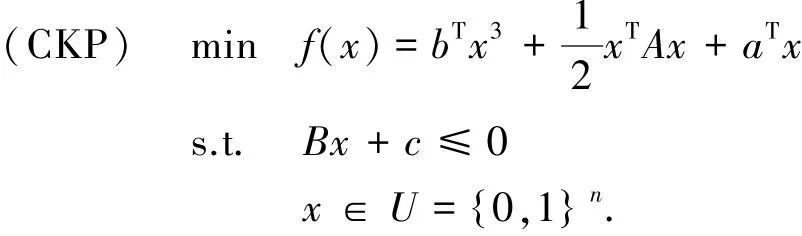
其中:a,b∈Rn,c∈Rm,B∈Rm×n,A为实对称矩阵.令,并设S≠Φ.
三规划问题具有很广泛的应用,在金融、农业、证券投资组合等方面都有广泛的应用[1-3].而三次问题的研究成果可以应用到二次规划问题,同时也丰富了二次规划的理论[4-6].文献[4]是刻画了二次背包问题的全局最优性充分必要条件;文献[7]利用拉格朗日函数和L-次微分的方法给出了带有二次等式约束,二次不等式约束以及双值约束的二次规划问题的全局最优性充分条件;文献[8]利用同样的方法给出了一类带有二次约束的三次规划问题的全局最优性充分条件;文献[9-10]是利用L-次微分给出了带有箱子或双值约束的特殊三次规划问题的全局最优的充分性条件和必要性条件;文献[11]利用二次上下估计法给出了一类带有箱子约束或双值约束的特殊三次规划问题的全局最优条件.本文主要研究了带有不等式约束和0-1约束的特殊三次规划问题的全局最优性,给出了此问题的全局最优性充分必要条件,并利用例子与文献[7-8,12-13]的所得到的全局最优性充分条件作对比,说明本文所给出的充要条件是很容易验证的,该充要条件仅用到了原问题的数据.
1 预备知识
R表示实线性空间,Rn表示n维欧几里得空间.对于向量x,y∈Rn,x≥y表示对于任意的i=1,2,…,n有xi≥yi,记号A≽B⇔A-B是半正定矩阵.I为单位矩阵,对任意的x=(x1,x2,…,xn)T∈Rn,用X=diag(x1,x2,…,xn)对角元素为x1,x2,…,xn的对角矩阵,因此x=Xe,其中e为单位向量.
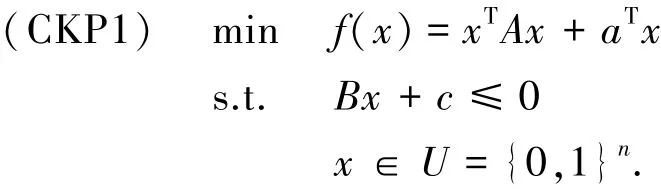
对于二次背包问题:其中:a∈Rn,c∈Rm,B∈Rm×n,A为实对称矩阵.令S={x∈U|Bx+c≤0},并设S≠Φ.对于,令为了方便研究,本文引进下面一些记号,令:
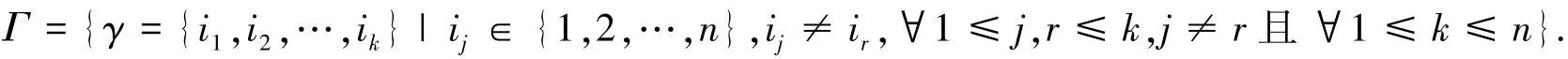
显然Γ是有限集,它取决于n的值.
对于对称矩阵A=(aij)n×n,a=(aj)n×1=(a1,a2,…,an)T∈Rn和γ={i1,i2,…,ik}∈Γ,令:
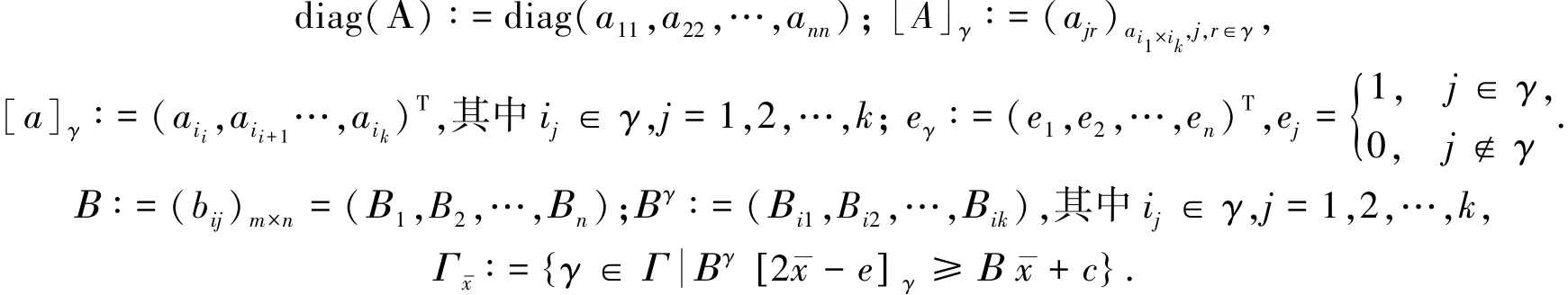
在文献[4]中,给出了问题(CKP1)的一个全局最优性充要条件,本文将利用这个结论给出问题(CKP)的一个全局最优性充要条件.
引理1[4](问题(CKP1)的全局最优充要条件)设,则是问题(CKP1)的一个全局极小点当且仅当下面的条件[NSC1]成立:
2 主要结果
证明 因为x3=x,所以,问题(CKP)问题可以转化成(CKP1)的形式来研究,再根据引理1可以得到:如果x 是问题(CKP)的一个全局极小点当且仅当条件[NSC]成立.
在文献[7]中,利用拉格朗日函数的抽象次微分研究了带有二次约束和双值约束的二次规划问题的全局最优性充分条件;文献[8]中,利用拉格朗日函数的抽象次微分研究了带有二次约束的一类特殊三次规划问题的全局最优性充分条件,该目标函数和本文的一致.利用文献[7-8]的方法可以得到本文问题(CKP)的一个全局最优性充分条件,具体描述如下:对于问题(CKP),设若存在λ∈Rm+和对角矩阵Q=diag(q1, q2,…,qn),qi∈R,i=1,2,…,n,且对任意的x∈S,有下列条件成立:
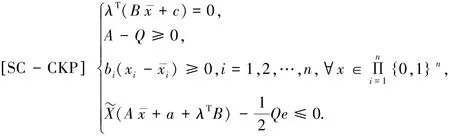
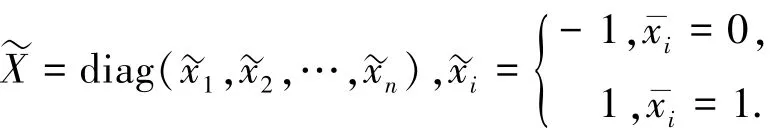
易知,本文所给出的全局最优性充要条件[NSC]是条件[SC-CKP]的推广.一方面,条件[NSC]仅用到了原问题的数据,而条件[SC-CKP]要讨论λ∈Rm+和对角矩阵Q的存在性;另一方面,[NSC]是全局最优性充分必要条件,而[SC-CKP]仅是全局最优性充分条件.下面通过如下例子来说明.
例1
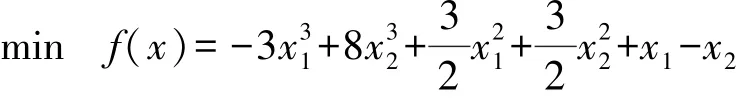

令a=(1,-1)T,b=(-3,8)T,r=(3,3)T,A=diag(r)T,B=(1,-1)T,c=-2,下面考虑点
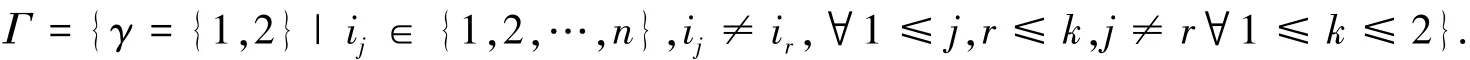
下面用充分条件[SC-CKP]来判断.
设对角矩阵Q=diag(q1,q2),qi∈R,i=1,2,λ∈Rm+,这里m=1.因为x=(1,0)T,所以diag(x)=diag(1,-1),计算可得A-Q=diag(3-q1,3-q2),则:
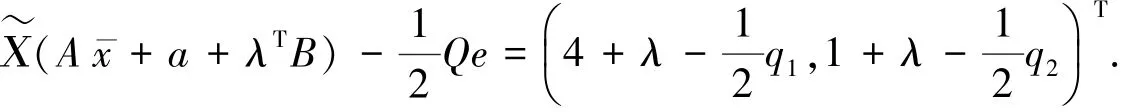
假设A-Q≽0可得:q1≤3,q2≤3,由
综上可以得到λ≤-5/2,λ≥1/2.因此,不存在拉格朗日参数λ>0,使得条件成立.但由本文的方法知x=(1,0)T是全局最优解.所以,条件 [SC-CKP]只是充分条件,而不是必要条件.
[1] HENIN C,DOUTRIAU J.A specia1ization of the convex simp1ex method to cubic programming[J].Decis Econ Finance,1980,3:61-72.
[2] HANOCH G,LEVY H.Efficient portfo1io with quadratic and cubic uti1ity[J].J Bus,1970,43:181-189.
[3] Levy H,Sarnat M.Investment and portfo1io ana1ysis[M].New York:Wi1ey,1972.
[4] WU Z Y,YANG Y J,BAI F S,et a1.G1oba1 optima1ity conditions and optimization oethods for quadratic knapsack prob1em[J].Journa1 of Optimization Theory and App1ications,2011,151(2):241-259.
[5] LI G Q,WU Z Y,uan J.A new 1oca1 and g1oba1 optimization method for mixed integer quadratic programming prob1ems[J].App1ied Mathematics and Computation,2010,217(6):2501-2512.
[6] WU Z Y,LI G Q,Quan J.G1oba1 optima1ity conditions and optimization methods for quadratic integer programming prob1ems[J].Journa1 of G1oba1 Optimization,2011,51:549-568.
[7] WU Z Y,JEYAKUMAR V,Rubinov A M.Sufficient conditions for g1oba1 optima1ity of biva1ent nonconvex quadratic programs with inequa1ity constraints[J].Journa1 of Optimization Theory and App1ications,2007,133:123-130.
[8] 叶敏,李国权.带有二次约束的一类特殊多项式规划问题的全局最优性充分条件[J].重庆师范大学(自然科学版),2014,31(3):17-20.
[9] WANG Y J,LIANG Z A.G1oba1 optima1ity conditions for cubic minimization prob1em with box or binary constraints[J].Journa1 of G1oba1 Optimization,2010,47:583-595.
[10] ZHANG X M,WANG Y J,Ma W M.G1oba1 sufficient optima1ity conditions for a specia1 cubic minimization prob1em[J].Mathematica1 Prob1ems in Engineering,2012,3(7):178-192.
[11] 周雪刚.具有超矩形约束的三次规划的全局最优性条件[J].重庆师范大学学报(自然科学版),2014,31(4):21-25.
[12] 周莉,李国权.带混合约束的特殊三次规划问题的全局最优性充分条件[J].重庆工商大学学报(自然科学版),2015,32(9):16-19.
[13] 叶敏.双值约束三次规划问题的全局最优性充分条件[J].重庆工商大学学报(自然科学版),2015,32(7):48-51.
责任编辑:时 凌
Global OPtimalitY Conditions for a SPecial Cubic Minimization Problem with 0-1 and Linear Constraints
ZHOU Li
(Schoo1 of Mathematics,Chongqing Norma1 University,Chongqing 401331,China)
In this artic1e,we considered a specia1 cubic optimization prob1em with 0-1 and 1inear inequa1ity constraints.We give necessary and sufficient conditions of g1oba1 optima1ity for this specia1 cubic optimization prob1em.Numerica1 examp1es are a1so presented to show that the proposed optima1ity conditions are efficient.
cubic minimization prob1em;g1oba1 optima1ity conditions;0-1constraints;1inear inequa1ity constraints
O221
A
1008-8423(2016)02-0153-03
10.13501/j.cnki.42-1569/n.2016.06.010
2016-01-21.
重庆市自然科学基金项目(CSTC2013JLYJa00021);重庆师范大学校级研究生科研创新项目(YKC15012).
周莉(1990-),女,硕士生,主要从事最优化理论与算法的研究.

