基于三电平逆变器的新型无扇区SVPWM优化算法

吴承天，王鲁杨，程肖肖，郭永哲，姜肇建

（1.上海电力学院电气工程学院，上海 200090；2.国网上海市电力公司市区供电公司，上海 200080；3.国网上海市南供电公司，上海 201199）

基于三电平逆变器的新型无扇区SVPWM优化算法

吴承天1，王鲁杨1，程肖肖2，郭永哲3，姜肇建1

（1.上海电力学院电气工程学院，上海 200090；2.国网上海市电力公司市区供电公司，上海 200080；3.国网上海市南供电公司，上海 201199）

空间矢量控制脉宽调制技术（SVPWM）由于其电压利用率高、谐波含量相对少、易于数字化实现等优点迅速成为近年来的研究热点。传统的三电平SVPWM算法需要三角函数的运算，耗时。而且要先判断大扇区后判断小扇区，各种判断方法表达式也不统一。通过对基于传统的三电平SVPWM算法上进行深入的研究分析，提出120°坐标系的无扇区空间矢量调制方法。通过基本矢量的动作规律进行优化安排，避开传统三电平的大小扇区判断，动态实现每个矢量的动作安排。相比于传统的三电平空间矢量调制技术，新的算法化简了过程步骤，更易于数字实现，大大提高了运算速度。在Matlab环境下的仿真验证了结论的正确性及可行性。

空间矢量脉宽调制；120°坐标系；无扇区；动态矢量优化

传统的SVPWM逆变控制的优点在于电压利用率高，能提高15%；输出电压或电流的谐波畸变率相对较小；利用数字化控制有利于实际操作性，缺陷在于运算的复杂性。传统的SVPWM需要大量的三角运算，耗时。许多学者针对其缺点进行研究改进［1-8］，希望能保留和发展传统SVPWM的优势，同时改进算法上的劣势。文献［3］通过改变扇区的划分，一定程度上简化了电压矢量作用时间上的运算；文献［6］用两电平SVPWM算法的多层叠加实现三电平SVPWM算法，虽然避开了小扇区判断并减少一定的计算量，但仍没有脱离两电平中的大扇区判断，还增加了判断矢量的平移算法。文献［1］和文献［7］通过SVPWM的本质，用三相电压磁链守恒的方式提出了无扇区的算法，但该方法易于两电平的实现，难以推广到三电平或者更高电平逆变的情况。本文通过对传统SVPWM的坐标系进行变换，结合传统坐标系矢量动作规律和120°坐标系的三角形特点，提出一种无扇区判断方法，在传统的固定7段式矢量安排的基础上，进行动态的矢量安排。该算法避开了传统大小扇区判断的概念，将整个矢量空间化整为零，视为一个小三角动作区域，再由小三角区域推广到整个矢量空间。同时自动判断7段式矢量安排的首个动作矢量，进而完成整个区间的动作过程。与传统的SVPWM算法相比，新算法提高了运算的速度，更有利于数字实现。

1　传统SVPWM逆变算法

图1为传统中点钳位三电平逆变拓扑结构（three-level neutral point clamped，3L-NPC）。其中UD为直流侧。

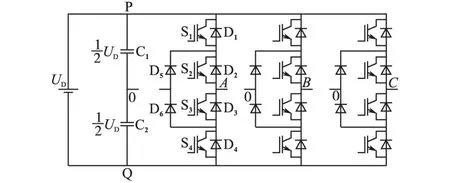
图1　三电平中点钳位逆变拓扑结构Fig.1　Topology of three-level NPC inverter

传统的三电平逆变一共有27个矢量，其中有效矢量19个。首先要经过大小扇区判断来确定作用的3个矢量。以大扇区Ⅰ为例，通过4个判断表达式确定参考矢量所在的小扇形区域。

4个判断表达式如下：

式中：Vα，Vβ为参考矢量在直角坐标轴上的分量。

在对确定的基本矢量进行时间计算的过程中可以得出，传统SVPWM逆变控制需要大量的三角函数运算，式（1）～式（4）只是小扇区的一种判断表达式。

最后采用7段式矢量安排，因为7段式矢量动作的后半段与前半段对称，表1给出了扇区Ⅰ各小扇区前半段的矢量安排。

表1　扇区Ⅰ各小扇区矢量作用顺序Tab.1　The sequence of vector action of each inner sector in section I

对表1进行深入分析和推广，将小区域1，2 和4，5合成1个区域，能得到如下结论：在7段式前半段的矢量安排中，当Vref处于正三角形区域时，矢量的安排体现顺时针性；当Vref处于倒三角形区域时，矢量的安排体现逆时针性。

2　三电平无扇区SVPWM逆变优化算法

2.1120°坐标系的建立和变换

在传统的三电平SVPWM算法基础上提出一种新的控制算法——基于120°坐标系的无扇区SVPWM优化算法。

建立120°坐标系，g轴为横轴与直角坐标系的x轴重合，h轴为g轴逆时针旋转120°，如图2所示。

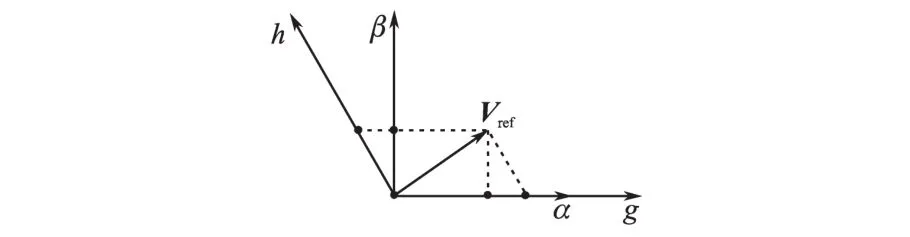
图2　120°坐标系空间矢量坐标系Fig.2　120°coordinate space vector coordinate system

设参考矢量Vref在直角坐标系下坐标为（Uα，Uβ），在g-h坐标系下坐标为（Ug，Uh），由于参考矢量固定，可得到下式：

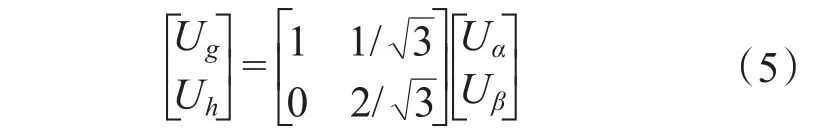
再通过Clark变换，可以得到abc三相电压在120°坐标系下的形式，见下式：

在120°坐标系下，矢量从三角函数运算变换为整数运算，能大大降低系统运算的速度。

2.2基本矢量的确定

对于任意参考矢量，选取其所在的三角形区域的3个矢量为基本矢量。

首先要选取距离参考矢量最近的4个矢量，这4个矢量是由参考矢量在g轴和h轴上投影的上下取整所组成的4个矢量，见图3a。

因此4个基本矢量分别为：Ucc，Ucf，Ufc，Uff，c代表ceiling，向上取整，f代表floor，向下取整。

由图3可以看出，Ucc，Uff为其中2个确定的基本矢量，如图3b所示。第3个矢量由参考矢量终点的平行方程表达式确定。

假设：

为经过参考矢量Vref终点的方程，当k≥Ugc-Uhc时，Vref落在正三角形内，此时选取Ucf为第3个基本矢量；反之，Vref则落在倒三角形内，此时去Ufc为第3个基本矢量。

图3　基本矢量选取Fig.3　Basic vector selection

2.3矢量作用顺序动态化

通过归纳传统三电平矢量顺序的安排结合120°坐标系的三角形特点，提出一种动态化的矢量顺序安排，并能推广到任意多电平逆变的SVPWM逆变控制策略。

基本矢量选取过程中，定义U1=Uff，U2=Ucc，U3=Ucf或Ufc。由表1整理的前半段矢量安排可以看出：当Vref在正三角形区域时，矢量动作体现顺时针性，结合120°坐标系的三角形特点和3个基本矢量的定义，矢量动作顺序为1—2—3—1所在循环；当Vref在倒三角形区域时，矢量动作体现逆时针性，矢量的动作顺序仍然为1—2—3—1所在循环。如图4所示。

图4　矢量动作安排顺序Fig.4　Sequence of vector action

通过上述理论分析可以发现：在120°坐标系下，合成参考矢量的基本矢量是由Vref所在的三角形所确定的，无论Vref在哪个小三角形区域，基本矢量都是以固定的规律动作。新算法将整个空间矢量归一到一个小三角形，针对一个小三角的基本矢量安排即完成了整个空间矢量的安排。整个推导过程中没有牵涉到任何的扇区判断，大大化简了运算步骤。

2.4首矢量的确定及判定

基于上述理论分析，确定了7段式状态变化的原则，因此只要确定7段式的首个动作矢量，即完成了一个小三角形区域的SVPWM逆变控制，进而完成了整个120°坐标系下的SVPWM算法控制。

通过对传统三电平SVPWM控制算法所有7段式首矢量动作的罗列，可以发现以下规律：所有的首矢量均分布在内圈的正六边形上，如图5所示。

图5　首矢量分布规律Fig.5　The principle of first vector distribution

给出首矢量变化原则以及选取原则如下：所有首矢量的状态改变均以逆时针方向变化，选取内圈正六边形上的矢量为Vref所在小三角区域的首矢量。当参考矢量Vref落在小三角形中有2个可被选为首矢量时，优先选取能先达到内圈逆时针状态的矢量为首矢量。

3　优化算法步骤

3.1无扇区算法流程图

120°坐标系下无扇区SVPWM优化控制算法的流程图如图6所示。

图6　无扇区SVPWM算法流程图Fig.6　The algorithm diagram of no sector SVPWM

3.2首矢量确定流程图

首矢量确定是整个算法的重心，首矢量的确定需要分为2个步骤：首先确定合成Vref的基本矢量是否在内圈六边形上，其算法流程图见图7。

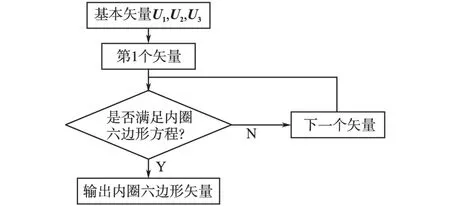
图7　内圈六边形矢量确定Fig.7　Vectors on inner hexagon qualification

当基本矢量中只有1个符合要求时，该矢量即为首矢量；当基本矢量中有2个在内圈六边形上时，通过图8所示流程图确定最终首矢量。

图8　首矢量算法流程图Fig.8　The diagram of fisrt vector selection

4　仿真验证

仿真验证在Matlab/Simulink环境下进行。其中，三相负载为对称阻感负载，R=1 Ω，L=0.1 mH，UD=380 V。

逆变输出结果见图9，从上至下分别是线电压、相电压以及相电流的波形。仿真时间为0.1 s，间隔采样时间为1e-5 s。

图9　阻感负载下线电压、相电压以及相电流波形Fig.9　Waveforms of line voltage，phase voltage and phase current with resistance-inductance load

对传统SVPWM控制算法与120°坐标系下无扇区的SVPWM控制算法进行仿真时间检测，结果得：在相同电路参数，采样精度均为1e-05 s以及仿真时间均为0.1 s的条件下，传统三电平SVPWM逆变控制算法耗时62 s，而120°坐标系无扇区SVPWM逆变优化算法耗时50 s，运算速度提高了19.35%。

5　结论

针对传统SVPWM逆变控制策略的缺陷，提出了一种基于120°坐标系下采用动态矢量规划无扇区的调制算法，该方法跳过了传统的大小扇区判断并将整个矢量运算统一到一个小三角区域来计算，通过一个小三角区域反映整个算法的规律性。

优化算法大大化简了中间计算过程，不仅如此，该算法思想可以推广到任意多电平的SVPWM逆变控制，仿真结果表明了新算法的有效性。

［1］ 方斯琛，李丹，周波，等.新型无扇区空间矢量脉宽调制算法［J］.中国电机工程学报，2008，28（30）：35-40.

［2］ 王永，沈颂华，关淼.新颖的基于电压空间矢量三相双向整流器的研究［J］.北京电工技术学报，2006，1（21）：104-109.

［3］ Peroutka Z，Glasberger T.Comparison of Methods for Continuous Transition of Space Vector PWM into Six-step Mode［C］// 12thIntemational Power Electronics and Morion Control Conference，Portoroz.2005.

［4］Zhang Xiaowei，Li Yongdong，Wang Wensen.A Noel Implementation of SVPWM Algorithm and Its Application to Three-phase Power Converter［C］//Power Electronics and Motion Control Conference，2000.

［5］ 谢东东，范波，赵伟刚.一种化简三电平SVPWM的感应电动机矢量控制方法［J］.微特电机，2013，41（6）：45-49.

［6］ 苏杭，陈东华，孙仲兵，等.一种无扇区判断SVPWM算法及仿真研究［J］.华电技术，2008，30（10）：27-30.

［7］ Jacobina C B，Nogueira Lima A M，da Silva E R C，et al.Digital Scalar Pulse-width Modulation：a Simple Approach to Introduce Nonsinusoidal Modulating Waveforms［J］.IEEE Transactions on Power Electronics，2001，16（3）：351-359.

［8］Ge B，Abu-Rub H，Peng F，et al.An Energy Stored Quasi-Z-source Inberter for Application to Photovoltaic Power System［J］.IEEE Trans.Ind.Electron，2013，60（10）：4468-4481.

Novel Algorithm of SVPWM Without Sector Calculation Based on Three-level Inverter

WU Chengtian1，WANG Luyang1，CHENG Xiaoxiao2，GUO Yongzhe3，JIANG Zhaojian1
（1.Electric Power Engineering，Shanghai University of Electric Power，Shanghai 200090，China；
2.Urban Power Supply Compary，SMPC，Shanghai 200080，China；3.SG Shanghai Shinan Electric Power Supply Comparry，Shanghai 201199，China）

Space vector pulse width modulation（SVPWM）get the hot-spot study rapidly for its high ratio of output voltage，low content of total harmonic distortion（THD）and digitization reality easier in recently years.Traditional SVPWM algorithm exists following disadvantage，such as too much trigonometric function to make the algorithm wasting too much time，judge the external section first and the interior section for the various expression principle etc. Established 120°coordinate system basis on traditional SVPWM algorithm′s further analysis，using the law of basic vector motion under the new coordinate character to optimized the vector arrangement at the meantime.This new algorithm avoided the judgment of external an interior section and mdke the dynamic vector arrangement implementation.Compared with the traditional SVPWM strategy，new algorithmic simplified the process of control strategies，mdke the digital implementation efficiently and boosted the operation.The model testifies the validity and feasibility of the conclusion under the circumstance of Matlab/Simulink.

space vector pulse width modulation；120°coordinate system；no sector；dynamic vector optimization

TM921

A

2015-10-12

修改稿日期：2016-01-19

吴承天（1990-），男，硕士研究生，Email：1078494540@qq.com