同步电机在位置随动系统中跟踪误差的分析与研究

王宏文，孟立新，吴红星，侯美杰

（河北工业大学 控制科学与工程学院，天津 300130）

同步电机在位置随动系统中跟踪误差的分析与研究

王宏文，孟立新，吴红星，侯美杰

（河北工业大学 控制科学与工程学院，天津 300130）

位置随动系统的任务是使被控量按同样规律变化并与输入信号的误差保持在规定范围内。同步电机具有响应快、定位准确特点，将其作为执行机构，满足系统要求。在建立位置随动系统的等效数学模型基础上，考虑到跟踪最终位置过程的不确定性和传统PID控制器超调量大，调节时间长的缺点，设计了Fuzzy-LQR-PID控制算法来提高位置跟踪精度，通过Matlab软件对该算法进行仿真，并由STEP7编程软件编写程序在自主研发的无头轧制多级传动系统的模拟实验台上进行了实验验证。实验结果表明：该方法设计的系统控制精度明显提高，可实现同步电机快速精确地跟踪，位置跟踪误差小于PID控制算法的1/4，同时优化了控制输入信号，有着广阔的应用前景。

线性二次型调节器；PID控制器；模糊控制；跟踪误差；Simulink仿真；STEP7

在随动控制系统中的驱动电机要求具有响应速度快、定位准确、转动惯量小等特点。在本实验台的无头轧制工艺过程中，当后一根钢坯追赶上前一根钢坯的时候，由同步电机驱动的焊机在两个钢坯对接处进行焊接。为了保证钢坯无头轧制的连续性，钢坯的焊接必须在移动中自动完成，整个过程是一个位置随动系统［1］。焊机的移动速度与钢坯的轧制速度必须严格同步来减小焊接和轧制钢坯间的机械耦合，这就对系统的位置跟踪特性提出了较高的要求。

对于PID控制方法，结构简单，鲁棒性强，但闭环动态品质对PID增益的变化太敏感，难以协调快速性与稳定性之间的矛盾，很难得到最优控制参数；采用线性二次型调节器（LQR）［2］可得到状态线性反馈的最优控制规律，以跟踪误差为优化目标，易于构成闭环最优控制。在位置随动系统中，由于焊接过程中被追赶钢坯位置的不确定性，导致焊接过程的位置曲线不稳定，由此提出了一种在基于LQR的PID算法之前加入模糊控制器进行动态补偿的方法。本文通过建立位置随动系统的等效数学模型，分别对PID控制器、Fuzzy-LQR控制器、Fuzzy-LQR-PID控制器进行跟踪误差分析，并通过联合仿真以及在模拟实验台上进行运行验证。

1　位置随动系统的数学模型

焊接过程的位置随动系统主要由位置控制器，位置测量元件，传动系统和执行机构组成。以交流电机作为执行机构，以变频器作为控制与放大装置的机电控制系统，由于变频器为矢量控制型，根据交流传动矢量控制思想，将变频器、同步电机和位置测量元件看成一个被控对象，对于永磁同步电机，转子磁通位置与转子机械位置相同，这样通过检测转子实际位置就可以得知电机转子磁链位置，从而使永磁同步电机的矢量控制比起异步电机的矢量控制大大简化。当id=0时，从电机端口看，永磁同步电机相当于1台他励直流电机［3］。当磁通Φ一定时，通过改变电枢电压可以实现调速。额定励磁下他励直流电动机的的电压平衡方程为

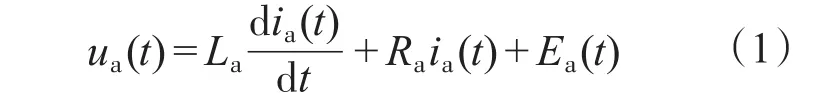
忽略黏性摩擦以及弹性转矩，直流电机的转矩平衡方程为

额定励磁下的电枢反电动势Ea和电磁转矩Te分别为

式中：TL为包括电机空载转矩在内的负载转矩；J为电动机轴上的转动惯量；Ce为电动机的电动势系数；Cm为电动机的转矩系数。

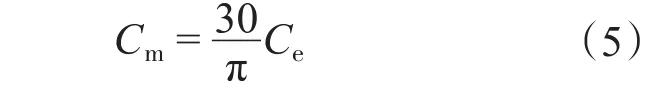
由式（1）～式（5），电机的相关参数为 PN= 1.36 kW；UN=400 V；IN=3.4 A；nN=3 000 r/min；Ra=94.12 Ω；La=0.225 H；J=1.89×10-6kg·m2；Ce= 0.05 V·s/rad。则等效的他励直流电机传递函数为

由于实际运行时电机转1圈焊机移动5 mm，则其位置与转速的关系为

随动系统的动态结构图如图1所示。相应的可得出其传递函数为

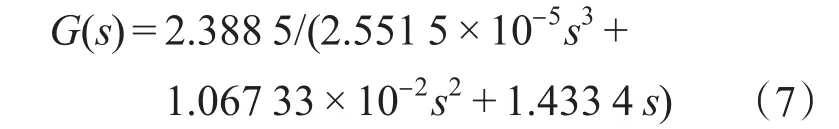
图1　位置随动控制系统的动态结构图Fig.1　Dynamic structure diagram of location servo control system

2　Fuzzy-LQR-PID控制器的设计

2.1LQR控制器设计

考虑到式（7）的线性系统，它是可控的或者至少是稳定的，LQR［4］的基本思想是基于状态方程 ẋ=Ax+Bu，选定二次型性能指标 J=∫（eTQe+uTRu）dt，并在选定最优加权矩阵Q，R的基础上寻找1个最优的反馈控制规律u（t）= Kx（t）的最优反馈增益矩阵K，使得在时间区间［t0,∞］内，将系统从非平衡状态迅速转移到零平衡状态附近。利用庞特里亚金极小值原理，可以使J为极小值的最优控制u（t）=-R-1BTPx（t），满足Riccati矩阵 PA+ATP-PBR-1BTP+Q=0，Matlab提供了较为方便的接口函数来求取Riccati方程，公式为［K,P］=lqr（A,B,Q,R），其中A为系统矩阵，B为控制矩阵，K为状态反馈向量，P为Riccati方程的解，Q，R为加权矩阵，根据系统要求的跟踪精度和系统的输出功率选定最佳权矩阵［5］。

2.2Fuzzy-LQR-PID控制系统

模糊控制可以简化系统设计的复杂性，特别适用于非线性、时变、滞后、模型不完全的系统控制。利用控制法则来描述系统变量间的关系用语言式的模糊变量来描述系统，具有较好的鲁棒性、适应性、强健性及较佳的容错性［6］，充分利用LQR控制器良好的稳态性能，通过对输入输出信号的误差进行PID控制，又进一步提高了系统的跟踪动态性能，由于钢坯焊接位置曲线的不确定性，将模糊控制器加入到LQR-PID控制器［7］前对输入信号进行前置滤波［8］，由此提出了Fuzzy-LQR-PID控制算法。由系统的控制要求可知模糊控制器是双输入双输出控制器，以位移s和速度v为输入信号［9］，u1和u2为输出信号。定义量化因子，把［-6，6］之间连续变化的量分成用模糊语言表示的不同等级，每个语言变量对应一个模糊集合，用模糊隶属度函数来表示，习惯上正大（PB）取在+6附近；正中（PM）取在+4附近；正小（PS）取在+2附近；零（ZO），取在0附近；负小（NS）取在-2附近；负中（NM）取在-4附近；负大（NB）取在-6附近。模糊隶属度一般定义为三角形式，其隶属度函数见图2。

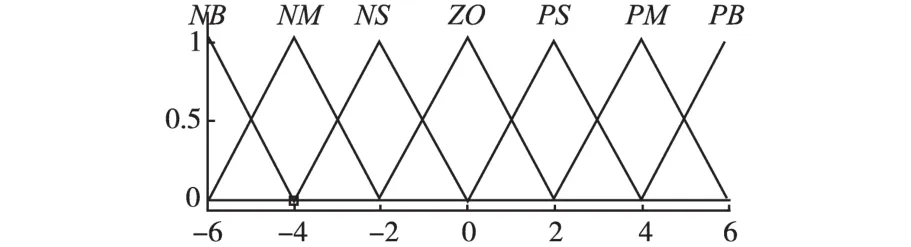
图2　隶属度函数Fig.2　Membership functions

根据被控对象与控制作用之间的一般变化规律，不同的控制对象的控制规则是变化的。由于不同阶段控制原则，模糊控制器输出信号u1和u2的模糊控制规则见表1和表2。

表1　模糊规则表（u1）Tab.1　Fuzzy control rule table（u1）

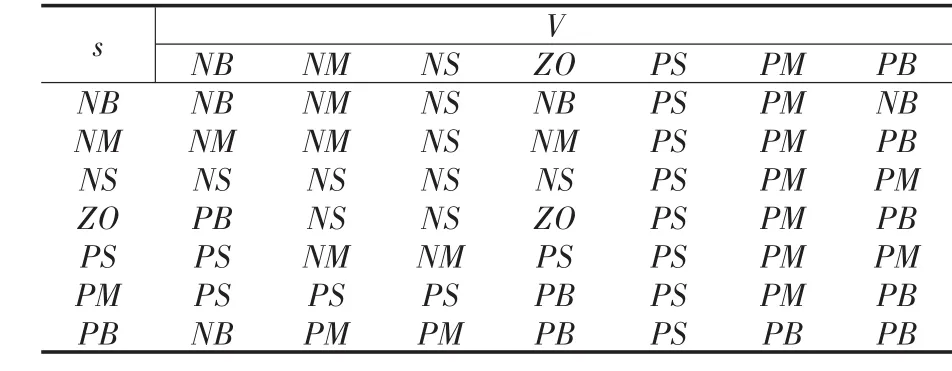
表2　模糊规则表（u2）Tab.2　Fuzzy control rule table（u2）

3　Matlab仿真与结果分析

在Matlab中利用指令“［A B C D］=tf2ss （num，den）”和“k=lqr（A，B，Q，R）”求得式（7）的以下相关矩阵

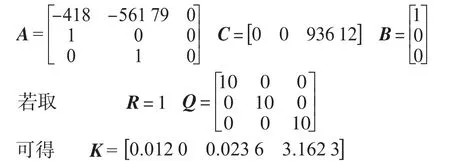
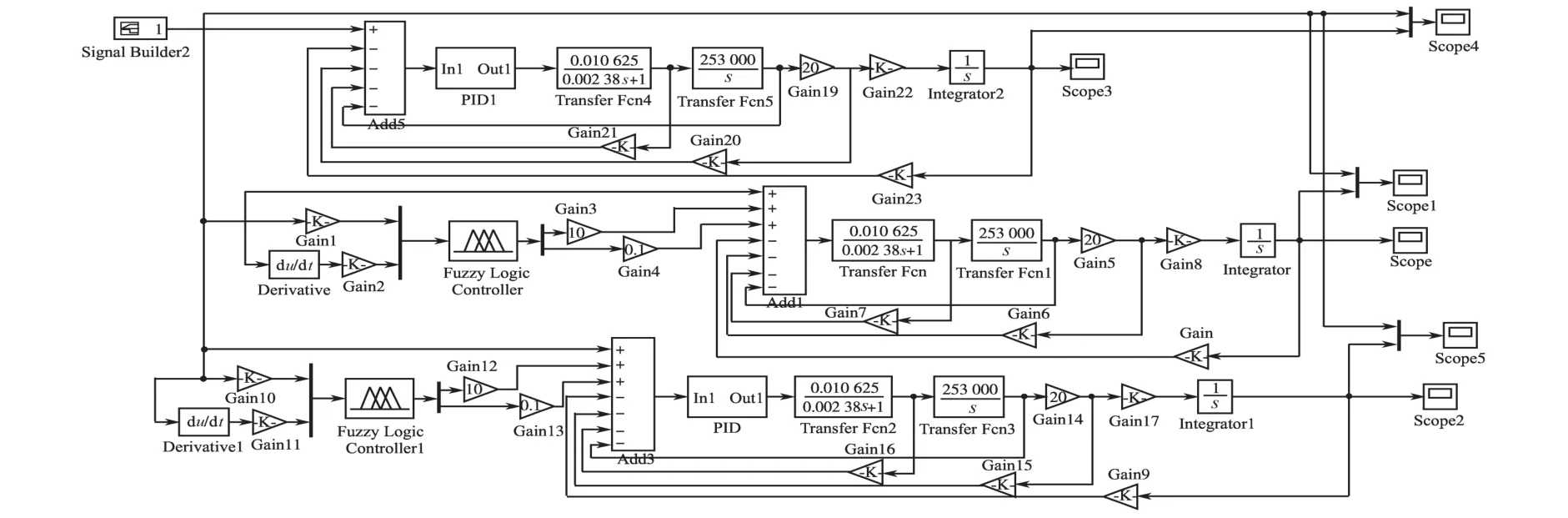
图3　LQR-PID控制、Fuzzy-LQR控制和Fuzzy-LQR-PID控制系统仿真图Fig.3　LQR-PID control，Fuzzy-LQR control and Fuzzy-LQR-PID control system simulation diagram

图4　Fuzzy-LQR-PID控制、Fuzzy-LQR控制和LQR-PID控制响应曲线Fig.4　LQR-PID control，Fuzzy-LQR control and Fuzzy-LQR-PID control response curves

由控制仿真图3可得到图4的仿真结果，通过比较可知Fuzzy-LQR-PID控制的焊机焊接过程的跟踪效果更好。

4　PLC编程并在实验台上进行验证

如图5所示，以S7-400［10］为核心连接各个模块，其中2台异步电机分别驱动2块钢坯，同步电机驱动焊机，当达到焊接条件时，焊机追踪钢坯完成焊接并通过WINCC组态［11］软件的人机界面来完成无头轧制模拟实验台的监控任务。在STEP7中完成整个系统的硬件组态和程序设计，逻辑控制和控制策略在西门子S7-400中实现。通过C语言，计算出离线模糊控制查询表见表3、表4。

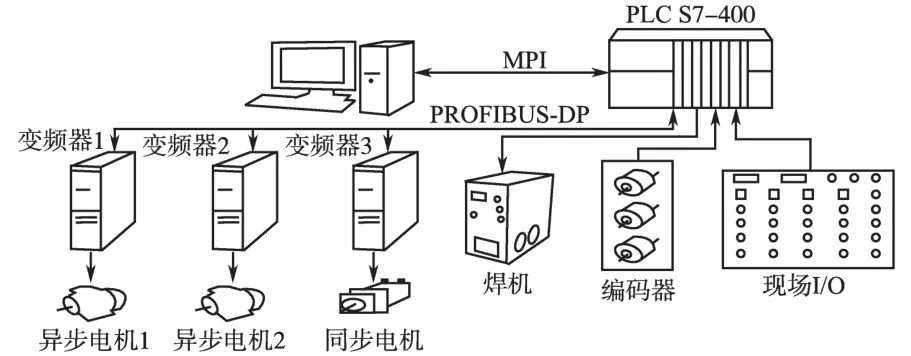
图5　无头轧制模拟实验平台的控制系统分布图Fig.5　Distribution diagram of the simulation platform of the endless rolling multi-drive transmission system

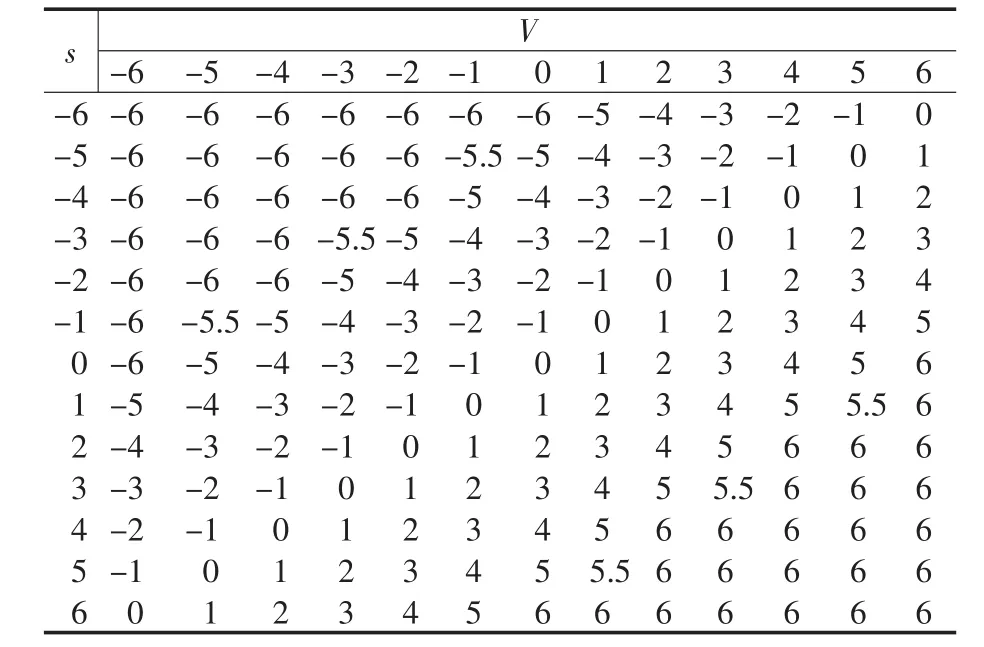
表3　模糊规则查询表（u1）Tab.3　Fuzzy rules lookup table（u1）

表4　模糊规则查询表（u2）Tab.4　Fuzzy rules lookup table（u2）

将其存于PLC数据块中并编制1个查询表子程序，每次使用时在子程序中调用即可，本文通过STEP7软件编程实现模糊控制算法［9］。运行的监控结果见图6～图8。由于本实验台考虑模拟钢坯的宽度为100 mm，焊接最终的误差应该减去100 mm。结果表明Fuzzy-LQR-PID控制在实现钢坯焊机焊接过程中节约10 s左右的时间，跟踪误差在2 mm以内，Fuzzy-LQR跟踪误差在4mm以内，PID控制的跟踪误差在8 mm以内。

图6　PID控制下的跟踪误差曲线Fig.6　Tracking error curves under PID control

图7　Fuzzy-LQR控制下误差控制曲线Fig.7　Tracking error curves under Fuzzy-LQR control

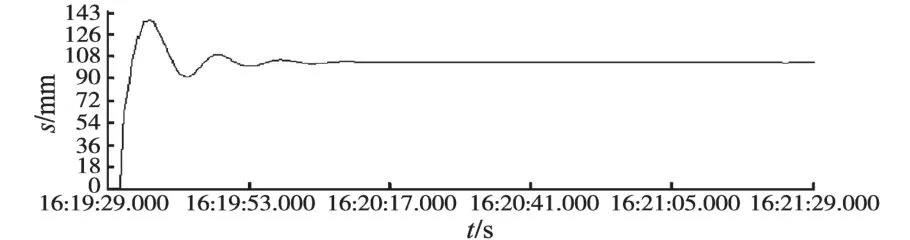
图8　Fuzzy-LQR-PID控制下的误差控制曲线Fig.8　Tracking error curves under Fuzzy-LQR-PID control

比较3种控制方式，列出表5，可知PID的动态跟踪效果最差，Fuzzy-LQR控制的动态跟踪精度比PID控制的方式提高了2倍。Fuzzy-LQR-PID控制的动态跟踪精度比Fuzzy-LQR控制的跟踪精度提高了2倍，比PID控制的方式提高了4倍。本文提出的算法是可行有效的。

表5　3种算法的性能参数比较Tab.5　Comparison of performance parameters of three kinds of algorithms

5　结论

1）Matlab软件具有高效的数值计算及符号计算功能；功能丰富的应用工具箱（如信号处理工具箱、通信工具箱等），为用户提供了大量方便实用的处理工具，组建各个模块建立模拟真实环境下相关参数变化和干扰，快速准确地验证控制系统的可行性。

2）LQR控制使选定的目标达到最优，但抗扰性差。PID控制原理简单，使用方便适应性强，鲁棒性强。从仿真结果看：将模糊控制，LQR控制与PID控制相结合，使系统响应速度更快，调节时间更短，跟踪精度更高，完全符合焊接过程中对位置随动系统的要求，具有一定的实际意义。

［1］ 王宏文，刘通学，刘丽，等.无头轧制多级传动模拟实验平台的研究与开发［J］.制造业自动化，2008，30（1）：23-26.

［2］ 吴受章.最优控制理论与应用［M］.北京：机械工业出版社，2008.

［3］ 陈伯时.电力拖动自动控制系统［M］.第3版.北京：机械工业出版社，2003.

［4］Miller，Daniel E.Near optimal LQR Performance for a Compact Set of Plants［J］.IEEE Transactions on Automatic Control，2006，51（9）：1423-1439.

［5］ 刘豹.现代控制理论［M］.第2版.北京：机械工业出版社，2000.

［6］ 李少远，王景城.智能控制［M］.第2版.北京机械工业出版社，2009.

［7］ 张明月，杨洪波，贾宏光.基于降维观测器的电动舵机PID_LQR控制［J］.计算机测量与控制，2013，21（7）：1800-1803.

［8］ Vimala Vindhya，Venkat Reddy.PID-Fuzzy Logic Hybrid Controller for a Digitally Controlled DC-DC Converter［C］//International Conference on Green Computing，Communication and Conservation of Energy（ICGCE），2013：362-366.

［9］ 王霞，朱景伟.基于模糊PI控制的无刷直流电机调速系统［J］.电气传动，2014，44（1）：63-69.

［10］廖常初.S7-300/400 PLC应用技术［M］.北京：机械工业出版社，2008.

［11］西门子（中国）有限公司自动化与驱动集团.深入浅出西门子WinCC V6［M］.第2版.北京：北京航空航天大学出版社，2004.

Analysis and Research on Synchronous Motor Tracking Error in the Position Servo System

WANG Hongwen，MENG Lixin，WU Hongxing，HOU Meijie
（School of Control Science and Engineering，Hebei University of Technology，Tianjin 300130，China）

Position servo system′s task is to change controlled variable by the same laws and keep the error of the input signal within a specified range.Synchronous motor with fast response and accurate positioning features，which as an actuator，can meet the system requirements.On the basis of the established“equivalent”mathematical models of the position servo control system，taking into account the uncertainty of the final position of the tracking process and the traditional PID controller has many shortcomings such as large overshoot，long regulation time，presentsed Fuzzy-LQR-PID control algorithm to improve the tracking accuracy.This arithmetic was simulated by Matlab software. Used STEP7 programming software to complete the design process of Fuzzy-LQR-PID control algorithm，and experiment was carried out on the simulation platform of the endless rolling multi-drive transmission system，which was developed by ourselves.The experimental results show that：the control precision of the system designed by the method is improved significantly，the proposed method can realize synchronous motor quickly and accurately tracking，location tracking errorislessthan1/4ofPIDcontrolalgorithm，whileoptimizingthecontrolinputsignal，hasbroadapplicationprospects.

linear quadratic regulator（LQR）；PID controller；fuzzy control；tracking error；Simulink simulation；STEP7

TP275

A

2015-05-12

修改稿日期：2015-10-19

王宏文（1957-），男，工学硕士，教授，Email：wanghongwen@hebut.edu.cn