悬索桥主缆抗弯刚度的数值分析

田海龙，陈　辉

(1.湖南路桥建设集团有限责任公司，湖南 长沙　410004；2.浙江金筑交通建设有限公司，浙江 杭州　310005)



悬索桥主缆抗弯刚度的数值分析

田海龙1，陈辉2

(1.湖南路桥建设集团有限责任公司，湖南 长沙410004；2.浙江金筑交通建设有限公司，浙江 杭州310005)

为了研究主缆抗弯刚度对悬索桥受力性能的影响，采用有限元参数化建模方法对某悬索桥进行了模拟，模型中考虑了边界条件、荷载形式和主缆线形等因素，分析了加劲梁和主缆位移、内力和应力的变化规律。结果表明，考虑主缆抗弯刚度后，加劲梁竖向位移、弯矩和应力减小。并且随着主缆抗弯刚度的增大，加劲梁静力响应逐渐减小。在对称荷载作用下，索梁最优刚度比为0.5左右，加劲梁竖向位移和弯矩最大减小30%和70%；在非对称荷载作用下，最优刚度比为0.1左右，加劲梁竖向位移和弯矩最大减小25%和60%。主缆与塔顶鞍座的连接方式和主缆线形对加劲梁位移、内力和应力也有一定的影响。

；悬索桥；主缆；抗弯刚度；主缆线形；参数化建模方法；静力响应

0　引言

悬索桥造型优美，结构受力合理，经济性能良好，施工技术趋于成熟，近些年来得到大力的发展。然而悬索桥属于柔性结构，在外界作用，特别是日益繁重的交通荷载作用下，容易产生较大的变形，影响行车的舒适和安全。为此，工程技术人员采用了各种措施来提高悬索结构的刚度和稳定性。主缆是悬索体系的主要承重构件，其刚度和线形等几何参数直接影响到整个体系的受力分配和变形。目前针对悬索桥的分析中，一般假定主缆为理想柔性，只能承受轴向拉力，忽略其抗弯刚度。对于小跨径悬索桥，主缆截面较小，抗弯刚度小，对桥梁受力性能几乎没有影响，将其视为理想柔性是合理的。然而随着悬索桥跨度的不断增大，主缆截面也越来越大，忽略其抗弯刚度，将会对结构的受力分析产生偏差，使桥梁设计偏于保守，造成经济上的浪费[1-5]。同时主缆抗弯刚度在丝股架设过程中、紧缆和安装索夹后、加劲梁吊装过程中以及成桥后的不同阶段，其参数在不断变化[1]。因此有必要对主缆的抗弯刚度及其参数变化对桥梁受力性能的影响规律展开研究。本文基于一个简化的悬索桥模型，采用有限元参数化分析方法，考虑不同主缆刚度和线形、不同边界条件(主缆铰接或固结)以及不同荷载形式，对悬索桥的挠度和内力进行了对比分析，得到了一些结论，可为悬索桥的设计提供参考。

1　基本计算理论

一般的主缆线形计算理论是在主缆是理想柔性、无抗弯刚度这一基本假定的基础上进行的，但随着缆索结构跨度的增大，该类型理论的适用范围开始逐渐受到限制。不考虑抗弯刚度即理想索情况下，主缆为抛物线，曲线方程为：

由平行钢丝组成的悬索桥主缆构件存在实际抗弯刚度，考虑抗弯刚度后，理论的仅受拉柔性缆索结构即变为劲性缆索结构。主缆微段受力如图1所示。

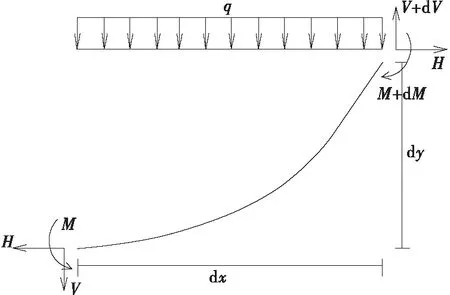
图1　主缆微段受力示意图

(1)

(2)

(3)

式(3)中系数的大小可由边界条件确定。假定梁段固结，则端部的边界条件可表示为：

(4)

把式(4)代入式(3)，可得：

(5)

对悬索桥进行考虑主缆抗弯刚度的受力计算时，由于该类桥梁结构体系并未发生变化，其成桥状态下的内力计算依然可以根据现有理论，首先将加劲梁视为多点支撑的多次超静定结构，采用刚性支承连续梁法并结合结构力学的基本力法方程初步拟定。然后结合有限元软件建立全桥模型，利用类似于不考虑主缆抗弯刚度工况下的悬索桥分析控制选项，根据实际边界条件及目标线形设定主缆的垂点组与更新节点组，重新求解得到全桥成桥之后的平衡状态[3]。

2　有限元模型

利用有限元软件ANSYS，采用参数化建模方法，对一悬索桥进行了模拟。模型1中不考虑主缆的抗弯刚度，主缆和吊索采用杆单元Link10模拟，加劲梁和主塔采用梁单元Beam4模拟；模型2中考虑主缆的抗弯刚度，因此主缆、加劲梁和主塔均采用梁单元Beam4模拟，吊索采用杆单元Link10模拟。主缆与塔顶鞍座采用铰接或固结两种方式。两模型中均考虑主缆的几何非线性。材料参数为：弹性模量E=2.1×105MPa，泊松比v=0.3。图2为全桥有限元模型，图3为该桥的基本结构体系。表1为悬索桥主缆和加劲梁的几何参数，表2为荷载参数。

图2　全桥有限元模型

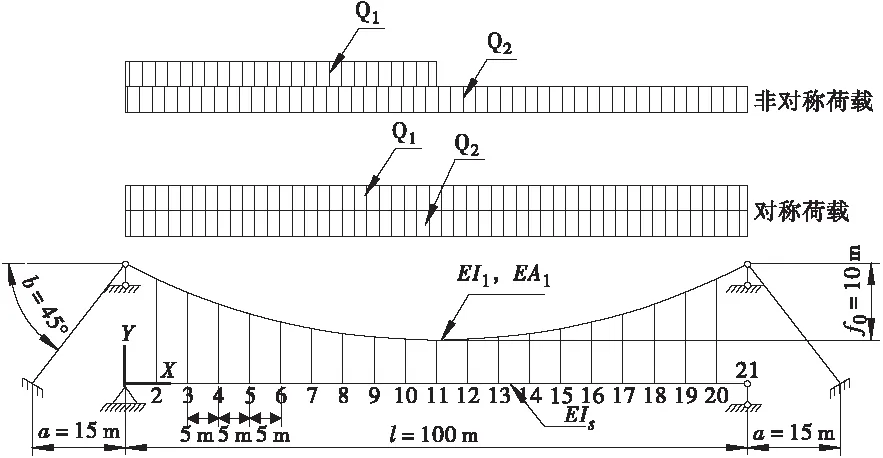
图3　结构基本体系和布载方式

表1 悬索桥主缆和加劲梁的几何参数刚度比ζ=EIc/EIg主缆抗弯刚度EIc/(kN·m2)加劲梁刚度EIg/(kN·m2)00460110080000.14766976000460110080000.27933888000398216320000.413202944000328460160000.617512128000290503680000.8199751680002442540800012173760000021271936000

表2 荷载参数γ=Q1/Q2活载Q1/(kN·m-2)恒载Q2/(kN·m-2)1.05.05.01.55.03.332.05.02.52.55.02.03.05.01.66

3　结果分析

主缆是悬索桥的主要承重构件，是几何可变体，主要承受张力。主缆不仅可通过自身弹性变形，而且可以通过几何形状的改变来影响体系平衡。加劲梁是悬索桥保证车辆行驶、提供结构刚度的二次结构，只要承受弯曲内力，并且其弯曲内力主要来自二期恒载和活载。通过对比分析不同索梁刚度比和静活载比下结构位移、弯矩和应力，找出主缆抗弯刚度对悬索桥结构性能的影响及其变化规律。

3.1对称荷载

悬索桥在对称荷载作用下的计算结果如图4～图7所示。其中，图4为不同索梁刚度比下加劲梁竖向位移曲线，图5为两种边界条件下加劲梁跨中挠度变化曲线，图6、图7为跨中加劲梁和主缆弯矩、应力变化曲线。

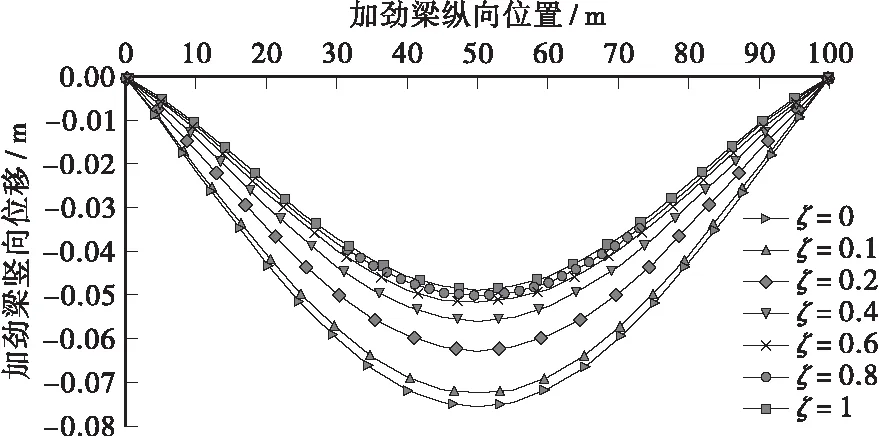
图4　加劲梁竖向位移

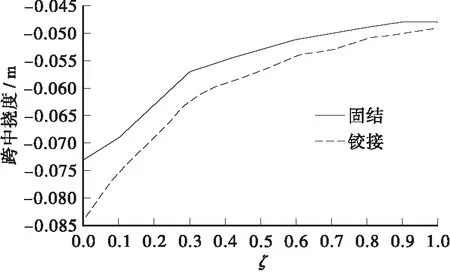
图5　加劲梁跨中挠度变化曲线

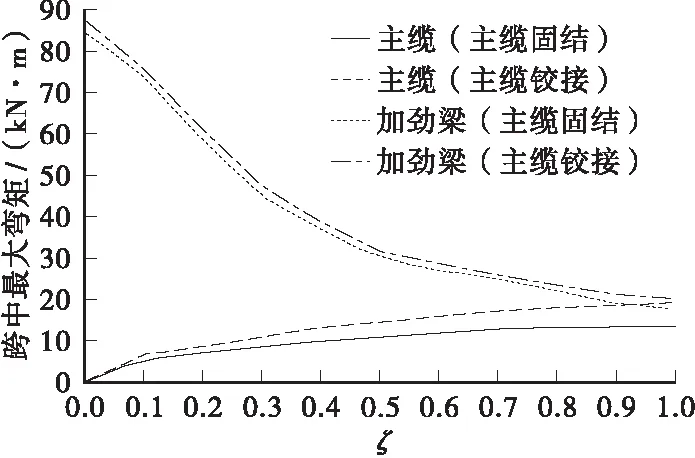
图6　加劲梁和主缆跨中弯矩

图7　加劲梁和主缆跨中应力

从图4中可以看出，考虑主缆抗弯刚度后，加劲梁竖向位移、弯矩和应力减小，这是由于主缆作为悬索体系的一部分参与受弯。并且随着索梁刚度比的增大，减小的越多，但并不是呈线性变化。从图5和图6可以看出，当索梁刚度比ζ从0增大到0.5时，加劲梁跨中挠度和弯矩分别减小了30%和70%左右，而当ζ从0.5增大到1时，跨中挠度和弯矩只下降了10%和15%。可以得到，主缆最优抗弯刚度应取为加劲梁刚度的一半。从图6和图7可以看出，虽然主缆弯矩和弯曲应力也随着ζ的增大而增大，但是增大的幅度很小，主缆弯曲应力最大增加9%，主缆仍主要承受轴力作用。从图5和图6中还可以看出，在主缆铰接和固结两种不同边界条件下，加劲梁位移和内力变化趋势基本一致。主缆固结时加劲梁位移和弯矩比主缆铰接时小，最大减小10%左右，说明主缆固结对加劲梁受力有利。

3.2非对称荷载

悬索桥在非对称荷载作用下的计算结果如图8～图12所示。图8为不同索梁刚度比下加劲梁竖向位移曲线，图9为加劲梁L/4处和3L/4处挠度变化曲线，图10、图11分别为L/4处加劲梁和主缆弯矩、应力变化曲线，图12为不同边界条件下加劲梁和主缆最大弯矩变化曲线。

图8　加劲梁竖向位移

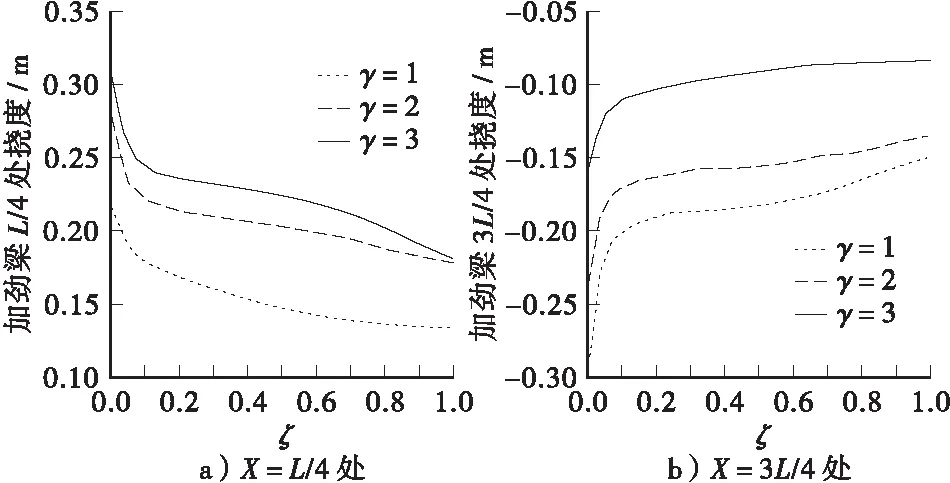
图9　加劲梁挠度随ζ变化曲线

图10　加劲梁弯矩随ζ变化曲线

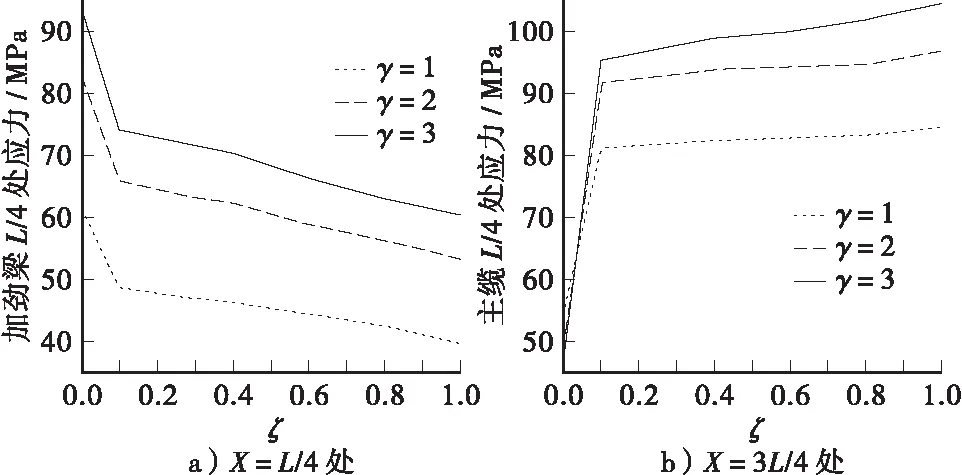
图11　加劲梁应力随ζ变化曲线

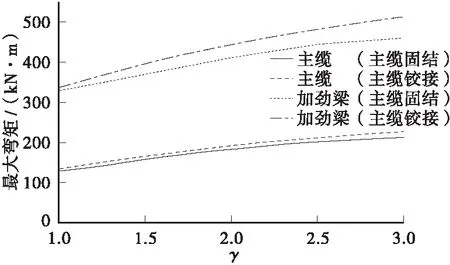
图12　加劲梁和主缆最大弯矩

从图8可以看出，在非对称荷载作用下，加劲梁竖向位移呈S形，并且随着索梁刚度比的增大，位移逐渐减小，曲线趋于平缓。从图9可以看出加劲梁最大挠度随着ζ的增大而减小。当ζ位于0～0.1之间时，挠度减小较快，ζ=0.1时，加劲梁向上的挠度减小了25%，向下的挠度减小了60%。但是当ζ继续增大时，挠度较小变慢，ζ从0.2增大到1是，挠度最大只减小10%左右。从图10、图11可以看出加劲梁最大弯矩和应力随ζ的变化规律与图8相似，主缆弯矩和应力随ζ的增大而增大。从图12可以看出，主缆固结时加劲梁和主缆最大应力要比主缆铰接时小。从图8～图12，加劲梁和主缆位移、弯矩和应力随着静活载比的增大而增大。

4　主缆线形的影响

悬索桥主缆、主塔和加劲肋共同承受荷载作用，受力按刚度分配。主缆作为主要受力构件，是几何可变体，可以通过改变成桥状态的主缆几何线形来影响体系平衡状态，直接影响结构整体受力分配。在施工工序及荷载不变的情况下，主缆成桥线形与主缆空缆状态的线形有关。图13为模型所采用的5种主缆空缆线形，图14为不同主缆空缆线形下加劲梁的位移曲线。从图中可以看出，在对称荷载作用下，主缆空缆线形采用抛物线时，加劲梁位移最小；采用直线时，加劲梁位移最大。在非对称荷载作用下，主缆空缆线形采用抛物线时，加劲梁向下的位移最小，向上的位移最大；采用直线时，向下位移最大，向上位移最小，通过改变主缆形状可以减小甚至消除加劲梁向上的位移。

从式(5)可以看出，主缆的抗弯刚度对主缆的线性有一定程度的影响，以前对于主缆线形的研

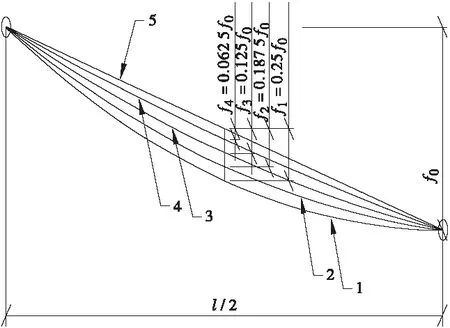
图13　主缆线形

图14　加劲梁竖向位移

究多是基于主缆理想柔性，因此后续有必要对考虑主缆抗弯刚度后主缆线形对结构受力的影响进行分析。

5　结论

本文针对某悬索桥，采用有限元参数化建模方法对其进行了模拟，模型中考虑了主缆与塔顶鞍座连接方式、不同荷载形式和不同主缆初始线形等因素，分析了主缆抗弯刚度对悬索桥加劲梁和主缆位移、内力和应力的影响。结果表明，考虑主缆抗弯刚度后，加劲梁竖向位移、弯矩和应力减小，主缆承受部分弯矩，但加劲梁仍是主要受弯构件，主缆仍主要承受轴力作用。随着主缆抗弯刚度的增大，加劲梁静力响应减小。在对称荷载作用下，索梁最优刚度比为0.5左右，加劲梁竖向位移和弯矩最大减小30%和70%；在非对称荷载作用下，最优刚度比为0.1左右，加劲梁竖向位移和弯矩最大减小25%和60%。主缆与塔顶鞍座的连接方式和主缆线形对加劲梁位移、内力和应力也有一定的影响。

[1]严琨，沈锐利，唐茂林.大跨度悬索桥主缆抗弯刚度模型试验[J].建筑科学与工程学报，2010，27(3)：33-37.

[2]陈国红，刘文，宋晓莉，等.某悬索桥索夹空间受力分析[J].世界桥梁，2015，43(5)：58-62.

[3]刘建，秦祖品，柯红军.考虑主缆抗弯刚度的自锚式悬索桥成桥状态力学性能分析[J].公路与汽运，2015(5)：138-141.

[4]曲婷，王焕定，曾森，等.考虑主缆弯曲刚度后对悬索桥的影响[J].低温建筑材料技术，2009，31(7)：20-24.

[5]罗喜恒，肖汝诚，项海帆.用于悬索桥非线性分析的鞍座-索单元[J].土木工程学报，2005，38(6)：47-53.

[6]刘钊，刘厚军.悬索桥主缆变形及重力刚度新算法[J].工程力学，2009，26(6)：127-132.

[7]郑凯峰，胥润东，栗怀广.悬索桥中央扣对活载挠度影响的详细计算方法[J].世界桥梁，2009(2)：51-53.

[8]江南，沈锐利.矢跨比对悬索桥结构刚度的影响[J].土木工程学报，2013，46(7)：90-97.

[9]张志国，邹振祝，赵玉成.确定悬索桥主缆成桥线形的参数方程法[J].计算力学学报，2005，22(3)：305-309.

2016-04-25

田海龙(1976-)，男，工程师，主要从事公路与桥梁工作。

；1008-844X(2016)03-0108-04

；U 448.25

；A