不同规范下钢管混凝土徐变效应的对比分析

刘少天，徐　岳，朱谊彪

(长安大学 公路学院，陕西 西安　710064)



不同规范下钢管混凝土徐变效应的对比分析

刘少天，徐岳，朱谊彪

(长安大学 公路学院，陕西 西安710064)

JTG D65-2015首次提出钢管内混凝土的徐变模式，通过与常用的ACI 209R-92和CEB-FIP(1990)徐变模式进行比较，运用有限元软件计算了某钢管混凝土拱桥在这3种徐变模式下的徐变效应，对拱肋的应力和变形进行了对比分析。分析表明，JTG D65-2015的计算结果与ACI 209R-92和CEB-FIP(1990)相比，拱肋的应力和挠度都降低了30%左右。结果可供同类工程参考。

；钢管混凝土拱桥；徐变效应；JTG D65-2015；ACI 209R-92；CEB-FIP(1990)

0　引言

钢管混凝土拱桥具有自重轻、强度高、延性好、施工便捷、桥型美观、经济性好等优点。随着现代高性能混凝土的不断发展和现代混凝土泵送技术的广泛应用，钢管混凝土因所具有的抗压承载力高、钢管混凝土拱肋可兼做施工骨架的突出优点，正在被越来越多地应用到拱桥中。

大量工程实践表明，管内核心混凝土处于密闭养护状态，核心混凝土的收缩徐变特性与普通混凝土有着较大的不同。目前的研究结果表明，管内混凝土的收缩、徐变量均小于普通混凝土，但不同研究成果推荐的徐变系数计算方法不尽相同[1]。

目前国内外不同的混凝土徐变模式，考虑的因素不尽相同，总体归纳起来，这些模式的数学表达式大致分为3种：一种是将徐变系数表达为一系列系数的乘积，每一系数表示一个影响徐变的重要因素，采用乘积模型的有英国规范ACI 209R(1992)[2]、CEB-FIP(1990)[3]，JTG D62-2004[4]也采用了类似乘积的形式；另一种是将徐变系数表达为若干个性质互异的分项系数之和，采用和模式的有CEB-FIP(1978)和我国的JTJ 023-85规范；还有一种则是采用上述两种的混合形式，如RILEM B3(1995)模型和BP模型。

JTG D65-2015[5]规范第一次提出了钢管混凝土的徐变系数计算公式。为了分析该计算模式与其他混凝土徐变系数计算模式的区别，本文选取了ACI 209R(1992)、CEB-FIP(1990)和JTG D65-2015的徐变模式进行实例工程徐变效应的计算。

1　徐变模式

1.1ACI 209R-92徐变模式

ACI 209R-92模型从混凝土材料对徐变的影响出发，考虑了混凝土的坍落度、养护条件、细骨料含量和拌合物空气含量等多方面因素，采用连乘的形式，公式直接体现徐变的影响参数，简单明了，并且可以区分计算普通混凝土与泵送混凝土的徐变。

1.1.1计算公式

钢管混凝土结构中管内混凝土的徐变模式采用双曲线函数，考虑影响混凝土徐变终值系数的各种因素，同时不区分弹性变形和塑性变形，混凝土的徐变系数φ(t，τ)可按下列规定计算[6]：

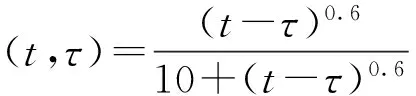
(1)

式中：t为混凝土徐变系数计算时间；τ为混凝土加载龄期；φ(∞，τ)为徐变系数终值，φ(∞，τ)=2.35·γla·γλ·γh·γVS·γS·γψ·γa，其中标准状态下的徐变系数终值为2.35，γla……γa为偏离标准状态时的校正系数。

1.1.2徐变影响参数

C40微膨胀混凝土坍落度设计值为200 mm，配合比为：水泥∶水∶黄砂∶碎石∶减水剂∶膨胀剂=442∶194∶743∶954∶3.928∶49.1。由混凝土配合比计算得到混凝土砂率44%，混凝土水泥用量 442 kg/m3。在Midas civil中输入相应参数得到的徐变系数曲线如图1所示。

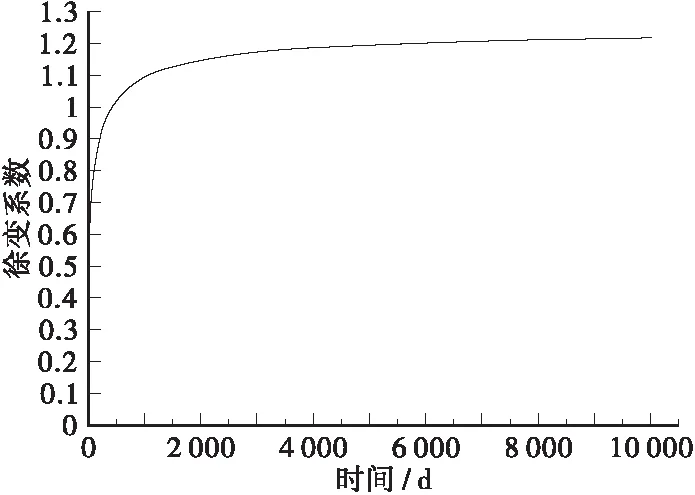
图1　ACI 209R-92徐变系数曲线

1.2CEB-FIP(1990)徐变模式

CEB-FIP(1990)模型采用一个双曲幂函数来描述徐变系数随时间的变化规律，其用一个名义徐变系数来表示环境相对湿度、构件理论厚度、混凝土强度、加载龄期等参数变化对徐变系数的影响，但是该模型不能体现混凝土某些工作性能改变对徐变的影响。

1.2.1计算公式

CEB-FIP(1990)模式没有具体区分各类徐变，公式表达采用连乘的形式，将徐变系数随时间的变化规律拟合为双曲幂函数，通过3个修正系数与其相乘得到混凝土徐变系数的表达式为：

φ(t，t0)=φ(∞，t0)·βc(t-t0)

(2)

φ(∞，t0)=β(fc)·β(t0)·φRH

(3)

(4)

(5)

(6)

式中：β(fc)为取决于混凝土抗压强度fc的参数；β(t0)为取决于加载龄期t0的参数；φRH为取决于环境相对湿度的参数。

徐变随时间发展的系数βc(t-t0)为：

(7)

式中：βH取决于相对湿度和构件尺寸，表达式为：

(8)

1.2.2徐变影响参数

CEB-FIP(1990)计算模式的影响参数主要有混凝土抗压强度标准值fck、外部环境相对湿度值RH、构件理论厚度、水泥类型和收缩时混凝土龄期等。在Midas civil中输入相应参数得到的徐变系数曲线如图2所示。

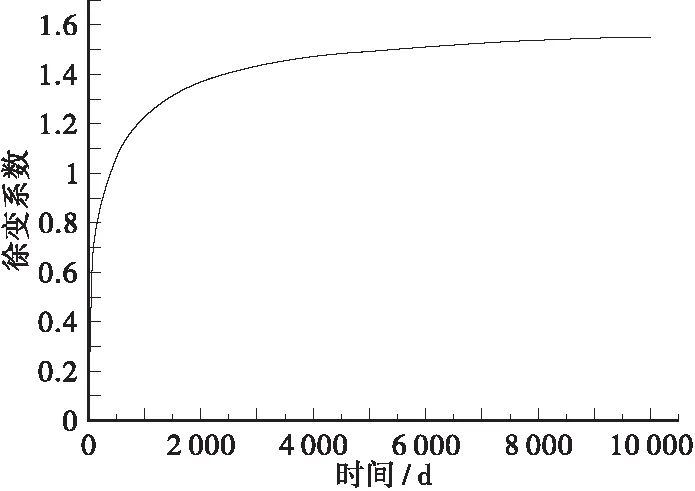
图2　CEB-FIP(1990)徐变系数曲线

1.3JTG D65-2015徐变模式

1.3.1计算公式

钢管混凝土的徐变系数可按下列公式计算：

(9)

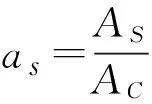
1.3.2徐变影响参数

由于Midas civil中没有JTG D65-2015的徐变系数模式，通过在软件中输入JTG D62-2004规定公式影响参数，根据得到的徐变系数坐标值，并按照给出的徐变系数公式计算出JTG D65-2015的徐变系数坐标值。将得到的坐标值输入自定义徐变系数坐标中，得出徐变系数曲线。根据计算结果得出的徐变系数曲线如图3所示。

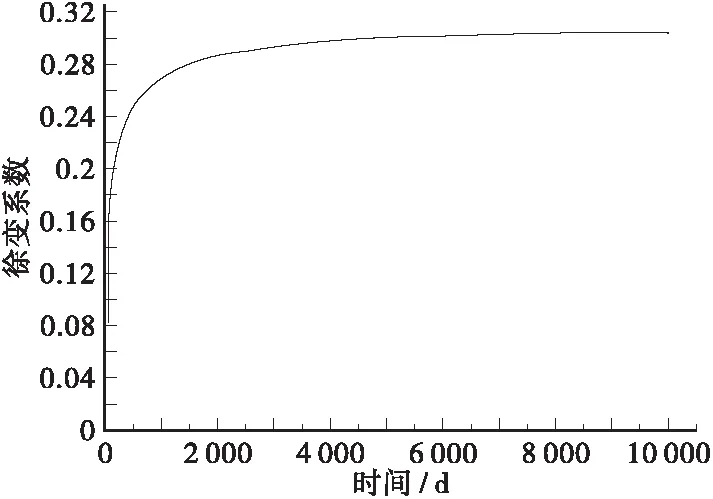
图3　JTG D65-2015徐变系数曲线

2　实桥分析

2.1模型建立

依托工程为一下承式钢管混凝土系杆拱桥，计算跨径96 m，计算矢高19.2 m，拱轴线为二次抛物线；拱肋采用哑铃型钢管混凝土，拱肋高2.4 m，钢管外径1.0 m，壁厚14 mm，管内填充C40微膨胀混凝土，腹腔中不填充；沿纵桥向每5 m设一吊杆，共16根，采用低应力防腐拉索；拱肋间设5道一字型钢管风撑及2道K字风撑，钢管壁厚为14 mm；系梁采用箱形截面，每一片系梁内布设12束15-9钢绞线和2束15-10钢绞线；行车道板采用25 cm高实心板。Midas civil建模如图4所示。

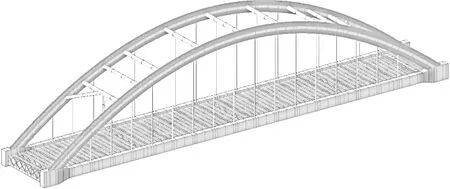
图4　实桥模型图

2.2计算结果及分析

针对依托工程，通过有限元软件建模计算，可以得到3种徐变模式下成桥3 a钢管混凝土拱肋的应力和变形数据。

2.2.1应力分析

拱肋(包括钢管和钢管内混凝土)应力计算结果见表1。

由表1中的计算结果可知：

1) ACI 209R-92计算结果最大，钢管应力最值之差约39.4%，上钢管混凝土最值之差约20.6%，下钢管混凝土最值之差约53.5%。

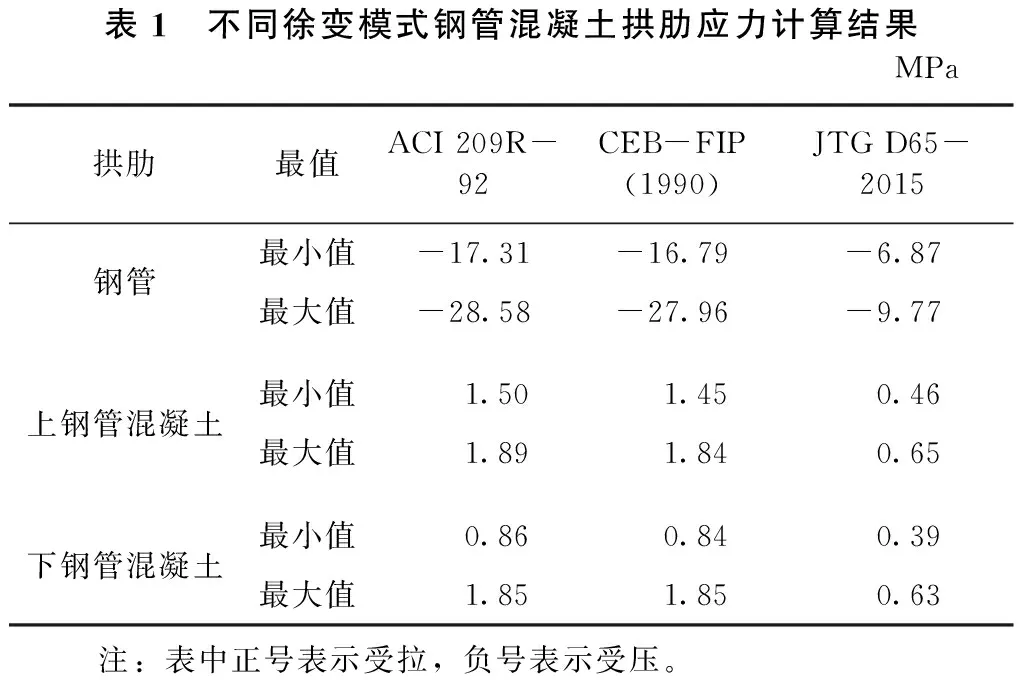
表1 不同徐变模式钢管混凝土拱肋应力计算结果MPa拱肋最值ACI209R-92CEB-FIP(1990)JTGD65-2015钢管最小值-17.31-16.79-6.87最大值-28.58-27.96-9.77上钢管混凝土最小值1.501.450.46最大值1.891.840.65下钢管混凝土最小值0.860.840.39最大值1.851.850.63 注:表中正号表示受拉,负号表示受压。

2) CEB-FIP(1990)计算结果次之，钢管应力最值之差约39.9%，上钢管混凝土最值之差约21.2%，下钢管混凝土最值之差约54.6%。

3) JTG D65-2015计算结果最小，钢管应力最值之差约29.7%，上钢管混凝土最值之差约29.2%，下钢管混凝土最值之差约38.1%。

4) ACI 209R-92与CEB-FIP(1990)计算结果较为接近，远大于JTG D65-2015的计算结果，JTG D65-2015的结果约为ACI 209R-92与CEB-FIP(1990)结果的1/3左右。

2.2.2变形

从施工完毕到成桥3 a，以30 d为时间间隔，对不同徐变模式下拱肋跨中截面竖向挠度的变化进行分析，挠度变化结果见图5。

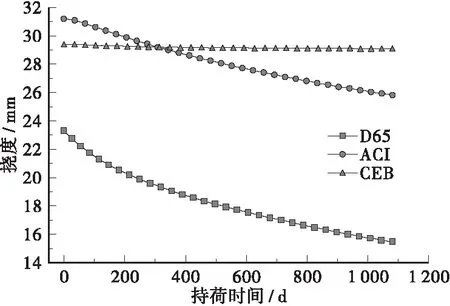
图5　拱顶挠度曲线

由图5可知：

1) ACI 209R-92与CEB-FIP(1990)挠度较为接近，JTG D65-2015挠度则差别较大，大概为其它两个挠度值的1/3左右。

2) CEB-FIP(1990)挠度基本不变，ACI 209R-92与JTG D65-2015挠度都在逐渐减少，且减少的趋势和幅度较为接近，大概为33%左右。

3　结论

本文基于3种不同的徐变模式，依据实桥工程，通过有限元计算软件对钢管混凝土拱桥拱肋的应力和变形进行了对比分析，分析表明JTG D65-2015的计算结果与ACI 209R-92和CEB-FIP(1990)相比，由徐变作用产生的应力是ACI的40%左右，是CEB的41%左右；拱顶挠度是ACI和CEB的33%左右。JTG D65-2015徐变模式的可行性还有待随实际工程中相关数据的积累作进一步研究。

[1]王元丰.钢管混凝土徐变(精)[M].北京：科学出版社，2006.

[2]ACI Committee 209.Prediction of creep，shrinkage and temperature effects in concrete structures[R].Detroit：ACI SP27-3，1992.

[3]欧洲-国基混凝土委员会，中国建筑科学研究院结构所规范室译.1990CEB-FIP模式规范(混凝土结构)[Z].1991.

[4]JTG D62-2004，公路钢筋混凝土及预应力混凝土桥涵设计规范[S].

[5]JTG-T D65-06-2015，公路钢管混凝土拱桥设计规范[S].

[6]赖秀英，陈宝春.钢管混凝土拱桥徐变系数模型对比分析[J].福州大学学报(自然科学版)，2014(5)：737-743.

[7]李生勇，李凤芹，陈宝春，等.钢管混凝土拱桥徐变影响分析[J].铁道学报，2011，33(3)：100-107.

[8]韩冰，杜金生，王元丰.徐变对钢管混凝土拱桥的影响分析[J].公路交通科技，2005，22(6)：75-77.

[9]顾建中，刘西拉，陈卫峰.考虑徐变的钢管混凝土拱桥结构分析[J].上海交通大学学报，2001，35(10)：1574-1577.

[10]彭建新，邵旭东，程翔云，等.钢管混凝土拱肋徐变研究[J].工程力学，2007，24(6)：79-85.

[11]曾彦.钢管混凝土徐变研究发展概述[J].公路交通技术，2005(2)：73-75.

[12]李生勇.钢管混凝土拱桥结构徐变研究[D].福州：福州大学，2010.

[13]陈宝春.钢管混凝土拱桥(第2版)[M].北京：人民交通出版社，2007.

[14]谢肖礼，秦荣.收缩徐变对钢管混凝土拱桥影响的理论研究[J].桥梁建设，2001(4)：1-4.

2016-01-18

刘少天(1992-)，男，在读研究生，研究方向：桥梁结构。

；1008-844X(2016)03-0094-04

；U 441

；B