路堑边坡降雨入渗对路基渗沟渗流量影响分析

郭　鑫，李志勇

(1.长沙理工大学 交通运输工程学院，湖南 长沙　410114；2.湖南省交通科学研究院，湖南 长沙　410015)



路堑边坡降雨入渗对路基渗沟渗流量影响分析

郭鑫1，李志勇2

(1.长沙理工大学 交通运输工程学院，湖南 长沙410114；2.湖南省交通科学研究院，湖南 长沙410015)

以路堑边坡工程为例，采用非饱和土理论和有限单元法分析降雨入渗对渗沟流量的影响。研究过程中选取两类土分别模拟3种典型渗沟在4种降雨条件下渗流量的变化规律，并与公式法和饱和流有限单元法计算结果进行比较分析。研究表明：当渗沟沟底设在不透水层上或不透水层坡度较陡时公式法所得结果与饱和-非饱和流有限单元法结果相比偏小，当沟底距不透水层较远时公式法所得结果偏大；短时间降雨对渗流量基本无影响，长时间降雨对渗流量有明显的影响，且对浅埋渗沟的影响大于深埋渗沟。

；路堑；边坡；非饱和土；降雨；渗沟；渗流量

0　引言

公路路基病害种类很多，如沉陷、冻胀、冲刷以及沼泽化等，形成病害的原因也很复杂，但水的作用是主要因素之一。影响路基稳定的水主要有两个来源：地下水和降雨。地下水的水位变化对路基土的弯沉和回弹模量有很大的影响，通过弯沉和回弹模量的变化进而对路面各层应力分布产生影响。降雨除了对边坡稳定性产生影响外，还会通过渗流的方式从边坡入渗至路基，影响路基内地下水的渗流。

在我国现行的《公路排水设计规范》[1](以下简称《规范》)中，在路基排水方面提供了很多成熟的方法，其中渗沟是目前高速公路建设中用于处理路基内部排水问题的主要设施。在《规范》中将渗沟分为3类：沟底设置在不透水层上的渗沟、沟底距不透水层较远的渗沟和不透水层横向坡度较陡的渗沟。但《规范》中给出的计算公式是基于饱和土渗流理论推导出来的。近几年，随着非饱和土理论和有限元软件的发展，相关学者对于饱和-非饱和渗流已有大量研究，如：刘建华[2]基于非饱和土理论对渗沟进行分析，认为现行计算方法低估了渗流量；周奇[3]基于非饱和土理论通过SEEP/W软件模拟了道路渗流场，认为渗沟或集水管同排水层共同使用可更好地排除路基水分；刘文华[4]分析了降雨入渗条件下非饱和土路基的含水率和基质吸力的分布规律，认为降雨对路基土有明显影响。

本文基于非饱和土渗流理论，使用SEEP/W软件对路堑边坡降雨入渗进行分析，模拟2种不同埋深的渗沟在4种降雨条件下3种不同形式的渗沟渗流量变化，同时与《规范》中渗流量计算结果以及饱和流有限单元法分析结果进行比较分析。

1　渗流量有限单元法理论

1.1非饱和土理论

Fredlund在对非饱和土应力进行研究时，提出采用2种独立应力状态变量来分析非饱和土的理论应力，这2种应力状态分别是：基质吸力(ua-uw)和净法向应力(σ-ua)，式中：ua表示孔隙气压力；uw表示孔隙水压力；σ表示土体单元法向应力。当(ua-uw)=0时代表此时土体为饱和土。

SEEP/W计算软件是采用1932年Richard推导出的非饱和渗流基本微分方程[5]：

(1)

式中：k(Θ)x、k(Θ)y、k(Θ)z分别表示x轴方向、y轴方向和z轴方向的水力传导率；H表示总水头高度；Q表示流量边界；Θ表示土壤体积含水率；t表示时间。从非饱和渗流基本微分方程可以看出，非饱和土中的渗透系数是一个与土壤体积含水率相关的变量。

1.2有限单元法计算渗流量

有限单元法是将一个分析整体划分为有限个由节点相连接的单元体。在计算时用连续的分片插值函数建立一个个单元方程，再通过节点的连接作用形成代数方程组进行求解[6]。在利用有限单元法计算渗流量时，首先确定渗流场内的水头，其一般方程形式如下：

Kh=f

(2)

式中：K表示渗透矩阵；h表示水头列向量；f表示自由项列向量。

计算饱和-非饱和渗流时，还要确定饱和-非饱和渗流分界面，此时分为稳定渗流和非稳定渗流两种情况：当属于稳定渗流时，分界面上任意一点的水头高度和该点的位置高程相等，即表示压力水头为0；当属于非稳定渗流时，还应计算通过分界面流入饱和区的单宽流量q，计算公式：

(3)

式中：μ表示分界面变动范围内的土体给水度；h*表示分界面上的水头高度；t表示时间；θ表示分界面外法向与垂线的夹角。在计算渗流量时，假设断面A为渗流断面，则通过A断面的渗流量方程为：

(4)

如果某一渗流断面由n个单元组成，则渗流量Q是通过这些单元渗流量的代数和，其方程如下：

(5)

在有限元软件中根据材料参数和初始水位线通过式(1)和式(2)分别计算各节点的渗透系数和水头高度；饱和-非饱和渗流区别于饱和渗流的关键在于在非饱和区同样存在一定的渗流量，即式(3)计算出的由非饱和区流入饱和区的渗流量；最后通过式(4)计算出每个单元的渗流量，再通过式(5)将断面上各单元的渗流量相叠加，最终计算出一个断面的总渗流量。

2　计算模型

利用SEEP/W软件建立路堑边坡模型如图1，并进行饱和-非饱和土模型的数值模拟分析。模拟试验分析南方非冻区渗沟渗流量变化，分别采用2种不同的土体来模拟浅埋渗沟和深埋渗沟，土体1为亚粘土，土体2为风化花岗岩残积土，具体参数见表1。通过查阅相关文献[7]渗沟的构造参数为：高度0.8 m，宽度0.6 m，渗沟内设计水深0.4 m。渗沟采用左右两侧进水，上下两侧不进水的形式。依据《规范》中渗沟埋深计算公式得到浅埋渗沟埋深3.45 m，深埋渗沟埋深6.55 m，水位线位于地基以下1 m的位置。

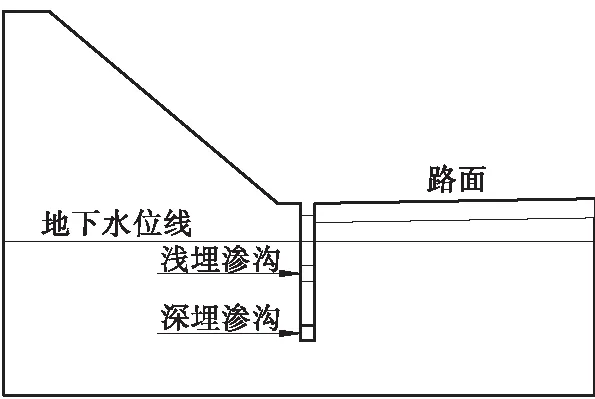
图1　有限元计算基本模型

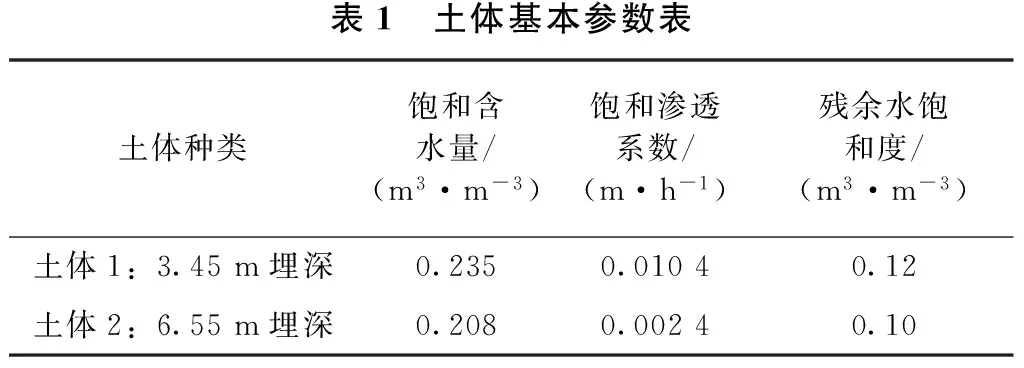
表1 土体基本参数表土体种类饱和含水量/(m3·m-3)饱和渗透系数/(m·h-1)残余水饱和度/(m3·m-3)土体1:3.45m埋深0.2350.01040.12土体2:6.55m埋深0.2080.00240.10

试验分别模拟4种不同的降雨条件；①短时间小降雨0.001 6 m/h，降雨历时8 h；②短时间强降雨0.032 m/h，降雨历时8 h；③长时间小降雨0.001 6 m/h，降雨历时160 h；④长时间强降雨0.002 5 m/h，降雨历时160 h。为了更接近真实情况，在降雨前先进行48 h无降雨自由渗流，路堑边坡为入渗面，路面结构认为是不透水结构。

文中分别采用了3种计算方法：公式法、饱和流有限单元法和饱和-非饱和流有限单元法。为了能够和《规范》公式法计算所得结果相比较，本文采用变换不透水层高度和坡度的形式，分别模拟3种不同形式渗沟在不同降雨条件下的渗流量变化，来分析《规范》中公式法对于不同埋深渗沟的适用性。

3　分析与讨论

3.1渗沟沟底设在不透水层上

表2给出了沟底设在不透水层上时公式法和饱和流有限单元法的计算结果，可以看出这2种方法所得的渗流量基本相同。

表2 沟底设在不透水层上时渗流量计算结果埋深/m公式法/(m3·h-1)饱和流有限元法/(m3·h-1)3.450.0040.0046.550.00440.0042

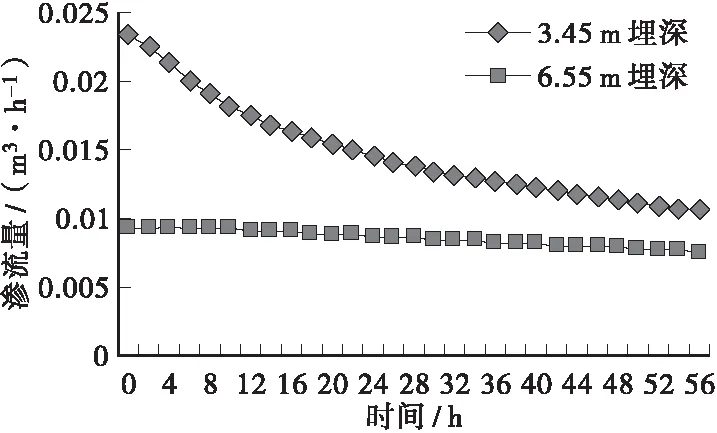
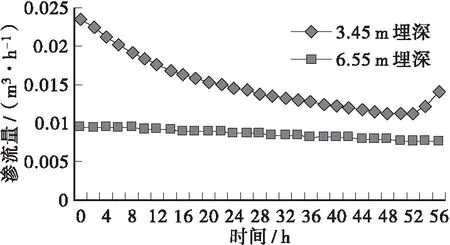
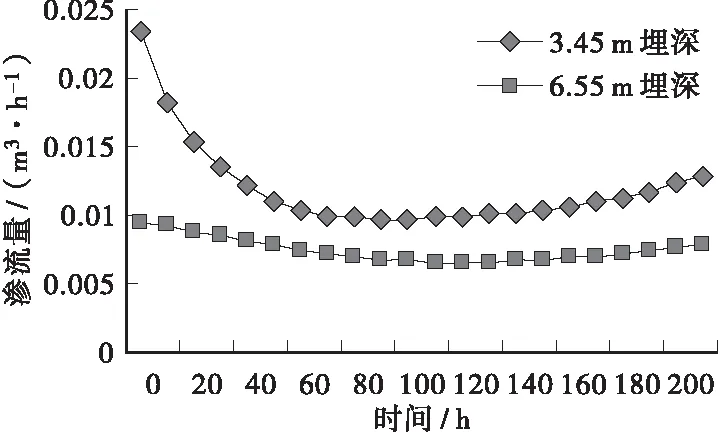
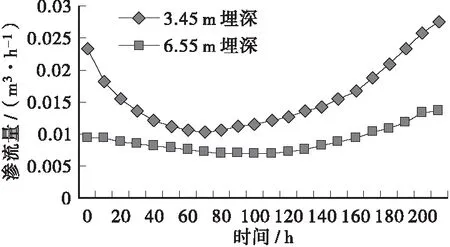
图2～图5分别给出了4种降雨条件下渗流量的变化情况，可以看出：3.45 m埋深的渗沟在短时间降雨条件下均未超过公式法得出的设计流量，在长时间小降雨和长时间强降雨中分别从204 h和144 h时开始超过设计流量；对于6.55 m埋深的渗沟，非饱和土有限元法模拟所得渗流量均超过设计流量。因此，当渗沟沟底设在不透水层上时，公式法对于浅埋渗沟适用性较好；对于深埋渗沟适用性差，计算结果偏低。同时从图中可以看出短时间降雨对渗流量无影响；长时间降雨对渗流量影响显著，随着降雨强度的增加渗流量增加明显，通过渗流量曲率的变化可以发现长时间降雨对于浅埋渗沟的影响高于深埋渗沟。

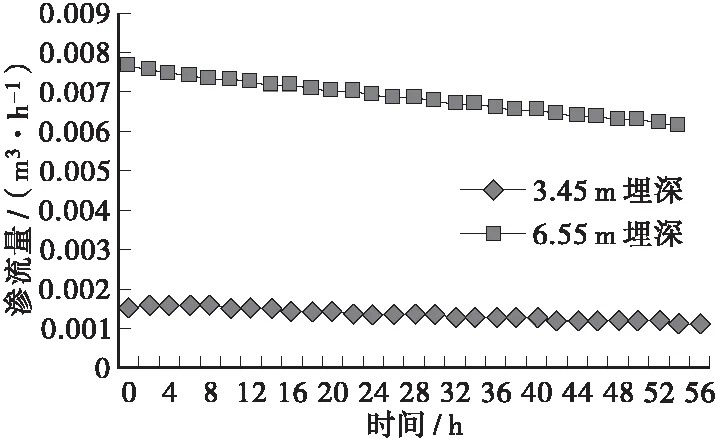
图2　短时间小降雨条件下渗流量变化

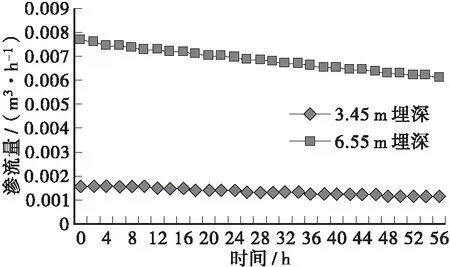
图3　短时间强降雨条件下渗流量变化

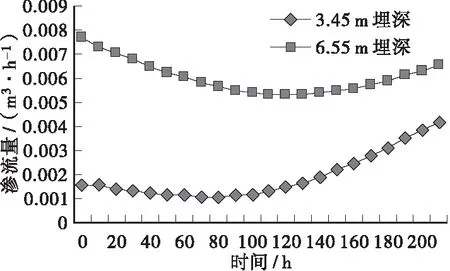
图4　长时间小降雨条件下渗流量变化

图5　长时间强降雨条件下渗流量变化

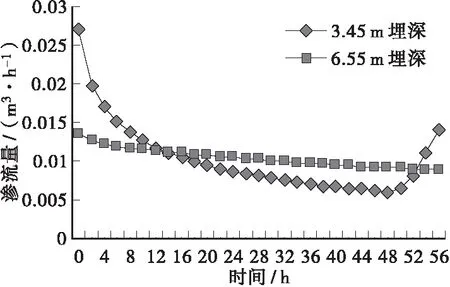
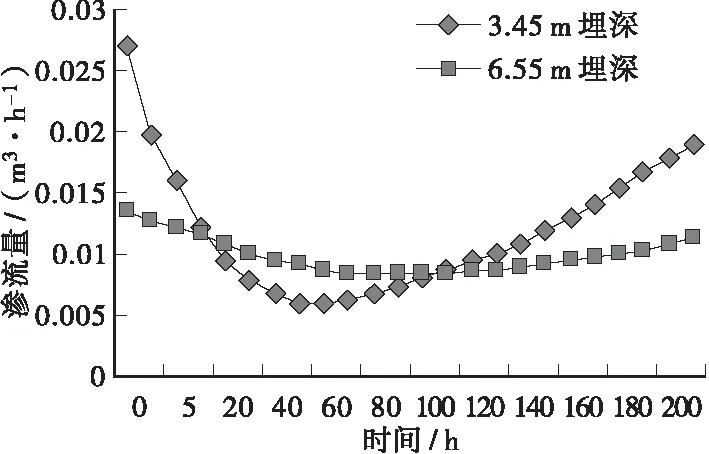
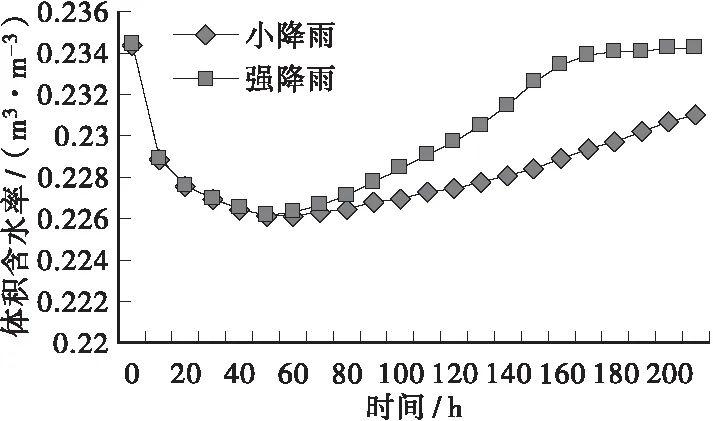
3.2渗沟沟底距不透水层顶面较远

《规范》对于沟底距不透水层顶面较远时给出的计算公式为式(6)，式中：Kh表示含水层材料的渗透系数；hs表示渗沟位置处地下水位的下降幅度；Ls表示地下水位受渗沟影响而降落的水平距离；Ll表示相邻两渗沟间距之半。通过观察计算公式可以发现：当Ll>2Ls时，公式无意义；当2Ls>Ll>Ls时，表示地下水受渗沟影响而降落的水平距离小于两渗沟间距之半，此时认为渗沟实际上对降低地下水位不起作用；只有当Ll

(6)

在分析中，3.45 m埋深的渗沟计算所得Ls=8.42 m，而Ll=12.25 m不符合设计要求，此时常采用的方法是缩小两渗沟之间的间距，因此模拟时将两渗沟间距缩短为16 m，即Ll=8 m。

表3给出了沟底距不透水层较远时公式法和饱和流有限单元法的计算结果，可以看出公式法的计算结果明显高于饱和流有限单元法。根据图6至图9可以看出，无论浅埋还是深埋的渗沟，在4种降雨条件下渗流量均未超过设计值，表明《规范》中给出的计算公式比较保守，安全性高。这与刘晓南[9]通过公式推导得出《规范》中给出的公式计算结果偏高的结论相同。同时从图6和图7可以看出短时间小降雨对渗沟流量基本无影响，短时间强降雨对于浅埋渗沟有一定影响；图8和图9可以看出长时间降雨对渗流量影响明显。

研究表明持力层以下1.8 m是汽车荷载的主要作用区[10]，一般路基路面的总厚度约为1 m，因此在路基底面以下80 cm是主要的荷载作用区，则所选监测点位于距左侧边沟3.25 m(硬路肩与行车道交界处)面层以下1.8 m处。在设计3.45 m埋深渗沟时采用缩小渗沟间距的方法，在长时间降雨条件下监测点处土壤体积含水率变化如图10。

表3 沟底距不透水层顶面较远时渗流量计算结果埋深/m公式法/(m3·h-1)饱和流有限元法/(m3·h-1)3.450.0440.0216.550.04070.012

图6　短时间小降雨条件下渗流量变化

图7　短时间强降雨条件下渗流量变化

图8　长时间小降雨条件下渗流量变化

图9　长时间强降雨条件下渗流量变化

通过观察体积含水率变化发现在长时间降雨的影响下路基土的体积含水率会有明显的回升，在降雨开始前的48 h自由渗流下，监测点处的土壤体积含水率从0.234 m3/m3到0.226 m3/m3，表明渗沟起到了排水作用；但开始降雨后监测点的体积含水率会开始上升，尤其在长时间强降雨的影响下土壤会达到接近饱和的含水率显然不利于持力层正常工作。

图10　监测点处土壤体积含水率变化

3.3不透水层横向坡度较陡

表4给出了不透水层横向坡度较陡时公式法和饱和流有限元法的计算结果，可以看出饱和流有限单元法的计算结果明显高于公式法。

表4 不透水层横向坡度较陡时渗流量计算结果埋深/m公式法/(m3·h-1)饱和流有限元法/(m3·h-1)3.450.00570.0176.550.00360.0053

图11～图14分别给出了不透水层横向坡度较陡时渗流量变化规律。从图中可以看出饱和-非饱和流有限单元法得到的渗流量结果均比公式法和饱和流有限单元法的计算结果大，说明现行的公式法低估了渗流流量。产生这种情况的主要原因是当不透水层横向坡度较陡时渗流水头高度H难以确定。同济大学刘建华博士通过工程实例验证得出了考虑土的非饱和特性所得到的流量值与实际流量更为接近的结论[11]。同时从图中也可以看出只有在长时间强降雨条件下渗流量有显著影响，其余3种降雨条件影响程度较低。

图11　短时间小降雨条件下渗流量变化

图12　短时间强降雨条件下渗流量变化

图13　长时间小降雨条件下渗流量变化

图14　长时间强降雨条件下渗流量变化

4　结论

1) 饱和-非饱和流有限单元法计算得到的结果与现行公式法求得的结果存在一定差别。其中：

当渗沟沟底设在不透水层上时公式法所得结果适用于浅埋渗沟，对于深埋渗沟计算结果偏小；当渗沟沟底距不透水层较远时公式法求解适用性好，所得结果高于饱和-非饱和流有限元法所得值，即便在长时间强降雨条件下渗流量也未超过公式法给出的设计流量；当不透水层横向坡度较陡时公式法计算出的渗流量与饱和-非饱和流有限单元法相比明显偏小。

2) 短时间降雨对于渗流量的影响可以忽略；长时间降雨对于渗流量影响大，尤其对浅埋渗沟影响明显，随着降雨强度的增加，渗流量上升越明显。南方地区夏季常出现持续天阴有雨的气候现象，因此在设计沟底设在不透水层上和不透水层坡度较陡这两种情况的渗沟的流量时，应根据气象资料考虑长时间降雨对渗流量的影响。

3) 在计算沟底距不透水层较远的渗沟渗流量时，如果不符合Ll

[1]JTG/TD33-2012，公路排水设计规范[S].

[2]刘建华.公路地下排水设计理论与土工合成材料应用研究[D].上海：同济大学交通运输工程学院，2005.

[3]周奇.SEEP/W在基于非饱和土理论的公路排水设计计算中的应用[J].中外公路，2009，29(6)：42-46.

[4]刘文华.降雨入渗条件下非饱和土路基渗流分析[J].中外公路，2013，33(2)：15-18.

[5]苑莲菊，李振栓，武胜忠，等.工程渗流力学及应用[M].北京：中国建材工业出版社，2001.

[6]顾慰慈.渗流计算原理及应用[M].北京：中国建材工业出版社，2000.

[7]邓学钧.路基路面工程[M].北京：人民交通出版社，2008.

[8]李志勇，王江帅，李彦伟，等.道路防排水技术[M].北京：人民交通出版社，2011.

[9]刘晓南，杜雨，宋应臬.对现行公路渗沟计算方法若干问题的思考[J].交通科技，2005(3)：15-18.

[10]刘丽萍.黄土沟壑区公路渗沟埋深计算方法[J].中外公路，2010，30(4)：61-64.

[11]刘建华，郭忠印.基于非饱和土理论的公路排水设计方法[J].同济大学学报(自然科学版)，2006，34(2)：191-195.

2016-01-08

郭鑫(1992-)，男，硕士研究生，主要从事道路防排水研究。

；1008-844X(2016)03-0001-05

；U 416.1+3

；A