配电网重构的凸模型
荣德生,胡举爽
(辽宁工程技术大学电气与控制工程学院,葫芦岛125105)
配电网重构的凸模型
荣德生,胡举爽
(辽宁工程技术大学电气与控制工程学院,葫芦岛125105)
推导出了配电网重构的混合整数二次规划模型、二次规划二次约束模型和二阶锥规划模型,并提出有连续凸松弛的AC潮流问题。所提各模型可由标准商业软件可靠、有效地解决最优性问题。在推导各模型的过程中,得到了放射性网络潮流的近似原始二次约束模型和二阶锥规划模型。
配电网重构;负载平衡;混合整数二次规划;二阶锥规划
引言
配电网重构需要合理选择开关的开、闭组合,优化某些性能,同时保持网络的放射性[1-2]。配电网重构最初由支路交换法处理,随后由遗传算法、模拟退火算法和其他一些启发式算法处理[3-6]。由于其广泛适用性,这些方法很受欢迎,比如在黑盒模型中,但是反过来有可能忽略在更大的问题中比较重要的内在结构问题。为此,本文推导出了配电网重构的混合整数二次规划QP (quadratic programming)、二次约束二次规划QCP (quadratically constrained programming)、二阶锥规划SOCP(second-order cone programming)。
当所有变量都连续时,所有此类问题总是凸的,而且可以在多项式时间内高效求解。众所周知,当这类问题中的部分变量是离散变量时,这类问题变成非确定多项式时间难(NP-hard)问题。然而,很多整数规划算法,像分支定界算法,在可以有效地计算边界时能够保持优良性能。因此,希望混合整数问题有凸的,多项式时间连续的松弛。文献[7]中,使用Benders分解法解决了混合整数非线性规划,同理,本文解决了混合整数非线性凸规划。
本文介绍了3种新的凸模型,第3部分展示了它们的实用性。同时,在推导这些公式的过程中,获得了放射式网络的近似潮流公式。该模型代表了AC潮流问题的凸近似,是一种已经在最优潮流、输电规划和机组组合取得成功的方法。本文公式的应用已经超出配电网重构,扩展到许多放射性网络的优化问题,如储能装置配置和分布式发电。
有两点能区分现有方法和本文方法的不同。第一是方便,该模型可以使用许多强大的商业软件解决,让用户只对模型编程而规避算法。虽然标准软件中有许多可调参数,但是默认设置和自动参数选择通常会使算法性能更强大,而且无需用户干预。同样,起始点可以由用户设定,但是如果没有设定,就会自动生成;第二该算法可以保证全局最优,好多启发式算法无法真正地保证全局最优。如结果部分所示,这些解决方案可能确实需要大量的计算时间,然后提供有用的基本解决方案,可作为快速、实时技术的起始解。
1 DistFlow方程
对放射式AC网络,广泛地利用DistFlow方程。pij和qij表示节点i注入节点j的有功功率和无功功率,Vi表示电压幅值,和表示节点i的有功和无功负荷。注意pij和qij不等于pji和qji。由于Vi没有在公式中出现,把v2i本身作为一个变量。B为节点集合,W为线路集合,rij和xij为线路电阻和电抗,除非另有说明,单下表约束都是B矩阵中节点i的约束,双下表约束是W矩阵中节点(i,j)的约束。DistFlow方程为
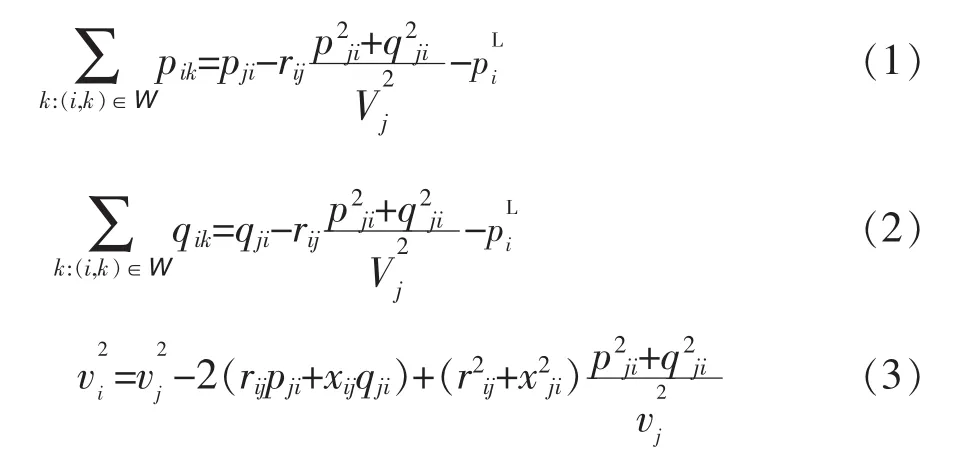
2 凸模型
2.1二次规划
本文使用去除所有二次项约束、与固定电压幅值在同一标幺值下得到的简化DistFlow方程。Ws为W中有开关的线路集合,BF为变电站节点集合。为变电站节点的有功功率和无功功率,M是一个足够大的分离参数。需要注意的是集合BF可以包含多个变电站节点,这些变电站节点连接到一个树上。通过耦合目标,得到混合整数二次规划网损最小的目标函数,即

把式(7)~式(16)作为Ω。连续变量zij和zji指出潮流流动方向的线路有关。每一条开关线路和二进制变量yij有关,当开关打开时是0,闭合时是1。需要注意的是,由于此变量无方向性,因此,二进制变量的个数就等于开关的数量。由此,尽管zij只取0或1,没有必要强制它们是离散的,因此它们的计算量较小。这些放射式约束和文献[7]几乎相同。然而,本文提法更有一般性,因为并不是每条线路都需要开关,这样就潜在地节约了计算时间。为了彻底考虑本文和之前放射式约束提法的不同,将证明本文方案的结果总是放射式重构,首先给出一个简单的例子。
以一个3节点系统为例。第1个节点和第3个节点之间有个变电站,每个节点之间设有开关线路。由式(12)得,z21=z23=0,那么y12=z12,y23=z32。由式(15)可知z12+z32=1,因此y12或y23为0,导致放射式网络重构中,2条馈线之间不存在路径。下面的参数普遍延伸到本文后面的模型中。
要求1:任何可行的z必须是0和1,并且,对于每个变电站,描述了一个边缘的、未加权的,有一个根节点的有向树图。
证明:假设y是固定的,令Wy={(i,j∈Ws∶yij=1}∪WWs,换句话说就是开关闭合的线路和没有开关的线路的集合。考虑以变电站节点为起点通过Wy一条路径,记为节点0。对于任何(0,i)∈Wy,z0i=1由式(13)~式(15),对于任何j∈B{0},zij=1。通过沿着路径归纳可以知道,由变电站节点起始的路径的任何z,必须满足:流进时z为0,流出时z为1。因此,2条起始于同一个变电站节点的路径不能满足(因为起始于同一个变电站节点,会形成一个环)。如果形成了一个不包含变电站节点的环,那么这个环中的节点没有流入任何潮流,式(5)和式(6)不能被满足。由此得出结论:z必须是描述变电站节点的树状图。要满足这一点,Wy自身必须由树构成,这样才能满足所有可行解的结果是放射式重构。
注意到上述公式中的连续变量比必要的多:由等式约束式(13)和式(14)可知,每条线路都需要的变量只有z。然而,由于限制因素是离散的、不连续的变量的数目,为了便于阐述,选择了上述稍微不太有效的表述。此外,期望模型的灵活性是内在的,也就是说,一条潮流只能单向流动的线路可以通过明确设置zij=0或zji=1而被模型容纳。需要注意的是,在可行的重构中,连接在一起的每个部分只能有1个变电站节点。
2.2二次约束二次规划
把本文的框架扩展到QCP,通过3种方式增强模型的能力。首先,线路潮流约束可以描述为p2ij+ q2ij≤S2ij,此处S表示线路容量,这是新的约束;其次,认识到式(5)和式(6)要求流入一个节点的潮流大于负荷加上流出的潮流,如果用式(17)和式(18)替代式(5)和式(6),那么损耗就近似考虑在潮流平衡中,即
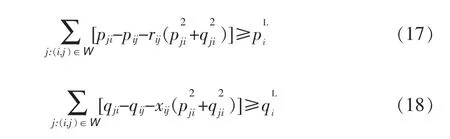
剩下的QP约束不变。由于潮流平衡考虑了损耗,则变电站节点潮流总和为

式(19)可以代替式(4),等效作为减小损耗的目标函数。第三,文献[2]中的负荷平衡表达式通过增加约束被接纳,而且最小化了目标t,即

实际上,QCP问题通常用SOCP算法解决。
2.3SOCP规划
本文推导出二阶锥规划的近似Distflow方程,和式(3)相比,仅仅缺少最后一项,从而允许电压变化远离标幺值。这样的修改是合理的,因为电阻和电抗标幺值的平方使得此项比其他项小得多。此近似表达式由以下约束替代式(5)和式(6)获得。约束的集合用Φ表示,即

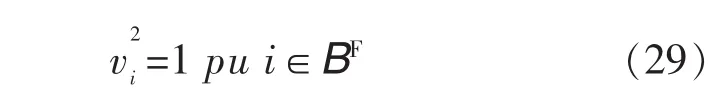
再次在式(23)、式(24)、式(27)、式(28)中使用只有在zji=1才“有效”的分离性约束。具体而言,这些约束的组合等价于当zji=1时式(3)去掉最后一项,当zji=0时等价于强制没有约束(假设M足够大)。式(23),式(24)~式(26)的组合当zji=1时,重现式(1)、式(2),当zji=0时,再次有效地非强制。
式(25)和式(26)是双曲函数约束,属于SOCP问题最广泛的一类约束。就QCP和LP问题而言,可以写成SOCP形式的任何约束都是凸的,适合SOCP算法的。这一点有上述集合验证,因为上述约束都是有LP,QP和SOCP的约束组成。引入额外变量p~i和q~i的目的是把约束化为SOCP的形式,以便可以被商业软件识别。对于固定的网络,这些约束和第2.2部分的二次约束构成了新的放射性网络近似潮流方程。
SOCP是凸的QCP问题的多项式时间内的概括,可以用内点算法高效地解决。虽然混合整数SOCP没有达到混合整数LP和混合整数QP的成熟程度,但是可以通过商业解算器用分支定界法解决。此外,割平面法和改进的连续松弛法是研究的热点,因此,在不远的将来会有大幅改善。
3 算例分析
用本文中的各种模型对69节点系统进行重构。69节点配电网系统,有74条支路,5个联络开关,如图1所示[8]。对于所有的节点i增加约束
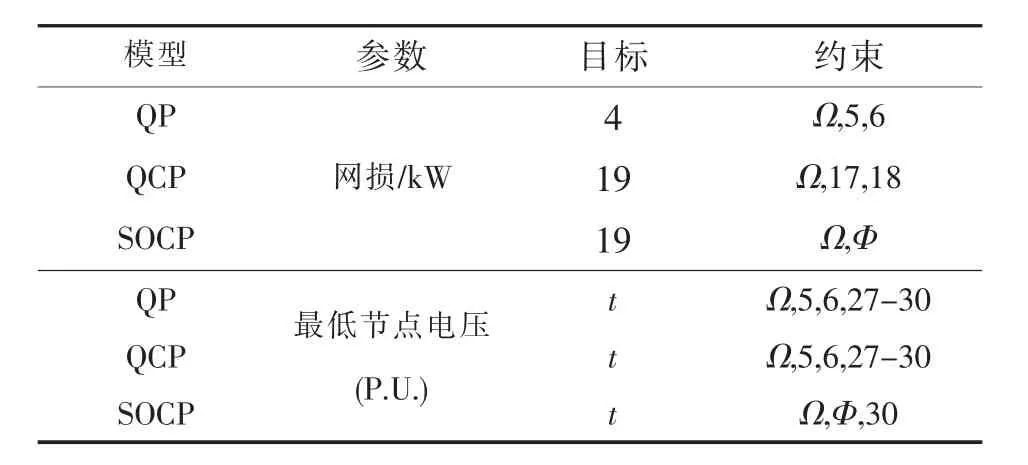
表1 算例中的目标和约束Tab.1 Objectives and constraints of the example

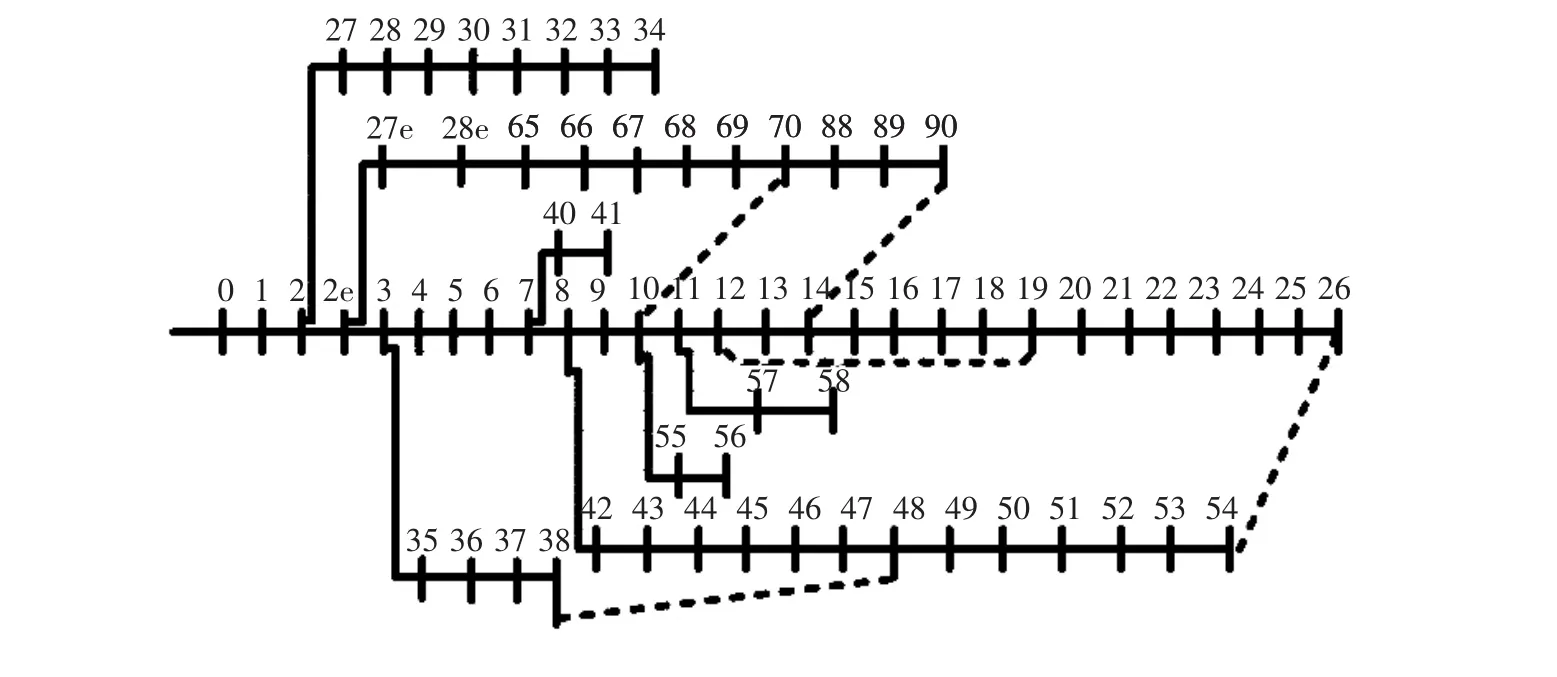
图1 69节点配电网系统Fig.1 Schematic diagram of 69-bus distribution system
这样用简化的DistFlow方程处理最低节点电压实际上是一个线性规划问题。
表1中总结了算例中的目标函数和约束。
由此产生的混合整数规划可以用AMPL建模语言和CPLEX解算器在目前水平计算机上解决。可以说CPLEX能够方便地解决本文的所有问题,而不用调用其他程序。
表2给出了本文每个模型的计算结果和计算速度。当然,所有的网络结构都是放射性的。从表中可以看出,通过配电网重构,不仅网损显著降低,而且节点电压质量得到很好改善。同时可以看出,QCP和SOCP模型比QP模型更精确,但是使用目前可用的算法要花费相当长的时间。增加电阻和电抗会阻碍所有模型的性能,因为QP不考虑约束的损耗,期望QCP和SOCP模型在这种情形下保持比QP更好的精度。

表2 配电网重构前后结果Tab.2 Results before and after reconfiguration
4 结语
本文介绍了3种配电网重构的混合整数规划凸模型,并且这些模型都可以使用强大的凸优化算法。算例表明二次规划模型是有效的,并且实用性很强。二阶锥规划在产生可靠解决方案时更有效,但是计算代价稍高。待混合整数二阶锥规划算法得到实质性的改进后,SOCP和QCP模型会成为更具扩展性的选择。各个模型另一个亮点是利用已有商业软件的便利性,并且其可扩展性可以通过对最优标准进行松弛达到。未来进一步的研究工作包括更好地了解对最优性要求进行松弛的方法,以及如何利用正在改进的混合整数二阶锥规划算法。
[1]Baran M E,Wu F F.Network reconfiguration in distribution systems for loss reduction and load balancing[J].IEEE Trans.Power Del.,1989,4(2)∶1401-1407.
[2]Chiang H D,Jean J R.Optimal network reconfigurations in distribution systems—I∶A new formulation and a solution methodology[J].IEEE Trans.Power Del.,1990,5(4)∶1902-1909.
[3]Nara K,Shiose A,Kitagawa M,et al.Implementation of genetic algorithm for distribution systems loss minimum reconfiguration[J].IEEE Trans.Power Syst.,1992,7(3)∶1044-1051.
[4]Braz H D,Souza B A.Distribution network reconfiguration using genetic algorithms with sequential encoding∶Subtractive and additive approaches[J].IEEE Trans.Power Syst.,2011,26(2)∶582-593.
[5]Chang H C,Kuo C C.Network reconfiguration in distributionsystemsusingsimulatedannealing[J].ElectricPowerSyst.Res.,1994,29(3)∶227-238.
[6]赵晶晶,李新,彭怡,等.基于粒子群优化算法的配电网重构和分布式电源注入功率综合优化算法[J].电网技术,2009,33(17)∶162-166.
Zhao Jingjing,Li Xin,Peng Yi,et al.A comprehensive optimization algorithm for injection power of distributed generation and distribution network reconfiguration based on particle swarm optimization[J].Power System Technology,2009,33(17)∶162-166(in Chinese).
[7]Khodr H M,Martinez-Crespo J,Matos M A,et al.Distribution systems reconfiguration based on OPF using Benders decomposition[J].IEEE Trans.Power Del.,2009,24 (4)∶2166-2176.
[8]蒙文川,邱家驹.基于免疫算法的配电网重构[J].中国电机工程学报,2006,26(17)∶25-29.Meng Wenchuan,Qiu Jiaju.An artificial immune algorithm to distribution network reconfiguration[J].Proceedings of the CSEE,2006,26(17)∶25-29(in Chinese).
[9]许立雄,吕林,刘俊勇.基于改进粒子群优化算法的配电网络重构[J].电力系统自动化,2006,30(7)∶27-30,79.Xu Lixiong,Lü Lin,Liu Junyong.Modified partiele swarm optimization of reconfiguration of distribution network[J].Automation of Electric Power Systems,2006,30(7)∶27-30,79(in Chinese).
[10]刘柏私,谢开贵,周家启.配电网重构的动态规划算法[J].中国电机工程学报,2005,25(9)∶29-34.Liu Bosi,Xie Kaigui,Zhou Jiaqi.Electrical distribution networks reconfiguration using dynamic programming[J].Proceedings of the CSEE,2005,25(9)∶29-34(in Chinese).
[11]Gomes F V,Carneiro S,Pereira J L,et al.A new distribution system reconfiguration approach using optimum power flowandsensitivityanalysisforlossreduction[J].IEEETrans.Power Syst.,2006,21(4)∶1616-1623.
[12]葛少云,刘自发,余贻鑫.基于改进禁忌搜索的配电网重构[J].电网技术,2004,28(23)∶22-26.Ge Shaoyun,Liu Zifa,Yu Yixin.An improved TABU search for reconfiguration of distribution systems[J].Power System Technology,2004,28(23)∶22-26(in Chinese).
[13]毕鹏翔,刘健,张文元.配电网络重构的改进支路交换法[J].中国电机工程学报,2001,21(8)∶98-103. Bi Pengxiang,LiuJian,Zhang Wenyuan.A refined branchexchange algorithm for distribution networks reconfiguration[J].Proceedings of the CSEE,2001,21(8)∶98-103(in Chinese).
[14]兰华,李政阳,王韵然.风光互补发电系统对配电网可靠性的影响[J].电源学报,2012,10(6)∶92-96,106.
Lan Hua,Li Zhengyang,Wang Yunran.Research on the influence of wind-solar hybrid power supply system to the reliability of distribution network[J].Journal of Power Supply,2012,10(6)∶92-96,106(in Chinese).
RONG Desheng,HU Jushuang
(Faculty of Electrical and Control Engineering,Liaoning Technical University,Huludao 125105,China)
Convex Model of Distribution System Reconfiguration
Three models of new mixed-integer quadratic,quadratically constrained and second-order cone programming of distribution system reconfiguration are derived,and the AC problem about convex,continuous relaxations is proposed.Each model optimality can be solved reliably and efficiently by standard commercial software.In the course of deriving for each model,the original quadratically constrained and second-order cone approximations model are obtained,to power flow in radial networks.
distribution system reconfiguration;load balancing;mixed-integer quadratic programming;second-order cone programming.

荣德生
荣德生(1975-),男,博士,副教授,研究方向:节能型电力电子技术及应用,E-mail:345178299@qq.com。
2015-09-14
胡举爽(1990-),男,通信作者,硕士研究生,研究方向:配电网络重构、规划与可靠性,E-mail:1403436227@qq.com。

