基于粒子群优化算法和变步长扰动观察法的局部阴影情况下MPPT控制

马　昊，张庆超

（天津大学电气与自动化工程学院，天津300072）

基于粒子群优化算法和变步长扰动观察法的局部阴影情况下MPPT控制

马昊，张庆超

（天津大学电气与自动化工程学院，天津300072）

针对光伏阵列的输出特性在局部阴影情况下具有高度非线性、时变性以及多个局部功率极值点等特点，并导致传统MPPT（maximum power point tracking）算法失效的问题，提出一种基于粒子群优化算法和变步长扰动观察法的改进MPPT算法。其中粒子群优化算法用于系统启动和光照情况发生突变后迅速定位近似最大功率点，变步长扰动观察法则根据实际状况使光伏阵列精确稳定在最大功率点，以克服使用数学模型与实际输出特性偏差或微小扰动所导致的功率损失。通过建立Matlab/Simulink模型进行仿真实验，实验结果表明所提算法使光伏阵列在不同阴影情况下以及发生光照强度突变时都具有迅速精确的跟踪能力。

局部阴影；MPPT；粒子群算法；变步长扰动观察法

引言

由于太阳能具有取之不尽、用之不竭、无污染、无噪音等优点，光伏发电在新能源应用领域受到越来越广泛的重视并取得快速进步，但发展中也存在许多问题亟需解决，其中太阳能转换效率不高是主要问题［1］。工程上通常采用最大功率点跟踪MPPT （maximum power poiot tracking）算法使光伏阵列输出功率始终维持在最大功率点。在局部阴影等复杂光照条件下，光伏阵列P（UL）特性存在多个功率极值点，导致传统的扰动观察法、电导增量法等无法跟踪全局功率最大值［2］。常见的发生局部遮挡时MPPT方法如下：复合MPPT算法是先把光伏阵列的工作点设在最大功率点的附近范围，再利用扰动观察发或者增量电导法等常规算法进行MPP的定位。因此在搜索局部最优时，在极值点处仍会有振荡，造成功率损失；Fibonacci搜索法基于Fibonacci序列，该算法搜索精度和适应环境突变能力较强，但是收敛速度较慢，实用性不强；短路电流脉冲法是利用光伏阵列的最佳输出电流与短路电流存在的比例关系，周期性引入短路电流脉冲获得光伏阵列输出特性和短路电流来计算最佳输出电流，但引入脉冲对系统的控制性能造成影响，在此期间光伏阵列无法输出功率，因此造成能量的损失。

PSO是一种新型优化算法，在多峰函数优化和多变量系统寻优方面具有良好的性能，并且收敛快、精度高、不易陷入局部最优点，已经有效地应用到解决实际问题当中［3］。但将其用在基于理论光伏电池数学模型的局部阴影条件下MPPT控制时，由于该模型与实际光伏特性有出入，导致输出功率与真正功率最大值有一定差距，且当系统有微小扰动时，此方法不能根据具体情况迅速跟踪最大功率点［4］；再由于算法初始化的随机性，对收敛速度有一定影响，可能影响MPPT控制效果。变步长扰动观察法和常规扰动观察法一样，在复杂光照条件下容易陷入局部最优点，但在最大功率点附近的跟踪精度、发生微小扰动后响应速度以及稳态功率损失等方面体现出更好的适用性［5］。

因此，本文结合光伏阵列在局部阴影条件下的工作特征，提出基于PSO和变步长扰动观察法的复合MPPT控制方法，利用PSO快速定位近似最大功率点，然后通过变步长扰动观察法寻找准确值。搭建Matlab/Simulink仿真模型进行实验，证明了该方法在局部阴影光照条件下以及阴影情况发生突变时都能够快速准确地定位、跟踪最大功率点，始终保持良好的控制性能。

1　局部阴影条件下光伏阵列的等效模型

1.1光伏电池数学模型

利用PN结接受太阳光照产生光生伏特效应制成的光伏电池可以视作一个恒定电流源和一支正向二极管的并联回路，其等效电路如图1所示。其中Iph为光生电流，其值与光伏电池的受光面积、入射光的光照强度以及电池本体温度成正比；Id为光伏电池内部暗电流；Ish为通过旁路电阻Rsh的电流；UL、IL为负载RL上的电压和电流；Rs为串联电阻。由等效电路可得光伏电池的ILUL特性方程为

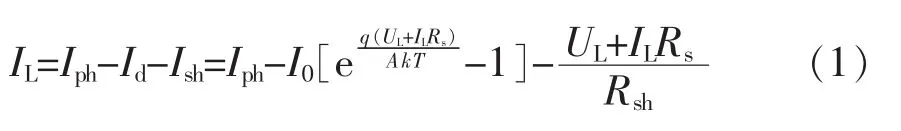
式中：I0为太阳能板的逆向饱和电流；q为电子电荷量；k为波尔兹曼常数；A为PN结曲线常数；T为温度。理想情况下Rsh→∞，式（1）中最后一项即可忽略。

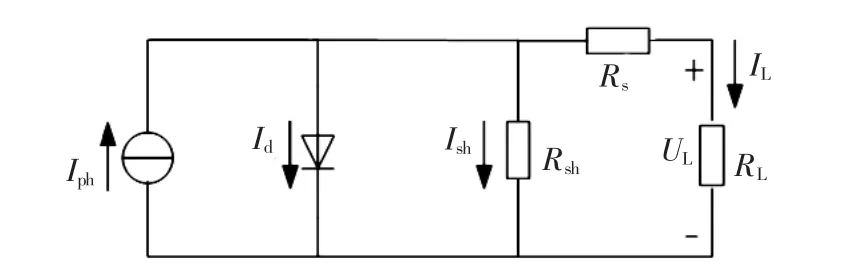
图1　光伏电池等效电路Fig.1　Equivalent circuit of PV cell

实际应用中通过串、并联电池单元来构成光伏阵列以获得期望的输出电压、电流和功率。在均匀光照条件下光伏阵列的ILUL特性方程［6］为

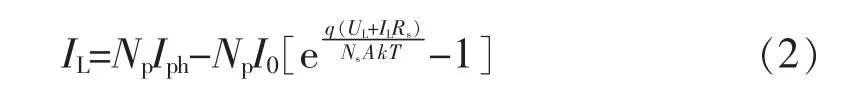
式中，Ns、Np分别为串、并联电池单元的个数。此时光伏阵列的输出IL-UL、P-UL特性曲线如图2、图3所示。

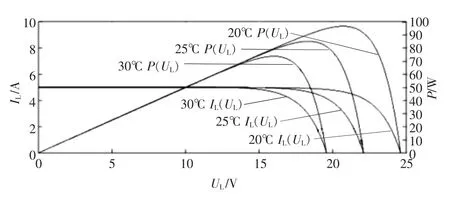
图3　光伏电池输出特性随温度的变化曲线（s=1 000 W/m2）Fig.3　Relationship of output characteristics between PV cell and temperture（s=1 000 W/m2）

由图可见，在均匀光照条件下PUL曲线具有单一峰值特性，并且光伏电池输出功率随着温度升高和光照强度降低而减小，从而导致发电效率下降。

1.2局部阴影条件下的光伏阵列模型

一旦光伏阵列部分组件被遮挡，导致光照不均匀，则被遮挡的组件变成负载，可能产生热斑效应造成永久性损坏［7］。工程中通过并联旁路二极管以避免热斑效应，提高光伏阵列在局部阴影情况下的输出功率。当光伏阵列处于均匀光照情况下，各电池单元都正常工作，旁路二极管处于反向截止状态；当有电池单元被遮蔽时，其光生电流减小，电压变为负压，此时旁路二极管导通将其短路，防止被反向雪崩电流击穿，提高输出功率。并列旁路二极管的光伏阵列结构如图4所示。

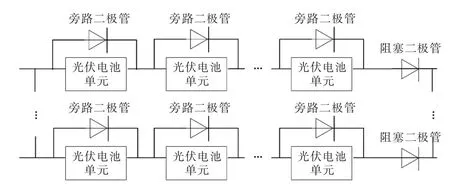
图4　并联旁路二极管的光伏阵列Fig.4　PV array with bypass diode

此时式（2）不再适用，光伏阵列等效模型需重新建立。本文引入光线遮挡率用来表示对光线的遮挡程度，用E表示为

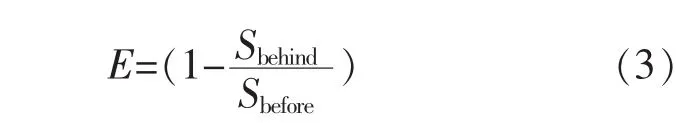
式中：Sbehind为光伏电池单元被阴影遮挡后实际的光照强度；Sbefore为被遮挡前的光照强度。为便于比较，本文中Sbefore均为参考值l kW/m2。

光生电流变为

式中，Iph0为光伏电池在参考光照强度和参考温度下的光生电流。

2个光伏电池单元串联的单串阵列结构如图5所示，图中a单元阴影遮挡，因此Ipha＜Iphb，Ia＜Ib，具体工作模式有如下2种情况：

（1）当RL较大，负载电流IL≤Ia时，电池单元a、b均能正常工作，串联阵列的输出电流由a、b共同提供，输出电压、功率为两者输出电压、功率之和；

（2）当RL较小，负载电流IL＞Ia时，此时电池单元a不能输出相应的电流，被旁路二极管Da短路，于是串联阵列的输出电流由电池单元b提供，输出功率也只由单元b提供。

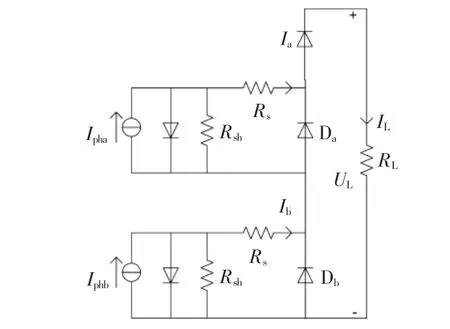
图5　2个光伏单元串联等效电路Fig.5　Equivalent circuit of two series-connected photovoltaic cells

对应于这种情况下的数学模型可表示为

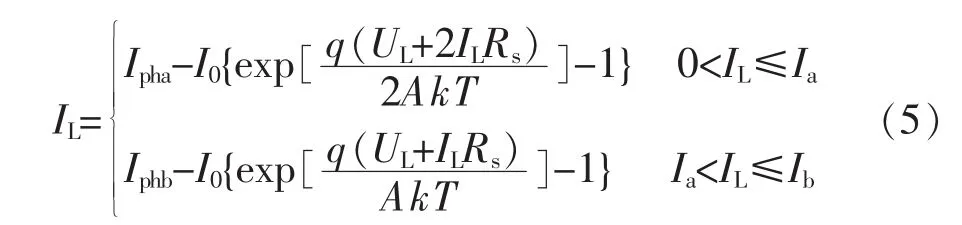
由式（5）建立的光伏电池等效模型的输出特性如图6所示。

图6　局部阴影条件下的输出特性曲线Fig.6　Output characteristics curves of two series-connected PV cells under partial shading

推广到Ns个遮挡面积逐渐减小的电池单元串联构成的光伏阵列，各单元输出电流分别为Ia、Ib、Ic…INs，且Ipha＜Iphb＜Iphc＜…＜IphNs，则其输出特性为

式中，Ix、Ux为单串阵列的输出电流、电压。

2　基于粒子群算法和变步长扰动观察法的MPPT控制

2.1粒子群算法

PSO算法从鸟类捕食的模型中得到启示并用于优化问题的求解。在PSO算法中，每个粒子都有一个由被优化的目标函数f（x）决定的适应度值，优化问题的解为搜索空间中具有最优适应度值的某个粒子。种群内的所有粒子通过不断搜索最终收敛到该粒子周围，粒子的搜索过程通过位置和速度来描述。在MPPT控制中定义光伏阵列输出功率为目标函数，以光伏电池输出电压值来表示粒子的位置，粒子的速度是电压的更新步长，最大功率点所对应的电压为全局最优解。每个粒子的飞行速度和位置更新方程为［3］

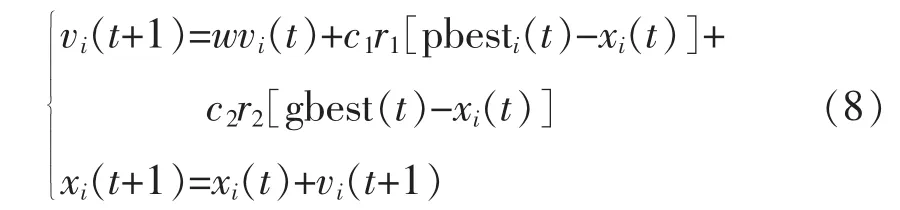
式中：i为第i个粒子；v（t）为粒子t时刻的速度；x（t）为粒子t时刻的位置，搜索位置范围为［xmin，xmax］；pbest（t）为个体最优位置，表示个体所经历的位置中对应的适用度值最好的位置；gbest（t）为全局最优位置，表示当前所有的粒子中适应度值最好的位置；c1、c2为学习因子，一般取2；r1、r2为介于（0，1）之间的随机数，用来调节粒子向pbest（t）、gbest（t）的飞行步长；w为惯性因子，表示粒子历史速度对当前速度的影响。则个体最优、全局最优位置分别为

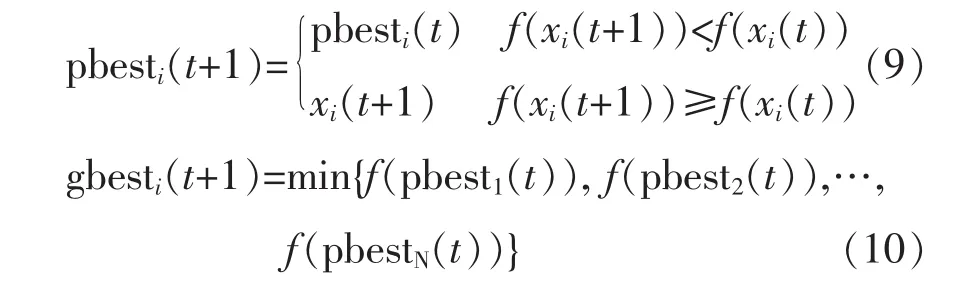
式中，N为粒子的个数。

PSO算法需要设置的参数包括种群粒子数，各个粒子的初始位置以及粒子位置的搜索范围和惯性因子。N的取值大小影响算法的收敛速度以及精度。对于标准PSO算法，种群通过在搜索空间内随机生成N个粒子来初始化，其随机性可能带来收敛速度损失。本文结合局部阴影条件下光伏阵列工作的特殊性对其改进：对于｛m×n｝的光伏阵列，最多对应n+1个极值点［8］，因此令N=n+1，其初始位置分别为U1，U2，…，UN。为了更快速地收敛到全局最优解，首先令 Boost开关管占空比 D=0，得到Uoc_series，然后按式（11）设置初始电压，N取5。粒子位置搜索范围为［0，Uoc_series］。

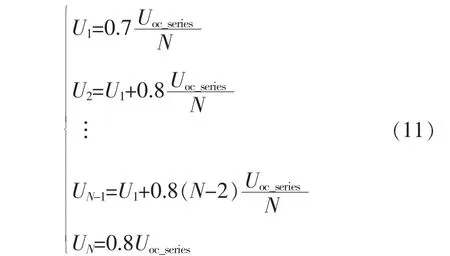
在算法开始阶段，w取较大值可使算法不易陷入局部最优；到算法的后期，w取较小值可使收敛速度加快，使收敛更平稳，不至于出现震荡现象。本文选择对w进行凹函数衰减处理［4］，初始值为0.8。

当达到最大迭代次数时停止迭代，此时所有粒子中对应功率最大的判定为最大功率Pm，其位置即为Um。而当阴影情况或太阳光辐照度发生突变时，光伏阵列输出特性曲线也随之变化，为了提高太阳能利用率需要重新启动粒子群算法求解此时最大功率点。因此系统需要实时检测功率变化量ΔP，即

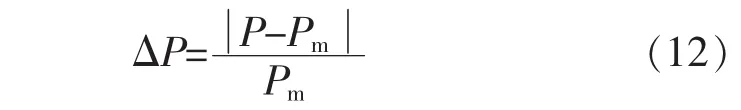
式中：P实时检测到的功率；Pm为之前判定的功率最大值。当ΔP＞0.1时重启PSO算法。

2.2变步长扰动观察法

对于定步长扰动观察法，快速性和精确性存在不可调和的矛盾。扰动步长取较小值时，能够稳态在最大功率点，但是跟踪速度慢、效率低；而取较大值时会缩短跟踪的时间，但会造成稳态时在最大功率点附近的震荡幅度增大，造成功率损失。因此本文采用步长逐次逼近的方法来搜索最大功率点，具体扰动观察过程为：在PSO得到初始工作点的基础上，以较小步长ΔUconst进行扰动，如果在第i+1次扰动之前，始终有Pn+1＞Pn（n＜i），说明当前工作点在最大功率点的左侧，则继续以该步长搜索；当出现Pi+1＜Pi时，说明当前工作点变化到最大功率点的右侧，由此推断出最大功率点的范围应在当前工作点的2ΔUconst范围内。接着以ΔUconst/2为步长进行反方向扰动，直到出现功率方向的下一次改变，此时最大功率点的范围在ΔUconst范围以内，即跟踪精度提高1倍。重复上述过程，每当发生功率方向改变则步长减半，并且改变扰动方向继续搜索，直到最大功率点落在当前工作点的给定精度范围内时，判定为搜索到了最大功率点。

变步长扰动观察法的步长计算公式为

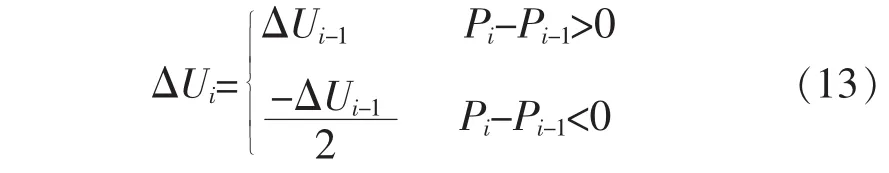
显然，逐步逼近法的精度在扰动搜索过程中以指数形式提高，较好地解决了定步长扰动法跟踪速度和精度间的矛盾，使系统尽快稳定在最大功率点。与此同时，当光照强度缓慢持续变化，ΔP较小，不满足PSO算法突变重启条件，但光伏阵列的工作效率也会降低，此时依据检测到的前后两次功率差的大小判定是否启动逐次逼近法进行最大功率跟踪，及时调整系统输出功率，使太阳能利用率最大化。

2.3控制策略

本文提出的复合MPPT控制算法由2部分组成，第1部分是粒子群寻优过程，第2部分是变步长扰动观察法跟踪过程。控制系统流程如图7所示。各部分的具体步骤如下。

粒子群寻优步骤：①利用式（11）求得各个粒子的初始电压；②检测各个电压对应输出功率，即为粒子的初始pbest，所有粒子对应的最大功率即为初始gbest；③按式（8）更新各个粒子对应电压，将此时的输出功率与该粒子所经历的最大输出功率进行比较，如果当前电压对应的功率较大，则更新pbest；④将所有粒子对应的功率与当前gbest比较，若存在新粒子的输出功率大于gbest，则更新gbest；⑤重复步骤③和④，当满足最大迭代次数时输出PPSO以及对应的UPSO。

变步长扰动算法步骤：①将粒子群寻优得到的电压UPSO作为初始电压；②以ΔUconst为步长进行扰动，检测功率变化ΔP的大小、方向，判断是否需要调整步长；③利用新得到的步长重复上述扰动过程，直到扰动步长减小到某一特定值ε1时，判定系统已稳定在最大功率点；而当ΔP＞0.1时判断为外界环境突变，此时重启PSO算法寻优过程。

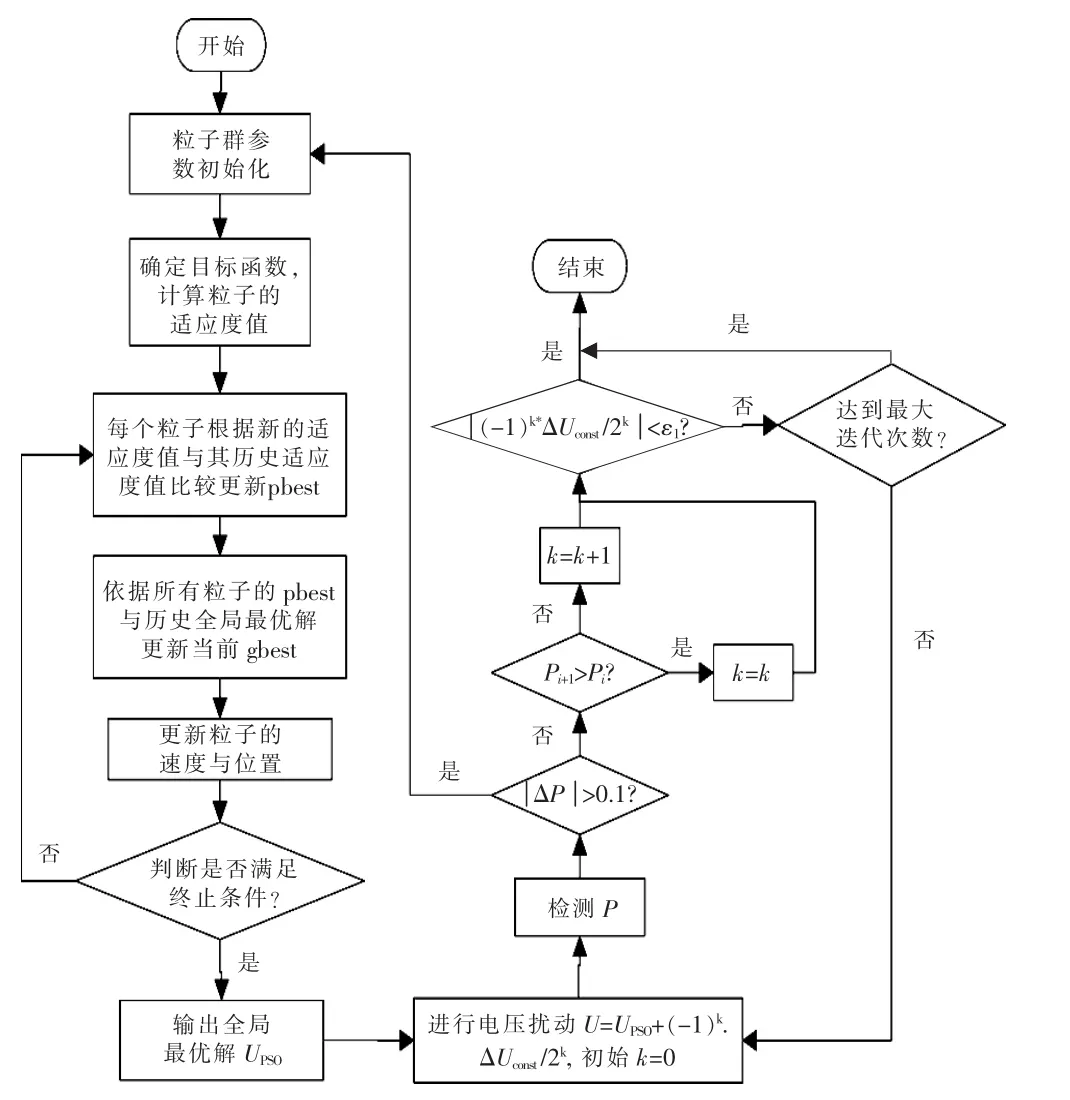
图7　基于复合算法的MPPT控制流程Fig.7　Flow chart of MPPT based on PSO and the improved P&O

3　仿真实验

利用Matlab/Simulink建立4个光伏电池单元组成的串联阵列模型，其参考数据采用BP585U太阳能电池组件的标称参数：在参考温度25℃，参考光照1 000 W/m2的情况下，光伏电池单元Pm=85 W，Uoc=22.1 V，Isc=5 A，Um=18 V，Im=4.72 A［7］。在基于本文提出的复合算法的MPPT控制系统基础上，分别进行局部遮挡情况下MPPT寻优以及光照强度突变后寻优试验，以及系统达到稳态光照强度发生小幅扰动后功率跟踪试验来测验算法性能。在第1个实验中，阴影情况1对应光线遮挡率E1=［0.0，0.0，0.2，0.4］，阴影情况2对应E2=［0.2，0.2，0.6，0.6］。首先在阴影情况1观察算法的收敛速度和精度，检测算法的静态性能；而当这种情况下系统达到稳态，光伏阵列输出功率维持在最大功率点后阴影情况发生突变，观察系统重新达到稳态的时间和振荡过程的强度以检测算法的动态性能。总仿真时长为0.2 s，在t=0.1 s时由E1突变为E2，对应的光伏特性曲线如图8所示；在t=0.15 s时发生辐射度小幅扰动，进行稳态扰动实验。

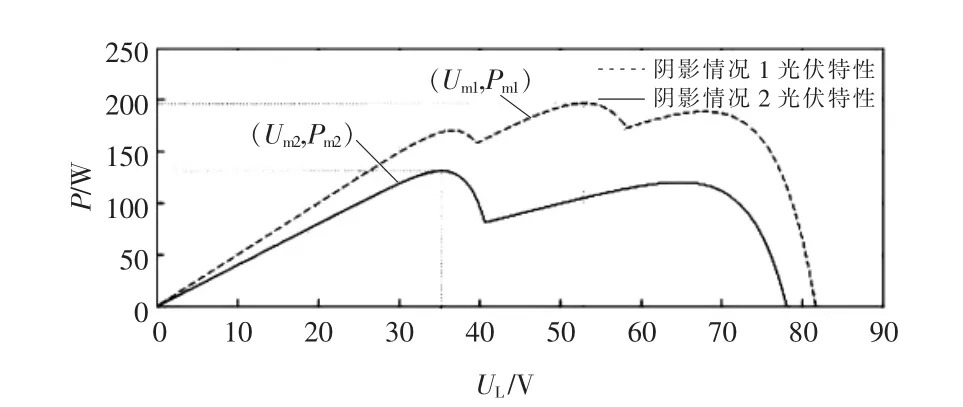
图8　2种阴影情况下的光伏特性曲线Fig.8　Output characteristics of two partial shading modes

在2种阴影情况下的PSO寻优过程初始电压设置如表1所示，其迭代搜索过程以及采用遗传算法进行对比实验的结果如图9所示。遗传算法采用二进制编码，种群个体数与PSO算法相同，变异率取0.06，交叉率取0.6。每一代进化过程中种群中适应度值最优的个体不参加交叉变异操作，以保留优良特性，图9（b）描述的是遗传算法获得的最有适应度值的变化过程。

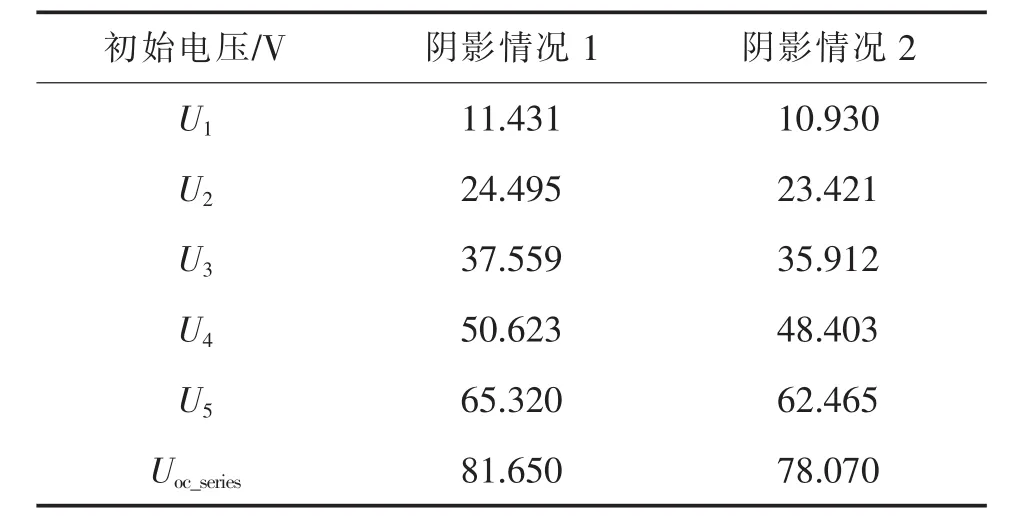
表1　2种阴影情况下各粒子的初始位置Tab.1　Initial position of agents in two partial shoding modes V

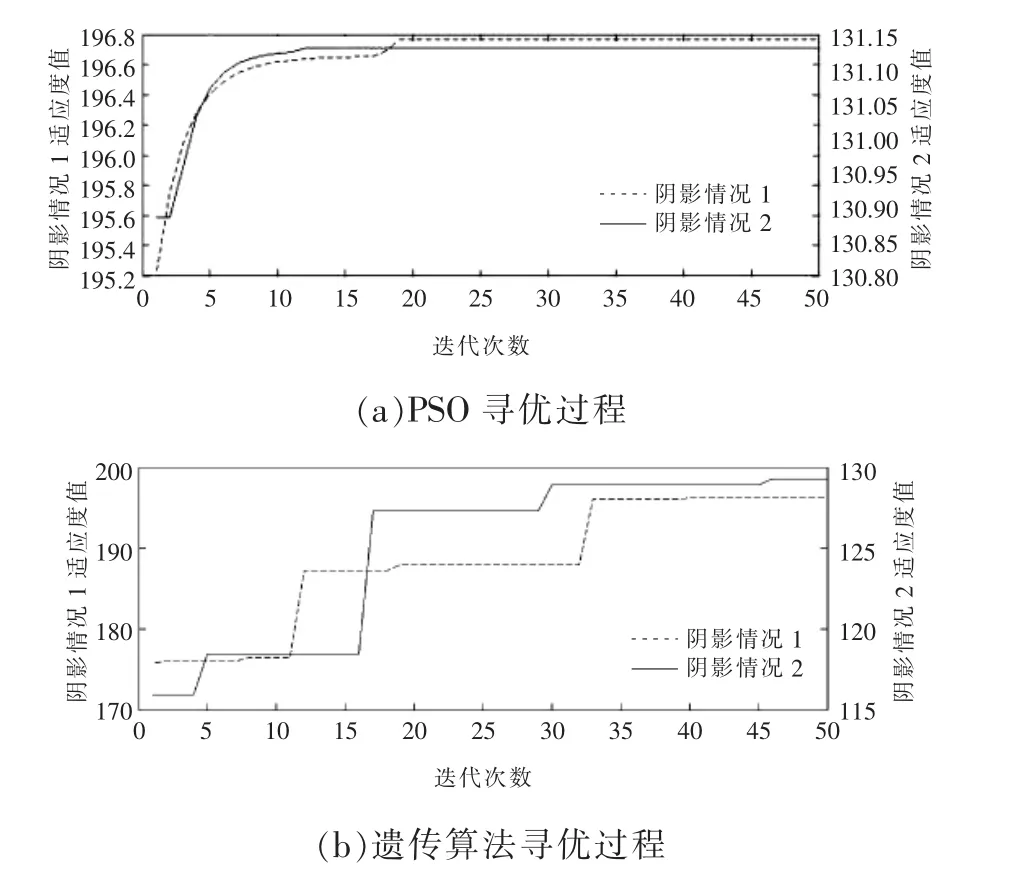
图9　PSO算法与遗传算法寻优对比实验Fig.9　Optimization experiment between PSO and GA

由图可见，PSO算法利用式（11）的初始化机制后能够在不同阴影条件下，经过较少的迭代次数即收敛到全局最优点：E1下经过19次迭代收敛到全局最优解，（Um1，Pm1）=（52.83 V，196.82 W）；E2下经过 12次迭代收敛到全局最优解，（Um2，Pm2）=（35.36 V，131.27 W）。利用pbest、gbest指导进化，这种记忆特性使得迭代过程始终向有利进化的方向进行。与之相比，遗传算法不仅寻优速度不及PSO算法，而且E1下在全局最优点周围搜索缓慢，有限的迭代次数内无法稳定在全局最优点；在阴影情况2下收敛到了非全局最优点，算法失效。

在PSO输出电压参考值的基础上，变步长扰动观察法跟踪过程以及定步长扰动观察法对比实验结果如图10所示。由图10（a）可见，E1下经过0.021 s即可稳定在最大功率点，系统超调和输出功率振荡都比定步长扰动观察法小，而且稳态下输出功率波动小，光伏阵列损失功率少，效率较高；光照强度突变到E2后，又经过0.008 s成功稳定在新的最大功率点。当t=0.15 s发生小幅扰动后，先以较大步长进行跟踪，然后步长迅速减小，经过0.006 s即回复到原始状态，功率振荡时间短，证明了算法具有很好的快速性和精确性。

由图10（b）可见，在E1下功率稳定在167.5 W附近，即第1个局部功率极大点而非全局最大点，并且算法迭代过程中功率振荡严重，超调大，对系统产生巨大冲击；突变后，经过0.014 s才能达到稳定，并且突变前后稳态始终存在振荡，系统功率损失较大。发生小幅扰动后，该算法虽然能够识别扰动，但是经过0.02 s才能稳定，依然存在稳态误差。证明其无法在局部阴影条件下有效地使光伏阵列输出功率跟踪全局最大功率点以及在稳态情况下无法使光伏发电系统效率最大化。

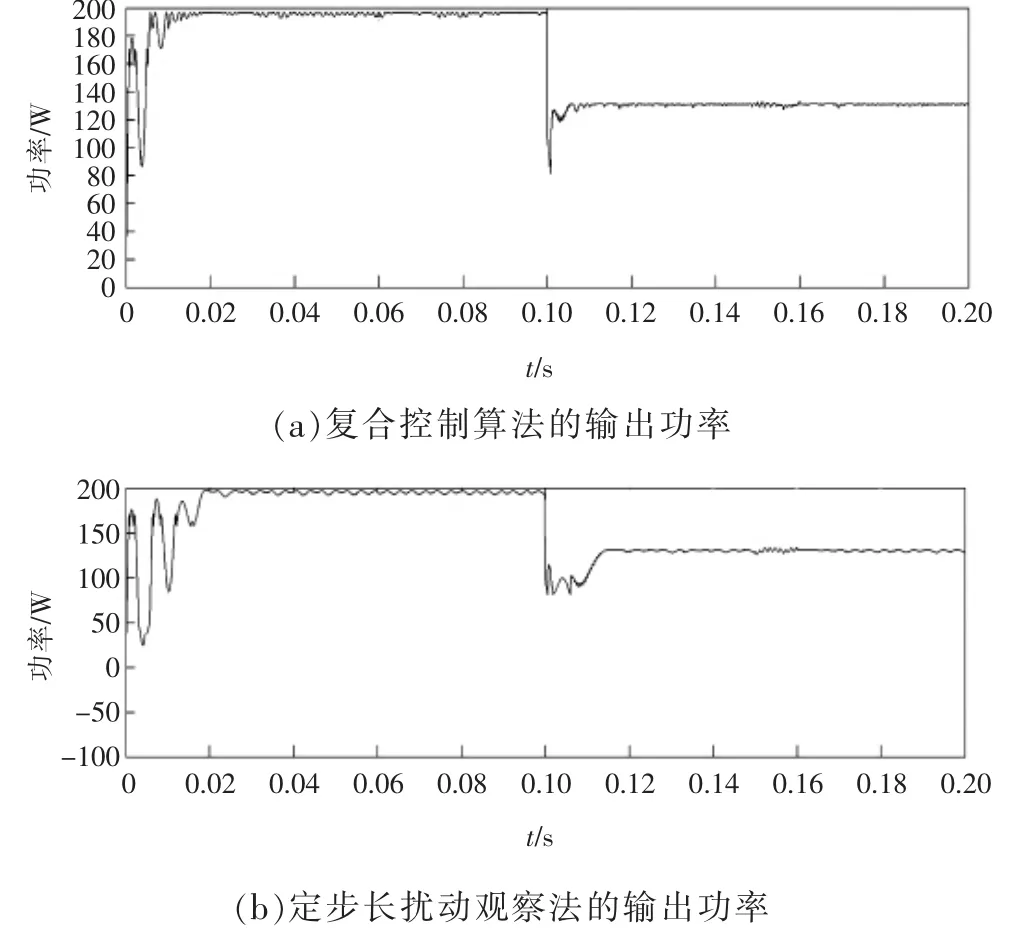
图10　复合控制算法与定步长扰动观察法寻优对比实验Fig.10　Optimization experiment between the recommended MPPT and P&O

4　结语

本文针对局部阴影情况下光伏阵列输出特性具有多个局部极值点的特性，提出一种基于PSO和变步长扰动观察法相结合的复合MPPT算法，并利用Matlab/Simukink搭建模型，与传统的扰动观察法进行对比仿真实验。由仿真结果可看出，采用PSO可快速定位到近似全局最大功率点，响应时间几乎不受搜索范围大小和极值点个数和分布位置的限制，寻优效果优于遗传算法。变步长扰动观察法可以精确稳定在最大功率点，并且在阴影情况突变或者光照强度缓慢变化的情况下都能迅速有效地调整光伏阵列输出功率，具有良好的稳态和动态性能，提高了太阳能利用率；而扰动观察法在局部遮挡条件下无法保证有效性。复合算法实现简单，运行可靠，减少了MPPT控制系统成本，提高光伏发电的经济性，体现出对环境的变化良好的适应能力，具备工程应用的条件。

［1］赵争鸣，刘建政，孙晓瑛，等.太阳能光伏发电及其应用［M］.北京∶科学出版社，2006：1-18.

［2］刘艳莉，周航，程泽.基于粒子群优化的光伏系统MPPT控制方法［J］.计算机工程，2010，36（15）∶265-267.Liu Yanli，Zhou Hang，Cheng Ze.MPPT control method of PV system based on PSO［J］.Computer Engineering，2010，36（15）∶265-267（in Chinese）.

［3］徐刚，瞿金平，杨智韬，等.一种改进的自适应粒子群优化算法［J］.华南理工大学学报（自然科学版），2008，36（9）∶6-10.Xu Gang，Qu Jinping，Yang Zhitao，et al.An improved adaptive particle swarm optimization algorithm［J］.Journal of South China University of Technology（Natural Science Edition），2008，36（9）∶6-10（in Chinese）.

［4］王雨，胡仁杰.基于粒子群优化和爬山法的MPPT算法［J］.太阳能学报，2014，35（1）∶149-153.Wang Yu，Hu Renjie.MPPT algorithm based on particle swam optimization with hill climbing method［J］.Acta En-ergiae Solaris Sinica，2014，35（1）∶149-153（in Chinese）.

［5］张兴.太阳能光伏并网发电及其逆变控制［M］.北京∶机械工业出版社，2011.

［6］钱念书，刘阔，郭建业，等.光伏电池建模及其输出特性研究［J］.电源学报，2012，10（5）∶78-82.Qian Nianshu，Liu Kuo，Guo Jianye，et al.Modeling and output features simulation of photovoltaic cells［J］.Journal of Power Supply，2012，10（5）∶78-82（in Chinese）.

［7］刘晓艳，祁新梅，郑寿森，等.局部阴影条件下光伏阵列的建模与分析［J］.电网技术，2010，11∶192-197.Liu Xiaoyan，Qi Xinmei，Zheng Shousen，et al.Model and analysis of photovoltaic array under partial shading［J］.Power System Technology，2010，11∶192-197（in Chinese）.

［8］朱艳伟，石新春，但扬清，等.粒子群优化算法在光伏阵

MPPT Control Under Partial Shading Condition Based on PSO and Variable Step Size P&O

MA Hao，ZHANG Qingchao
（School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China）

For the photovoltaic array in the case of partial shading has high nonlinearity，time-varying uncertainty and several local peak power characteristics，which resulting in conventional MPPT（maximum power point tracking）algorithms failing to work，an algorithm was proposed based on particle swarm optimization（PSO）and variable step size perturbation and observation（P&O）method.PSO was used to quickly locate approximate maximum power point（MPP）when the MPPT system started or illumination intensity motution occurred，and variable step size P&O method could find precise MPP based on the actual status to overcome power loss caused by the deviation between mathematical model and the actual output or small pertubarions.Matlab/Simulink simulation model was established.The results show that this method has a high precision and rapidity tracking capabilities in the case of partial shading as well as illumination intensity motution.

partial shading；maximum power point tracking（MPPT）；particle swarm optimization；variable step size perturbation and observation method

10.13234/j.issn.2095-2805.2016.3.94

TM 615

A

2015-09-06