一种基于模糊核聚类算法的图像分类方法

王书文，皮炳坤，张弘强，马　聪



一种基于模糊核聚类算法的图像分类方法

王书文，皮炳坤，张弘强，马聪

(西北民族大学电气工程学院，甘肃兰州730030)

聚类分析是数据分析的一个重要方法.通过引用核函数，将核方法应用到模糊C均值(Fuzzy c-Means,FCM)算法中，优化FCM算法的目标函数，使样本点被非线性变换映射到高维特征空间进行聚类,不仅改善了聚类效果，而且增强了算法对噪声的鲁棒性.在真实样本集上进行了仿真实验，分类结果证实了该算法的有效性和普适性，因而是一种较为简单和实用的图像分类方法.

聚类分析；子空间聚类；核函数；核模糊聚类算法

近年来，模糊聚类分析技术是智能信息处理中的一个热门课题,它用一种模糊数学方法来研究聚类问题,是一种无监督的模糊模式识别方法,在模式识别及分类、图形图像处理、以及计算机视觉等领域有着广泛的应用[1-6].

目前普遍应用的聚类分析方法有K-均值法[1]和模糊C-均值法[2]等.在多种模糊聚类分析算法中，由Dunn[3]首先提出后又被Bezdek[4]加以推广的模糊C 均值算法是一种很有效的方法.模糊C-均值聚类算法因其算法简单、收敛速度快等优点受到广泛关注.而Bezdek提出的模糊聚类算法FCM则通过引入像素聚类样本到聚类中心的隶属度来表示像素样本的隶属度，该类隶属度的大小能够客观反映出算法中样本点隶属于某一类的程度[5].虽然FCM算法计算简单，复杂度较低，但在很多情况下该算法对噪声敏感.Girolami[6]和张莉等[7]将核函数引入到聚类分析中，在高维特征空间中进行聚类；曲福恒等[8]利用Zangwill收敛性定理，证明了核模糊C-均值聚类算法(KFCM)的收敛性；范成礼等[9]对模糊核聚类算法进行了直觉化扩展，提出一种基于核化距离的直觉模糊聚类(IFKCM)算法，但其收敛速度较慢，易陷入局部最优解等难题.

用核方法改造传统的学习算法是当今机器学习领域的一个热点.因此，模糊核聚类算法[10]在一定程度上能够克服传统FCM 算法不适合多种数据结构的缺陷，并具有普适性，能够容忍噪声，具有广泛的应用价值.基于以上分析，本文将模糊核聚类算法应用到低维空间中的子空间聚类问题来实现数据的分类.

1　核模糊C均值聚类算法

核模糊C均值聚类(KFCM)算法的基本思想是选取相应的核函数替代FCM算法中的欧氏距离，将低维输入空间的非线性问题转换为高维特征空间的线性问题.而FCM的目标函数为

(1)

(2)

引入核方法，则可将目标函数转化为

(3)

其中Φ为特征映射，根据核方法中的转换技巧，可做如下转换

(4)

在此选取高斯核函数

(5)

根据

(6)

结合K(x，x)= 1,则目标函数可转化为

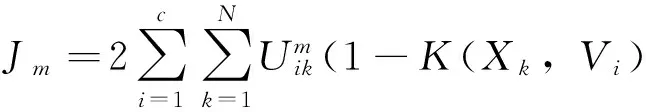
(7)

为了最小化目标函数，结合约束条件，得到聚类中心和隶属度矩阵的更新公式为

(8)

(9)

根据上式不断迭代求出满足条件的隶属度以及聚类中心，从而最小化目标函数.为保证算法收敛，KFCM算法具体步骤为:

1)设定类别的个数C和模糊系数m，初始化隶属度矩阵且满足归一化条件；

2)根据(9)式确定聚类中心Vi；

3)根据(8)式更新隶属度矩阵U；

4)根据矩阵范数比较迭代的隶属度矩阵，若收敛，迭代停止，否则返回步骤2.

2　结果与分析

为了验证该算法的有效性和可行性,本文选取了一组三个低维空间中的子空间聚类问题和两个实际应用中的聚类问题[11]来进行仿真实验.实验在Matlab 7.0软件环境下完成,利用改进的核模糊C均值聚类KFCM算法可实现对数据的分类.

一组低维空间的样本集采用改进的核模糊C均值聚类KFCM算法，将其分为两类的结果如图1所示.其中，图1(a)为两条交点不在原点且互相垂直的直线;图1(b)为两条不相交的二次曲线;图1(c)为两条相交的螺旋线.为了测试FCM聚类算法和改进的模糊核聚类算法的聚类性能，将上述两个聚类算法在真实数据集上进行实验对比分析，其结果见表1.

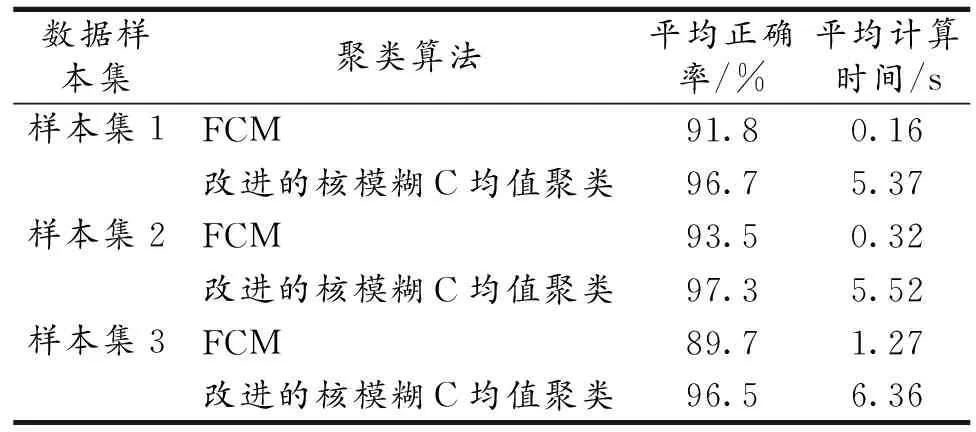
表1　人工数据实验结果比较(20次随机实验)

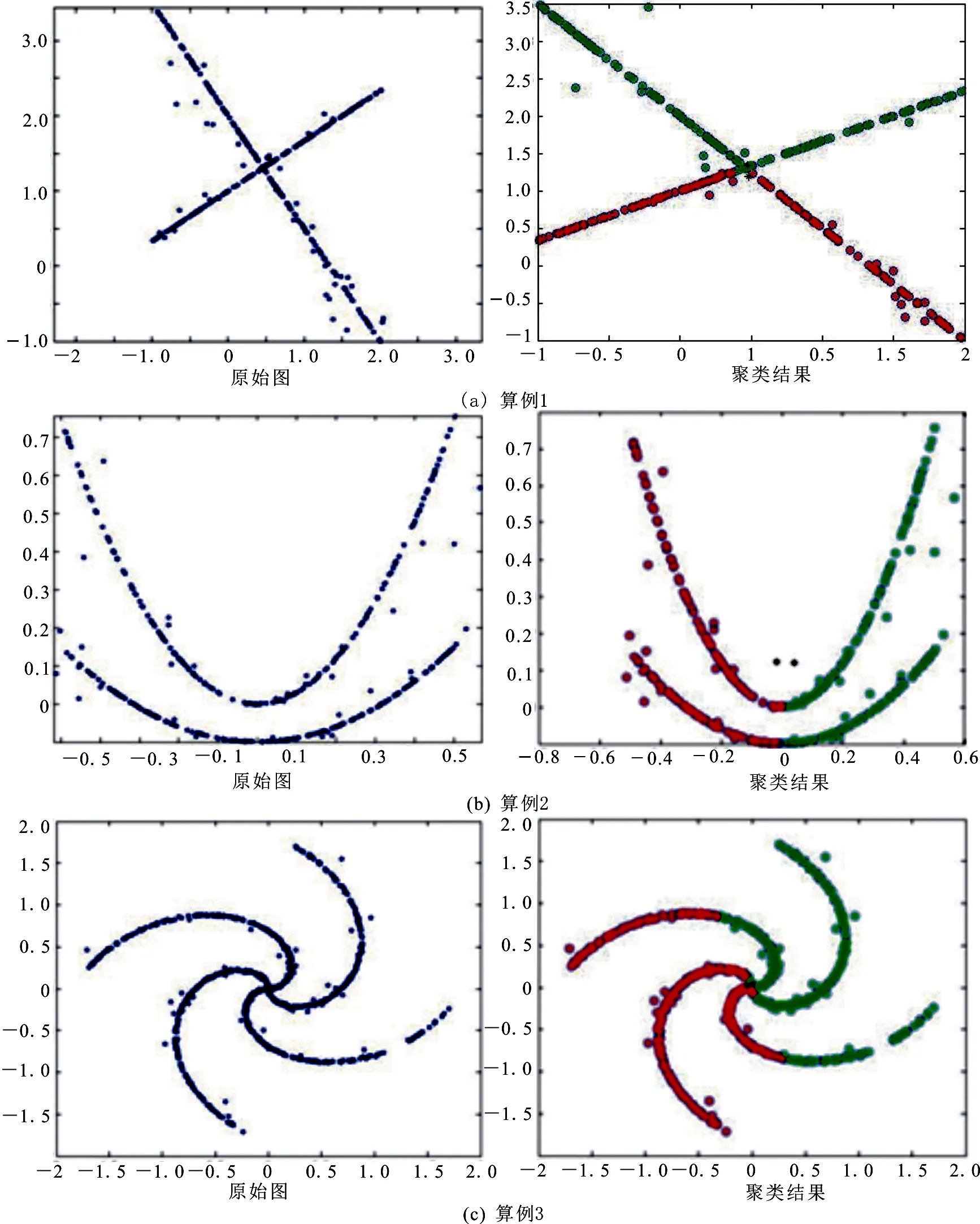
图1　不同算例原始图及聚类结果

由表1可以看出，其分类结果较好.而模糊核聚类算法比FCM算法在各方面均有一定的改善，而提出的改进模糊核聚类算法在正确率上有了提升，与一些FCM等聚类算法相比，明显提高了聚类的稳定性.

在实际应用中，基于特征点轨迹的方法是重要的一类运动分割方法，有文献指出同一运动的特征点轨迹在同一个线性流形上，而图2(a)给出了视频中的一帧，有三个不同运动的特征点轨迹被提取出来保存在了样本文件中，利用改进的核模糊C均值聚类KFCM算法，将这些特征点轨迹分成三类的结果见图2(b)所示.

从图中可以看出,其改进的模糊核聚类算法的分类正确率也达到了94.62%，能有效防止小数据类被误分的情况，进而得出改进的模糊核聚类(KFCM)算法的方法是有效的，能客观反映其实际情况.

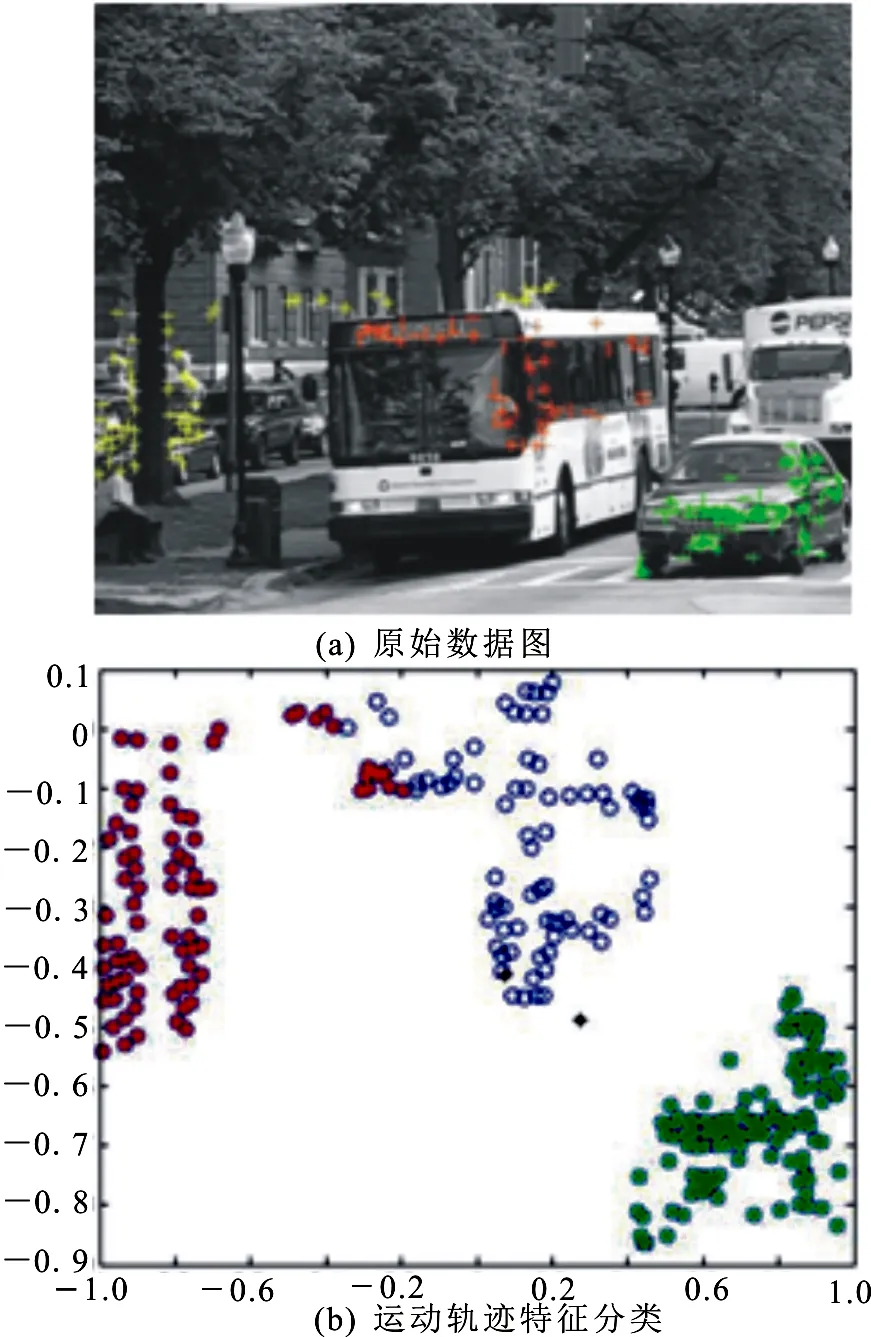
图2　原始数据图及分类结果

3　结束语

本文分析了一种改进的模糊核聚类(KFCM)算法,通过核函数对数据进行隐性的非线性映射，较好地实现了对差别微弱的样本类之间的聚类，使得算法能取得良好的分类结果.该聚类方法在性能上比经典聚类算法有所改进,具有较高的准确度.仿真实验结果证实了算法的可行性和可靠性.而未来发展中，如何把KFCM算法与蚁群算法、粒子群等智能算法相结合是研究的重点，并如何根据实际问题选用合适的核函数及最优参数也是一大重点.今后将采用聚类有效性指标作为适应度函数，利用多目标优化算法进行同时优化，进一步提升聚类方法的稳定性.

[1]JAIN A K.Data clustering:50 years beyond K-means[J].PatternRecognitionLetters,2010,31(8):651.

[2]ZBAY Y,CEYLAN R,KARLIK B.Integration of type-2 fuzzy clustering and wavelet transform in a neural network based ECG classifier[J].ExpertSystemswithApplications,2011,38(1):1004.

[3]DUMN J C.A graph theoretic analysis of pattern classification via tamura’s fuzzy relation[J].IEEETransonFuzzySystem,1974,4(3):310.

[4]BEZDEK J C.PatternRecognitionwithFuzzyObjectiveFunctionAlgorithms[M].New York:New York Plenum Press,1981.

[5]CHUANG K S，TZENG H L，CHEN S，et al.Fuzzy c-means clustering with spatial information for image segmentation[J].JournaloftheComputerizedMedicalImagingSociety,2006,30(1):9.

[6]GIROLAMI M.Mercer kernel based clustering in feature space [J].IEEETransonNeuralNetworks,2002,13(3):780.

[7]张莉，周传达，焦李成.核聚类算法[J].计算机学报，2002，25(6)：587.

[8]曲福恒，胡雅婷，马驷良,等.基于核的模糊C-均值聚类算法的收敛性定理[J].吉林大学学报(理学版)，2011，49(6)：1079.

[9]范成礼,邢清华,付强,等.基于直觉模糊核聚类的弹道中段目标识别方法[J].系统工程与电子技术,2013,35(7):1362.

[10]彭建喜.一种基于C均值的模糊核聚类图像分割算法[J].电视技术，2014,38(9):28.

[11]罗四维.视觉信息认知计算理论[M].北京:科学出版社，2010.

(责任编辑孙对兄)

An image classification method based on fuzzy kernel clustering algorithm

WANG Shu-wen,PI Bing-kun，ZHANG Hong-qiang,MA Cong

(College of Electrical Engineering,Northwest University for Nationalities,Lanzhou 730030,Gansu,China)

The clustering analysis is a crucially important method for data analysis.By referring to kernel function,the kernel method is applied to the fuzzy C-means(fuzzy C-means, FCM) algorithm,optimizing objective function of FCM algorithm,sample points are mapped to high-dimensional feature space by the nonlinear transform cluster.The method can not only improve the clustering effect,but also enhance the algorithm robustness to noise.Simulated experiments are conducted on real sample set,the classification results prove the effectiveness and generalizability of the algorithm,so this algorithm is a relatively simple and practical method.

cluster analysis;subspace clustering;kernel function;nuclear fuzzy clustering algorithm

10.16783/j.cnki.nwnuz.2016.05.010

2016-03-08;修改稿收到日期:2016-07-03

国家自然科学基金资助项目(61261042)；西北民族大学中央高校基本科研业务费专项资金资助研究生项目(YXM2015215)

王书文(1965—)，男，河南扶沟人，教授，硕士研究生导师.主要研究方向为图像处理与密码学.

E-mail:294171424@qq.com

TP 311

A

1001-988Ⅹ(2016)05-0042-04