基于MPCK理论的数学教育专业毕业生综合评价
叶茶花,付柳林
基于MPCK理论的数学教育专业毕业生综合评价
叶茶花,付柳林
(九江学院 理学院,江西 九江 332005)
以数学教育专业学生成绩为研究对象,采用多元统计中的因子分析法,探索学生成绩所蕴含的规律,结合MPCK理论提取4个有实际意义的因子,根据因子得分算出学生综合排名.该综合评价不仅为选拔优秀的数学教师提供依据,而且可以从定量的角度评价课程设置的效果.
MPCK理论;学生成绩;综合评价
MPCK(Mathematics Pedagogical Content Knowledge)是近几年数学教育研究的热点问题[1],由数学学科知识(MK)、一般教学法知识(PK)、有关数学学习的知识(CK)和教育技术知识(TK)融合而成.它是数学教师从事专业教学所应具备的核心知识.每年招收的中小学数学教师基本都来自各大院校数学教育专业的毕业生,因此,从MPCK视角对数学教育专业毕业生进行综合评价显得至关重要.
本文以数学教育专业学生成绩为研究对象,采用多元统计中的因子分析法[2],探索学生成绩所蕴含的规律,结合MPCK理论提取4个有实际意义的因子,根据因子得分算出学生综合排名.
1数据来源及指标选取
本文原始数据来自于某高校数学教育专业毕业生的13门主干课的考试成绩.课程名称及编号见表1.
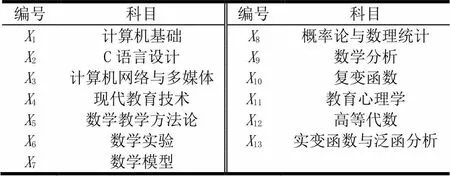
表1 课程科目及编号
2实证研究
因子分析的主要目的在于找出公共因子,希望以最少的公共因子对总变异量作最大的解释[3],因此抽取的因子愈少愈好,但抽取因子的累积解释的变异量愈大愈好.具体过程为[4]:
Step2 建立变量的相关系数矩阵,计算特征值、贡献率和累计贡献率(见表2).

表2 主成份信息
Step3 建立因子载荷阵,对因子载荷阵实行方差最大正交旋转,结果见表3.

表3 旋转后的因子载荷矩阵
Step4 用回归法计算出因子得分信息(见表4).

表4 因子得分矩阵
3结果分析
学生13门课程成绩之间存在着较强的相关性,也就是它们所包含的信息有许多是重复的,因此可以考虑应用因子分析的方法将这13个指标进行有效的压缩.由表2可以看出,有4个因子的特征根大于1,根据需要和结合实际情况,选取前4个因子作为公共因子,分别记为,,,.4个因子的方差累计贡献率为80.887%,可以认为这4个因子反映了原始变量的大部分信息.
由表3可以看出,公共因子在许多变量上有较高的载荷.经方差最大正交旋转后,可以更清楚地确定和解释公共因子的实际意义.如因子在变量,,上有着较高的载荷,它主要反映了学生在师范教育类课程方面的相关信息,可命名为PK因子;因子在变量,,,,上有着较高的载荷,它主要反映了学生在数学专业课程方面的相关情况,可命名为MK因子;因子在变量,,上有着较高的载荷,它主要反映了学生在计算机课程方面的相关信息,可以命名为TK因子;因子在变量,上的载荷较高,它主要反映了学生在数学应用课程方面的相关信息,可以命名为CK因子.根据对相关课程的了解,上述的因子结构确实是合理的.
4因子的综合评价
由表4的因子得分矩阵,可以建立起因子得分函数,即

