两种地图投影之间的转换实现

■许冰 吴扬扬

（沈阳市勘察测绘研究院辽宁沈阳110004）

两种地图投影之间的转换实现

■许冰 吴扬扬

（沈阳市勘察测绘研究院辽宁沈阳110004）

本文主要介绍了横轴墨卡托投影和斜轴墨卡托投影的基本原理，并以具体的地形图为例,利用VB对AutoCAD的二次开发实现了这两种常见地图投影之间的转换。

墨卡托投影 投影转换

0 前言

圆柱投影是以假想一个足够大的椭圆柱面套在地球表面，与地球的某一经线圈或赤道相切，椭圆柱面的中心轴线恰好穿过椭球体中心，然后按照一定的投影公式，将所切子午线（即中央子午线）两侧一定经差范围内的地区投影到圆柱面上后，将圆柱面展为平面即完成圆柱投影。如果椭圆柱面与赤道相切，此时称为正轴圆柱投影；如果与某一经线圈相切，则称为横轴圆柱投影。

按变形的性质划分，圆柱投影可分为等角、等面积和等距离投影，墨卡托投影就是正轴等角圆柱投影。

1 横轴墨卡托投影

常见的高斯克吕格投影是横轴墨卡托投影的一种，由于高斯-克吕格公式仅适用于沿子午线分布的狭长地带的投影，才能保证其投影变形很小，故其进行投影时常常按需要进行分带[1]。

高斯投影6°带：自0°子午线起每隔6°经差自西向东分带，依次编号1,2,3,…，用N表示带号，L表示中央子午线经度，则带号与中央子午线经度关系：L=6N-3，我国东西跨度比较大，中央子午线经度由75°起至135°，共计11带（13～23带）。

高斯投影3°带：它的中央子午线一部分同6°带中央子午线重合，一部分同6°带的分界子午线重合，用N表示带号，L表示中央子午线经度，则带号与中央子午线经度关系：L=3N。我国3°带由72°起至135°，共计22带（24～45带）。

2 斜轴墨卡托投影

有些地区的伸展方向既不沿纬线也不沿经线，其区域中心线在地球上像一个斜向的大圆，这种情况下可采用斜轴墨卡托投影。此时，圆柱与投影区域中心线对应的球面上大圆相切，其尺度因子为1[2]。斜轴墨卡托投影的中心线是大地线，圆柱与选定投影区域中线对应的大圆相切。斜轴墨卡托投影是正形投影，投影长度比与到对应中心线的大圆的距离有关，但在任何点上长度比在各个方向上保持恒定。

3 投影转换

投影转换是在两种不同性质的投影平面上进行的，其上的点位可以按如下的对应关系式来表示：

式中，X、Y是新地图投影平面上的直角坐标，而x、y是需要变换的原地图投影平面上的直角坐标。而对于两种投影，其原始函数可表达为：整个地图变换的流程可表述为：

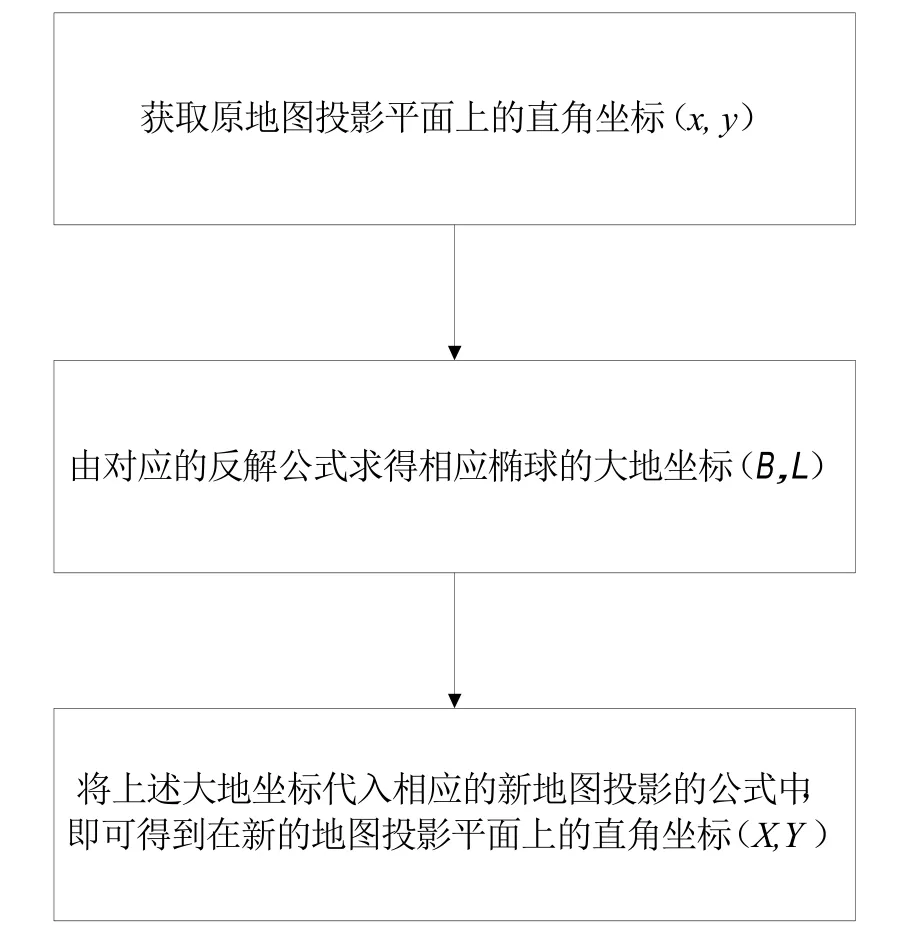
将原地图投影的反算坐标表示为：

则地图投影的通用数学公式可表述为：

对于投影公式已知的投影，一般均可根据上述公式进行相应转换。

本文以某处大比例尺地形图为例，根据投影转换的原理基于VB平台[3]编制程序，对autocad进行二次开发[4]，展示两种投影方式的转换。

图1 原横轴墨卡托投影下地形图

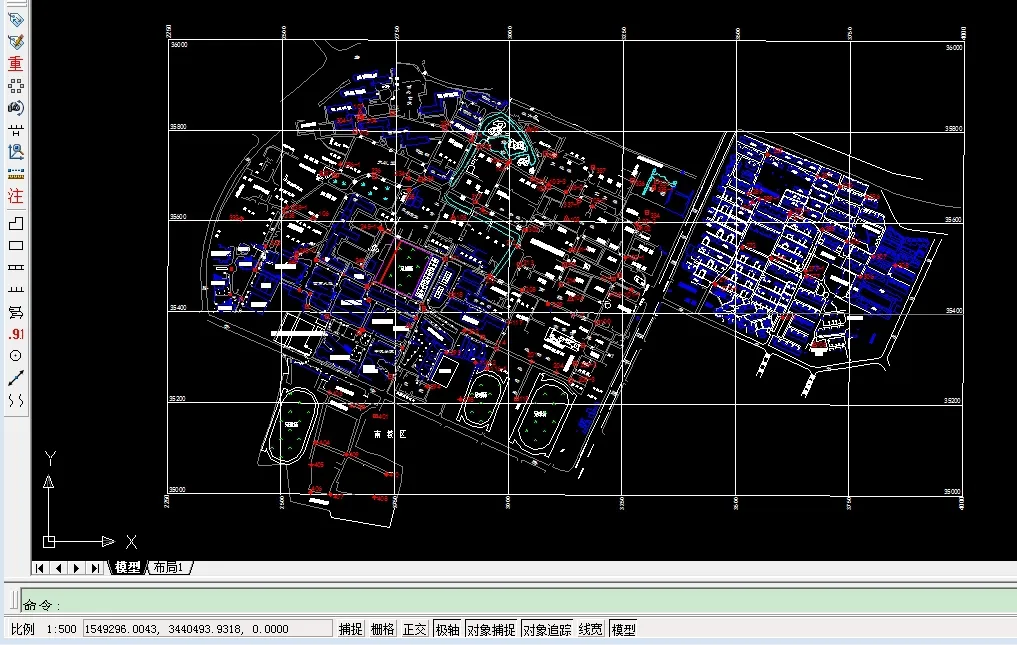
图2 转换后斜轴墨卡托投影下地形图

图3 转换后X方向差值图

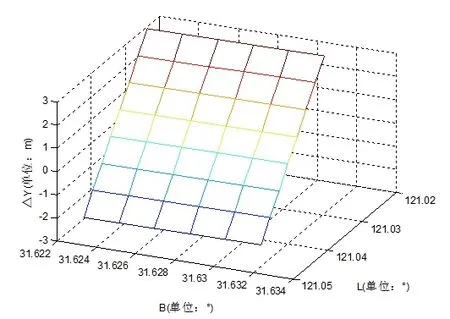
图4 转换后Y方向差值图

对于以上两种投影方式，由于均为等角投影，单从视觉的角度很难发现其中的差异，本文选取网格上8×6个点为特征点，分别获取其两种投影方式下的平面坐标，比较其变化情况，并以原投影中的平面坐标反算的B、L值分别做为X轴和Y轴，平面坐标差值为Z轴，同时由于差值图只是为反映X值和Y值的变化情况，所以在X和Y方向上都减去了一个常数。变化情况如下图所示：

4 结论

本文利用VisualBasic对AutoCAD进行二次开发进而实现了这两种地图投影的变换，以大比例尺地形图为例展示了不同投影方式显示地图的差异，可以方便地实现地图投影的转换。

[1]孔祥元，梅是义.控制测量学 [M].北京：测绘出版社，1991

[2]胡毓钜等.地图投影 [M].北京：测绘出版社，1981

[3] （美）斯蒂芬斯 (Stephens,R.)著；徐燕华译.Visual Basic 2008编程参考手册 [M].北京：清华大学出版社，2002

[4]陈俊平，王解先.用VB实现对AutoCAD图的转换 [J].测绘通报.2006，（3）：52～53

P217[文献码]B

1000-405X（2016）-5-176-2

许冰（1982～），男，研究生，工程师，研究方向为工程测量及地下管线探测方向的应用研究。