重力对空间相机系统波像差影响的光机集成分析与验证

董得义，李志来，薛栋林，陈长征，张学军

(中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033)



重力对空间相机系统波像差影响的光机集成分析与验证

董得义*，李志来，薛栋林，陈长征，张学军

(中国科学院 长春光学精密机械与物理研究所，吉林 长春 130033)

对空间离轴相机在重力载荷作用下的系统波像差变化进行了集成仿真分析，同时研究了分析结果的精度。介绍了集成仿真分析技术的基本流程和关键技术，对比分析了ZERNIKE多项式拟合法与形函数插值法两种面形畸变转换接口算法的优劣。介绍了常用的两种形函数构造方法的基本原理，基于面积法构造形函数得到了光学元件面形畸变的接口文件。最后，在相机的光机结构装调完毕后，对系统波像差在重力载荷作用下的变化进行了测试。测试结果表明，该空间相机3个视场系统波像差的变化量分别为0.029 8λ(-1视场)、0.019 4λ(0视场)、0.052 3λ(+1视场)，与分析结果基本吻合。3个视场分析结果的误差分别为0.002 4λ(-1视场)、-0.000 9λ(0视场)、0.007λ(+1视场，)均小于0.01λ，满足工程设计的要求，验证了集成仿真分析结果的准确性。此外，通过集成分析技术定量得到了不同影响因素对系统波像差的影响，基于此优化设计光机结构，改善了重力对空间相机3个视场系统波像差的影响。

空间相机；波像差；光机集成分析；重力变形

*Correspondingauthor,E-mail:s200201029@163.com

1　引　言

在空间相机的设计中，地面环境与空间环境(简称：地空环境)的差异对空间相机成像质量的影响较大。地空环境差异主要有微重力环境、电磁辐射环境以及空间热环境。对于结构设计，微重力环境下的自重释放对空间相机成像质量的影响是需首要解决的问题[1]。

所谓自重释放是指空间相机在地面1g的重力场内完成了加工、装配和制造；入轨后，由于重力场几乎为0，导致空间相机结构件在地面重力场内的变形出现了反弹，引起光学元件的面形发生畸变以及不同光学元件之间的相对位置发生了变化，这些变化会影响相机的成像质量。

在方案设计阶段，自重释放对相机结构件的影响，一般通过仿真分析的方法获得，当前的设计思路为：首先，采用光学设计软件给出光学系统的稳定性公差指标，然后对相机进行自重变形分析，将各光学元件面形畸变及相对位置变化分析结果与稳定性公差指标进行对比，若分析结果小于稳定性公差指标要求，且具有一定的安全裕度，则认为方案满足设计要求；反之，则需要对结构进行优化直到分析结果满足指标要求为止，通常将这种方法称为指标分配法[2]。

常用的光学系统设计软件如CODEV和ZEMAX，都具有强大的分析功能，能够针对光学系统中每个光学元件的变形量(包括面形畸变及相对位置变化)对成像质量(MTF、波像差等)的影响进行灵敏度分析，再结合分配给系统稳定性对MTF产生的影响量的指标，就可以制定出光学系统的稳定性公差[3]。

在稳定性公差指标的制定过程中，空间相机的结构特性如同一个黑匣子，不清楚哪些因素变化大，哪些因素变化小，这就要求制定出的稳定性公差要包络可能出现的最恶劣的情况，即使光学系统中每个光学元件的每个变化量都取稳定性公差的允许变化量的上限进行耦合，其对光学系统的成像质量的影响都要满足设计要求，这会导致采用这种方法制定的稳定性公差指标过于严格。

现实中，空间相机的结构形式选定以后，每个影响因素都同时变化很大的可能性较小，常见的情况是，在所有影响因素中，大部分的影响因素都满足设计指标要求，而且都比设计指标小很多，但个别的因素略大于设计要求，则这个方案是否可行很难判断；其次，所有影响因素都满足设计要求，但有多个因素的变化量已经非常接近设计指标了，那么这个方案的是否可行，这些问题都是指标分配法无法回答的。光机集成仿真分析技术可解决这样的问题。

光机集成分析与指标分配法的思路相反，在光机集成分析中，相机的结构形式是选定的，其在重力作用下的变化量可通过结构分析获得，只要把各光学元件的变形结果直接代入到光学设计软件中，通过对比代入前后的光学性能指标变化，就可以直接评价当前设计方案在重力载荷作用下的变形量是否满足设计要求。这种评价方式绕开了与稳定性公差指标的对比，更加直接、准确和全面。

Sigfit商用集成仿真分析软件的出现，标志着集成仿真分析技术在国外从算法到应用上都已非常成熟[4-7]。在国内关于集成仿真分析的论文较多，但国内的论文主要集中在接口程序算法的讨论上，关于其在工程项目中的运用[8-9]和其分析结果的精度进行分析讨论的论文较少。

本文以某空间离轴相机为例，对其在自重载荷作用下系统波像差的变化量进行了集成仿真，并在相机装配完毕后，对重力导致的影响进行了测试，测试结果表明集成仿真分析结果的精度能够满足工程要求。

2　集成仿真分析技术

2.1基本流程与关键技术

空间光学相机的集成仿真技术通常是指光、机、热3个学科的集成仿真分析，是以光学分析、热分析和结构分析的单学科计算为基础，通过数据转化，此学科计算结果可以作为另一学科的边界约束条件，达到各学科的集成分析计算，其关系如图1所示[10]。

图1　集成分析流程Fig.1　Optomechnical analysis interaction

通过结构分析软件能够得到空间相机在外载作用下，各光学元件的相对位置变化及面形畸变。相对位置变化移包括相对倾角变化和相对线量变化，这两种变化属于刚体位移变化，在光学分析软件中可以直接将相对位置的变化量代入到光学设计模型中，从而评价相对位置变化量对光学系统成像质量的影响；光、机集成分析技术的主要难点是把光学元件面形畸变转化成光学分析软件可接受的数据文件。一种是采用ZERNIKE多项式拟合的方式获得前37项ZERNIKE多项式的系数，并将该37项系数耦合到原始系统中，修正原始系统，得到变形后的系统，进而评估光学系统在外载荷作用下的性能[11-13]；另一种是采用形函数插值的方法[14]，获得面形变形后的插值文件(.INT文件)，同理，可将该.INT文件代入原光学系统中，同样可以对该面形的变化对光学系统的影响进行评价。

由于Zernike多项式在单位圆且连续的空间域上是正交的，在满足正交性的条件下，Zernike多项式是有效的光机数据转换工具；但在实际应用中，TMA系统的反射镜通常为长条形，而且通过有限元法得到的光学表面的变形数据都是离散的，研究表明，离散点的数量越大正交性越好，离散点数目越少，正交性越差[15-16]；这就导致了Zernike多项式的正交性非常差，而使拟合结果精度降低。

干涉图插值法成功解决了上述问题，尤其是针对离轴三反系统的光机集成分析，已经基本取代Zernike多项式拟合的方法，成为最主要的接口转换工具。

2.2干涉图插值法的基本原理

干涉图插值法流程为：首先读取有限元法计算得到的镜面节点变形数据，进行坐标变换，计算刚体位移，再根据公式对变形数据进行处理，将镜面节点的变形结果由笛卡尔坐标系转换为基于表面法向坐标系下的数据形式，然后根据不同的算法，通过栅格点附近的镜面节点的变形数据对该栅格点进行插值，这样就得到了类似于干涉图数据的采用均匀栅格点描述的面形变化数据(.INT文件)。

形函数法[17]是目前实体插值领域最重要的一种算法，是有限元分析的重要基础，具有以下性质：

(1) Kronecker delta性质：在结点上插值函数的值有：

(1)

(2) 归一性：在单元中任一点各插值函数之和应该等于1；

(3) 连续性：相邻单元在公共边界上的位移要具有连续性。

形函数的构造方法通常有面积法和等参单元法。

a) 面积法构造形函数

首先，采用Delaunay算法对镜面节点进行三角剖分(Delaunay三角剖分(DT)是目前最为通用的全自动网格生成算法之一，它可以将平面内离散点划分为有限个三角形，并且保证运算收敛，然后对每一个三角形构成一个线性插值单元(如图2所示)，利用三个顶点的变形量采用形函数法，即可求出每个三角形区域内每个栅格点的变形。

图2　均匀网格点位于三角形单元内部Fig.2　Uniform grid lies in triangle element

采用面积法构造形函数的基本过程为：任取如图3所示的平面三角形，节点逆时针分别为A(XA,YA)、B(XB,YB)、C(XC,YC)，任意待求点为P(XP,YP)，A、B、C点样本值分别为UA、UB、UC，待求P点的值为UP，如图3所示。

图3　三角形单元的面积坐标Fig.3　Area coordinates of triangle element

根据上图ΔABP、ΔBCP、ΔCAP的面积分别为T1、T2、T3，有：

SΔABC=T1+T2+T3,

(2)

两边分别除以SΔABC，则：

(3)

可定义A点的相对面积变量SA为：

(4)

当P点与A点重合，此时SA=1，当P点与B、C点重合时，SA=0。同样可以B、C点。因此三角形的形函数可以表示为：

UP=UASA+UBSB+UCSC,

(5)

式中:SB、SC分别为：

(6)

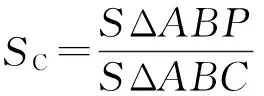
(7)

三角形的面积可以根据3个顶点的坐标求出，以SΔABC的面积求解为例：

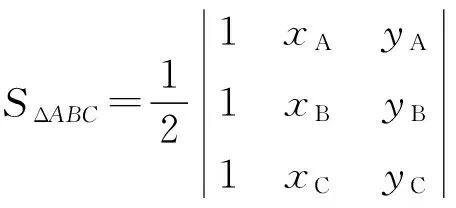
(8)

b)等参单元法构造形函数

在等参单元法中通常要用到笛卡尔坐标系和自然坐标系。笛卡尔坐标系用x,y,z表示，自然坐标系用一组不超过1的无量纲参数r,s,t表示，边界点分别对应自然坐标等于1或-1的点。等参单元法的基本思想是将笛卡尔坐标系中不规矩的线段、平面多边形、空间多面体转换为标准的自然坐标系上线段、平面多边形、空间多面体，在自然坐标系建立插值方程，实现在笛卡尔坐标系中的插值方程。

c)两种形函数构造法的对比

采用面积法构造形函数是针对三角形单元进行插值运算，而等参单元构造形函数是针对四边形单元进行插值运算。由于采用Delaunay算法可以由离散点生成三角形单元，因此在面积法构造形函数进行的插值运算中，只需要结构分析提供节点编号及每个节点的变形量；若采用等参元法构造形函数，除提供节点编号及每个节点的变形量外，还要提供镜面的单元信息；而且，在实际工作中，镜面的单元类型一般都是三角形单元与四边形单元混合出现的，因此，即使采用等参元法构造形函数，在遇到三角形单元的局部区域，也要采用面积法构造形函数，因此在实际应用中，面积法构造形函数更为方便。

2.3干涉图插值法的误差分析

与Zernike多项式拟合相比，干涉图插值法避免了由于数据离散和光学表面形状等因素导致的拟合误差，适用于各种形状的镜面的面形分析，影响其精度的主要因素为[14]：

a) 计算刚体位移时的拟合误差；

b) 数据处理引入的误差；

c) 由有限元网格点插值到均匀干涉点处的插值误差；

d) 干涉图数据导入到光学软件后，光线追迹时入射光线的入射点位置不能刚好为均匀栅格点位置，需再次插值，从而引入另一个插值误差。

当均匀栅格点的密度较高时，插值引入的误差很小，能够满足大多数光学系统的集成分析要求。

3　光机集成分析

3.1空间相机设计方案介绍

某空间相机采用离轴三反TMA[18]、无中心遮拦、无中间像的光学系统，光学系统包括主镜、次镜和三镜等，为了使光学系统结构设计更为紧凑，在像面和三镜之间加入平面反射镜，起到折叠光路作用。

光学系统结构如图5所示，除次镜的镜面为圆形外，主、三镜都为长条形。

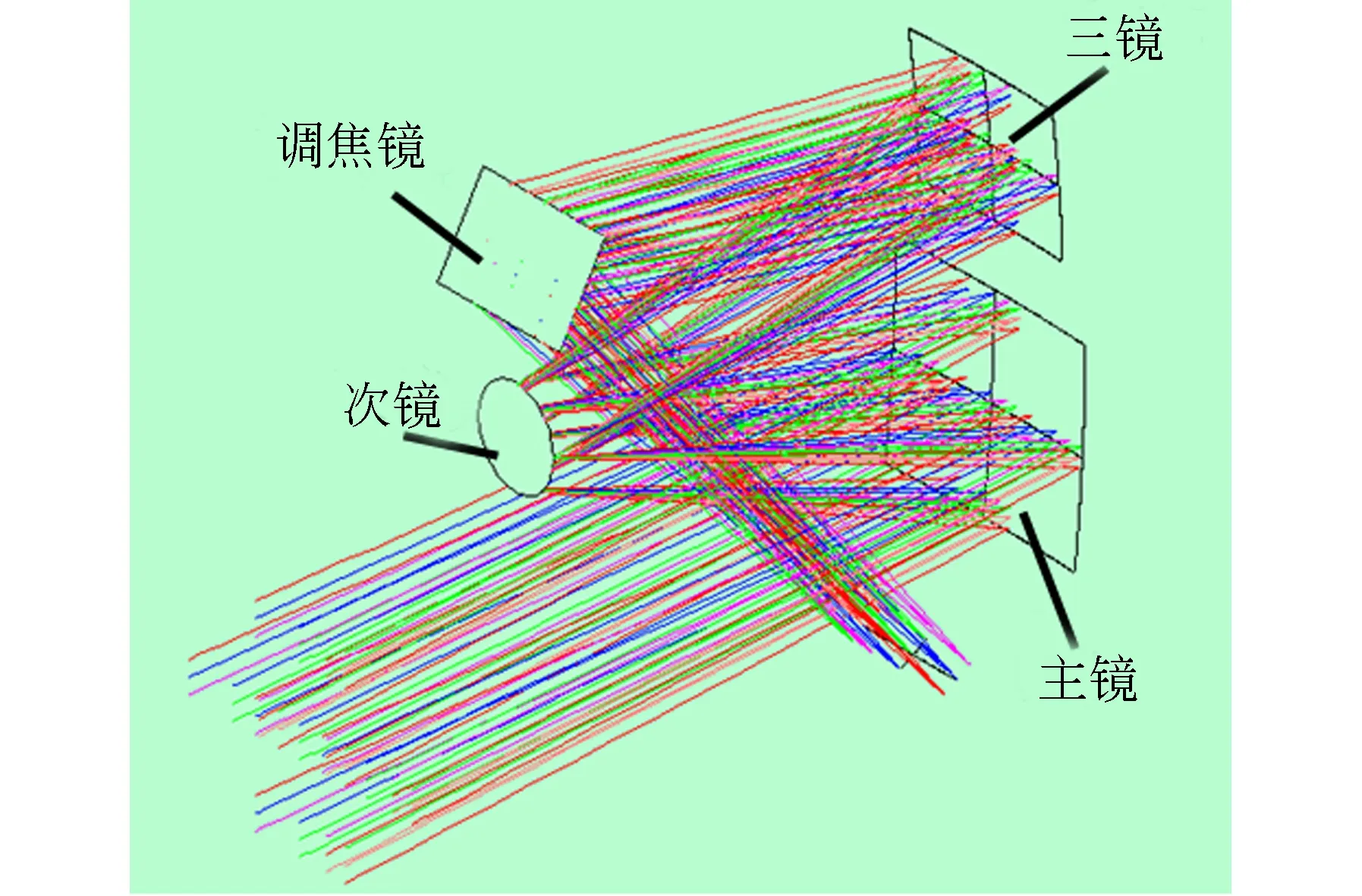
图5　离轴三反光学系统Fig.5　Configuration of off-axial TMA optical system

图6　结构设计方案Fig.6　Layout of structure design

相机的光机结构如图6所示。有限元模型如图7所示。

图7　有限元模型Fig.7　Finite element model of camera

坐标系定义：X向为相机在装调过程中的重力方向，Z向为光轴方向，Y向由右手定则确定；坐标原点为次镜镜面中心，如图8所示。

图8　坐标变换后两套模型的空间关系Fig.8　Space relation between the two model after coordinate transformation

相机状态定义，相机在自重变形测试试验中，主要有0°状态和180°状态。在0°状态下相机受+x向重力；在180°状态下相机受-x向重力，由于两个状态中，相机结构受到的重力大小相等，方向相反，因此，相机在地面翻转180°试验中，要考虑各光学元件之间2倍地面重力引入的变形[12]。

3.2集成分析

1)坐标变换

将Patran有限元模型的坐标系调整成与CODEV光学模型的坐标系一致(包括：坐标轴方向的定义及坐标原点位置的定义)，经坐标变换后，有限元模型与光学系统模型在同一坐标系内能完全重合，如图8所示。

2)结构仿真分析计算

采用结构仿真分析软件MSC.Patran/Nastran计算结构在-x向2倍自重载荷作用下的变形，分析结果如表1所示，空间相机位移变形云如图9所示。

表1　自重变形分析结果

图9　自重载荷位移变形云图Fig.9　Displacement plot of gravity deformation

3)集成分析

集成仿真分析应分步进行，这样可以得到每一个影响因素的变化量对系统波像差的定量的影响，分析结果如表2所示。

表2　分步集成分析结果

4)分析结果总结

通过分步集成的分析结果，对每个光学元件的每个变形量对系统波像差的影响进行了定量的分析。

a) 主镜镜面的面形变化对2个边缘视场系统波像差的影响最大都超过了0.02λ，对中心视场的影响较小；

b) 次镜相对于主镜相对位置的变化对+1视场与中心视场系统波像差的影响都超过了0.01λ，对-1视场的影响较小；

c) 次镜面形变化对系统波像差影响较小，可忽略不计；

d) 三镜面形及相对位置变化都对系统波像差的影响都接远小于0.01λ，可忽略不计；

e) 主镜镜面的面形变化对系统波像差的影响最大，次镜相对于主镜的刚体位移次之，三镜的影响可忽略。

4　试验测试与对比分析

4.1试验测试

在空间相机光学镜头与框架集成完毕后，为了检测重力对相机成像质量的影响，对相机镜头进行了翻转试验[19]，翻转试验的过程为：1)测试相机在0°状态下3个视场的系统波像差；2)将相机绕光轴旋转180°，测试相机在180°状态下3个视场系统的波像差。

两种状态下，空间相机3个视场系统波像差检测结果对比如图10～12所示。

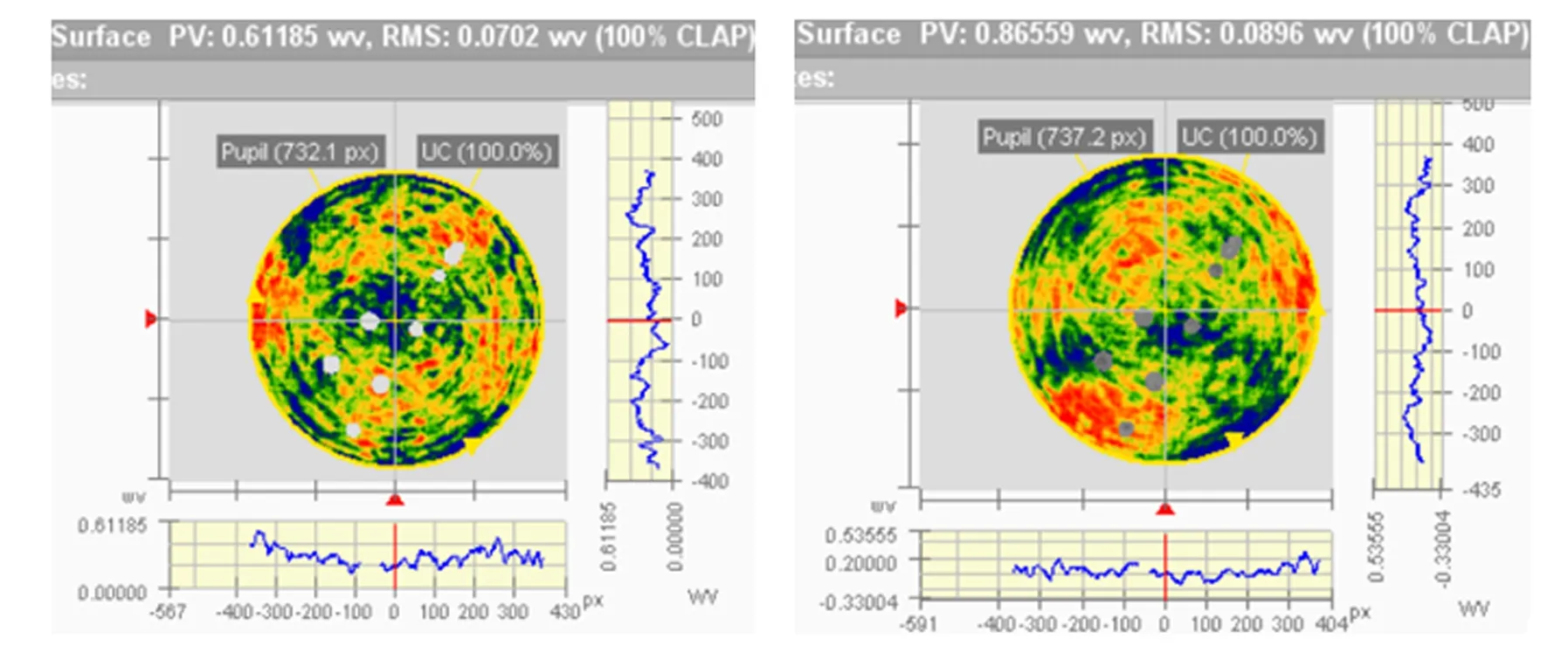
(a)0°　　　　　　　　　(b)180°图10　0视场检测结果Fig.10　Test result of 0 field of view

(a)0°　　　　　　　　　(b)180°图11　-1视场检测结果Fig.11　Test result of -1 field of view

(a)0°　　　　　　　　　(b)180°图12　+1视场检测结果Fig.12　Test results of +1 field of view

3个视场系统波像差在翻转180°前后检测结果如表3所示。

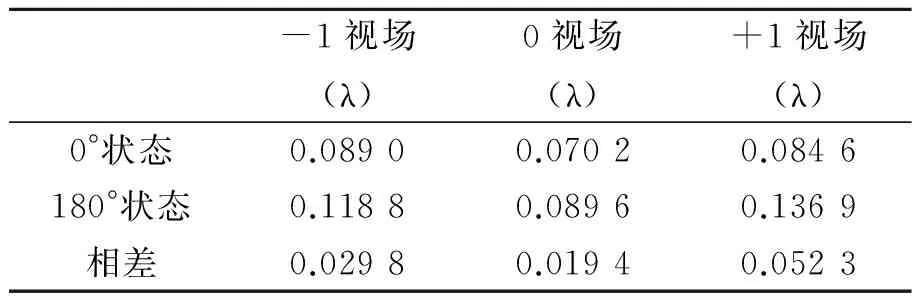
表3　检测结果统计

由表3可知，+1视场系统波像差变化最大，达到了0.052 3λ，远超过设计指标小于0.01λ的要求；-1视场系统波像差变化量也远大于设计指标的要求，接近0.03λ；中心视场变化量最小，但也不满足设计指标的要求；对比+1视场与-1视场的检测结果，可以发现结构的变化具有明显的不对称性，+1视场的变化量远大于-1视场的变化量。

4.2对比分析

3个视场系统波像差在翻转前后变化量的分析结果与测试结果对比如表4所示。

表4　分析结果与测试结果的对比

3个视场变化量分析结果与测试结果的最大误差为0.007λ，小于0.01λ，能够满足工程设计对分析精度的要求；

3个视场变化量的分析结果也体现除了+1视场变化量最大，中心视场变化量最小的特征，在分布趋势上也与实测结果吻合；

5　优化设计与验证

分步集成的分析结果表明，导致空间相机在重力载荷作用下，系统波像差变差的主要因素为主镜镜面的面形变化和次镜相对于主镜的刚体位移变化，这为结构的优化设计明确了方向。首先，对主镜组件的结构进行了优化设计，主要调整了镜体的结构参数、优化了镜体轻量化孔的形状以及支撑点的数量和位置，优化后，主镜组件自身在重力载荷作用下的面形变化从22 nm减小到12 nm；其次，对相机的主支撑结构也进行了优化设计，针对相机装调方向重力的加载方向，主要调整了支撑框架结构横向的抗弯刚度，经过对主框架的优化设计，次镜相对于主镜的倾角变化从12.6″减小到8.3″；优化设计后，主镜以及次镜对系统波像差的影响的到了明显的改善，与优化前影响量的分析结果对比如表5所示。

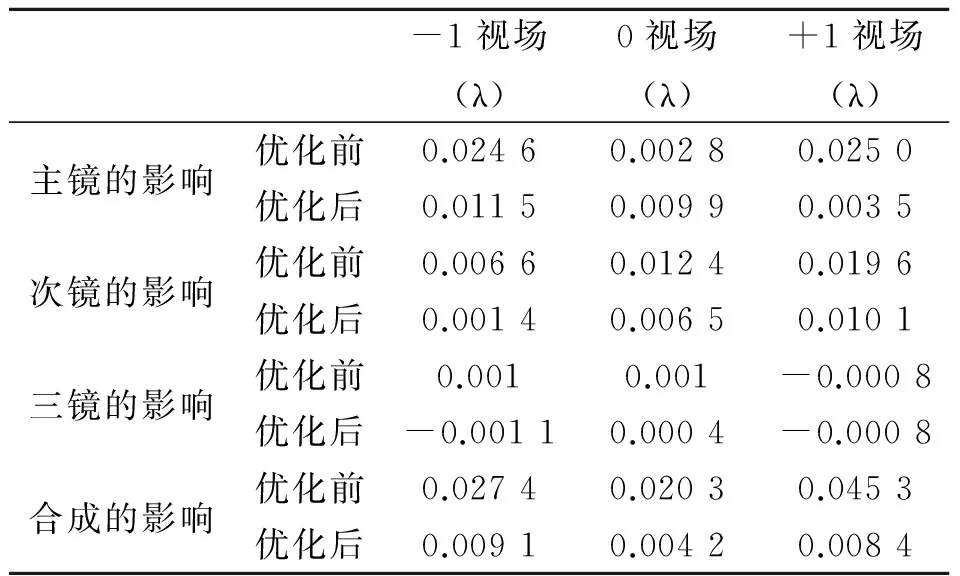
表5　优化前后分析结果的对比

经优化设计后，主镜与次镜对系统波像差的影响得到了明显的改善，整个系统在重力载荷作用下，3个视场系统波像差的变化量也都小于0.01λ，能够满足设计指标的要求。

新的光机结构装调完毕后，也进行了翻转180°的试验，试验结果如表6所示。

表6　优化设计后测试结果

试验结果表明：经过优化设计，空间相机在重力载荷作用下，系统波像差变化量测试结果的变化量都小于0.01λ，与分析结果基本吻合。证明了通过光机集成分析方法对问题原因的定位准确，制定的改进措施有效，从而进一步验证了集成分析方法的准确性。

6　结　论

本文首先对光机集成仿真分析中的关键技术进行了研究，针对反射镜为长条形以及有限元模型中镜面结点离散性较强的特点，提出了干涉图插值法是TMA空间相机进行光机集成分析中接口转换工具的首选。

其次，采用光机集成仿真分析技术对某空间TMA相机在重力载荷作用下，系统波像差的变化量进行了仿真分析，通过分步集成，得到了每个影响因素对系统波像差的定量的影响。并在相机装调完毕后，对重力导致系统波像差的变化进行了试验测试，测试结果表明：3个视场系统波像差变化量的误差分别为0.002 4λ(-1视场)、-0.000 9λ(0视场)、0.007λ(+1视场)都小于0.01λ，能够满足工程设计的要求，验证了集成仿真分析结果的准确性。

最后，根据分步集成分析中确定的主要因素，对主镜组件的结构以及支撑框架的结构进行了优化设计，优化设计后的试验结果表明：集成仿真分析技术对问题的定位准确，提出的优化措施有效，很好的解决了原始结构中出现的问题。

本文通过工程实例验证了光机集成仿真分析技术的准确性，以及与指标分配法相比在实际应用中的优越性，尤其是针对未来指标更严、公差较小的长焦距、大口径的光学系统，集成仿真分析将会取代指标分配法成为工程分析中的主流。

[1]刘磊，马军，郑玉权．空间微重力下离轴三反相机调焦范围[J]．中国光学，2015，7(2)：320-325．

LIU L，MA J， ZHENG Y Q. Defocus range if off-axis three mirror anastigmat(TMA) camera under space microgravity [J].ChineseOptics，2015，7(2)：320-325．(in Chinese)

[2]杨怿，陈时锦，张伟．空间光学遥感器光机集成分析技术综述[J]．光学技术，2005，31(6)：913-918．

YANG Y，CHEN SH J， ZHANG W. Review of thermal-structure-optical integrated analysis of space remote sensor[J].OpticalTechnique，2005，31(6)：913-918．(in Chinese)

[3]王孝坤．一种高分辨力空间相机的光学设计[J]．光学学报，2015，35(1)：0122001．

WANG X K. Optical design of a high resolution space camera[J].Actaopticasinica，2015，35(1)：0122001．(in Chinese)

[4]ALSON E. Hatheway. An overview of the finite element method in optical system [J].ProceedingsofSPIE, 1991, 1532：2-14.

[5]VICTOR G, GREGORY M. Making FEA results useful in optical analysis[J].ProceedingsofSPIE, 2002, 4769：24-33.

[6]KEITH B. DOYLE. Numerical methods to compute optical errors due to stress birefringence[J].ProceedingsofSPIE, 2002, 4769：34-42.

[7]KEITH B. DOYLE, VICTOR L. Integrated Optomechanical analysis of adaptive optical systems[J].ProceedingsofSPIE, 2004, 5178：20-28.

[8]杨怿，张伟，陈时锦．光机热集成分析中数据转换接口的研究[J]．宇航学报，2005，26(2)：201-206．

YANG Y，ZHANG W，CH SH J. Study on data transmission tool for thermal/structural/optical integrated analysis [J].JournalofAstronautics，2005，26(2)：201-206．(in Chinese)

[9]刘家国，李林．光机热集成分析中数据转换接口研究[J]．北京理工大学学报，2007，27(5)：427-431．

LIU J G，LI L. Study on the data transfer interface in the thermal/structural/optical integrated analysis[J].TransactionsofBeijingInstituteofTechnology，2007，27(5)：427-431．(in Chinese)

[10]KEITH B. DOYLE，VICTOR L.IntegragtedOptomechanicalAnalysis(secondedition)[M]. Bellingham Washington：SPIE Press，2012：2．

[11]李贤辉，吴清文，杨洪波．光学工程分析中的镜面面形处理新方法[J]．光学技术，2003，29(6)：752-754．

LI X H，WU Q W，YANG H B. New method of mirror surface figure treatment in optical engineering analysis [J].OpticalTechnique，2003，29(6)：752-754．(in Chinese)

[12]李福，阮萍，马小龙，等．用Zernike多项式实现光机分析的技术方法[J]．应用光学，2007，28(1)：38-42．

LI F，RUAN P, FENG X L,etal.. Methods of opto-mechanical analysis with Zernike polynomials[J].JournalofAppliedOptics，2007，28(1)：38-42． (in Chinese)

[13]张伟，刘剑锋，龙夫年，等．基于Zernike多项式进行波面拟合研究[J]．光学技术，2005，31(5)：675-678．

ZHANG W，LIU J F, LONG F N,etal.. Study on Wavefront fitting using Zernike polynomials[J].OpticalTechnique，2005，31(5)：675-678． (in Chinese)

[14]刘勺斌，杨洪波．一种用于光机热集成分析的新方法-干涉图插值法[J]．应用光学，2007，28(5)：553-558．

LIU SH B，YANG H B. New data transform method for thermal/mechnical/optical integrated analysis: interferogram interpolation [J].JournalofAppliedOptics，2007，28(5)：553-558． (in Chinese)

[15]KEITH B D，VICTOR L G，GREGORY J.IntegragtedOptomechanicalAnalysis(secondedition)[M]. Bellingham Washington：SPIE Press，2012：69-72，74．

[16]鄢静舟，雷凡，周必方，等．用Zernike多项式进行波面拟合的集中算法[J]．光学 精密工程，1999，7(5)：119-128．

YAN J ZH，LEI F, ZHOU B F，etal.. Algorithms for wavefront fitting using zernike polynomial [J].Opt.PrecisionEng.，1999，7(5)：119-128. (in Chinese)

[17]王勖成．有限单元法[M]．北京：清华大学出版社，2003：58-59.

WANG X CH.FiniteElementMethod[M]. BeiJing: QingHua University Press，2003：58-59. (in Chinese)

[18]沙巍，陈长征，许艳军，等．离轴三反空间相机主三镜共基准一体化结构[J]．光学 精密工程，2015，23(6)：1612-1619．

SHA W，CHEN CH ZH，XU Y J，etal.. Integrated primary and tertiary mirror components from common base line of off-axis TMA space camera[J].Opt.PrecisionEng.，2015，23(6)：1612-1619. (in Chinese)

[19]张星祥，任建岳．TMA空间相机性能稳定性的全状态分析与测试[J]．红外与激光工程，2014，43(9)：2996-3004．

ZHANG X X，REN J Y. Analysis and testing on imaging-performance stability of TMA space camera at various states [J].InfraredandLaserEngineering，2014，43(9)：2996-3004. (in Chinese)

董得义(1979-)，男，天津人，博士，副研究员，2002年、2005年于北京工业大学分别获学士、硕士学位，2012年于中科院长春光学精密机械与物理研究所获得博士学位，主要从事空间光学遥感器有限元分析、结构优化设计、力学试验等方面的研究工作。E-mail: s200201029@163.com

李志来(1965-)，男，汉族，吉林镇赉人，研究员，1986年于吉林工学院获得学士学位，主要从事空间光学遥感器结构技术及精密机械方面的研究。Email: lizl2004@sohu.com

(版权所有未经许可不得转载)

Integrated optomechanical analysis and experiments for influence of gravity on wavefront aberration of space camera

DONG De-yi，LI Zhi-lai，Xue Dong-lin，CHEN Chang-zheng，ZHANG Xue-jun

(ChangchunInstituteofOptics,FineMechanicsandPhysics,ChineseAcademyofSciences,Changchun130033,China)

The variation of the wavefront aberrations of a Three-mirror Anastigmat(TMA) space camera under gravity was analyzed by integrated analysis method and the analytical accuracy was discussed. The basic process and key technology of the integrated analysis method were introduced, two kinds of surface distortion conversion interface algorithm (ZERNIKE polynomial fitting method and shape function interpolation method) were compared. Then, the principles of two kinds of shape functions were introduced, and the interface file of the optical element surface distortion was obtained by the area coordinate method. Finally, the variations of wavefront aberrations in gravity load were tested after the camera alignment was completed. Test results show that the variations of the wavefront aberrations of the three fields of view are respectively: 0.029 8λ(-1), 0.019 4λ(0), and 0.052 3λ(+1), which are agreement with that of the analysis results. The errors of the analysis results of the three fields of view are respectively 0.002 4λ(-1), -0.000 9λ(0), 0.007λ(+1), all less than 0.01λ, meet the requirements of engineering and verify the correction of the integrated analysis method. Meanwhile, the quantitative effects of each factor on the system wavefront aberrations were obtained by the integrated analysis method. On the basis of the optimization design with the integrated analysis method, the influences of gravity on wavefront aberrations of the three fields of view of the space camera is significantly improved.

space camera; wavefront aberrations; integrated optomechnical analysis; gravity deformation

2015-12-11；

2016-01-20.

国家863高技术研究发展计划资助项目(No.2009AA7020107)；

1004-924X(2016)08-1917-10

V447.3；TP391.9

A

10.3788/OPE.20162408.1917