冷变性特征值的选取及应用

李 悦，张煜欣

（国家知识产权局专利局专利审查协作湖北中心，湖北武汉，430070）

冷变性特征值的选取及应用

李 悦，张煜欣

（国家知识产权局专利局专利审查协作湖北中心，湖北武汉，430070）

当齿轮产生裂纹时，其啮合刚度变化引起的振动响应特征是实现裂纹故障诊断的重要依据。建立含有齿根裂纹故障的齿轮传动系统的8自由度动力学模型，利用龙格库塔法求解；在对求得的故障响应取多种特征值，通过对比比较选出具有冷变性的特征值。测试不同裂纹情况下不同转速的振动的故障响应，试验结果与数值分析结果相符，为齿轮传动裂纹故障诊断提供了理论基础。

冷变性；动力学方程；故障诊断

0　前言

故障预测对于预知处于工作状态的部件因突然失效而导致的灾难的发生有很重要的意义。故障预测特征选择方法是实现故障预测功能的关键，它决定了故障预测的准确和有效。

近些年来，很多学者对提取的故障的预测特征值进行了一些研究。浙江大学的曹志彤等人，利用小波系数诊断电机故障。华北电力大学的辛卫东研究在经典振动信号分析。本文将齿轮看作一个振动系统，对其建立各种相应的动力学模型，获得各种状态下的齿轮振动仿真信号，运用时域法，寻找时域响应的波形指标等，然后分析特征值与齿轮工作状态之间的关系，提取对故障敏感而与工况无关的特征参数，并通过试验验证。本文中定义具有这类特性的特征值的性质为冷变性。

1　齿轮时变啮合刚度计算

本文用能量法对含齿根裂纹故障的齿轮的时变啮合刚度（TVMS）进行计算。

2　齿轮系统的动力学模型建立

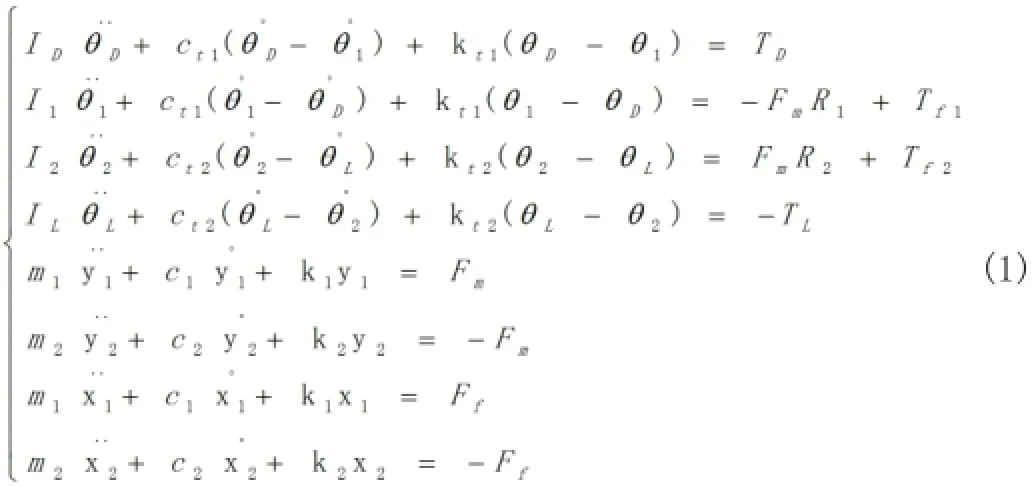
齿轮的动态响应可以通过动态总成参数建模来提取。

齿轮的动力学模型建立如下公式（1）：

时变啮合力可表示为

时变摩擦力可以表示为

3　带齿根裂纹的动态响应与不同程度齿根裂纹响应的特征值提取

3.1带齿根裂纹的动态响应提取

当齿轮箱输入轴转频为600r/min时，故障特征频率大小为10Hz。采用龙格库塔法求解动力学微分方程，响应值的时域波形如图 1 所示：

图1　25%裂纹动力学响应

图 1所示的裂纹程度为25%的响应信号图，可以观察到故障裂纹以0.1s的周期出现，频率为故障齿轮所在轴的转频10Hz，记为。将图1局部放大，可以看到齿轮啮合一周所出现的20个啮合周期，每个啮合周期大小为0.005s，如图 2 所示。即齿轮啮合时会出现一个相对较大的冲击，这个周期出现的频率为啮合频率，大小为200Hz记为。由于转频对于啮合频率是一个调频过程，所以对齿轮的动态响应做FFT后不仅可以观察到啮合频率及其倍频，如图3所示，而且还能在啮合频率的周围会存在边频带，这些边频带的出现与主动轮的转频有关对于带裂纹的齿轮啮合响应做包络谱，如图4所示，可以发现齿轮啮合时的转频及其倍频。

图2　带裂纹齿轮啮合动力学响应放大效果图

图3　带裂纹齿轮啮合动力学响应的频谱图

图4　带裂纹齿轮啮合动力学响应的包络图

3.2不同齿根裂纹动力学响应在时域法中的特征值提取

特征值，比如均方值，是一种经常被用在状态监测和故障诊断的指标。本文采用均方值、波形指标、裕度指标和小波熵作为特征值。本文中，需要寻找一种满足冷变性的特征值。在360-840r/ min的情况下，根据裂纹程度，图5给出了计算所得的特征值以及比较结果。

从图5中可以看出，均方值、波形指标和小波熵这三种特征值对裂纹变化比较敏感。比较裂纹程度相同时候不同转速情况下三种不同特征值的值的大小情况，如表1所示：

表1　特征值参数在同种裂纹不同转速下的比较

从表格中可以知道，只有波形指标满足上文所说的冷变性条件，而均方值和小波熵虽然在对于裂纹的灵敏度和跟随性很好，但是其值大小在转数变化下变化很大。

图5　归一化的特征值值在不同转速和裂纹的情况下的比较

4　试验验证

试验设备中齿轮参数除了齿轮个数为37，其他参数不变，故障频率f1与仿真相同，啮合频率fe为370Hz。对信号进行EMD分解后，在第二个分量，图6中可以发现其波形与齿轮出现局部损伤故障时冲击信号波形非常相似。

因而，可以先对试验信号进行分解后再取其特征值，以获得更加明显的特征值。如图8所示，在10%～60%裂纹程度下，求不同转速下除去噪后的分量波形指标，比较结果如图：

可以发现，试验结果与仿真信号基本吻合。

5　结论

（1）建立齿轮传动系统的动力学模型，可以有效的揭示含裂纹的齿轮振动响应的机理。

（2）信号的众多特征值中存在一些具有冷变性特征的特征值，这些特征值在可以忽略转速的影响设备进行对状态监测和故障诊断的指标。

［1］ Wan Zhiguo，Cao Hongrui，Zi Yanyang，et al.An improved time-varying mesh stiffness algorithm and dynamic modeling of gear-rotor system with tooth root crack. Engineering Failure Analysis，2014，42：157-177.

［2］ Prashant Sondkar，Ahmet Kahraman.A dynamic model of a double-helical planetary gear set.Mechanism and Machine Theory，2013，70：157-174.

［3］ Feng Zhipeng，Zuo Ming J.Fault diagnosis of planetary gearboxes via torsional vibration signal analysis. Mechanical Systems and Signal Processing， 2013，36（2）：401-421.

［4］ Zhiguo Wan，Hongrui Cao，Yanyang Zi，Wangpeng He，Zhengjia He.An improved time-varying mesh stiffness algorithm and dynamic modeling of gear-rotor system with tooth root crack.Engineering Failure Analysis 2014， 42：157-17.

［5］ 万志国，訾艳阳，曹宏瑞，何正嘉，王帅.时变啮合刚度算法修正与齿根裂纹动力学建模.机械工程学报，2013，49（11）：153-160.

The selection and application of cold degeneration characteristic value

Li Yue，Zhang Yuxin
（Patent Examination Cooperation Hubei Center of The Patent Office，Wuhan Hubei，430070）

When gear crack is put forward，its mesh stiffness change caused by vibration response characteristics is the important basis to realize the crack fault.8 degrees of freedom dynamic model of gear transmission system with root crack fault was built using runge kutta method.A variety of characteristic values were obtained from the fault response. Select the characteristic value of cold denaturation by comparing different values.Test fault response of vibration in different rotating speed during different cases. The results of test are consistent with the results of numerical analysis， which provides a theoretical basis for the gear crack fault diagnosis.

cold degeneration characteristic value；dynamic model；fault diagnosis

图6　20%裂纹状态下的响应

图7　信号分解后的第二个分量的频谱图

图8　试验信号不同转速和裂纹程度情况下的波形指标

注：本文第二作者（张煜欣）对文章贡献等同第一作者。