基于MAPGIS的含量-面积分形法确定元素异常下限及圈定异常区：以湖南阳明山地区为例

崔玉良，王根厚，郎欣欣，曾志方

(1.北京探矿工程研究所，北京　100083；2.中国地质大学(北京)地球科学与资源学院，北京　100083；3.内蒙古自治区第十地质矿产勘查开发院，内蒙古 赤峰　024005；4.湖南省地质矿产勘查开发局四○九队，湖南 永州　425000；)



基于MAPGIS的含量-面积分形法确定元素异常下限及圈定异常区：以湖南阳明山地区为例

崔玉良1,2，王根厚2，郎欣欣3，曾志方4

(1.北京探矿工程研究所，北京100083；2.中国地质大学(北京)地球科学与资源学院，北京100083；3.内蒙古自治区第十地质矿产勘查开发院，内蒙古 赤峰024005；4.湖南省地质矿产勘查开发局四○九队，湖南 永州425000；)

地球化学元素的异常下限值确定是地球化学中重要的问题之一,目前还没有一个完善的具有科学依据的计算方法。传统的化探异常下限值计算是以元素含量或元素含量的对数值呈正态分布这一假设为基础的，而事实上地球化学元素含量的空间分布是极其复杂的。研究表明,地球化学景观可能是一个具有低维吸引子的混沌系统,元素的地球化学背景值和异常具有各自独立的幂指数关系,由此导致了一种多重分形分布,可以利用元素的分形分布求出其异常下限。对湖南省阳明山地区的化探水系采样分析数据采用分区的处理方法，根据每个区内数据的分布特征采用分形和传统方法混合应用来确定异常下限，勾绘出Sn元素异常图，与单独采用传统方法相对比收到了良好的异常圈定效果。根据新方法确定的元素异常下限所圈定的异常区与已知矿点高度拟合。

元素异常下限；含量-面积；MAPGIS；湖南省阳明山

0　引　言

地球化学异常一直是进行矿产预测的重要依据，地球化学异常下限的确定是圈定地球化学异常的重要工作之一，但迄今为止还没有找到一个合理计算地球化学异常下限的科学方法，在实际工作中要结合实际地质情况，在充分研究地质背景的基础上，合理地确定使用的计算方法[1]。传统的地球化学异常下限的确定主要是使用经典的统计学方法，以样品数据呈正态分布为假设前提，通过计算数据的统计学参数对异常下限进行确定，一般是以平均值(X)与n倍的标准离差之和作为地球化学异常下限值，即：T=X+nS0(其中T为异常下限值，X为平均值，S0为标准离差，n=1～3)。该方法仅适用于地球化学数据呈正态分布或对数正态分布的情况，但新的研究表明元素的地球化学分布并不局限于正态分布或对数正态分布[2-5]，非正态分布或非对数正态分布的元素数据具有不规则性和自相似性，李长江等1995年研究揭示的地球化学景观可能是一个具有低维(D=2.9)吸引的混沌系统，具有典型的分形特征[6]。多维分形模型不仅采用常规的低阶矩统计，而且采用高阶矩统计对多维分形分布进行度量，从而能较细致地刻画正常值以及异常值。地球化学元素的正常值不仅服从统计学中的大数定律，即满足正态分布或对数正态分布[7]，而且应该包括多重分形分布[8]。传统方法并不具备刻画异常值的功能[9-14]，惯用的统计方法只能描述地球化学元素围绕均值周围的变化规律[7]。通过多维分形理论不但能够清楚地反映出统计方法的这些局限性，而且能有效地克服统计方法的不足[6]。研究区内，受花岗岩体侵入的影响，岩体及岩体周围W、Sn元素含量高出外围1～2个数量级。若采用传统方法确定异常下限难以对研究区内的异常进行有效圈定，且会导致异常圈定范围过大以及研究区外围无异常的现象。为解决这一难题，本文以绘制湖南省阳明山地区Sn元素异常图为例，采用分子区方法，对岩体以及受岩体影响的周边区域采用分形方法确定异常下限，对研究区外围采用传统方法确定异常下限，成功进行了化探单元素异常的圈定。

1　研究区地质特征

研究区位于湖南省阳明山地区。区内以寒武系—奥陶系最发育，泥盆系—三叠系仅零星分布，二者呈角度不整合接触。工作区主体位于阳明山隆起区，为多组深大断裂的交汇部位。区内构造以阳明山—大义山东西向基底断隆带、阳明山—骑田岭北西向基底断隆带为主，其控岩、控矿作用最为明显，在区域上控制了阳明山复式岩体及铅锌钨锡多金属成矿带(图1)。区内经历了加里东期、印支期、燕山期、喜山期等多期复杂的构造运动，这些构造运动均属于区域性造山运动，伴随有强烈的岩浆活动。区内岩浆岩发育，具多期、多阶段特征。侵位时代以印支期为主，其次为燕山早期；成因类型为壳源重熔型(S型)。主要岩体为阳明山复式花岗岩，其次为花岗斑岩脉、细粒花岗岩脉、煌斑岩脉等。

2　分形模型及分维数求取

分形是其组成部分以某种方式与整体相似的形[15]。这一定义反映了自然界中很广泛的物质的基本属性:局部与局部、局部与整体在形态、结构、功能和信息等方面具有(统计意义上的)自相似性。定量描述这种自相似性的参数称为“分维数”或简称“分维”，记为D。许多地质现象具有标度不变的特征,如断层、地震、火山喷发和矿产等。这些现象的频度和大小之间的分布具有尺度不变性。分形分布的特点要求大于等于某一尺度的数目或和数，与物体大小之间存在幂函数关系，即

N(r)=Cr-D(r>0)

(1)

式中：r表示特征尺度；C>0，称为比例常数；D>0，称为分维数；N(r)=N(≥r)表示尺度大于等于r的数目或和数。

为了求出其分形模型中分维数，将观测数据(N(r1)，N(r2)，…，N(rn))和(r1，r2，…，rn)绘在双对数坐标纸上，如果其散点大致分布在一条直线上的话，其分维数D便可以利用直线的斜率求出。也就是将观测数据(N(r1)，N(r2)，…，N(rn))和(r1，r2，…，rn)代入N(r)=Cr-D式中，然后两边取对数，得lgN(r)=-Dlgr+lgC，用最小二乘法求出斜率D的估计量，即为分维数；如果其散点大致分布在两段直线上, 可以采用分段拟合，有的分界点清楚，有的则不清楚，为了提高分界点确定的客观性，在两个区间用最小二乘法进行回归时用最优化方法确定分界点。其基本思想是，找出合适的分界点ri，使各区间拟合的直线与原始数据之间的剩余平方和Ei(i=1，2)在两个区间的总和为最小。其中ri是分界点；D1和D2分别为区间的斜率，即分维数。

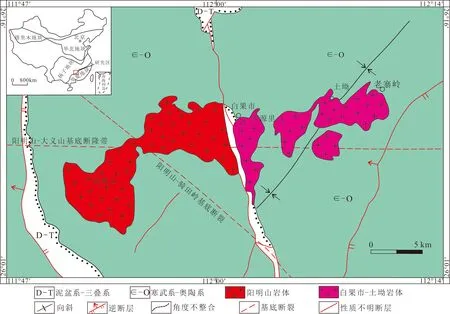
图1　研究区地质图(据湖南省地质矿产局四〇九队，2012*湖南省地质矿产局四〇九队.湖南阳明山地区矿产远景调查总体设计.2012.)Fig.1　The geological map of the study area

(2)

为了检验回归方程的显著性，应对每个回归方程进行相关系数检验及方差分析检验。分界点的地质意义可以看成元素含量在空间上至少存在两个层次的分布, 即小于分界点ri对应的值为元素含量的背景分布, 大于分界点ri对应的值为元素含量的异常分布，ri对应的值为元素含量分布的异常下限。Cheng等1994年从分形的观点认识到地球化学背景值和异常具有各自独立的幂指数关系, 由此导致了一种多重分形分布[10]。在此基础上,Cheng等1994年提出了确定地球化学异常的含量-面积分形方法[10]。地球化学元素含量-面积的分形分布服从如下方程：

C=kAa

(3)

其中：C为含量；k为常数；A为大于含量C的面积；a是与最大奇异指数有关的指数。

3　区域元素分布模型的建立

结合该区域地质演化历史、地层和岩体的分布特征及物化探资料分析，并且经水系沉积物样品测试分析可知，岩体内及接触带Sn元素含量较周围高出很多，于是建立简化的元素分布规律模型(图2)。该模型中A子区代表蚀变区，其Sn元素含量包括原地质体中Sn元素含量以及受岩体和热液影响叠加在原背景值上的元素含量的和。B子区为未蚀变区，其Sn元素含量仅代表地层沉积中的原始元素含量。岩体周围的蚀变矿化带是以水系沉积物样品分析测试出的数据为基本，并结合前人物化探资料加以确定，并进而在MAPGIS软件的空间分析子系统中，应用缓冲区分析功能，以距岩体2.5 km的距离绘出蚀变带范围[16]。

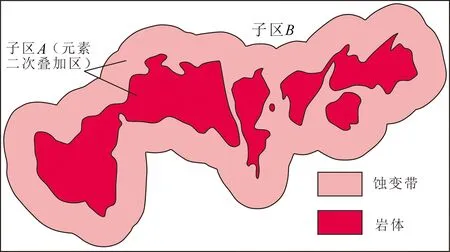
图2　研究区元素分布规律模型Fig.2　Distribution model of the elements in the study area

4　含量-面积法的MAPGIS实现流程及结果

4.1异常下限的确定

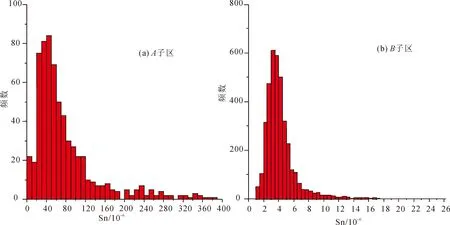
图4　Sn元素原始数据分布直方图Fig.4　The distribution histogram of Sn element data

地质学中的许多事物都具有复杂的空间属性，往往表现出非线性和不规则性。传统的方法忽略了元素含量的空间信息，仅强调元素含量值的频率分布。非线性理论和方法的提出，为揭示隐藏于混乱复杂现象中的精细结构和定量地刻画描述它们提供了理论方法基础。分形理论作为非线性科学的分支，在地球物理学和地质学中得到了广泛的应用。目前，利用分形理论进行地球化学异常下限确定的方法有：含量-面积法、周长-面积法、含量-个数法、含量-距离法、求和法等[17]。

地理信息系统即为GIS，是一种获取、存储、检索、操作、分析和显示地球空间数据的计算机系统。将GIS与分形统计学结合起来，在GIS平台上对地学图形和数学信息进行分析及统计处理，将会使原来比较繁杂的分形计算操作过程变得方便简捷，易于实现。MAPGIS是由武汉中地信息工程有限公司研制的一种属于矢量型的GIS软件。下面以MAPGIS软件为例, 说明在GIS系统中用含量-面积法确定化探异常的实现方法。

具体实现过程如图3所示。

图3　A子区确定异常下限的流程图Fig.3　Flow chart to determine the threshold of subarea A

(1)利用MAPGIS空间分析子系统进行点对区相交分析，提取出A子区内的元素数据点，形成点文件，称为A点文件。

(2)将A点文件的属性数据转成Excel格式(含元素分析数据值)，统计分析A子区内元素的异常下限值。经检验，A区不严格服从正态分布(图4(a))。

图5　A子区内大于确定的r值所形成的范围Fig.5　Area that is greater than the defined value r in subarea A

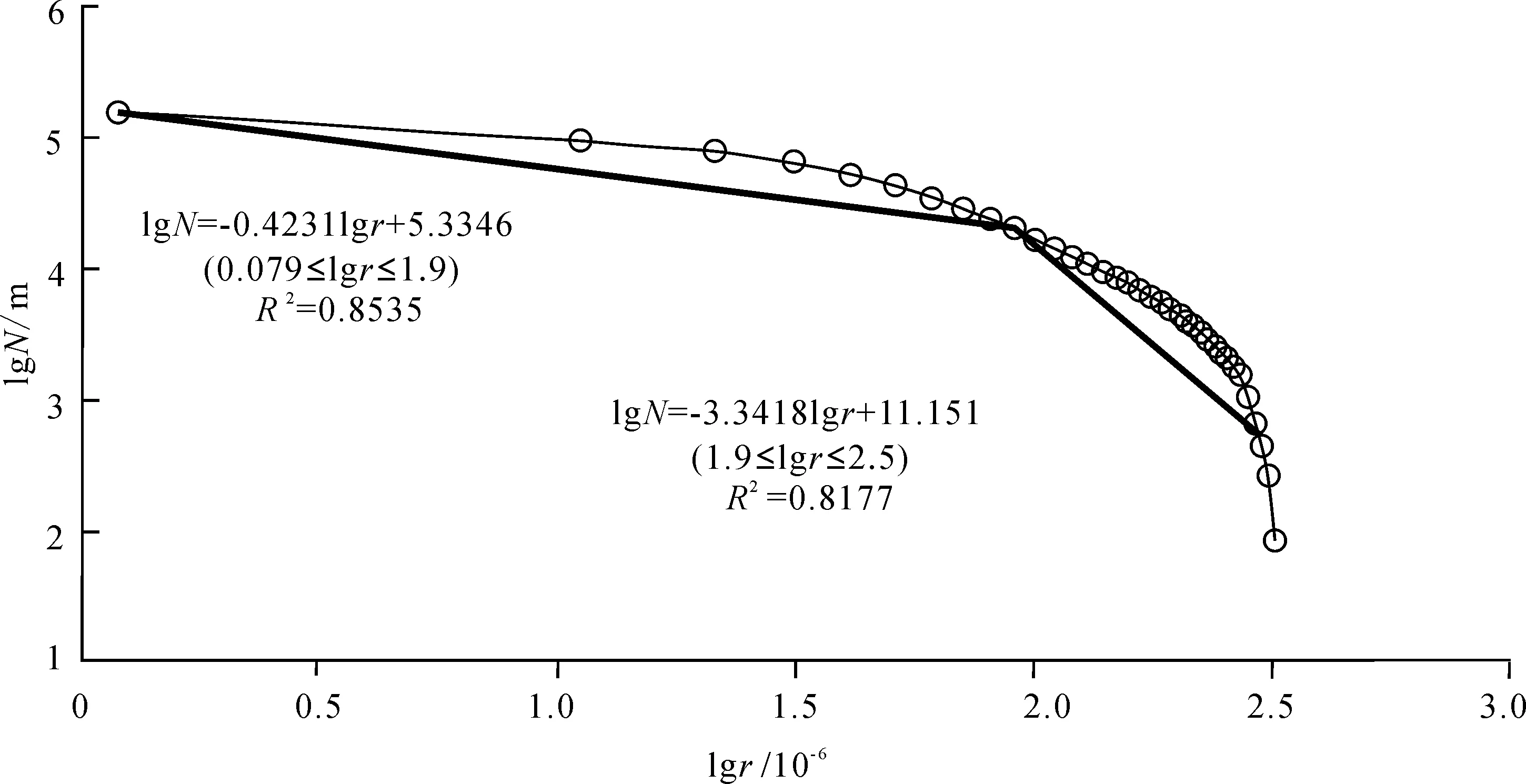
图6　A子区内Sn元素的含量-面积法分布直线拟合图Fig.6　The distribution linear fitting chart of Sn by content-area method in subarea A

(3)用分形方法，即含量-面积法确定异常下限。由于A区面积是不规则的，故在A区内用TIN(不规则三角网)方法，以Sn元素含量10×10-6为步长勾绘地球化学等值线图，由于绘出的图件比A区面积稍大，为了减少误差，故用A区与绘制出的等值线图的区文件在MAPGIS子系统中做区与区相交操作，然后在MAPGIS空间分析系统中进行含量—面积分形方法的相关操作[17-18](图5)。最后绘制出分形的拟合曲线，确定异常下限。研究区基于MAPGIS平台上对模型内A区的数据求得异常下限约为80×10-6(图6)。

(4)对模型内B子区原始数据进行特高值处理后，数据基本符合正态分布(图4(b))，采用传统方法进行异常下限计算。在Grapher软件中，采用公式即T=X+2S0统计计算，得到Sn异常下限为6×10-6。

4.2异常圈定结果

Sn元素异常及与已知矿点的拟合图如图7和图8所示。利用各子区内的所有数据值除以其各自异常下限得到相应的数据，然后将数据在MAPGIS投影变换子系统中投影成点文件。再在MAPGIS的DTM子系统中进行等值线图绘制，以1、2和4数值分别作为单元素异常的外带、中带和内带的边界值，则得到效果图(图7)。与单独采用传统方法统计算出的整个研究区异常下限绘出的图件(图8)相比较，分区分别确定异常下限绘出的图件效果明显较好，它既解决了模型中A区异常勾绘面积过大的问题，又准确地勾绘出了模型中B区内的异常范围。

图7　Sn元素异常图(含量-面积分形法)及与已知矿点的拟合(Sn含量单位为10-6)Fig.7　Sn anomaly map by content-area fractal method and fitting with the known ore spots

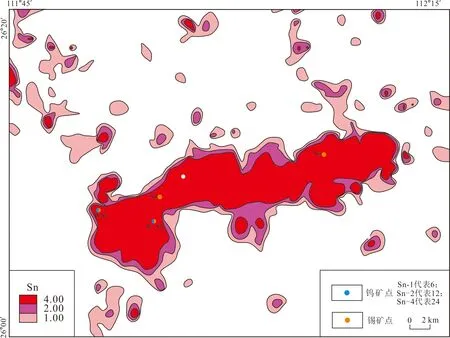
图8　Sn元素异常图(传统方法)及与已知矿点的拟合(Sn含量单位为10-6)Fig.8　Sn anomaly map by traditional method and fitting with the known ore spots

5　结　论

应用本文的模型划分子区，对A区范围内的锡元素数据应用分形方法确定异常下限，并对B区范围内的锡元素数据应用传统方法确定异常下限，较好地圈定了研究区内锡元素异常的有效范围，且与已知矿点得到很好的拟合，这一方法的成功实践对研究区下一步找矿勘探具有十分重要的指导意义。

[1]戴慧敏，宫传东，鲍庆中，等. 区域化探数据处理中几种异常下限确定方法的对比——以内蒙古查巴奇地区水系沉积物为例[J].物探与化探，2010，34(6)：782-786.

[2]李长江，麻土华.矿产勘查中的分形、混沌与ANN[M].北京：地质出版社，1999：1-140.

[3]谢淑云，鲍征宇. 多重分形与地球化学元素的分布规律[J].地质地球化学，2003，31(3)：97-102.

[4]ALLEGREC J,LWEIN E.Scaling laws and geochemical distributions[J].Earth and Planetary Science Letters, 1995, 132(1/4): 1-13.

[5]TURCOTTED L.A fractal approach to the relationship between ore grade and tonnage[J]. Economic Geology, 1986, 81 (6) : 1528-1532.

[6]李长江，麻土华，徐有浪，等. 地球化学景观吸引子的发现及其意义[J].浙江地质，1995，11(1)：86-90.

[7]成秋明.多维分形理论和地球化学元素分布规律[J].地球科学，2000，25(3)：311-318.

[8]蒙勇，牛件生，吕宇明，等. 广西贵港银山岭铅锌矿土壤地球化学找矿研究 [J]. 现代地质，2011，25(5)：1013-1020.

[9]AGTERBERGF P, CHENG Q M, WRIGHT D F. Fractal modeling of mineral deposits: applications of computers and operations research in the mineral industry[M]//ELBROND J, TANG X. Proc 24th APCOM Symposium (Montreal). Westmount Canadian: Institute of Mining, Metallurgy and Petroleum, 1993:43-53.

[10]CHENG Q M, AGTERBERG F P, BONHAM-CARTER G F. A spatialanalysis method for geochemical anomaly separation[J].Journal of Geochemical Exploration, 1996, 56(3): 183-195.

[11]CHENG Q M, AGTERBERG F P, BALLANTYNE S B. The separation of geochemical anomalies from background by fractal methods[J].Journal of Geochemical Exploration, 1994, 51(2): 109-130.

[12]CHENG Q M, BONHAM-CARTER G F, HALL G E M, et al. Statistical study of trace elements in the soluble organic and amorphous Fe-Mn phases of surficial sediments, Sudbury basin: 1. Multivariate and spatial analysis[J]. Journal of Geochemical Exploration, 1997, 59(1): 27-46.

[13]CHENG Q M. Multifractality and spatial statistics[J]. Computer & Geosciences, 1999, 25(9): 949-962.

[14]CHENG Q M. Gliding box method and multifractal modeling[J]. Computer & Geosciences, 1999, 25(9): 1073-1080.

[15]MANDELBROT B B.The Fractal Geometry of Nature[M].New York: W. H. Freeman and Company, 1982: 1-458.

[16]吴信才. MAPGIS地理信息系统[M]. 北京：电子工业出版社，2004：191-194 .

[17]申维. 分形混沌与矿产预测[M]. 北京：地质出版社，2002：1-94.

[18]李随民，姚书振.基于MAPGIS的分形方法确定化探异常[J].地球学报，2005，26(2)：187-190.

Determination of the Element Anomaly Threshold and the Enclosed Abnormal Area by Using Content-Area Fractal Method Based on MAPGIS：Exampled by Yangmingshan Area of Hunan Province

CUI Yuliang1,2, WANG Genhou2, LANG Xinxin3, ZENG Zhifang4

(1.Beijing Institute of Exploration Engineering，Beijing100083, China;2.School of Earth Sciences and Resources, China University ofGeosciences,Beijing100083,China;3.InnerMongoliaTenthGeologicalMineralExplorationInstitute,Chifeng,InnerMongolia024005,China;4.409Team,BureauofGeologyandMineralExplorationandDevelopmentofHunan,Yongzhou,Hunan425000,China)

The determination of thresholds of chemical elements is one of the important problems in geochemical exploration. At present, there is not a scientific way to confirm the thresholds.The traditional way to determine the thresholds of chemical elements is based on the assumption of normal distribution of the element contents or their logarithms. In fact,the space distribution of geochemical element content is extremely complex; and the studies showed that the geochemical landscape may be a low-dimensional chaotic attractor system. The background values and anomalies of the elements have their own exponential relationship, which lead to a multi-fractal distribution, thus obtaining the anomaly threshold of element through the distribution of fractal elements. In this paper, the method of dividing area of geochemical exploration sample analysis data in Yangmingshan in Hunan is adopted. The threshold is determined through mixed application of fractal and traditional methods according to the distribution of data，drawing out the Sn anomaly map. It obtained better performance than by using the traditional method only, and the abnormal area enclosed by the element anomaly thresholds which is determined by the new method highly conformed to the known ore spots.

element anomaly threshold; content-area; MAPGIS; Yanmingshan area of Hunan Province

2015-05-12；改回日期：2016-03-28；责任编辑：戚开静。

中国地质调查局项目(1212011220522)。

崔玉良，男，硕士研究生，1989年出生，构造地质学专业，主要从事构造地质学研究。Email：814399394@qq.com。

王根厚，男，教授，博士生导师，1963年出生，构造地质学专业，长期从事构造地质学的教学与科研工作。Email：wgh@cugb.edu.cn

P632

A

1000-8527(2016)04-0811-07