梁格法在连续斜交宽幅空心板桥承载力评定上的运用

■翁旭恒　李琳琳

（1.福建省交通科学技术研究所；2.福建省公路、水运工程重点实验室，福州　350004；3.湖北省交通规划设计院，武汉　430050）

梁格法在连续斜交宽幅空心板桥承载力评定上的运用

■翁旭恒1,2李琳琳3

（1.福建省交通科学技术研究所；2.福建省公路、水运工程重点实验室，福州350004；3.湖北省交通规划设计院，武汉430050）

在桥梁荷载试验检测评定桥梁的承载能力中，引入空间梁格对某连续斜交宽幅空心板桥进行等效模拟，建立该桥的空间梁格有限元计算模型，分析设计活载及试验荷载作用下上部梁体结构的静动载试验响应，并通过现场对该桥的静动载试验检测结果评定该桥的承载能力。结果表明，在试验荷载作用下梁体处于弹性范围之内，承载能力能满足设计荷载等级要求。

空间梁格斜交空心板桥有限元计算静动载试验承载能力评定

1　前言

由于受地形限制以及交通路网通行的要求，宽梁桥、斜交梁桥等受力复杂的结构形式不断涌现［1］。传统的梁单元模型和杆单元模型在荷载试验中运用具有一定的局限性，无法对桥梁的承载能力做出精确的分析评定。梁格法以其较为成熟的软件基础和较精确的结果分析，在斜交梁桥、宽梁桥得到广泛的运用。

1.1基本概念

空间梁格法的主要思路就是将桥梁上部结构用一个等效的梁格模拟，将分散在主梁每个区段内的弯曲刚度和抗扭刚度集中于最邻近的等效梁格内，实际结构的纵向刚度集中于纵向梁格构件内，而横向刚度则集中于横向梁格构件内。理论上，当原型实际结构和对应的等效梁格承受相同荷载时，两者的抗弯承载力应相等。

1.2梁格划分的基本原则

建立空间梁格模型时，要视上部结构断面形式的不同进行不同形式的梁格单元划分和截面特性计算，划分过程均需遵循等效性原则［2～3］。

汉勃利等人提出梁格模型梁格的划分应综合考虑以下因素：

（1）为了得到每条腹板各个截面的设计弯矩和设计剪力，在每条腹板处设置纵向单元。为了加载的方便，在悬臂端部设置虚拟的纵向单元。

（2）梁格的纵向杆件形心高度位置应尽量与箱梁截面的形心高度相一致，纵横杆件的中心与原结构梁肋的中心线相重合，使腹板剪力直接由所在位置的梁格构件承受。

（3）横向单元应与纵向单元垂直，一般在跨中、1/4跨、1/8跨、支座处，横格梁处设置横向单元。横向单元的间距直接决定了荷载在纵向单元之间的传递，间距过大会使相邻纵向单元间的力产生很大跳跃；间距太密又会大大增加工作量，也毫无必要。为保证荷载的正确传递，最大间距不能超过相邻两个反弯点间距的1/4，在支点的附近应适当加密。

（4）纵梁抗扭刚度的计算按整体箱形断面自由扭转刚度平摊到各纵梁上。

（5）预应力钢筋在梁肋中的布置应特别引以注意。对于整个箱梁截面而言，预应力钢筋是对称配置的。由于梁格划分后边肋几何形状的非对称性，此时按设计位置布置预应力钢束，在边肋中将产生较大的平面外弯矩，这显然与实际受力情况不符，在计算结果的分析中应扣除平面外弯矩产生的效应。

基于以上的梁格法理论原则，通过midas Civil有限元软件，对某连续斜交宽幅空心板桥进行静载试验理论计算，结合实测结果评定该桥的承载力。

2　工程实例

某高速立交桥中心桩号为GK18+833.712，采用4× 19.5m现浇全预应力混凝土连续空心板梁结构，斜交角度为66.847o。该桥分左右幅，单幅桥宽为16.5m（0.5m防撞护栏+15.5m机动车道+0.5m防撞护栏）。上部结构采用等高度预应力混凝土连续空心板梁，采用C50混凝土，梁高1.1m，顶板宽16.5m，底宽14.0m。下部构造采用三柱式桥墩，“一”字型桥台，摩擦桩基础。桥面铺装：4.5cm厚改性沥青混凝土+5.5cm厚中粒式沥青混凝土+6cm C40防水混凝土调平层。设计荷载：公路-I级。建造材料：混凝土，上部结构采用强度等级为C50混凝土，弹性模量Ec= 3.45×104MPa，重力密度γ=26.0kN/m3，泊松比μ=0.2，混凝土轴心抗压强度标准值fck=32.40MPa，抗拉强度标准值ftk=2.65MPa；纵向预应力钢束采用高强度低松弛钢绞线，松弛系数为0.3，标准强度fpk=1860MPa，张拉控制应力为0.72fpk=1340MPa，公称直径Φs15.2mm，弹性模量Ep=1.95× 105MPa。普通钢筋采用HPB300和HRB335钢筋。该桥平面、立面及跨中横断面图如图1、2、3所示。

3　有限元模型建立

3.1斜交宽板梁等效简化

根据梁格法纵向梁格划分原则，利用 midas Civil有限元分析软件建立该桥的计算模型，进行静载理论计算。全桥有限元梁格模型共建立了944个节点，1783个空间梁单元，其中928个纵向梁单元，855个横向联系单元。纵向梁格划分等效简化图及梁格法有限元模型如图4、图5所示。

3.2静载理论分析

通过将所有的横向联系梁定义为一个结构组，选择按“横向联系梁”的方法分布移动荷载。计算得到该桥在公路-I级设计活载作用下，截面最大正弯矩为537kN·m，最大剪力为392kN。在设计活载作用下，结构的内力包络图如图6所示。

3.3动载理论分析

对该桥进行特征值分析，计算结果表明，桥梁的基频为5.29Hz，对应振型为反对称竖弯，振型图如图7所示。

4　现场试验及结果分析

4.1试验项目

依据桥跨结构所得的活载内力包络图及外观检查结果，选择该桥跨左幅第1跨、第2跨进行试验，具体如表1所示，桥跨主要测试截面如图8所示。

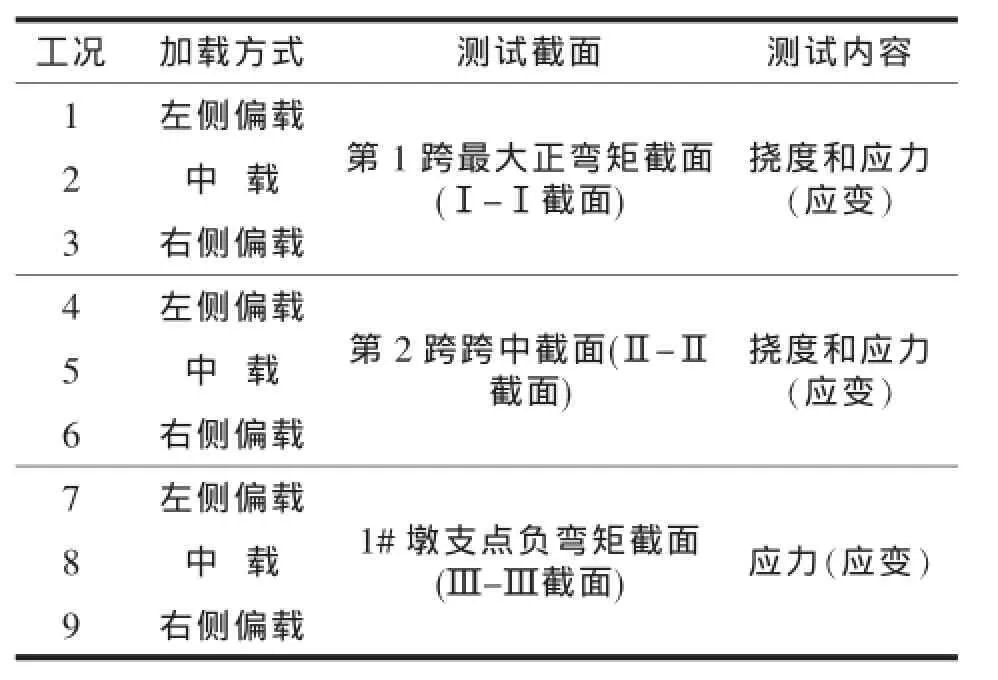
表1　　试验测试内容

在以上控制截面，每个截面梁底布置8处应变测点和3处挠度测点，左右侧腹板各2处应变测点。应变采用东华静载数据采集仪进行测试。

在第1跨、第2跨的支点、1/4L、2/4L、3/4L桥跨位置布置脉动测点，采用INV DASP动态测试与分析系统分析脉动信号。在第2跨跨中位置布置光电测点，采用光电挠度仪进行无障碍行车试验。

4.2静载试验及结果分析

本次试验以设计活载产生的该项目最不利效应值等效换算，确定需要4辆重约35t的车辆进行等效加载，分三级逐级递加到最大荷载，然后一次性卸载至零荷载状态。加载车辆布置如图9所示。该桥的静载试验荷载效率满足《公路桥梁荷载试验规程》（JTG/T J21-01-2015）基本荷载试验规定的要求［4］。

（1）挠度测试结果与分析

在各级试验荷载作用下，该桥各控制截面代表性测点荷载与挠度关系曲线如图10所示，挠度实测值与理论值比较如表2所示。

在试验工况荷载作用下，各控制截面控制测点荷载与挠度曲线基本保持线性关系，表明在试验荷载作用下梁体处于弹性范围之内。各测试截面挠度校验系数为0.50～0.71，相对残余挠度最大值为17.4%。

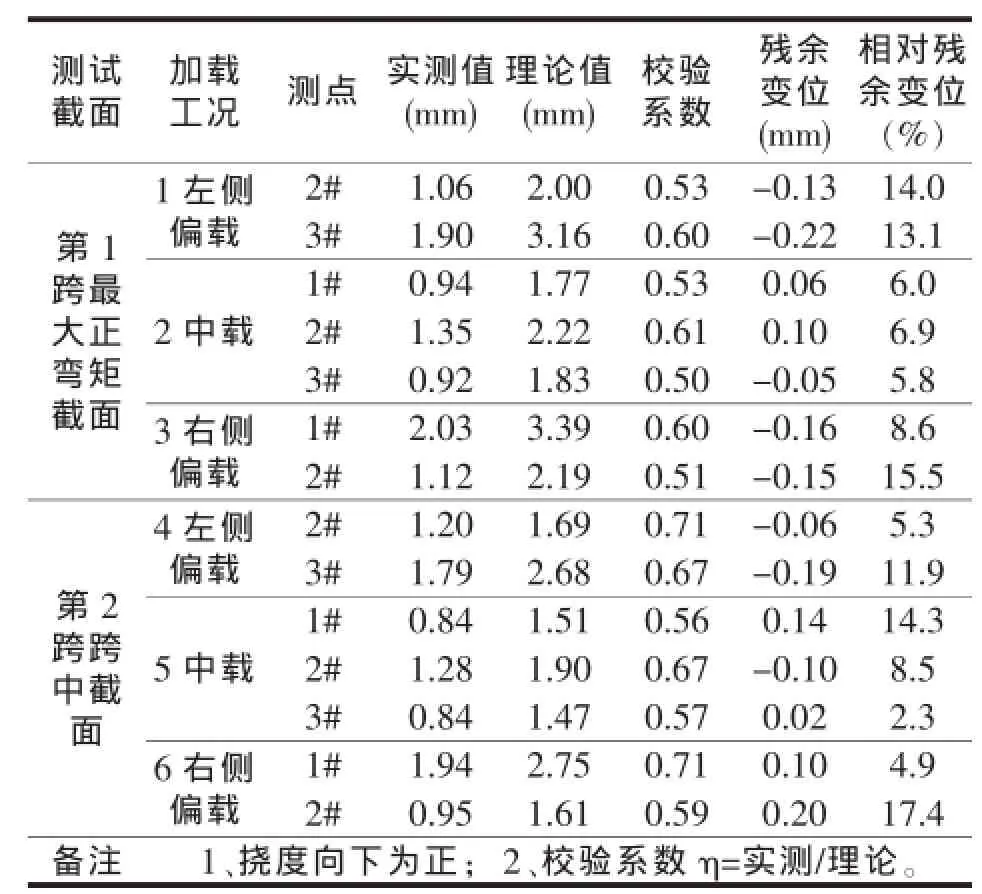
表2　各控制截面挠度分析表

（2）应变测试结果与分析

在各级试验荷载作用下，该桥各控制截面代表性测点荷载与应变关系曲线如图11所示，应变实测值与理论值比较如表3所示。

表3　各控制截面应变分析表

在分级荷载作用下，控制截面各控制测点荷载与应变基本保持线性关系，表明在试验荷载作用下梁体处于弹性范围之内。从表3可以看出，第1跨最大正弯矩截面应变校验系数为0.50～0.78，相对残余应变为0%；第2跨跨中截面应变校验系数为0.51～0.77，相对残余应变最大值为4.0%；1#墩支点负弯矩截面应变校验系数为0.50～0.67，相对残余应变最大值为14.3%。

各测试截面挠度和应变校验系数均小于或处于 《公路桥梁荷载试验规程》（JTG/T J21-01-2015）规定的常值范围（0.70～1.00），相对残余均小于《公路桥梁荷载试验规程》（JTG/T J21-01-2015）的规定限值（20%），结构接近于弹性工作状态。

4.3动载试验结果与分析

实测的信号经FFT分析、模态分析，得到该桥第2跨跨中测点时域波形图及频谱图如图12所示。经分析，该桥的实测一阶自振频率为6.45Hz，大于理论计算基频5.29Hz。在行车速度10km/h、20km/h、30km/h条件下，实测得第2跨跨中截面的跑车冲击系数分别为1.21、1.24、1.29，小于理论冲击系数1+μ的1.31。表明该桥的实际刚度较大，振动相应较小，行车性能较好，车辆对桥梁产生的冲击效应较小。

综上所述，采用梁格法计算的挠度、应变与实测的挠度、应变值较接近，试验校验系数、相对残余均满足规范要求，结构接近于弹性工作状态。同时，结合动载试验结果分析，实测数据普遍偏小，原因可能是未考虑桥面铺装对斜交板梁整体刚度的影响。

5　结论

梁格法是桥梁结构空间分析的一种有效方法。通过梁格法建模在本次连续斜交宽幅空心板桥承载力评定上的运用，可以得到如下结论：

（1）该桥的静载试验中，截面挠度和应变校验系数均满足规范要求，且横向变化趋势较吻合，说明梁格法能够较好的模拟斜交宽幅空心板梁的横向空间受力。

（2）该桥动载试验表明该桥的整体刚度较大，承载力较强，行车性能较好。

（3）该桥承载能力能满足公路-I级设计荷载等级要求。

（4）虽然梁格的等效性只能近似，但它能把握住结构的总体性能，在桥梁宽跨比较大的时候，能够较为精确的模拟桥梁的受力情况。建议在今后进行类似斜、弯、宽等异型板梁工程有限元模拟分析时，适当考虑桥面铺装对桥梁整体刚度的影响，可通过适当增加梁体顶板厚度并且桥面铺装层的恒载转换为质量作用在主梁上实现，以求有限元模型更加切合实际。

［1］范立础.桥梁工程（上）.北京：人民交通出版社，2000.

［2］E.C.汉勃力［英］.郭文辉译.桥梁上部结构性能［M］.北京：人民交通出版社，1982.

［3］戴公连，李德建.桥梁结构空间分析设计方法与应用［M］.北京：人民交通出版社，2001.

［4］JTG/T J21-01-2015，公路桥梁荷载试验规程［S］.北京：人民交通出版社，2016.