从《平行与垂直》片断谈新教师的课堂教学处理问题

田兴

近日，笔者听了校内新教师的教研课，课题是人教版教材四年级上册《平行与垂直》，觉得新教师在课堂教学处理方面确实有几个问题需要引起重视。我把其中的几个片断实录整理如下。

片断1：新授环节

师：根据大家的充分想象，我们整理了在同一平面上两根小棒的位置关系大致有以下几种样子。

师：想一想，给这些情况分分类，说说你是怎么想的？把分得的序号写在纸上。（以下是师生交流，教师把学生的分类情况进行板书，带括号部分是学生“个性化”的解释）

生1：1、8（竖横）。

6、9（像梯形的）。

4、5（是分开两条线）。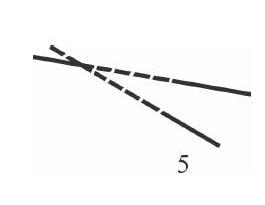

2、3（有角的）。

7（有交叉）。

生2：1、4、5、8、9（不连在一起）。

2、3、6、7（连在一起）。

生3：1、8（平平的）。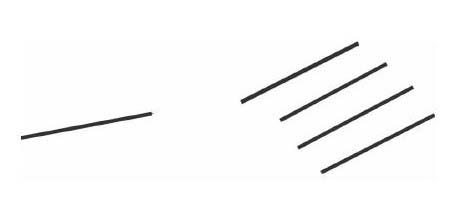

2、4、5（没有交叉的）。

3（有直角的）。

7（交叉）。

6、9（像梯子）。

（还有一些举手的学生，教师不再请学生回答了）

师：如果这两根小棒是孙悟空的金箍棒，谁来说金箍棒有什么特征呀？

生：会变长变粗，会无限延长。

师：谁能上来给这些直线延长。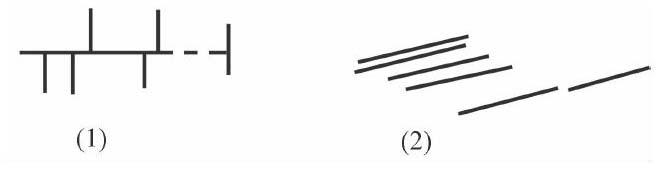

生：我来延长5。

生：我来延长4。

生：我来延长2。

生：我来延长3。

……

（继续请学生作其他几组直线的延长线）

师：请大家思考一下，现在我们的分类是不是应该变一下了？

生：4、5、7分为一类，它们都是会相交的，其他的分为一类。

生：1、8不会相交，1、3、4、5、6、7、9相交的。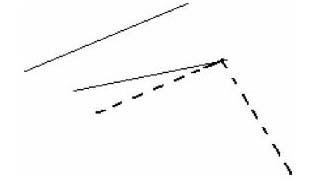

师：1、8会不会碰到一起呢？为什么？

生：它们都是直直的，延长后不会相交。

师：我们给这种情况取个名字？

生：平行。

（教师随即把前面3种分类从板书中擦除）

点评：请学生按照一定的标准对9种不同的情况进行分类，很好地体现了自主探究的思想，发挥了学生的主观能动性。但是当学生的发言出现了太多个性色彩的时候，教师不知道该怎么办了，所以只好重走旧路，返回来回想直线的特征，给每一组直线作延长线，以此来表明我们必须有一种新的分类，一种正确的分类。到此，我们发现了影响新教师课堂教学处理的一个重要因素——案教。当学生的思路不能纳入教师的预设，我们是为因势利导作有效点拨呢？还是为回归教案而重新开始？答案肯定是前者。课堂的时效性决定了教师不能做过多重复的教学行为，而是需要从学生的发言中寻找可利用因素，把握教学契机。以上案例，教学引导是到位的，但顺势引导出了问题，那么，如何针对3位学生的发言进行顺势引导呢？操作办法主要是对这3种分类进行讨论，而不是避而不谈。

方案1：

针对生2的连在一起与不连在一起的分类，教师可作这样的顺势引导：

师：这位同学说把1、4、5、8、9分为一类，那么这一类里还可以继续分类吗？

（教师意在引导学生把1、8先分离出来，并讲出1、8是永远不会相交的，而4、5、9是延长后会相交的，再后来把这种延长后会相交的和一看就连在一起的分到同一类中去，形成新的分类：相交）1、8和2、3、4、5、6、7、9

方案2：

针对生1的个性化分类，教师可做适当的整合。如可以引导学生讨论：

师：根据直线的特征，6、9会不会交叉？那4、5？2、3？7呢？

（学生把6、9独立出来，也有一定的好处，它可以方便下面相交以后的分类：分成一般相交和垂直相交）

方案3：

针对生3的分类，教师可引导学生进行讨论：

师：这位同学说2、4、5没有交叉，这种没有交叉与1、8一类有什么不同？（旨在引导学生通过对比分析平行与相交）根据直线的特征，哪些是始终不会相交的，哪些延长后会相交？

本案启示：作为新教师，正确处理好引导与顺势引导的关系非常重要，这种教学处理当然需要一定的智慧与能力，但最基本的前提还是在脑子里储备好这种意识。

片断2：巩固环节

师：到现在为止，我们已经学习了平行与垂直的有关知识。学得好不好，通过下面的贴小棒的活动就知道了。（每位学生手上都有两根小棒）现在，我在上面置一根小棒，请同学们再来贴一根，要求与这根小棒平行。

师呈现：请大家上来再贴一贴小棒，要求与这根小棒垂直。

（教师小结，课完）

点评：新教师对于教学资源的利用和充分利用这对关系时常不容易把握，有的是利用过度，有的是利用不到位。在这个环节，应该说贴平行与垂直的小棒这个设计是比较好的，它可以考查学生对于平行与垂直知识的掌握情况，但这个教学素材并没有被充分利用和展开，而只像走马观花式地过了堂。这里固然有学生思维单调的因素，但这和教师的教学引导也是分不开的。那么这个环节该怎么操作呢？其实只要做适当的引导，增加一定的变式练习即可：在学生贴平行与垂直时，要求他们尽量贴得与众不同而显得有创意。相信在不断的鼓励中，对于垂直，贴出（1）这样的效果应该是有可能的，贴出（2）这样的平行效果也不会很难。

贴了以后还要请学生说说为什么可以这样贴？怎么证明它们是平行的或垂直的？这样的练习设计拓展了思维的空间，为帮助学生理解平行与垂直的概念建立了一种较为科学的表象。为加深学生对概念的更深入的理解，我们可以设问：通过刚才的操作我们可以想象，如果画已知直线的平行线（垂线）可以画几条？（渗透无限思想）这些被画出来的直线彼此之间又有什么联系？（渗透平行线的传递性）为增进对平行与垂直这两者关系的理解，我们可以增加一个环节，演示两条直线从“一般相交—平行—垂直相交—一般相交—垂直”相交这样一种循环往复的过程，以此来揭示在同一平面内，两条直线的位置关系只有两种情况，不是平行就是相交。如下图示，如学生还表示怀疑，则可请学生举反例。

本案启示：如果把教学设想搞复杂一些，那么我们的教学操作就会显得简单一些。上好一节数学课，我们不仅要关注好的教学点子，更要关注如何把基础知识（基本能力）进行有效的落实。

综上两个片断分析，我们认为，新教师要进行有效的教学处理，必须以先进的理念做向导，继而进行教学手段的锤炼。我们的目标是努力使数学课体现出应有的厚度与深度。